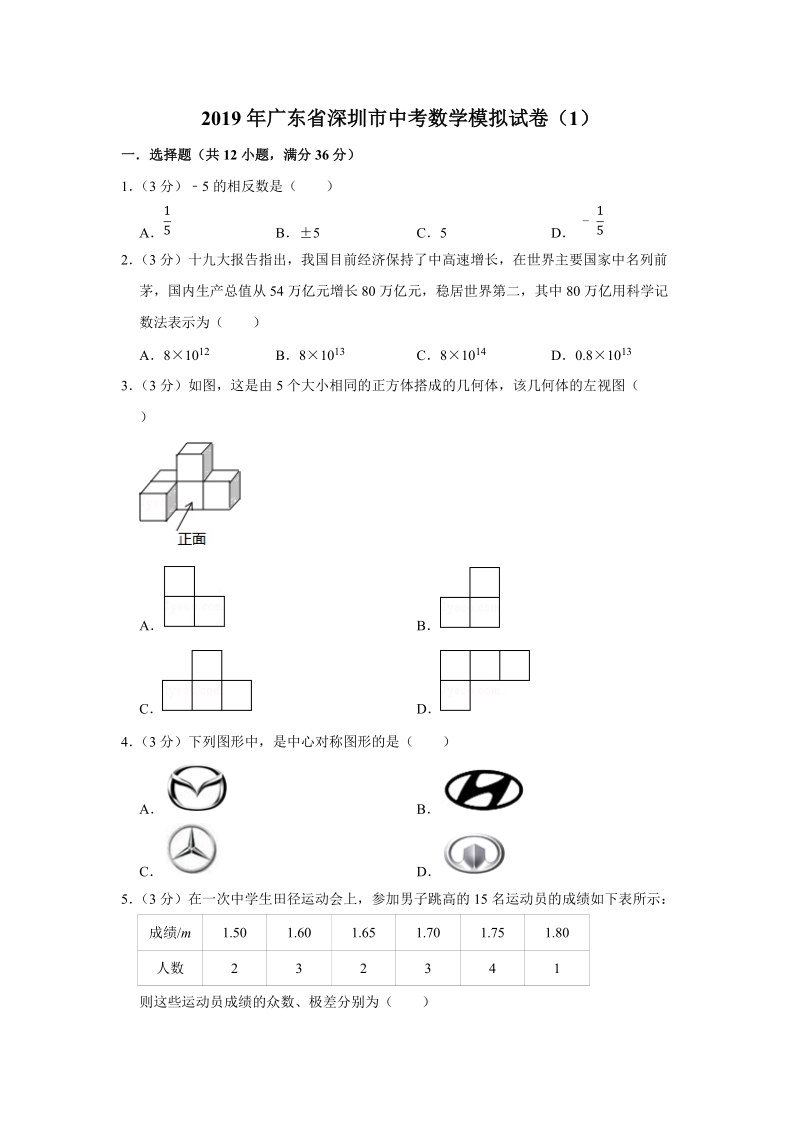
1、2019 年广东省深圳市中考数学模拟试卷（1）一选择题（共 12 小题，满分 36 分）1 （3 分）5 的相反数是（ ）A B5 C5 D15 -152 （3 分）十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从 54 万亿元增长 80 万亿元，稳居世界第二，其中 80 万亿用科学记数法表示为（ ）A810 12 B810 13 C810 14 D0.810 133 （3 分）如图，这是由 5 个大小相同的正方体搭成的几何体，该几何体的左视图（ ）A BC D4 （3 分）下列图形中，是中心对称图形的是（ ）A BC D5 （3 分）在一次中学生田径运动
2、会上，参加男子跳高的 15 名运动员的成绩如下表所示：成绩/m 1.50 1.60 1.65 1.70 1.75 1.80人数 2 3 2 3 4 1则这些运动员成绩的众数、极差分别为（ ）A1.70、0.25 B1.75、3 C1.75、0.30 D1.70、36 （3 分）下列各式计算正确的是（ ）Aa 3+2a23a 5 B3 4 7a+ a= aC （a 6） 2（a 4） 30 D （a 3） 2a4a 97 （3 分）如果一次函数 y2x4 的图象与另一个一次函数 y1 的图象关于 y 轴对称，那么函数 y1 的图象与 x 轴的交点坐标是（ ）A （2，0） B （2，0） C （
3、0，4） D （0，4）8 （3 分）如图，将直尺与含 30角的三角尺摆放在一起，若120，则2 的度数是（ ）A30 B40 C50 D609 （3 分） 九章算术是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响，该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出 8 元，多 3 元；每人出 7 元，少 4 元，问有多少人？该物品价几何？设有 x 人，物品价值 y 元，则所列方程组正确的是（ ）A B8y+3=x74= 8x+3=y74=C D8x-3=y7+4= 8y-3=x7+4=10 （3 分）如图，AB 是O 的直径，点 C 为 O 外一点， CA、CD
4、 是 O 的切线，A、D为切点，连接 BD、AD若 ACD48，则DBA 的大小是（ ）A32 B48 C60 D6611 （3 分）如图所示，抛物线 yax 2+bx+c 的顶点为 B（1，3） ，与 x 轴的交点 A 在点（3，0）和（2，0）之间，以下结论：b2 4ac0，2ab0 ， a+b+c0；ca 3，其中正确的有（ ）个A1 B2 C3 D412 （3 分）如图，四边形 OABC 是平行四边形，对角线 OB 在 y 轴上，位于第一象限的点A 和第二象限的点 C 分别在双曲线 y 和 y 的一支上，分别过点 A，C 作 x 轴的=1 =2垂线垂足分别为 M 和 N，则有以下的结论
5、：ONOM；OMAONC；阴影部分面积是 （ k1+k2） ；四边形 OABC 是菱形，则图中曲线关于 y 轴对称其中正确的12结论是（ ）A B C D二填空题（共 4 小题，满分 12 分，每小题 3 分）13 （3 分）因式分解：m 2 4n2 14 （3 分）张老师上班途中要经过 1 个十字路口，十字路口红灯亮 30 秒、黄灯亮 5 秒、绿灯亮 25 秒，张老师希望上班经过路口是绿灯，但实际上这样的机会是 15 （3 分）如图，在 RtABC 中，C90，AC5，以 AB 为一边向三角形外作正方形 ABEF，正方形的中心为 O，OC4 ，则 BC 边的长为 216 （3 分）如图，六边
6、形 ABCDEF 中，ABDE 且 AB DE，BC EF 且BCEF ，AFCD 且 AFCD，ABC DEF 120，AFEBCD90，AB2，BC1 ，CD ，则该六边形 ABCDEF 的面积是 = 3三解答题（共 7 小题，满分 0 分）17计算：（ ） 2 （ 4） 0 cos4512 - 9+ 3 - 218先化简代数式 1 ，并从1，0，1，3 中选取一个合适的代入求值-1212+219随着移动终端设备的升级换代，手机已经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况（选项：（A）和同学亲友聊天；（B）学习；（C）购物；（D）游戏；（E）其它） ，端午节后某中学
7、在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：选项 频数 频率A 10 mB n 0.2C 5 0.1D p 0.4E 5 0.1根据以上信息解答下列问题：（1）m ，n ，p （2）求本次参与调查的总人数，并补全条形统计图（3）若该中学约有 800 名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调查结果，就中学生如何合理使用手机给出你的一条建议20 （1）已知角 a 和线段 c 如图所示，求作等腰三角形 ABC，使其底角Ba，腰长AB c，要求仅用直尺和圆规作图，并保留作图痕迹 （不写作法）（2）若 a45，c2，求此三角形 ABC 的面积21
8、某服装店用 4000 元购进一批某品牌的文化衫若干件，很快售完，该店又用 6300 元钱购进第二批这种文化衫，所进的件数比第一批多 40%，每件文化衫的进价比第一批每件文化衫的进价多 10 元，请解答下列问题：（1）求购进的第一批文化衫的件数；（2）为了取信于顾客，在这两批文化衫的销售中，售价保持了一致若售完这两批文化衫服装店的总利润不少于 4100 元钱，那么服装店销售该品牌文化衫每件的最低售价是多少元？22如图，在 RtABC 中，C90，AD 平分BAC 交 BC 于点 D，O 为 AB 上一点，经过点 A，D 的O 分别交 AB，AC 于点 E，F，连接 OF 交 AD 于点 G（1）
9、求证：BC 是O 的切线；（2）设 ABx，AFy，试用含 x，y 的代数式表示线段 AD 的长；（3）若 BE8，sinB ，求 DG 的长，=51323如图，已知抛物线的顶点为 A（1，4） ，抛物线与 y 轴交于点 B（0，3） ，与 x 轴交于C，D 两点点 P 是 x 轴上的一个动点（1）求此抛物线的解析式；（2）当 PA+PB 的值最小时，求点 P 的坐标；（3）抛物线上是否存在一点 Q（Q 与 B 不重合） ，使CDQ 的面积等于BCD 的面积？若存在，直接写出点 Q 的坐标；若不存在，请说明理由2019 年广东省深圳市中考数学模拟试卷（1）参考答案与试题解析一选择题（共 12
10、小题，满分 36 分）1 （3 分）5 的相反数是（ ）A B5 C5 D15 -15【分析】利用相反数的概念：只有符号不同的两个数叫做互为相反数，进而得出答案【解答】解：5 的相反数是：5故选：C2 （3 分）十九大报告指出，我国目前经济保持了中高速增长，在世界主要国家中名列前茅，国内生产总值从 54 万亿元增长 80 万亿元，稳居世界第二，其中 80 万亿用科学记数法表示为（ ）A810 12 B810 13 C810 14 D0.810 13【分析】科学记数法的表示形式为 a10n 的形式，其中 1|a| 10，n 为整数确定 n的值时，要看把原数变成 a 时，小数点移动了多少位，n 的
11、绝对值与小数点移动的位数相同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数【解答】解：80 万亿用科学记数法表示为 81013故选：B3 （3 分）如图，这是由 5 个大小相同的正方体搭成的几何体，该几何体的左视图（ ）A BC D【分析】找到从几何体的左边看所得到的图形即可【解答】解：左视图有 2 列，每列小正方形数目分别为 2，1故选：A4 （3 分）下列图形中，是中心对称图形的是（ ）A BC D【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解【解答】解：A、不是中心对称图形，是轴对称图形，故本选项错误；B、是中心对称图形，不是轴对称图形，故本选项正确
12、；C、不是中心对称图形，是轴对称图形，故本选项错误；D、不是中心对称图形，是轴对称图形，故本选项错误故选：B5 （3 分）在一次中学生田径运动会上，参加男子跳高的 15 名运动员的成绩如下表所示：成绩/m 1.50 1.60 1.65 1.70 1.75 1.80人数 2 3 2 3 4 1则这些运动员成绩的众数、极差分别为（ ）A1.70、0.25 B1.75、3 C1.75、0.30 D1.70、3【分析】根据众数和极差的定义分别进行解答即可【解答】解：这组数据中 1.75m 出现次数最多，有 4 次，这组数据的众数为 1.75m，最大数据为 1.80m、最小数据为 1.50m，极差为 1
13、.801.500.30，故选：C6 （3 分）下列各式计算正确的是（ ）Aa 3+2a23a 5 B3 4 7a+ a= aC （a 6） 2（a 4） 30 D （a 3） 2a4a 9【分析】结合选项分别进行合并同类项、二次根式的加法运算、同底数幂的除法、积的乘方和幂的乘方等运算，然后选择正确答案【解答】解：A、a 3 和 2a2 不是同类项，不能合并，故本选项错误；B、3 4 7 ，计算正确，故本选项正确；a+ a= aC、 （a 6） 2（a 4） 31，原式计算错误，故本选项错误；D、 （a 3） 2a4a 10，原式计算错误，故本选项错误故选：B7 （3 分）如果一次函数 y2x4
14、 的图象与另一个一次函数 y1 的图象关于 y 轴对称，那么函数 y1 的图象与 x 轴的交点坐标是（ ）A （2，0） B （2，0） C （0，4） D （0，4）【分析】先根据两直线关于 y 轴对称的特点求出次函数 ykx +b 的解析式，再根据 x 轴上点的坐标特点求出一次函数的图象与 x 轴交点的坐标即可【解答】解：一次函数 ykx+b 的图象与直线 y2x 4 关于 y 轴对称，k2，b4，一次函数的解析式为：y2x4，当 y0 时，x 2，这个一次函数的图象与 x 轴交点的坐标为（2，0） 故选：B8 （3 分）如图，将直尺与含 30角的三角尺摆放在一起，若120，则2 的度数是
15、（ ）A30 B40 C50 D60【分析】先根据三角形外角的性质求出BEF 的度数，再根据平行线的性质得到2 的度数【解答】解：如图，BEF 是AEF 的外角，120，F30，BEF 1+F50，ABCD，2BEF50，故选：C9 （3 分） 九章算术是中国古代第一部数学专著，它对我国古代后世的数学家产生了深远的影响，该书中记载了一个问题，大意是：有几个人一起去买一件物品，每人出 8 元，多 3 元；每人出 7 元，少 4 元，问有多少人？该物品价几何？设有 x 人，物品价值 y 元，则所列方程组正确的是（ ）A B8y+3=x74= 8x+3=y74=C D8x-3=y7+4= 8y-3=
16、x7+4=【分析】根据题意可得等量关系：人数83物品价值；人数7+4物品价值，根据等量关系列出方程组即可【解答】解：设有 x 人，物品价值 y 元，由题意得：，8x-3=y7+4=故选：C10 （3 分）如图，AB 是O 的直径，点 C 为 O 外一点， CA、CD 是 O 的切线，A、D为切点，连接 BD、AD若 ACD48，则DBA 的大小是（ ）A32 B48 C60 D66【分析】根据切线长定理可知 CACD，求出CAD，再证明DBACAD 即可解决问题【解答】解：CA、CD 是O 的切线，CACD，ACD48，CADCDA66，CAAB，AB 是直径，ADBCAB90，DBA+DAB
17、 90，CAD+DAB90，DBACAD66，故选：D11 （3 分）如图所示，抛物线 yax 2+bx+c 的顶点为 B（1，3） ，与 x 轴的交点 A 在点（3，0）和（2，0）之间，以下结论：b2 4ac0，2ab0 ， a+b+c0；ca 3，其中正确的有（ ）个A1 B2 C3 D4【分析】根据抛物线的图象与性质即可判断【解答】解：抛物线与 x 轴有两个交点，0，b 24ac0，故 错误；由于对称轴为 x1，x3 与 x1 关于 x 1 对称，x3 时，y 0，x1 时，ya+b+ c0，故正确；对称轴为 x 1，= -2=2ab0，故正确；顶点为 B（1，3） ，yab+c 3，
18、ya2a+c 3，即 ca3，故 正确；故选：C12 （3 分）如图，四边形 OABC 是平行四边形，对角线 OB 在 y 轴上，位于第一象限的点A 和第二象限的点 C 分别在双曲线 y 和 y 的一支上，分别过点 A，C 作 x 轴的=1 =2垂线垂足分别为 M 和 N，则有以下的结论：ONOM；OMAONC；阴影部分面积是 （ k1+k2） ；四边形 OABC 是菱形，则图中曲线关于 y 轴对称其中正确的12结论是（ ）A B C D【分析】先判断出 CEON， ADOM，再判断出 CEAD，即可判断出正确；由于四边形 OABC 是平行四边形，所以 OA 不一定等于 OC，即可得出错误；先
19、求出三角形 COM 的面积，再求出三角形 AOM 的面积求和即可判断出 错误，根据菱形的性质判断出 OBAC，OB 与 AC 互相平分即可得出正确【解答】解：如图，过点 A 作 ADy 轴于 D，过点 C 作 CEy 轴 E，AMx 轴，CMx 轴，OBMN，四边形 ONCE 和四边形 OMAD 是矩形，ONCE，OMAD，OB 是OABC 的对角线，BOCOBA，S BOC S OBA ，S BOC OBCE，S BOA OBAD，=12 =12CEAD，ONOM，故正确；在 Rt CON 和 RtAOM 中，ONOM，四边形 OABC 是平行四边形，OA 与 OC 不一定相等，CON 与A
20、OM 不一定全等，故 错误；第二象限的点 C 在双曲线 y 上，=1S CON |k1| k1，=12 = -12第一象限的点 A 在双曲线 y 上，=2SAOM |k2| k2，=12 =12S 阴影 S CON +SAOM k1 k2 （k 2k 1） ，= -12 +12 =12故错误；四边形 OABC 是菱形，ACOB，AC 与 OB 互相平分，点 A 和点 C 的纵坐标相等，点 A 与点 C 的横坐标互为相反数，点 A 与点 C 关于 y 轴对称，故 正确，正确的有 ，故选：D二填空题（共 4 小题，满分 12 分，每小题 3 分）13 （3 分）因式分解：m 2 4n2 （m +2
21、n） （m 2n） 【分析】先将所给多项式变形为 m2（2n） 2，然后套用公式 a2b 2（a+b） （ab） ，再进一步分解因式【解答】解：m 24n 2，m 2（2n） 2，（m+2n） （m2n） 14 （3 分）张老师上班途中要经过 1 个十字路口，十字路口红灯亮 30 秒、黄灯亮 5 秒、绿灯亮 25 秒，张老师希望上班经过路口是绿灯，但实际上这样的机会是 512【分析】根据题意和概率的知识，可以求得张老师上班经过路口是绿灯的机会，本题得以解决【解答】解：张老师上班经过路口是绿灯的机会是： ，2530+5+25=2560=512故答案为： 51215 （3 分）如图，在 RtABC
22、 中，C90，AC5，以 AB 为一边向三角形外作正方形 ABEF，正方形的中心为 O，OC4 ，则 BC 边的长为 3 2【分析】作 EQx 轴，以 C 为坐标原点建立直角坐标系，CB 为 x 轴，CA 为 y 轴，则A（0，5） 设 B（x ，0） ，由于 O 点为以 AB 一边向三角形外作正方形 ABEF 的中心，利用 AAS 得到三角形 ABC 与三角形 BEQ 全等，利用全等三角形的对应边相等得到ACBQ5，BCEQ，设 BCEQ x ，由 OM 为梯形 ACQE 的中位线，利用梯形中位线定理表示出 OM，再由 CM，表示出 O 坐标，进而表示出 OC 的长，根据已知 OC 的长列出
23、关于 x 的方程，求出方程的解得到 x 的值，即可确定出 BC 的长【解答】解：作 EQx 轴，以 C 为坐标原点建立直角坐标系，CB 为 x 轴，CA 为 y 轴，则 A（0，5） 设 B（x ，0） ，由于 O 点为以 AB 一边向三角形外作正方形 ABEF 的中心，ABBE，ABE 90，ACB90，BAC+ ABC90，ABC+ EBQ 90，BACEBQ，在ABC 和BEQ 中， ACB= BQE=90= ACBBQE（AAS） ，ACBQ5，BCEQ，设 BCEQx ，O 为 AE 中点，OM 为梯形 ACQE 的中位线，OM ，=5+2又CM CQ ，=12 =5+2O 点坐标为
24、（ ， ） ，5+2 5+2根据题意得：OC4 ，2=(5+2)2+(5+2)2解得：x3，则 BC3故答案为：316 （3 分）如图，六边形 ABCDEF 中，ABDE 且 AB DE，BC EF 且BCEF ，AFCD 且 AFCD，ABC DEF 120，AFEBCD90，AB 2，BC1 ，CD ，则该六边形 ABCDEF 的面积是 = 3 33【分析】连接 AE，BD ，则AFEDCB，故六边形 ABCDEF 面积为 2SBCD +S 四边形ABDE分别计算其面积即可解题【解答】解：连接 AE，BD ，作 AGDE，由题意知AFEDCB，AEBD ，且六边形 ABCDEF 面积为 2
25、SBCD +S 四边形 ABDEAF ，FE1，= 3FEA 60，且 AE 2，= 2+2=DEF120，AEG60，AG 2 ，=32 = 3平行四边形 AEDB 的面积为 DEAG2 2 3= 3S BCD 1 ，=12 3=32六边形 ABCDEF 面积为 2SBCD +S 四边形 ABDE2 2 3 32+ 3= 3故答案为 33三解答题（共 7 小题，满分 0 分）17计算：（ ） 2 （ 4） 0 cos4512 - 9+ 3 - 2【分析】直接利用零指数幂的性质以及特殊角的三角函数值和负指数幂的性质分别化简得出答案【解答】解：原式43+1 - 22221118先化简代数式 1
26、，并从1，0，1，3 中选取一个合适的代入求值-1212+2【分析】根据分式的混合运算法则把原式化简，根据分式有意义的条件确定 x 的值，代入计算即可【解答】解：原式1 -1 (+2)(+1)(1)1 -+2+1=+1+1+2+1，= -1+1由题意得，x1，0，1，当 x3 时，原式 = -1419随着移动终端设备的升级换代，手机已经成为我们生活中不可缺少的一部分，为了解中学生在假期使用手机的情况（选项：（A）和同学亲友聊天；（B）学习；（C）购物；（D）游戏；（E）其它） ，端午节后某中学在全校范围内随机抽取了若干名学生进行调查，得到如下图表（部分信息未给出）：选项 频数 频率A 10 m
27、B n 0.2C 5 0.1D p 0.4E 5 0.1根据以上信息解答下列问题：（1）m 0.2 ，n 10 ，p 20 （2）求本次参与调查的总人数，并补全条形统计图（3）若该中学约有 800 名学生，估计全校学生中利用手机购物或玩游戏的共有多少人？并根据以上调查结果，就中学生如何合理使用手机给出你的一条建议【分析】 （1）先根据 C 选项频数和频率求出总人数，再根据频率频数总数分别求解可得；（2）根据表格中数据即可补全条形图；（3）总人数乘以样本中 D、 E 的频率之和即可得【解答】解：（1）因为调查的总人数为 50.150（人） ，所以 m10500.2，n50 0.210，p500.
28、420，故答案为：0.2、10、20（2）由（1）知总人数为 50 人，补全图形如下：（3）800（0.1+0.4）400（人） ，建议：学生在假期里应该更加规范自己使用手机的情况，可以用于学习或其他有意义的事情20 （1）已知角 a 和线段 c 如图所示，求作等腰三角形 ABC，使其底角Ba，腰长AB c，要求仅用直尺和圆规作图，并保留作图痕迹 （不写作法）（2）若 a45，c2，求此三角形 ABC 的面积【分析】 （1）可先作出 2 的补角，即为等腰三角形的顶角，进而作出腰，在腰的同侧作出顶角，在顶角的另一边截取腰长，连接 BC 即可；（2）易得此三角形为等腰直角三角形，腰长为 2，利用面
29、积公式可得三角形的面积【解答】解：（1） ；（2）a45，c2，CB45，A90，三角形 ABC 的面积为 2221221某服装店用 4000 元购进一批某品牌的文化衫若干件，很快售完，该店又用 6300 元钱购进第二批这种文化衫，所进的件数比第一批多 40%，每件文化衫的进价比第一批每件文化衫的进价多 10 元，请解答下列问题：（1）求购进的第一批文化衫的件数；（2）为了取信于顾客，在这两批文化衫的销售中，售价保持了一致若售完这两批文化衫服装店的总利润不少于 4100 元钱，那么服装店销售该品牌文化衫每件的最低售价是多少元？【分析】 （1）设第一批购进文化衫 x 件，根据数量总价单价结合第二
30、批每件文化衫的进价比第一批每件文化衫的进价多 10 元，即可得出关于 x 的分式方程，解之经检验后即可得出结论；（2）根据第二批购进的件数比第一批多 40%，可求出第二批的进货数量，设该服装店销售该品牌文化衫每件的售价为 y 元，根据利润销售单价销售数量进货总价，即可得出关于 y 的一元一次不等式，解之取其内的最小值即可得出结论【解答】解：（1）设第一批购进文化衫 x 件，根据题意得： 10 ，4000+ = 6300(1+40%)解得：x50，经检验，x50 是原方程的解，且符合题意答：第一批购进文化衫 50 件（2）第二批购进文化衫（1+40%）5070（件） 设该服装店销售该品牌文化衫每
31、件的售价为 y 元，根据题意得：（50+70）y400063004100，解得：y120答：该服装店销售该品牌文化衫每件最低售价为 120 元22如图，在 RtABC 中，C90，AD 平分BAC 交 BC 于点 D，O 为 AB 上一点，经过点 A，D 的O 分别交 AB，AC 于点 E，F，连接 OF 交 AD 于点 G（1）求证：BC 是O 的切线；（2）设 ABx，AFy，试用含 x，y 的代数式表示线段 AD 的长；（3）若 BE8，sinB ，求 DG 的长，=513【分析】 （1）连接 OD，由 AD 为角平分线得到一对角相等，再由等边对等角得到一对角相等，等量代换得到内错角相等
32、，进而得到 OD 与 AC 平行，得到 OD 与 BC 垂直，即可得证；（2）连接 DF，由（1）得到 BC 为圆 O 的切线，由弦切角等于夹弧所对的圆周角，进而得到三角形 ABD 与三角形 ADF 相似，由相似得比例，即可表示出 AD；（3）连接 EF，设圆的半径为 r，由 sinB 的值，利用锐角三角函数定义求出 r 的值，由直径所对的圆周角为直角，得到 EF 与 BC 平行，得到 sinAEF sinB，进而求出 DG的长即可【解答】 （1）证明：如图，连接 OD，AD 为BAC 的角平分线，BADCAD，OAOD ，ODA OAD，ODA CAD ，ODAC，C90，ODC90，ODB
33、C，BC 为圆 O 的切线；（2）解：连接 DF，由（1）知 BC 为圆 O 的切线，FDCDAF，CDACFD，AFDADB，BADDAF，ABDADF， ，即 AD2ABAFxy，=则 AD ；= （3）解：连接 EF，在 RtBOD 中，sin B ，=513设圆的半径为 r，可得 ，+8=513解得：r5，AE10，AB18，AE 是直径，AFE C90，EFBC，AEF B，sinAEF ，=513AFAEsinAEF 10 ，513=5013AFOD， ，即 DG AD，=50135=1013 =1323AD ，= =185013=301313则 DG =1323301313=30
34、132323如图，已知抛物线的顶点为 A（1，4） ，抛物线与 y 轴交于点 B（0，3） ，与 x 轴交于C，D 两点点 P 是 x 轴上的一个动点（1）求此抛物线的解析式；（2）当 PA+PB 的值最小时，求点 P 的坐标；（3）抛物线上是否存在一点 Q（Q 与 B 不重合） ，使CDQ 的面积等于BCD 的面积？若存在，直接写出点 Q 的坐标；若不存在，请说明理由【分析】 （1）设抛物线顶点式解析式 ya（x1） 2+4，然后把点 B 的坐标代入求出 a的值，即可得解；（2）先求出点 B 关于 x 轴的对称点 B的坐标，连接 AB与 x 轴相交，根据轴对称确定最短路线问题，交点即为所求的
35、点 P，然后利用待定系数法求一次函数解析式求出直线 AB的解析式，再求出与 x 轴的交点即可（3）S CDQ S BCD 且 CD 是两三角形的公共底边知| yQ|y B3，据此得 yQ3 或yQ3，再分别求解可得【解答】解：（1）抛物线的顶点为 A（1，4） ，设抛物线的解析式 ya（x1） 2+4，把点 B（0，3）代入得，a+43，解得 a1，抛物线的解析式为 y（x1） 2+4；（2）点 B 关于 x 轴的对称点 B的坐标为（0，3） ，由轴对称确定最短路线问题，连接 AB与 x 轴的交点即为点 P，设直线 AB的解析式为 ykx+b（k0） ，则 ，k+b=4=3 解得 ，k=7=3直线 AB的解析式为 y7x 3，令 y0，则 7x30，解得 x ，=37所以，当 PA+PB 的值最小时的点 P 的坐标为（ ，0） 37（3）S CDQ S BCD ，且 CD 是两三角形的公共底边，|y Q|y B3，则 yQ3 或 yQ3，当 yQ3 时，（x1） 2+43，解得：x0 或 x2，则点 Q（2，3） ；当 yQ3 时，（x1） 2+43，解得：x1 或 x1 ，- 7 + 7则点 Q 坐标为（1 ， 3）或（1 ，3） ；- 7 + 7综上，点 Q 的坐标为（2，3 ）或（1 ，3）或（1 ，3） - 7 + 7
