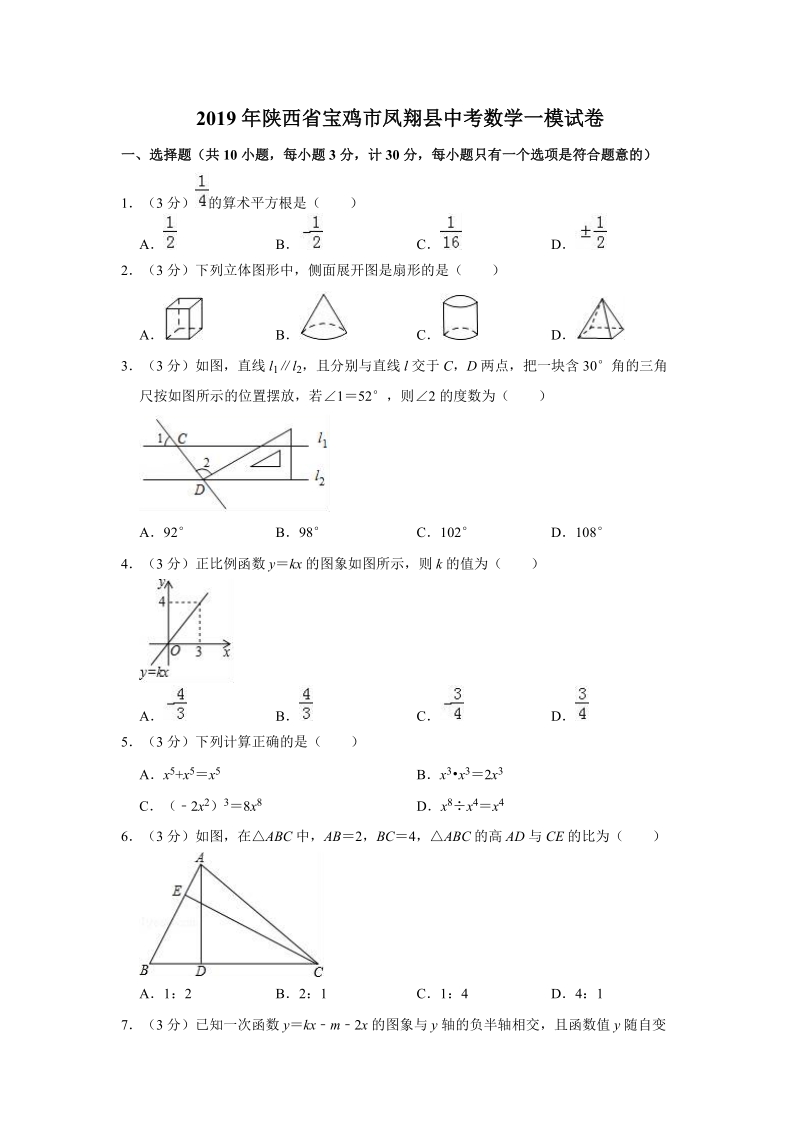
1、2019 年陕西省宝鸡市凤翔县中考数学一模试卷一、选择题（共 10 小题，每小题 3 分，计 30 分，每小题只有一个选项是符合题意的）1（3 分） 的算术平方根是（ ）A B C D2（3 分）下列立体图形中，侧面展开图是扇形的是（ ）A B C D3（3 分）如图，直线 l1l 2，且分别与直线 l 交于 C，D 两点，把一块含 30角的三角尺按如图所示的位置摆放，若152，则2 的度数为（ ）A92 B98 C102 D1084（3 分）正比例函数 ykx 的图象如图所示，则 k 的值为（ ）A B C D5（3 分）下列计算正确的是（ ）Ax 5+x5x 5 Bx 3x32x 3C（2
2、x 2） 38x 8 Dx 8x4x 46（3 分）如图，在ABC 中，AB2，BC 4，ABC 的高 AD 与 CE 的比为（ ）A1：2 B2：1 C1：4 D4：17（3 分）已知一次函数 ykxm2x 的图象与 y 轴的负半轴相交，且函数值 y 随自变量 x 的增大而减小，则下列结论正确的是（ ）Ak2，m 0 Bk2，m 0 Ck2，m0 Dk 0，m08（3 分）如图，ABCD 的对角线 AC 与 BD 相交于点 O，ABAC，若 AB4，BC，则 BD 的长是（ ）A8 B10 C9 D119（3 分）如图，O 是ABC 的外接圆，直径 AD4，ABCDAC，则 AC 的长为（
3、）A2 B2 C4 D210（3 分）若二次函数 y（k+1）x 22 x+k 的最高点在 x 轴上，则 k 的值为（ ）A1 B2 C1 D2二、填空题（共 4 小题，每小题 3 分，计 12 分）11（3 分）在实数 1， ，0， 中，最大的数 12（3 分）如图，若正五边形和正六边形有一边重合，则BAC 13（3 分）已知 A（x 1，y 1），B（x 2，y 2）都在反比例函数 y 的图象上若x1x24，则 y1y2 的值为 14（3 分）如图，四边形 ABCD，四边形 EBFG，四边形 HMPN 均是正方形，点E、F 、P、N 分别在边 AB、BC 、CD、AD 上，点 H、G、M
4、在 AC 上，阴影部分的面积依次记为 S1，S 2，则 S1：S 2 等于 三、解答题（共 11 小题，计 78 分解答应写出过程）15（5 分）计算： （ ）+|23 |16（5 分）解方程： 117（5 分）如图，已知ABC，利用尺规在 BC 上找一点 P，使得ABP 与ACP 均为直角三角形（不写作法，保留作图痕迹）18（5 分）如图，E、F 分别是矩形 ABCD 的对角线 AC 和 BD 上的点，且 AEDF 求证：BE CF19（7 分）中国飞人苏炳添以 6 秒 47 获得 2019 年国际田联伯明翰室内赛男子 60 米冠军，苏炳添夺冠掀起跑步热潮某校为了解该校八年级男生的短跑水平，
5、全校八年级男生中随机抽取了部分男生，对他们的短跑水平进行测试，并将测试成绩（满分 10 分）绘制成如下不完整的统计图表：组别 成绩/分 人数/人A 5 36B 6 32C 7 15D 8 8E 9 5F 10 m请你根据统计图表中的信息，解答下列问题：（1）填空：m ，n ；（2）所抽取的八年级男生短跑成绩的众数是 分，扇形统计图中 E 组的扇形圆心角的度数为 ；（3）求所抽取的八年级男生短跑的平均成绩20（7 分）汉江是长江最长的支流，在历史上占居重要地位，陕西省境内的汉江为汉江上游段李琳利用热气球探测器测量汉江某段河宽，如图，探测器在 A 处观测到正前方汉江两岸岸边的 B、C 两点，并测得
6、 B、C 两点的俯角分别为 45，30已知 A 处离地面的高度为 80m，河平面 BC 与地面在同一水平面上，请你求出汉江该段河宽BC（结果保留根号）21（7 分）快递公司为提高快递分拣的速度，决定购买机器人来代入工分拣两种型号的机器人的工作效率和价格如表：型号 甲 乙每台每小时分拣快递件数（件）1000 800每台价格（万元） 5 3该公司计划购买这两种型号的机器人共 10 台，并且使这 10 台机器人每小时分拣快递件数总和不少于 8500 件（1）设购买甲种型号的机器人 x 台，购买这 10 台机器人所花的费用为 y 万元，求 y 与x 之间的关系式；（2）购买几台甲种型号的机器人，能使购
7、买这 10 台机器人所花总费用最少？最少费用是多少？22（7 分）西安市历史文化底蕴深厚，旅游资源丰富，钟楼、大雁塔兵马俑三个景点是人们节假日游玩的热门景点（1）李辉从这三个景点中随机选取一个景点去游玩，求他去钟楼的概率；（2）张慧、王丽两名同学，各自从三个景点中随机选取一个作为周末游玩的景点，用树状图或列表法求他们同时选中大雁塔的概率23（8 分）如图，AB 是 O 的直径，点 C 在O 上，AD 和过 C 点的切线互相垂直，垂足为 D（1）求证：AC 平分DAB ；（2）若点 M 是 AB 的中点，CM 交 AB 于点 N，求证：BM 2MCMN24（10 分）如图，已知抛物线 C1：y
8、x 2+4，将抛物线 C1 沿 x 轴翻折，得到抛物线C2（1）求出抛物线 C2 的函数表达式；（2）现将抛物线 C1 向左平移 m 个单位长度，平移后得到的新抛物线的顶点为 M，与 x轴的交点从左到右依次为 A，B；将抛物线 C2 向右也平移 m 个单位长度，平移后得到的新抛物线的顶点为 N，与 x 轴交点从左到右依次为 D，E在平移过程中，是否存在以点 A，N，E，M 为顶点的四边形是矩形的情形？若存在，请求出此时 m 的值；若不存在，请说明理由25（12 分）（1）如图 1，A、B 是O 上的两个点，点 P 在O 上，且APB 是直角三角形，O 的半径为 1请在图 1 中画出点 P 的位
9、置；当 AB1 时，APB ；（2）如图 2，O 的半径为 5，A、B 为O 外固定两点（O、A、B 三点不在同一直线上），且 OA9，P 为O 上的一个动点（点 P 不在直线 AB 上），以 PA 和 AB 为作平行四边形 PABC，求 BC 的最小值并确定此时点 P 的位置；（3）如图 3，A、B 是O 上的两个点，过 A 点作射线 AMAB，AM 交 O 于点 C，若AB3，AC4 ，点 D 是平面内的一个动点，且 CD2，E 为 BD 的中点，在 D 的运动过程中，求线段 AE 长度的最大值与最小值2019 年陕西省宝鸡市凤翔县中考数学一模试卷参考答案与试题解析一、选择题（共 10 小
10、题，每小题 3 分，计 30 分，每小题只有一个选项是符合题意的）1（3 分） 的算术平方根是（ ）A B C D【分析】直接根据算术平方根的定义即可求出结果【解答】解：（ ） 2 故选：A【点评】此题主要考查了算术平方根的定义，解题的关键是算术平方根必须是正数，注意平方根和算术平方根的区别2（3 分）下列立体图形中，侧面展开图是扇形的是（ ）A B C D【分析】圆锥的侧面展开图是扇形【解答】解：根据圆锥的特征可知，侧面展开图是扇形的是圆锥故选：B【点评】解题时勿忘记圆锥的特征及圆锥展开图的情形3（3 分）如图，直线 l1l 2，且分别与直线 l 交于 C，D 两点，把一块含 30角的三角尺
11、按如图所示的位置摆放，若152，则2 的度数为（ ）A92 B98 C102 D108【分析】依据 l1l 2，即可得到1352，再根据 430，即可得出从21803498【解答】解：如图，l 1l 2，1352，又430，218034180523098，故选：B【点评】此题主要考查了平行线的性质，三角板的特征，角度的计算，解本题的关键是利用平行线的性质4（3 分）正比例函数 ykx 的图象如图所示，则 k 的值为（ ）A B C D【分析】由函数图象可知点（3，4）在函数上，因此将此点代入函数解析式即可求得 k值【解答】解：由图知，点（3，4）在函数 ykx 上，3k4，解得：k故选：B【点
12、评】本题考查用待定系数法求正比例函数解析式，为基础题关键在于通过读函数图象得到图象上点的坐标代入求解即可5（3 分）下列计算正确的是（ ）Ax 5+x5x 5 Bx 3x32x 3C（2x 2） 38x 8 Dx 8x4x 4【分析】分别根据合并同类项法则、同底数幂的乘法、积的乘方与幂的乘方和同底数幂的除法法则逐一计算可得【解答】解：Ax 5+x52x 5，此选项错误；Bx 3x3x 6，此选项错误；C（2x 2） 38x 6，此选项错误；Dx 8x4x 4，此选项正确；故选：D【点评】本题主要考查幂的乘方与积的乘方，解题的关键是掌握合并同类项法则、同底数幂的乘法、积的乘方与幂的乘方和同底数幂
13、的除法法则6（3 分）如图，在ABC 中，AB2，BC 4，ABC 的高 AD 与 CE 的比为（ ）A1：2 B2：1 C1：4 D4：1【分析】利用ABC 的面积公式列出方程求解即可【解答】解：S ABC ABCE BCAD，AB2，BC 4， 2CE 4AD， 故选：A【点评】本题考查了三角形的面积，利用同一个三角形的面积的两种表示列出方程是解题的关键7（3 分）已知一次函数 ykxm2x 的图象与 y 轴的负半轴相交，且函数值 y 随自变量 x 的增大而减小，则下列结论正确的是（ ）Ak2，m 0 Bk2，m 0 Ck2，m0 Dk 0，m0【分析】由一次函数 ykxm2x 的图象与
14、y 轴的负半轴相交且函数值 y 随自变量 x的增大而减小，可得出 k20、m 0，解之即可得出结论【解答】解：一次函数 ykxm2x 的图象与 y 轴的负半轴相交，且函数值 y 随自变量 x 的增大而减小，k20，m 0，k2，m0故选：A【点评】本题考查了一次函数的性质，根据一次函数的性质找出 k20、m0 是解题的关键8（3 分）如图，ABCD 的对角线 AC 与 BD 相交于点 O，ABAC，若 AB4，BC，则 BD 的长是（ ）A8 B10 C9 D11【分析】利用平行四边形的性质和勾股定理易求 AC 的长，得出 OA 的长，再由勾股定理求出 OB 的长，即可得出 BD 的长【解答】
15、解：ABCD 的对角线 AC 与 BD 相交于点 O，BODO ，AO CO，ABAC，AB4，BC ，AC 6，OA AC3，OB 5，BD2BO 10，故选：B【点评】本题考查了平行四边形的性质以及勾股定理的运用，熟练掌握平行四边形的性质，由勾股定理求出 OB 是解题关键9（3 分）如图，O 是ABC 的外接圆，直径 AD4，ABCDAC，则 AC 的长为（ ）A2 B2 C4 D2【分析】连接 CD，由圆周角定理得出ACD90，ADCABC，证出ADCDAC，得出 AC DC，ACD 是等腰直角三角形，得出 AD AC，即可的 AC 的长【解答】解：连接 CD，如图所示：AD 是 O 的
16、直径，ACD90，ADCABC，ABCDAC，ADCDAC，ACDC，ACD 是等腰直角三角形，AD AC，AC 2 ，故选：A【点评】本题考查了圆周角定理、等腰直角三角形的判定与性质、勾股定理；熟练掌握圆周角定理，证明ACD 是等腰直角三角形是解题关键10（3 分）若二次函数 y（k+1）x 22 x+k 的最高点在 x 轴上，则 k 的值为（ ）A1 B2 C1 D2【分析】直接利用二次函数的性质得出b 24ac0，进而得出答案【解答】解：二次函数 y（k+1）x 22 x+k 的最高点在 x 轴上，b 24ac0，即 84k（k +1）0，解得：k 11，k 22，当 k1 时，k+10
17、，此时图象有最低点，不合题意舍去，则 k 的值为：2故选：D【点评】此题主要考查了二次函数的最值，正确掌握二次函数的性质是解题关键二、填空题（共 4 小题，每小题 3 分，计 12 分）11（3 分）在实数 1， ，0， 中，最大的数 【分析】根据正实数都大于 0，负实数都小于 0，正实数大于一切负实数，两个负实数绝对值大的反而小可得答案【解答】解：在实数 1， ，0， 中， 10 ，最大的数是 故答案为： 【点评】此题主要考查了实数的大小比较，关键是掌握实数比较大小的法则12（3 分）如图，若正五边形和正六边形有一边重合，则BAC 132 【分析】根据正多边形的内角，角的和差，可得答案【解答
18、】解：正五边形的内角为 108，正六边形的内角为 120，BAC360108120132，故答案为：132【点评】本题考查了多边形的内角与外角，利用正多边形的内角是解题关键13（3 分）已知 A（x 1，y 1），B（x 2，y 2）都在反比例函数 y 的图象上若x1x24，则 y1y2 的值为 9 【分析】根据反比例函数图象上点的坐标特征得到 y1 ，y 2 ，再把它们相乘，然后把 x1x23 代入计算即可【解答】解：根据题意得 y1 ，y 2 ，所以 y1y2 ， 9故答案为9【点评】本题考查了反比例函数图象上点的坐标特征：反比例函数 y （k 为常数，k0）的图象是双曲线，图象上的点（x
19、，y ）的横纵坐标的积是定值 k，即 xyk14（3 分）如图，四边形 ABCD，四边形 EBFG，四边形 HMPN 均是正方形，点E、F 、P、N 分别在边 AB、BC 、CD、AD 上，点 H、G、M 在 AC 上，阴影部分的面积依次记为 S1，S 2，则 S1：S 2 等于 4：9 【分析】设 DPDNm，则PN m，PC 2m，AD CD3m，AC 3 m，CG AG m，求出两个阴影部分的面积即可解决问题【解答】解：设 DPDNm，则PN m，PC 2m，AD CD3m，AC 3 m，CG AG m，S 1 m2，S 2 CG2 m2， ，故答案为 4：9【点评】本题考查正方形的性质
20、，勾股定理等知识，解题的关键是学会利用参数解决问题，属于中考常考题型三、解答题（共 11 小题，计 78 分解答应写出过程）15（5 分）计算： （ ）+|23 |【分析】根据负指数幂的性质，绝对值的性质及算术平方根的定义求解即可【解答】解：原式6 +3 2（2）3 【点评】此题主要考查了实数的运算，正确化简各数是解题的关键16（5 分）解方程： 1【分析】先去分母，转化为一元一次方程，解一元一次方程，检验后即可得到答案【解答】解：方程两边同时乘以（x+2）（x2）得：x （ x2）1x 24，整理得：2x14，解得：x ，经检验：x 是方程的解，即原方程的解是：x 【点评】此题主要考查了解分
21、式方程，掌握解分式方程的步骤是解本题的关键，注意要检验17（5 分）如图，已知ABC，利用尺规在 BC 上找一点 P，使得ABP 与ACP 均为直角三角形（不写作法，保留作图痕迹）【分析】过 A 点作 BC 的垂线，垂足为 P，点 P 满足条件【解答】解：如图，点 P 为所作【点评】本题考查了作图复杂作图：复杂作图是在五种基本作图的基础上进行作图，一般是结合了几何图形的性质和基本作图方法解决此类题目的关键是熟悉基本几何图形的性质18（5 分）如图，E、F 分别是矩形 ABCD 的对角线 AC 和 BD 上的点，且 AEDF 求证：BE CF【分析】根据矩形对角线的性质，矩形对角线互相平分且相等
22、，可知EOFO，BO CO ，BOECOF，可知BOECOF，即可得出 BECF【解答】证明：矩形 ABCD 的对角线为 AC 和 BD，AOCOBODO，E、F 分别是矩形 ABCD 的对角线 AC 和 BD 上的点，AEDF ，EOFO ，在BOE 和COF 中，BOECOF（SAS ），BECF【点评】本题考查了矩形对角线互相平分且相等，全等三角形的判定方法以及全等三角形对应边相等的性质，难度适中19（7 分）中国飞人苏炳添以 6 秒 47 获得 2019 年国际田联伯明翰室内赛男子 60 米冠军，苏炳添夺冠掀起跑步热潮某校为了解该校八年级男生的短跑水平，全校八年级男生中随机抽取了部分男
23、生，对他们的短跑水平进行测试，并将测试成绩（满分 10 分）绘制成如下不完整的统计图表：组别 成绩/分 人数/人A 5 36B 6 32C 7 15D 8 8E 9 5F 10 m请你根据统计图表中的信息，解答下列问题：（1）填空：m 4 ，n 15 ；（2）所抽取的八年级男生短跑成绩的众数是 5 分，扇形统计图中 E 组的扇形圆心角的度数为 18 ；（3）求所抽取的八年级男生短跑的平均成绩【分析】（1）根据 B 组 32 人占总人数的 32%求得总人数即可求得 m，然后求得 C 组所占的百分比即可求得 n 的值；（2）利用众数的定义求得众数即可；求得 E 组所占的百分比即可求得所在扇形的圆心
24、角的度数；（3）利用平均数的定义直接计算即可【解答】解：（1）B 组的有 32 人，占 32%，被调查的人数为 3232% 100 人，m1003632158 54，1510015%，n15，故答案为：4，15；（2）成绩为 5 分的有 36 人，最多，所以众数为 5 分；510036018，扇形统计图中 E 组的扇形圆心角的度数为 18，故答案为：5，18；（3）所抽取的八年级男生短跑的平均成绩为：6.26（分）【点评】本题考查扇形统计图、统计表、用样本估计总体，解答本题的关键是明确题意，利用数形结合的思想解答，注意 n 和 n%的区别20（7 分）汉江是长江最长的支流，在历史上占居重要地位
25、，陕西省境内的汉江为汉江上游段李琳利用热气球探测器测量汉江某段河宽，如图，探测器在 A 处观测到正前方汉江两岸岸边的 B、C 两点，并测得 B、C 两点的俯角分别为 45，30已知 A 处离地面的高度为 80m，河平面 BC 与地面在同一水平面上，请你求出汉江该段河宽BC（结果保留根号）【分析】过 A 作 ADBD 于点 D，根据正切的概念解答即可【解答】解：过 A 作 ADBD 于点 D，在 Rt ADB 中，ABD45BDAD 8，在 Rt ACD 中， ACD30 tanACD ，CD 80 80 ，BCCDBD80 80该汉江段河宽 BC 为（80 80）米【点评】本题考查的是解直角三
26、角形的应用，理解仰角和俯角的概念、掌握锐角三角函数的概念是解题的关键，解答时，注意正确作出辅助线构造直角三角形21（7 分）快递公司为提高快递分拣的速度，决定购买机器人来代入工分拣两种型号的机器人的工作效率和价格如表：型号 甲 乙每台每小时分拣快递件数（件）1000 800每台价格（万元） 5 3该公司计划购买这两种型号的机器人共 10 台，并且使这 10 台机器人每小时分拣快递件数总和不少于 8500 件（1）设购买甲种型号的机器人 x 台，购买这 10 台机器人所花的费用为 y 万元，求 y 与x 之间的关系式；（2）购买几台甲种型号的机器人，能使购买这 10 台机器人所花总费用最少？最少
27、费用是多少？【分析】（1）根据总费用甲种型号机器人的费用+乙种机器人的费用，求出 y 与 x 的关系式即可；（2）根据这 10 台机器人每小时分拣快递件数总和不少于 8500 件，列出不等式，求得x 的取值范围，再利用（1）中函数，求出 y 的最小值即可【解答】解：（1）y 与 x 之间的函数关系式为：y5x+3（10 x）2x+30 ；（2）由题可得：1000x+800（10x）8500，解得 x ，20，y 随 x 的增大而增大，当 x3 时，y 取得最小值，y 最小 23+3036，购买 3 台甲种型号的机器人，能使购买这 10 台机器人所花总费用最少，最少费用为36 万元【点评】本题主
28、要考查函数的应用，解决此题的关键是熟练掌握函数的性质22（7 分）西安市历史文化底蕴深厚，旅游资源丰富，钟楼、大雁塔兵马俑三个景点是人们节假日游玩的热门景点（1）李辉从这三个景点中随机选取一个景点去游玩，求他去钟楼的概率；（2）张慧、王丽两名同学，各自从三个景点中随机选取一个作为周末游玩的景点，用树状图或列表法求他们同时选中大雁塔的概率【分析】（1）直接利用概率公式计算可得；（2）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与他们同时选中大雁塔的情况，再利用概率公式求解即可求得答案【解答】解：（1）他去钟楼的概率为 （2）分别用 1，2，3 表示钟楼、大雁塔、兵马俑，画树状图得：共
29、有 9 种等可能的结果，他们同时选中大雁塔的只有 1 种情况，P（他们同时选中大雁塔） 【点评】此题考查了列表法或树状图法求概率以及扇形与条形统计图的知识注意掌握扇形统计图与条形统计图的对应关系用到的知识点为：概率所求情况数与总情况数之比23（8 分）如图，AB 是 O 的直径，点 C 在O 上，AD 和过 C 点的切线互相垂直，垂足为 D（1）求证：AC 平分DAB ；（2）若点 M 是 AB 的中点，CM 交 AB 于点 N，求证：BM 2MCMN【分析】（1）根据切线的性质，只需求证 ADOC，即可求证（2）证明MBN MCB 即可求解【解答】解：（1）证明：如图，连接 OC，ACCD
30、为O 的切线，OCCD又ADCD，ADOCDACACO又OAOC，CAOACODACCAOAC 平分DAB ；（2）连接 MA点 M 是弧 AB 的中点，弧 AM弧 BMBCMABMBMCBMNMBNMCB BM 2MCMN【点评】此题主要考查圆切线的性质，角平分线，平行线的性质，相似三角形的性质熟记并灵活运用切线的性质：（1）经过切点垂直于切线的线段必是此圆的直径或半径（2）圆的切线垂直于经过切点的半径，这是解题的关键24（10 分）如图，已知抛物线 C1：y x 2+4，将抛物线 C1 沿 x 轴翻折，得到抛物线C2（1）求出抛物线 C2 的函数表达式；（2）现将抛物线 C1 向左平移 m
31、 个单位长度，平移后得到的新抛物线的顶点为 M，与 x轴的交点从左到右依次为 A，B；将抛物线 C2 向右也平移 m 个单位长度，平移后得到的新抛物线的顶点为 N，与 x 轴交点从左到右依次为 D，E在平移过程中，是否存在以点 A，N，E，M 为顶点的四边形是矩形的情形？若存在，请求出此时 m 的值；若不存在，请说明理由【分析】（1）抛物线翻折前后顶点关于 x 轴对称，a 互为相反数；（2）连接 AN，NE，EM，MA，M，N 关于原点 O 对称 OMON，A，E 关于原点 O 对称 OAOE ，判断四边形 ANEM 为平行四边形；若 AM2+ME2AE 2，解得 m3，即可求解；【解答】解：
32、（1）抛物线 C1 的顶点为（0，4），沿 x 轴翻折后顶点的坐标为（04），抛物线 C2 的函数表达式为 yx 24；（2）存在连接 AN，NE，EM，MA ，依题意可得：M（m，4），N （m ，4），M，N 关于原点 O 对称 OMON，原 C1、C 2 抛物线与 x 轴的两个交点分别（2，0），（ 2，0），A（2m，0），E（2+m，0），A，E 关于原点 O 对称，OAOE四边形 ANEM 为平行四边形，AM 22 2+4220，ME2（2+m+m） 2+424m 2+8m+20，AE2（2+m+2+m） 24m 2+16m+16，若 AM2+ME2 AE2，20+4m 2+8m+
33、204m 2+16m+16，解得 m3，此时AME 是直角三角形，且AME 90，当 m3 时，以点 A，N，E，M 为顶点的四边形是矩形【点评】本题考查二次函数关于 x 轴对称，平行四边形的判定，矩形的性质找准二次函数图象变化后对应的点是解决翻折后函数图象的关键；能够在平面直角坐标系中，通过坐标点的特点判定平行四边形，利用勾股定理判定矩形是解决本题的关键25（12 分）（1）如图 1，A、B 是O 上的两个点，点 P 在O 上，且APB 是直角三角形，O 的半径为 1请在图 1 中画出点 P 的位置；当 AB1 时，APB 30 ；（2）如图 2，O 的半径为 5，A、B 为O 外固定两点（
34、O、A、B 三点不在同一直线上），且 OA9，P 为O 上的一个动点（点 P 不在直线 AB 上），以 PA 和 AB 为作平行四边形 PABC，求 BC 的最小值并确定此时点 P 的位置；（3）如图 3，A、B 是O 上的两个点，过 A 点作射线 AMAB，AM 交 O 于点 C，若AB3，AC4 ，点 D 是平面内的一个动点，且 CD2，E 为 BD 的中点，在 D 的运动过程中，求线段 AE 长度的最大值与最小值【分析】（1）根据圆周角定理作图；根据直角三角形的性质解答；（2）根据平行四边形的性质得到 BCAP ，根据线段的性质计算；（3）连接 BC，根据勾股定理求出 BC，根据直角三角
35、形的性质求出 OA，根据三角形中位线定理求出 OE，根据三角形的三边关系解答即可【解答】解：（1）如图 1，APB 、AP B 是直角三角形；在 RtAPB 中，AB AP，APB 30，故答案为：30；（2）四边形 PABC 是平行四边形，BCAP，BC 的最小值即 AP 的最小值，当 P 为 OA 与 O 的交点时，AP 最小，AP 的最小值为 954，即 BC 的最小值为 4；（3）连接 BC，AMAB，CAB90，BC 是O 的直径，点 D 是平面内的一个动点，且 CD2，点 D 的运动路径为以 C 为圆心，以 2 为半径的圆，BC 是O 的直径，O 是 BC 的中点，在直角ABC 中，BC 5，O 是直角ABC 斜边 BC 上的中点，AO BC ，E 是 BD 的中点， O 是 BC 的中点OE CD 1，AE 的最小值是 AOOE ，最大值是 AO+OE 【点评】本题考查的是圆的知识，掌握平行四边形的性质、圆周角定理、三角形的三边关系是解题的关键
