1、2019 年浙江省宁波市宁海县前横初中中考数学模拟试卷一选择题（每小题 3 分，共 36 分，在每小题给出的四个选项中，只有一项符合题目要求）1 值等于（ ）A4 B4 C2 D22据媒体报道，我国因环境污染造成的巨大经济损失，每年高达 680 000 000 元，这个数用科学记数法表示正确的是（ ）A6.810 9 元 B6.810 8 元 C6.810 7 元 D6.810 6 元3计算 2a2a3 的结果是（ ）A2a 5 B2a 6 C4a 5 D4a 64在 RtABC 中，C90，AC3，BC 4，那么 cosB 的值是（ ）A B C D5如图，身高为 1.5 米的某学生想测量一
2、棵大树的高度，她沿着树影 BA 由 B 向 A 走去当走到 C 点时，她的影子顶端正好与树的影子顶端重合，测得 BC3 米，CA1 米，则树的高度为（ ）A4.5 米 B6 米 C3 米 D4 米6如图，在纸上剪下一个圆形和一个扇形的纸片，使之恰好能围成一个圆锥模型，若圆的半径为 r，扇形的圆心角等于 120，则围成的圆锥模型的高为（ ）Ar B2 r C r D3r7小兰画了一个函数 y 的图象如图，那么关于 x 的分式方程 2 的解是（ ）Ax1 Bx2 Cx3 Dx 48 从长度分别为 3、5、7、9 的 4 条线段中任取 3 条作边，能组成三角形的概率为（ ）A B C D9如图，直线
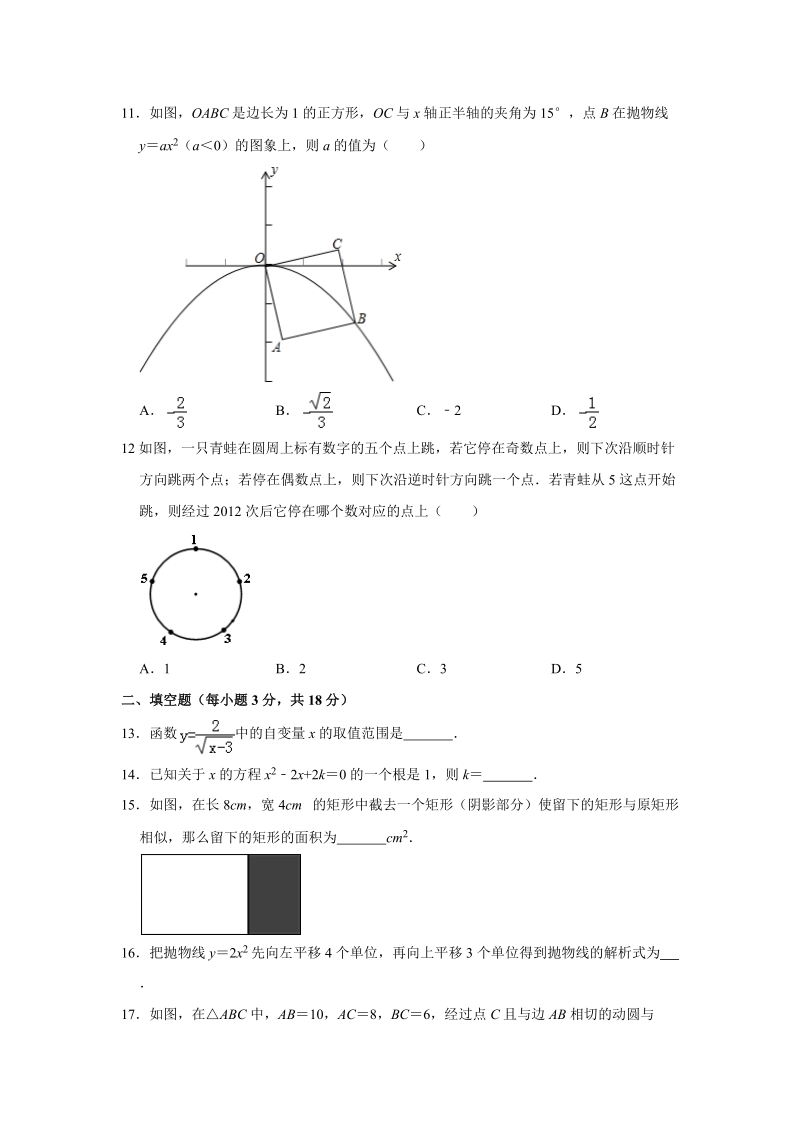
3、 l1l 2，O 与 l1 和 l2 分别相切于点 A 和点 B点 M 和点 N 分别是 l1 和 l2上的动点，MN 沿 l1 和 l2 平移O 的半径为 1，160下列结论错误的是（ ）AB若 MN 与 O 相切，则C若MON90，则 MN 与O 相切Dl 1 和 l2 的距离为 210如图，已知 A 点坐标为（5，0） ，直线 yx +b（b0）与 y 轴交于点 B，连接AB， 75 ，则 b 的值为（ ）A3 B C4 D11如图，OABC 是边长为 1 的正方形，OC 与 x 轴正半轴的夹角为 15，点 B 在抛物线yax 2（a0）的图象上，则 a 的值为（ ）A B C2 D12
4、 如图，一只青蛙在圆周上标有数字的五个点上跳，若它停在奇数点上，则下次沿顺时针方向跳两个点；若停在偶数点上，则下次沿逆时针方向跳一个点若青蛙从 5 这点开始跳，则经过 2012 次后它停在哪个数对应的点上（ ）A1 B2 C3 D5二、填空题（每小题 3 分，共 18 分）13函数 中的自变量 x 的取值范围是 14已知关于 x 的方程 x22x +2k0 的一个根是 1，则 k 15如图，在长 8cm，宽 4cm 的矩形中截去一个矩形（阴影部分）使留下的矩形与原矩形相似，那么留下的矩形的面积为 cm 216把抛物线 y2x 2 先向左平移 4 个单位，再向上平移 3 个单位得到抛物线的解析式
5、为 17如图，在ABC 中，AB10，AC 8，BC 6，经过点 C 且与边 AB 相切的动圆与CA，CB 分别相交于点 P，Q，则线段 PQ 长度的最小值是 18如图，已知点 A（0，2） 、B（ ，2） 、C （0，4） ，过点 C 向右作平行于 x 轴的射线，点 P 是射线上的动点，连接 AP，以 AP 为边在其左侧作等边APQ，连接 PB、BA 若四边形 ABPQ 为梯形，则：（1）当 AB 为梯形的底时，点 P 的横坐标是 ；（2）当 AB 为梯形的腰时，点 P 的横坐标是 三、解答题（第 19 题 6 分，第 20-22 题各 8 分，第 23-24 题 10 分，第 25 题 1
6、2 分，第 26题 14 分，共 76 分）19计算： 20求代数式的值： ，其中 21今年起，兰州市将体育考试正式纳入中考考查科目之一，其等级作为考生录取的重要依据之一某中学为了了解学生体育活动情况，随即调查了 720 名初二学生，调查内容是：“每天锻炼是否超过 1 小时及未超过 1 小时的原因” ，利用所得的数据制成了扇形统计图和频数分布直方图根据图示，解答下列问题：（1）若在被调查的学生中随机选出一名学生测试其体育成绩，选出的是“每天锻炼超过 1 小时”的学生的概率是多少？（2） “没时间”锻炼的人数是多少？并补全频数分布直方图；（3）兰州市区初二学生约为 2.4 万人，按此调查，可以估
7、计 2011 年兰州市区初二学生中每天锻炼未超过 1 小时的学生约有多少万人？（4）请根据以上结论谈谈你的看法22如图，AB 为量角器（半圆 O）的直径，等腰直角BCD 的斜边 BD 交量角器边缘于点G，直角边 CD 切量角器于读数为 60的点 E 处（即弧 AE 的度数为 60） ，第三边交量角器边缘于点 F 处（1）求量角器在点 G 处的读数 （90180） ；（2）若 AB12cm，求阴影部分面积23我市水产养殖专业户王大爷承包了 30 亩水塘，分别养殖甲鱼和桂鱼，有关成本、销售情况如下表：养殖种类 成本（万元/亩） 销售额（万元/亩）甲鱼 2.4 3桂鱼 2 2.5（1）2018 年，
8、王大爷养殖甲鱼 20 亩，桂鱼 10 亩，求王大爷这一年共收益多少万元？（收益销售额成本）（2）2019 年，王大爷继续用这 30 亩水塘全部养殖甲鱼和桂鱼，计划投入成本不超过70 万元若每亩养殖的成本、销售额与 2010 年相同，要获得最大收益，他应养殖甲鱼和桂鱼各多少亩？（3）已知甲鱼每亩需要饲料 500kg，桂鱼每亩需要饲料 700kg，根据（2）中的养殖亩数，为了节约运输成本，实际使用的运输车辆每次装载饲料的总量是原计划每次装载总量的 2 倍，结果运输养殖所需要全部饲料比原计划减少了 2 次，求王大爷原定的运输车辆每次可装载饲料多少千克？24 （1）动手操作：如图 ，将矩形纸片 ABC
9、D 折叠，使点 D 与点 B 重合，点 C 落在点 c处，折痕为 EF，若ABE 20，那么EFC 的度数为 （2）观察发现：小明将三角形纸片 ABC（ABAC ）沿过点 A 的直线折叠，使得 AC 落在 AB 边上，折痕为 AD，展开纸片（如图 ） ；再次折叠该三角形纸片，使点 A 和点 D 重合，折痕为EF，展平纸片后得到AEF（如图） 小明认为AEF 是等腰三角形，你同意吗？请说明理由（3）实践与运用：将矩形纸片 ABCD 按如下步骤操作：将纸片对折得折痕 EF，折痕与 AD 边交于点 E，与 BC 边交于点 F；将矩形 ABFE 与矩形 EFCD 分别沿折痕 MN 和 PQ 折叠，使点
10、 A、点 D 都与点 F 重合，展开纸片，此时恰好有 MPMN PQ（如图） ，求MNF 的大小25如图，在平面直角坐标系中，二次函数 yax 2+6x+c 的图象经过点 A（4，0） 、B（1 ，0） ，与 y 轴交于点 C，点 D 在线段 OC 上，OD t ，点 E 在第二象限，ADE90， tanDAE ，EFOD，垂足为 F（1）求这个二次函数的解析式；（2）求线段 EF、OF 的长（用含 t 的代数式表示） ；（3）当ECAOAC 时，求 t 的值26在半径为 4 的O 中，点 C 是以 AB 为直径的半圆的中点，ODAC ，垂足为 D，点E 是射线 AB 上的任意一点，DFAB，
11、DF 与 CE 相交于点 F，设 EFx，DFy（1）如图 1，当点 E 在射线 OB 上时，求 y 关于 x 的函数解析式，并写出函数定义域；（2）如图 2，当点 F 在O 上时，求线段 DF 的长；（3）如果以点 E 为圆心、EB 为半径的圆与 O 相切，求线段 DF 的长参考答案一选择题（每小题 3 分，共 36 分，在每小题给出的四个选项中，只有一项符合题目要求）1 【解答】解： 表示 16 的算术平方根， 的值等于 4故选：B2 【解答】解：680 000 0006.810 8 元故选：B3 【解答】解：2a 2a32a 5故选：A4 【解答】解：RtABC 中，C90，AC3，BC
12、4，根据勾股定理 AB5cosB 故选：A5 【解答】解：如图：CDBE ，ACDABE，AC：ABCD：BE ，1：41.5：BE，BE6m故选：B6 【解答】解：圆的半径为 r，扇形的弧长等于底面圆的周长得出 2r设圆锥的母线长为 R，则 2 r，解得：R3r根据勾股定理得圆锥的高为 2 r，故选：B7 【解答】解：由图可知当 x3 时，y0，即 0，解得 a3，当 2 时，解得 x1故选：A8 【解答】解：根据三角形三边关系定理：三角形两边之和大于第三边，从长度分别为 3、5、7、9 的 4 条线段中任取 3 条作边，能组成三角形的是：3，5，7；5，7，9；3，7，9；共三组，能组成三
13、角形的概率为 34 ，故选：A9 【解答】解：A、平移 MN 使点 B 与 N 重合，160，AB2，解直角三角形得，正确；B、当 MN 与圆相切时，M， N 在 AB 左侧以及 M，N 在 A，B 右侧时，AM 或 ，错误；C、若MON90，连接 NO 并延长交 MA 于点 C，则 AOCBON，故 CONO ，MONMOC，故 MN 上的高为 1，即 O 到 MN 的距离等于半径正确；D、l 1l 2，两平行线之间的距离为线段 AB 的长，即直径 AB2，正确故选：B10 【解答】解：由直线 yx+b（b0） ，可知145，75，ABO180457560，OBOA tanABO 点 B 的
14、坐标为（0， ） ，b 故选：B11 【解答】解：如图，连接 OB，过 B 作 BDx 轴于 D；则BOC45，BOD30 ；已知正方形的边长为 1，则 OB ；RtOBD 中，OB ，BOD30，则：BD OB ，OD OB ；故 B（ ， ） ，代入抛物线的解析式中，得：（ ） 2a ，解得 a ；故选：B12 【解答】解：第 1 次跳后落在 2 上；第 2 次跳后落在 1 上；第 3 次跳后落在 3 上；第 4 次跳后落在 5 上；4 次跳后一个循环，依次在 2，1，3，5 这 4 个数上循环，20124503，应落在 5 上，故选：D二、填空题（每小题 3 分，共 18 分）13 【解
15、答】解：根据题意得：x30，解得：x3；故答案为 x314 【解答】解：根据题意，得x1 满足关于 x 的方程 x2 2x+2k0，则12+2k0，解得，k ；故答案是： 15 【解答】解：设留下的矩形的宽为 x，留下的矩形与原矩形相似， ，x2，留下的矩形的面积为：248（cm 2）故答案为：816 【解答】解：抛物线 y2x 2 先向左平移 4 个单位得到解析式：y2（x+4） 2，再向上平移 3 个单位得到抛物线的解析式为：y2（x+4） 2+3故答案为：y2（x +4） 2+317 【解答】解：如图，AB10，AC8，BC 6，AB 2AC 2+BC2，ACB90，PQ 是 F 的直径
16、，设 QP 的中点为 F，圆 F 与 AB 的切点为 D，连接 FD，连接 CF，CD，则 FDABFC+FDPQ，CF+FDCD，当点 F 在直角三角形 ABC 的斜边 AB 的高上 CD 时，PQCD 有最小值CDBCACAB4.8故答案为 4.818 【解答】解：（1）如图 1：当 AB 为梯形的底时，PQAB，Q 在 CP 上，APQ 是等边三角形，CPx 轴，AC 垂直平分 PQ，A（0，2） ，C（0，4） ，AC2，PCACtan302 ，当 AB 为梯形的底时，点 P 的横坐标是： ；（2）如图 2，当 AB 为梯形的腰时，AQBP，Q 在 y 轴上，BPy 轴，CPx 轴，四
17、边形 ABPC 是平行四边形，CPAB2 ，如图 3，当 C 与 P 重合时，A（0，2） 、B（ ，2） ，tanAPB ，APB 60，APQ 是等边三角形，PAQ60，ACBPAQ，AQBP，当 C 与 P 重合时，四边形 ABPQ 以 AB 为腰的梯形，此时点 P 的横坐标为 0；当 AB 为梯形的腰时，点 P 的横坐标是：0 或 2 故答案为：（1） ， （2）0 或 2 三、解答题（第 19 题 6 分，第 20-22 题各 8 分，第 23-24 题 10 分，第 25 题 12 分，第 26题 14 分，共 76 分）19 【解答】解：原式1+2 13 20 【解答】解： +（
18、x+2） +x+2 +x+2x+ ，当 x 时，原式 + 321 【解答】解：（1）利用超过 1 小时的占 90，得出 ，选出的恰好是“每天锻炼超过 1 小时”的学生的概率是 ；（2）720 540（人） ，54012020400 人，“没时间”锻炼的人数是 400；（3）2.4（1 ）1.8（万人） ，2011 年兰州市初二学生每天锻炼未超过 1 小时约有 1.8 万人（4）根据同学们的锻炼身体时间情况可以发现，同学们需要加强锻炼说明：内容健康，能符合题意即可22 【解答】解：连接 OE，OF，（1）CD 切半圆 O 于点 EOE CD，BD 为等腰直角BCD 的斜边， BCCD，D CBD
19、45，OEBCABCAOE60，ABGABCCBD604515弧 AG 的度数2ABG30，量角器在点 G 处的读数 弧 AG 的度数30 （4 分）（2）OFOB AB6cm，ABC60，OBF 为正三角形，BOF60，S 扇形 6（cm 2） ，S OBF 629 （cm 2） ，S 阴影 S 扇形 S OBF （69 ）cm 2阴影部分的面积为（69 ）cm 2 （4 分）23 【解答】解：（1）2010 年王大爷的收益为：20（32.4）+10（2.52）17（万元） ，答：王大爷这一年共收益 17 万元（2）设养殖甲鱼 x 亩，则养殖桂鱼（30x）亩，由题意得 2.4x+2（30x
20、）70解得 x25，又设王大爷可获得收益为 y 万元，则 y0.6x+0.5 （30x ） ，即 y x+15函数值 y 随 x 的增大而增大，当 x25 时，可获得最大收益答：要获得最大收益，应养殖甲鱼 25 亩，桂鱼 5 亩（3）设大爷原定的运输车辆每次可装载饲料 a（kg） ，由（2）得，共需要饲料为 50025+700516000（kg） ，根据题意得 2，解得 a4000，把 a4000 代入原方程公分母得，2a2400080000，故 a4000 是原方程的解答：王大爷原定的运输车辆每次可装载饲料 4000kg24 【解答】解：（1）在直角三角形 ABE 中，ABE20，AEB 7
21、0，BED110，根据折叠重合的角相等，得BEFDEF55ADBC，EFC125，再根据折叠的性质得到EFCEFC 125故答案为 125；（2）同意如图，设 AD 与 EF 交于点 G由折叠知，AD 平分BAC，所以BADCAD由折叠知，AGEDGE 90，所以AGEAGF 90，所以AEF AFE 所以 AEAF，即AEF 为等腰三角形（3）由题意得出：NMFAMNMNF ，MFNF，由对称性可知，MFPF，NFPF，而由题意得出：MPMN，MFMF ，在MNF 和MPF 中， ，MNFMPF（SSS） ，PMF NMF，而PMF+NMF+ MNF 180，即 3MNF180，MNF60，
22、25 【解答】解：（1）二次函数 yax 2+6x+c 的图象经过点 A（4，0） 、B（1，0） ， ，解得 ，这个二次函数的解析式为：y2x 2+6x+8；（2）EFDEDA 90DEF+EDF 90，EDF +ODA90，DEFODAEDFDAO ， ， ，EF t同理 ，DF2，OFt2（3）抛物线的解析式为：y2x 2+6x+8，C（0，8） ，OC8如图，连接 EC、AC，过 A 作 EC 的垂线交 CE 于 G 点ECAOAC，在GCA 与OAC 中，GCAOAC，CG4，AGOC8如图，过 E 点作 EMx 轴于点 M，则在 RtAEM 中，EMOF t 2，AM OA+OMO
23、A +EF4+ t，由勾股定理得：AE 2AM 2+EM2 ；在 Rt AEG 中，由勾股定理得：EG 在 RtECF 中，EF t， CFOCOFOCEM 8（t2）10t，CECG+ EG +4由勾股定理得：EF 2+CF2CE 2，即 ，解得 t110，t 26，当 t10 时，CF10100，不合题意舍去，t6另解：延长 CE 至 x 轴交于点 KECAOAC（已知）AKCK（等角对等边）设 OKx，则 AK4+x 在 Rt COK 中，CO8，OKx根据勾股定理得，CK ，根号 64+x24+x，解得 x6，CEFCKO （两角对应相等）EF：KOCF：CO，即 0.5t：610t：
24、8，解得 t626 【解答】解：（1）连接 OC在 O 中，AC 是 O 的弦，ODAC，CDADDFAB，CFEFDF AE （AO+ OE） 点 C 是以 AB 为直径的半圆的中点，COAB EFx，AOCO4，CE2x ，OE 2 y （4+2 ）2+ 定义域为 x2；（2）当点 F 在O 上时，连接 OC、OF EF CEOF4，OCOB AB4DF2+ 2+2 （3）当E 与O 外切于点 B 时，BE FECE 2OE 2CO 2，（2x） 2（x +4） 24 2，3x 28x320，x 1 ，x 2 （舍去） DF （AB +BE） （8+ ） 当 E 与O 内切于点 B 时， BEFECE 2OE 2CO 2，（2x） 2（4x ） 24 2，3x 2+8x320x 1 ，x 2 （舍去） DF （AB BE） （8 ） 当 E 与O 内切于点 A 时， AEFECE 2OE 2CO 2，（2x） 2（4x ） 24 2，3x 2+8x320x 1 ，x 2 （舍去） DF
