1、2019 年贵州省毕节市中考数学模拟试卷（二）一、选择题（本大题共 15 小题，满分 45 分，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得 3 分，选错、不选或选出的答案超过一个，均记零分）1（3 分）四个实数 0、 、3.14、2 中，最小的数是（ ）A0 B C3.14 D22（3 分）一年之中地球与太阳之间的距离随时间而变化，1 个天文单位是地球与太阳之间的平均距离，即 1.496 亿 km，用科学记数法表示 1.496 亿是（ ）A1.49610 7 B14.9610 8 C0.149610 8 D1.49610 83（3 分）下列计算正确的是（ ）
2、Aa 4ba2ba 2b B（ab） 2a 2b 2Ca 2a3a 6 D3a 2+2a2a 24（3 分）如图，ABEF ，CDEF，BAC50，则ACD（ ）A120 B130 C140 D1505（3 分）下列图形是中心对称图形的是（ ）A BC D6（3 分）下列几何体中，同一个几何体的主视图与俯视图不同的是（ ）A B C D7（3 分）不等式组 的解集在数轴上表示正确的是（ ）ABCD8（3 分）点 P（1，2）关于 y 轴对称的点的坐标是（ ）A（1，2） B（1，2） C（1，2） D（2，1）9（3 分）在 2016 年龙岩市初中体育中考中，随意抽取某校 5 位同学一分钟跳绳
3、的次数分别为：158，160，154，158，170，则由这组数据得到的结论错误的是（ ）A平均数为 160 B中位数为 158C众数为 158 D方差为 20.310（3 分）若 x2 是关于 x 的一元二次方程 x2+ axa 20 的一个根，则 a 的值为（ ）A1 或 4 B1 或4 C1 或4 D1 或 411（3 分）甲、乙两人用如图所示的两个转盘（每个转盘被分成面积相等的 3 个扇形）做游戏游戏规则：转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数时甲获胜；数字之和为奇数时乙获胜若指针落在分界线上，则需要重新转动转盘甲获胜的概率是（ ）A B C D12（3 分）如
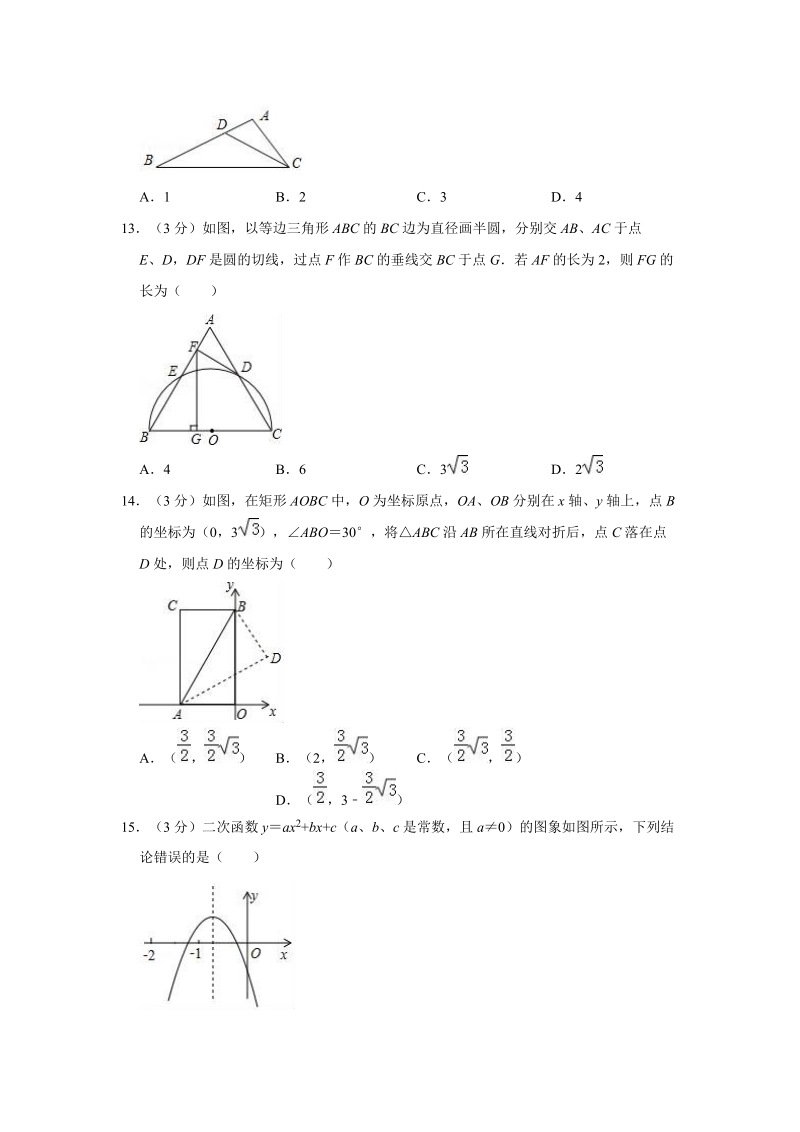
4、图，在ABC 中，点 D 是 AB 边上的一点，若ACDB，AD1，AC2，ADC 的面积为 1，则BCD 的面积为（ ）A1 B2 C3 D413（3 分）如图，以等边三角形 ABC 的 BC 边为直径画半圆，分别交 AB、AC 于点E、D， DF 是圆的切线，过点 F 作 BC 的垂线交 BC 于点 G若 AF 的长为 2，则 FG 的长为（ ）A4 B6 C3 D214（3 分）如图，在矩形 AOBC 中，O 为坐标原点，OA、OB 分别在 x 轴、y 轴上，点 B的坐标为（0，3 ）， ABO30，将ABC 沿 AB 所在直线对折后，点 C 落在点D 处，则点 D 的坐标为（ ）A（
5、， ） B（2， ） C（ ， ）D（ ，3 ）15（3 分）二次函数 yax 2+bx+c（a、b、c 是常数，且 a0）的图象如图所示，下列结论错误的是（ ）A4acb 2 Babc0 Cb+c3a Dab二、填空题（本大题共 5 小题，满分 25 分，只要求填写最后结果，每小题填对得 5 分）16（5 分）将 m3（x2）+m （2x）分解因式的结果是 17（5 分）我国明代数学读本算法统宗一书中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托如果 1 托为 5 尺，那么索长为 尺，竿子长为 尺18（5 分）如图，D 是等边 ABC 边 AB 上的点，AD2，
6、DB 4现将ABC 折叠，使得点 C 与点 D 重合，折痕为 EF，且点 E、F 分别在边 AC 和 BC 上，则 19（5 分）如图，RtABC 中，C90，BC15，tanA ，则 AB 20（5 分）如图，过原点 O 的直线与反比例函数 y1，y 2 的图象在第一象限内分别交于点A，B ，且 A 为 OB 的中点，若函数 y1 ，则 y2 与 x 的函数表达式是 三、解答题（本大题共 7 小题，满分 80 分.解答应写出必要的文字说明、证明过程或推演步骤）21（8 分）计算：（2） 3+ 2sin30+（2016） 022（8 分）先化简 （ x+1），然后从 x 的范围内选取一个合适的
7、整数作为 x 的值代入求值23（10 分）五月初，我市多地遭遇了持续强降雨的恶劣天气，造成部分地区出现严重洪涝灾害，某爱心组织紧急筹集了部分资金，计划购买甲、乙两种救灾物品共 2000 件送往灾区，已知每件甲种物品的价格比每件乙种物品的价格贵 10 元，用 350 元购买甲种物品的件数恰好与用 300 元购买乙种物品的件数相同（1）求甲、乙两种救灾物品每件的价格各是多少元？（2）经调查，灾区对乙种物品件数的需求量是甲种物品件数的 3 倍，若该爱心组织按照此需求的比例购买这 2000 件物品，需筹集资金多少元？24（12 分）某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计
8、图：频数 频率体育 40 0.4科技 25 a艺术 b 0.15其它 20 0.2请根据上图完成下面题目：（1）总人数为 人，a ，b （2）请你补全条形统计图（3）若全校有 600 人，请你估算一下全校喜欢艺术类学生的人数有多少？25（12 分）已知正方形 ABCD，P 为射线 AB 上的一点，以 BP 为边作正方形 BPEF，使点 F 在线段 CB 的延长线上，连接 EA、EC （1）如图 1，若点 P 在线段 AB 的延长线上，求证：EAEC；（2）若点 P 在线段 AB 上如图 2，连接 AC，当 P 为 AB 的中点时，判断ACE 的形状，并说明理由；如图 3，设 ABa，BPb，当
9、 EP 平分AEC 时，求 a：b 及AEC 的度数26（14 分）如图，在ABC 中，C90，BAC 的平分线交 BC 于点 D，点 O 在AB 上，以点 O 为圆心，OA 为半径的圆恰好经过点 D，分别交 AC，AB 于点 E，F（1）试判断直线 BC 与O 的位置关系，并说明理由；（2）若 BD2 ，BF2，求阴影部分的面积（结果保留 ）27（16 分）如图，对称轴为直线 x2 的抛物线 yx 2+bx+c 与 x 轴交于点 A 和点 B，与y 轴交于点 C，且点 A 的坐标为（ 1，0）（1）求抛物线的解析式；（2）直接写出 B、C 两点的坐标；（3）求过 O，B，C 三点的圆的面积（
10、结果用含 的代数式表示）注：二次函数 yax 2+bx+c（ a0）的顶点坐标为（ ， ）2019 年贵州省毕节市中考数学模拟试卷（二）参考答案与试题解析一、选择题（本大题共 15 小题，满分 45 分，在每小题给出的四个选项中，只有一个是正确的，请把正确的选项选出来，每小题选对得 3 分，选错、不选或选出的答案超过一个，均记零分）1（3 分）四个实数 0、 、3.14、2 中，最小的数是（ ）A0 B C3.14 D2【分析】正实数都大于 0，负实数都小于 0，正实数大于一切负实数，两个负实数绝对值大的反而小，据此判断即可【解答】解：根据实数比较大小的方法，可得3.140 2，所以最小的数是
11、3.14故选：C【点评】此题主要考查了实数大小比较的方法，要熟练掌握，解答此题的关键是要明确：正实数0负实数，两个负实数绝对值大的反而小2（3 分）一年之中地球与太阳之间的距离随时间而变化，1 个天文单位是地球与太阳之间的平均距离，即 1.496 亿 km，用科学记数法表示 1.496 亿是（ ）A1.49610 7 B14.9610 8 C0.149610 8 D1.49610 8【分析】科学记数法的表示形式为 a10n 的形式，其中 1|a| 10，n 为整数确定 n的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值1 时，n 是正数；当原数
12、的绝对值1 时，n 是负数【解答】解：数据 1.496 亿用科学记数法表示为 1.496108，故选：D【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10n 的形式，其中 1|a| 10 ，n 为整数，表示时关键要正确确定 a 的值以及 n 的值3（3 分）下列计算正确的是（ ）Aa 4ba2ba 2b B（ab） 2a 2b 2Ca 2a3a 6 D3a 2+2a2a 2【分析】根据各个选项中的式子可以计算出正确的结果，从而可以解答本题【解答】解：a 4ba2ba 2，故选项 A 错误，（ab） 2a 22ab+b 2，故选项 B 错误，a2a3a 5，故选项 C 错误，3a
13、 2+2a2a 2，故选项 D 正确，故选：D【点评】本题考查整式的混合运算，解答本题的关键是明确整式混合运算的计算方法4（3 分）如图，ABEF ，CDEF，BAC50，则ACD（ ）A120 B130 C140 D150【分析】如图，作辅助线；首先运用平行线的性质求出DGC 的度数，借助三角形外角的性质求出ACD 即可解决问题【解答】解：如图，延长 AC 交 EF 于点 G；ABEF，DGCBAC50；CDEF ，CDG90，ACD90+50140，故选：C【点评】该题主要考查了垂线的定义、平行线的性质、三角形的外角性质等几何知识点及其应用问题；解题的方法是作辅助线，将分散的条件集中；解题
14、的关键是灵活运用平行线的性质、三角形的外角性质等几何知识点来分析、判断、解答5（3 分）下列图形是中心对称图形的是（ ）A BC D【分析】根据把一个图形绕某一点旋转 180，如果旋转后的图形能够与原来的图形重合，那么这个图形就叫做中心对称图形可得答案【解答】解：A、不是中心对称图形，故此选项错误；B、不是中心对称图形，故此选项错误；C、不是中心对称图形，故此选项错误；D、是中心对称图形，故此选项正确；故选：D【点评】此题主要考查了中心对称图形，关键是要寻找对称中心，旋转 180 度后两部分重合6（3 分）下列几何体中，同一个几何体的主视图与俯视图不同的是（ ）A B C D【分析】主视图、左
15、视图、俯视图是分别从物体正面、侧面和上面看，所得到的图形【解答】解：A、圆柱的主视图与俯视图都是矩形，错误；B、正方体的主视图与俯视图都是正方形，错误；C、圆锥的主视图是等腰三角形，而俯视图是圆和圆心，正确；D、球体主视图与俯视图都是圆，错误；故选：C【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图，俯视图是从物体的上面看得到的视图7（3 分）不等式组 的解集在数轴上表示正确的是（ ）ABCD【分析】分别解两个不等式得到 x1 和 x3，从而得到不等式组的解集为1x3，然后利用此解集对各选项进行判断【解答】解： ，解得 x1，解得 x3，所以不等式组的解集为1x3故选：C【点评
16、】本题考查了解一元一次不等式组：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到8（3 分）点 P（1，2）关于 y 轴对称的点的坐标是（ ）A（1，2） B（1，2） C（1，2） D（2，1）【分析】关于 y 轴对称的点，纵坐标相同，横坐标互为相反数，可得答案【解答】解：P（1，2）关于 y 轴对称的点的坐标是（1，2），故选：C【点评】本题考查了关于 y 轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：关于 x 轴对称的点，横坐标相同，纵坐标互为相反数
17、；关于 y 轴对称的点，纵坐标相同，横坐标互为相反数；关于原点对称的点，横坐标与纵坐标都互为相反数9（3 分）在 2016 年龙岩市初中体育中考中，随意抽取某校 5 位同学一分钟跳绳的次数分别为：158，160，154，158，170，则由这组数据得到的结论错误的是（ ）A平均数为 160 B中位数为 158C众数为 158 D方差为 20.3【分析】分别利用平均数、中位数、众数及方差的定义求解后即可判断正误【解答】解：A、平均数为（158+160+154+158+170）5160，正确，故本选项不符合题意；B、按照从小到大的顺序排列为 154，158，158，160，170，位于中间位置的数
18、为 158，故中位数为 158，正确，故本选项不符合题意；C、数据 158 出现了 2 次，次数最多，故众数为 158，正确，故本选项不符合题意；D、这组数据的方差是 S2 （154160） 2+2（158160） 2+（160160）2+（170160） 228.8，错误，故本选项符合题意故选：D【点评】本题考查了众数、平均数、中位数及方差，解题的关键是掌握它们的定义，难度不大10（3 分）若 x2 是关于 x 的一元二次方程 x2+ axa 20 的一个根，则 a 的值为（ ）A1 或 4 B1 或4 C1 或4 D1 或 4【分析】把 x2 代入已知方程，列出关于 a 的新方程，通过解新
19、方程可以求得 a 的值【解答】解：根据题意，将 x2 代入方程 x2+ axa 20，得：43aa 20，即 a2+3a40，左边因式分解得：（a1）（a+4）0，a10，或 a+40，解得：a1 或4，故选：C【点评】本题考查了一元二次方程的解的定义能使一元二次方程左右两边相等的未知数的值是一元二次方程的解又因为只含有一个未知数的方程的解也叫做这个方程的根，所以，一元二次方程的解也称为一元二次方程的根11（3 分）甲、乙两人用如图所示的两个转盘（每个转盘被分成面积相等的 3 个扇形）做游戏游戏规则：转动两个转盘各一次，当转盘停止后，指针所在区域的数字之和为偶数时甲获胜；数字之和为奇数时乙获胜
20、若指针落在分界线上，则需要重新转动转盘甲获胜的概率是（ ）A B C D【分析】首先画出树状图，然后计算出数字之和为偶数的情况有 5 种，进而可得答案【解答】解：如图所示：数字之和为偶数的情况有 5 种，因此甲获胜的概率为 ，故选：C【点评】此题主要考查了画树状图和概率，关键是掌握概率所求情况数与总情况数之比12（3 分）如图，在ABC 中，点 D 是 AB 边上的一点，若ACDB，AD1，AC2，ADC 的面积为 1，则BCD 的面积为（ ）A1 B2 C3 D4【分析】由ACDB 结合公共角AA，即可证出ACDABC，根据相似三角形的性质可得出 （ ） 2 ，结合ADC 的面积为 1，即可
21、求出BCD的面积【解答】解：ACDB，AA，ACDABC， （ ） 2 S ACD 1，S ABC 4，S BCD S ABC S ACD 3故选：C【点评】本题考查相似三角形的判定与性质，牢记“相似三角形的面积比等于相似比的平方”是解题的关键13（3 分）如图，以等边三角形 ABC 的 BC 边为直径画半圆，分别交 AB、AC 于点E、D， DF 是圆的切线，过点 F 作 BC 的垂线交 BC 于点 G若 AF 的长为 2，则 FG 的长为（ ）A4 B6 C3 D2【分析】连接 OD，由 DF 为圆的切线，利用切线的性质得到 OD 垂直于 DF，根据三角形 ABC 为等边三角形，利用等边三
22、角形的性质得到三条边相等，三内角相等，都为60，由 ODOC，得到三角形 OCD 为等边三角形，进而得到 OD 平行与 AB，由 O为 BC 的中点，得到 D 为 AC 的中点，在直角三角形 ADF 中，利用 30所对的直角边等于斜边的一半求出 AD 的长，进而求出 AC 的长，即为 AB 的长，由 ABAF 求出 FB的长，在直角三角形 FBG 中，利用 30所对的直角边等于斜边的一半求出 BG 的长，再利用勾股定理即可求出 FG 的长【解答】解：连接 OD，DF 为圆 O 的切线，ODDF ，ABC 为等边三角形，ABBCAC，A B C 60，ODOC，OCD 为等边三角形，CDOA60
23、，ABCDOC 60，ODAB，DFAB，在 Rt AFD 中，ADF30，AF2，AD4，即 AC8，FBABAF826，在 Rt BFG 中，BFG30，BG3，则根据勾股定理得：FG3 故选：C【点评】此题考查了切线的性质，等边三角形的性质，含 30直角三角形的性质，勾股定理，熟练掌握切线的性质是解本题的关键14（3 分）如图，在矩形 AOBC 中，O 为坐标原点，OA、OB 分别在 x 轴、y 轴上，点 B的坐标为（0，3 ）， ABO30，将ABC 沿 AB 所在直线对折后，点 C 落在点D 处，则点 D 的坐标为（ ）A（ ， ） B（2， ） C（ ， ）D（ ，3 ）【分析】根
24、据翻折变换的性质结合锐角三角函数关系得出对应线段长，进而得出 D 点坐标【解答】解：四边形 AOBC 是矩形，ABO30，点 B 的坐标为（0，3 ），ACOB3 ，CAB30，BCACtan303 3，将ABC 沿 AB 所在直线对折后，点 C 落在点 D 处，BAD30，AD 3 ，过点 D 作 DMx 轴于点 M，CABBAD30，DAM30，DM AD ，AM3 cos30 ，MO 3 ，点 D 的坐标为（ ， ）故选：A【点评】此题主要考查了翻折变换以及矩形的性质和锐角三角函数关系，正确得出DAM30是解题关键15（3 分）二次函数 yax 2+bx+c（a、b、c 是常数，且 a0
25、）的图象如图所示，下列结论错误的是（ ）A4acb 2 Babc0 Cb+c3a Dab【分析】根据二次函数的图象与性质即可求出答案【解答】解：（A）由图象可知：0，b 24ac0，b 24ac，故 A 正确；抛物线开口向下，a0，抛物线与 y 轴的负半轴，c0，抛物线对称轴为 x 0，b0，abc0，故 B 正确；当 x1 时，yab+c0，a+cb， 1，a0，b2aa+b+c2b4a，b+ c3a 故 C 正确；当 x1 时yab+c0，ab+cc，ab0，ab，故 D 错误；故选：D【点评】本题考查二次函数图象与性质，解题的关键是熟练运用二次函数的性质，本题属于中等题型，二、填空题（本
26、大题共 5 小题，满分 25 分，只要求填写最后结果，每小题填对得 5 分）16（5 分）将 m3（x2）+m （2x）分解因式的结果是 m（x2）（m1）（m +1） 【分析】先提公因式，再利用平方差公式进行因式分解即可【解答】解：原式m（x2）（m 21）m（x2）（m1）（m+1）故答案为：m（x2）（m 1）（m+1）【点评】本题考查的是多项式的因式分解，掌握提公因式法和平方差公式是解题的关键17（5 分）我国明代数学读本算法统宗一书中有这样一道题：一支竿子一条索，索比竿子长一托，对折索子来量竿，却比竿子短一托如果 1 托为 5 尺，那么索长为 20 尺，竿子长为 15 尺【分析】设索
27、长为 x 尺，竿子长为 y 尺，根据“索比竿子长一托，对折索子来量竿，却比竿子短一托”，即可得出关于 x、y 的二元一次方程组，解之即可得出结论【解答】解：设索长为 x 尺，竿子长为 y 尺，根据题意得： ，解得： 答：索长为 20 尺，竿子长为 15 尺故答案为：20；15【点评】本题考查了二元一次方程组的应用，找准等量关系，正确列出二元一次方程组是解题的关键18（5 分）如图，D 是等边 ABC 边 AB 上的点，AD2，DB 4现将ABC 折叠，使得点 C 与点 D 重合，折痕为 EF，且点 E、F 分别在边 AC 和 BC 上，则 【分析】根据等边三角形的性质、相似三角形的性质得到AE
28、DBDF，根据相似三角形的周长比等于相似比计算即可【解答】解：ABC 是等边三角形，AB C60，ABAC BC 6，由折叠的性质可知，EDFC 60，EC ED，FCFD，AEDBDF，AEDBDF， ， ，故答案为： 【点评】本题考查的是翻转变换的性质、相似三角形的判定和性质，掌握相似三角形的判定定理和性质定理、翻转变换的性质是解题的关键19（5 分）如图，RtABC 中，C90，BC15，tanA ，则 AB 17 【分析】根据A 的正切求出 AC，再利用勾股定理列式计算即可得解【解答】解：RtABC 中，C90，tan A ，BC15， ，解得 AC8，根据勾股定理得，AB 17故答案
29、为：17【点评】本题考查了解直角三角形，勾股定理，主要利用了锐角的正切等于对边比邻边20（5 分）如图，过原点 O 的直线与反比例函数 y1，y 2 的图象在第一象限内分别交于点A，B ，且 A 为 OB 的中点，若函数 y1 ，则 y2 与 x 的函数表达式是 y 2 【分析】过 A 作 ACx 轴于 C，过 B 作 BDx 轴于 D，由于点 A 在反比例函数 y1上，设 A（a， ），求得点 B 的坐标代入反比例函数的解析式即可求出结果【解答】解：过 A 作 ACx 轴于 C，过 B 作 BDx 轴于 D，点 A 在反比例函数 y1 上，设 A（a， ），OCa，AC ，ACx 轴，BDx
30、 轴，ACBD，OACOBD， ，A 为 OB 的中点， ，BD2AC ，OD2OC2a，B（2a， ），设 y2 ，k2a 4，y 2 与 x 的函数表达式是：y 2 故答案为：y 2 【点评】本题主要考查了待定系数法求反比例函数，相似三角形的判定和性质，反比例函数 中 k 的几何意义要注意数形结合思想的运用三、解答题（本大题共 7 小题，满分 80 分.解答应写出必要的文字说明、证明过程或推演步骤）21（8 分）计算：（2） 3+ 2sin30+（2016） 0【分析】原式利用乘方的意义，算术平方根定义，特殊角的三角函数值，以及零指数幂法则计算即可得到结果【解答】解：原式8+41+14【点
31、评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键22（8 分）先化简 （ x+1），然后从 x 的范围内选取一个合适的整数作为 x 的值代入求值【分析】根据分式的减法和除法可以化简题目中的式子，然后在 x 中选取一个使得原分式有意义的整数值代入化简后的式子即可解答本题【解答】解： （ x+1） ， x 且 x+10，x10，x0，x 是整数，x2 时，原式 【点评】本题考查分式的化简求值、估算无理数的大小，解答本题的关键是明确分式化简求值的方法，注意取得的 x 的值必须使得原分式有意义23（10 分）五月初，我市多地遭遇了持续强降雨的恶劣天气，造成部分地区出现严重洪涝灾害，某爱心组织紧
32、急筹集了部分资金，计划购买甲、乙两种救灾物品共 2000 件送往灾区，已知每件甲种物品的价格比每件乙种物品的价格贵 10 元，用 350 元购买甲种物品的件数恰好与用 300 元购买乙种物品的件数相同（1）求甲、乙两种救灾物品每件的价格各是多少元？（2）经调查，灾区对乙种物品件数的需求量是甲种物品件数的 3 倍，若该爱心组织按照此需求的比例购买这 2000 件物品，需筹集资金多少元？【分析】（1）设每件乙种物品的价格是 x 元，则每件甲种物品的价格是（x+10）元，根据用 350 元购买甲种物品的件数恰好与用 300 元购买乙种物品的件数相同列出方程，求解即可；（2）设甲种物品件数为 m 件，
33、则乙种物品件数为 3m 件，根据该爱心组织按照此需求的比例购买这 2000 件物品列出方程，求解即可【解答】解：（1）设每件乙种物品的价格是 x 元，则每件甲种物品的价格是（x+10）元，根据题意得， ，解得：x60经检验，x60 是原方程的解，x+1060+1070答：甲、乙两种救灾物品每件的价格各是 70 元、60 元；（2）设甲种物品件数为 m 件，则乙种物品件数为 3m 件，根据题意得，m+3m2000，解得 m500，即甲种物品件数为 500 件，则乙种物品件数为 1500 件，此时需筹集资金：70500+601500125000（元）答：若该爱心组织按照此需求的比例购买这 2000
34、 件物品，需筹集资金 125000 元【点评】本题考查分式方程、一元一次方程的应用，分析题意，找到合适的等量关系是解决问题的关键24（12 分）某学校为调查学生的兴趣爱好，抽查了部分学生，并制作了如下表格与条形统计图：频数 频率体育 40 0.4科技 25 a艺术 b 0.15其它 20 0.2请根据上图完成下面题目：（1）总人数为 100 人，a 0.25 ，b 15 （2）请你补全条形统计图（3）若全校有 600 人，请你估算一下全校喜欢艺术类学生的人数有多少？【分析】（1）根据“频率频数总数”求解可得；（2）根据频数分布表即可补全条形图；（3）用总人数乘以样本中“艺术”类频率即可得【解答
35、】解：（1）总人数为 400.4100 人，a251000.25、b1000.1515，故答案为：100、0.25、15；（2）补全条形图如下：（3）估算全校喜欢艺术类学生的人数有 6000.1590 人【点评】此题主要考查了条形统计图的应用以及利用样本估计总体，根据题意求出样本总人数是解题关键25（12 分）已知正方形 ABCD，P 为射线 AB 上的一点，以 BP 为边作正方形 BPEF，使点 F 在线段 CB 的延长线上，连接 EA、EC （1）如图 1，若点 P 在线段 AB 的延长线上，求证：EAEC；（2）若点 P 在线段 AB 上如图 2，连接 AC，当 P 为 AB 的中点时，
36、判断ACE 的形状，并说明理由；如图 3，设 ABa，BPb，当 EP 平分AEC 时，求 a：b 及AEC 的度数【分析】（1）根据正方形的性质和全等三角形的判定定理证明APECFE，根据全等三角形的性质证明结论；（2） 根据正方形的性质、等腰直角三角形的性质解答；根据 PECF ，得到 ，代入 a、b 的值计算求出 a：b，根据角平分线的判定定理得到HCGBCG，证明AECACB，即可求出AEC 的度数【解答】解：（1）四边形 ABCD 和四边形 BPEF 是正方形，ABBC，BPBF，APCF，在APE 和CFE 中，APE CFE，EAEC；（2） P 为 AB 的中点，PAPB，又
37、PBPE ，PAPE，PAE 45，又DAC45，CAE90，即ACE 是直角三角形；EP 平分AEC，EPAG，APPG ab，BGa （2a2b）2baPECF， ，即 ，解得，a b；作 GHAC 于 H，CAB45，HG AG （2 b2b）（2 ）b，又 BG2ba（2 ）b，GHGB ，GH AC，GB BC，HCGBCG，PECF，PEGBCG，AECACB45a：b ：1；AEC45【点评】本题考查的是正方形的性质、直角三角形的判定、相似三角形的判定和性质以及等腰直角三角形的性质，掌握相关的性质定理和判定定理、正确作出辅助性是解题的关键26（14 分）如图，在ABC 中，C90
38、，BAC 的平分线交 BC 于点 D，点 O 在AB 上，以点 O 为圆心，OA 为半径的圆恰好经过点 D，分别交 AC，AB 于点 E，F（1）试判断直线 BC 与O 的位置关系，并说明理由；（2）若 BD2 ，BF2，求阴影部分的面积（结果保留 ）【分析】（1）连接 OD，证明 ODAC，即可证得ODB90，从而证得 BC 是圆的切线；（2）在直角三角形 OBD 中，设 OFODx ，利用勾股定理列出关于 x 的方程，求出方程的解得到 x 的值，即为圆的半径，求出圆心角的度数，直角三角形 ODB 的面积减去扇形 DOF 面积即可确定出阴影部分面积【解答】解：（1）BC 与O 相切证明：连接
39、 ODAD 是BAC 的平分线，BADCAD又ODOA ，OAD ODACADODAODACODB C90，即 ODBC 又BC 过半径 OD 的外端点 D，BC 与O 相切（2）设 OFODx，则 OBOF+BFx+2，根据勾股定理得：OB 2OD 2+BD2，即（x+2） 2x 2+12，解得：x2，即 ODOF2，OB2+2 4，RtODB 中，OD OB，B30，DOB 60 ，S 扇形 DOF ，则阴影部分的面积为 SODB S 扇形 DOF 22 2 故阴影部分的面积为 2 【点评】本题考查了切线的判定，扇形面积，以及勾股定理，熟练掌握切线的判定是解本题的关键27（16 分）如图，
40、对称轴为直线 x2 的抛物线 yx 2+bx+c 与 x 轴交于点 A 和点 B，与y 轴交于点 C，且点 A 的坐标为（ 1，0）（1）求抛物线的解析式；（2）直接写出 B、C 两点的坐标；（3）求过 O，B，C 三点的圆的面积（结果用含 的代数式表示）注：二次函数 yax 2+bx+c（ a0）的顶点坐标为（ ， ）【分析】（1）利用对称轴方程可求得 b，把点 A 的坐标代入可求得 c，可求得抛物线的解析式；（2）根据 A、B 关于对称轴对称可求得点 B 的坐标，利用抛物线的解析式可求得 B 点坐标；（3）根据 B、C 坐标可求得 BC 长度，由条件可知 BC 为过 O、B 、C 三点的圆
41、的直径，可求得圆的面积【解答】解：（1）由 A（1，0），对称轴为 x2，可得 ，解得 ，抛物线解析式为 yx 24x5；（2）由 A 点坐标为（1，0），且对称轴方程为 x2，可知 AB6，OB5，B 点坐标为（5，0），yx 24x 5，C 点坐标为（0，5）；（3）如图，连接 BC，则OBC 是直角三角形，过 O、B、C 三点的圆的直径是线段 BC 的长度，在 Rt OBC 中， OBOC5，BC5 ，圆的半径为 ，圆的面积为 （ ） 2 【点评】本题为二次函数的综合应用，涉及知识点有二次函数的性质、待定系数法、勾股定理、圆周角定理等在（3）中确定出圆的半径是解题的关键本题属于基础性的题目，难度不大
