1、高三校际联合考试理科数学2019.05本试卷共 6 页，满分 150 分。考生注意：1答题前，考生务必将自己的准考证号、姓名填写在答题卡上。考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致。2。回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。如需改动，用橡皮擦干净后，再选涂其他答案标号。回答非选择题时，将答案写在答题卡上。写在本试卷上无效。3考试结束，监考员将试题卷、答题卡一并收回。参考公式：锥体体积 ，(S 为锥体底面面积，h 为锥体高)1=3VS锥一、选择题：本大题共 12 小题，每小题 5 分，共 60 分。在每小题
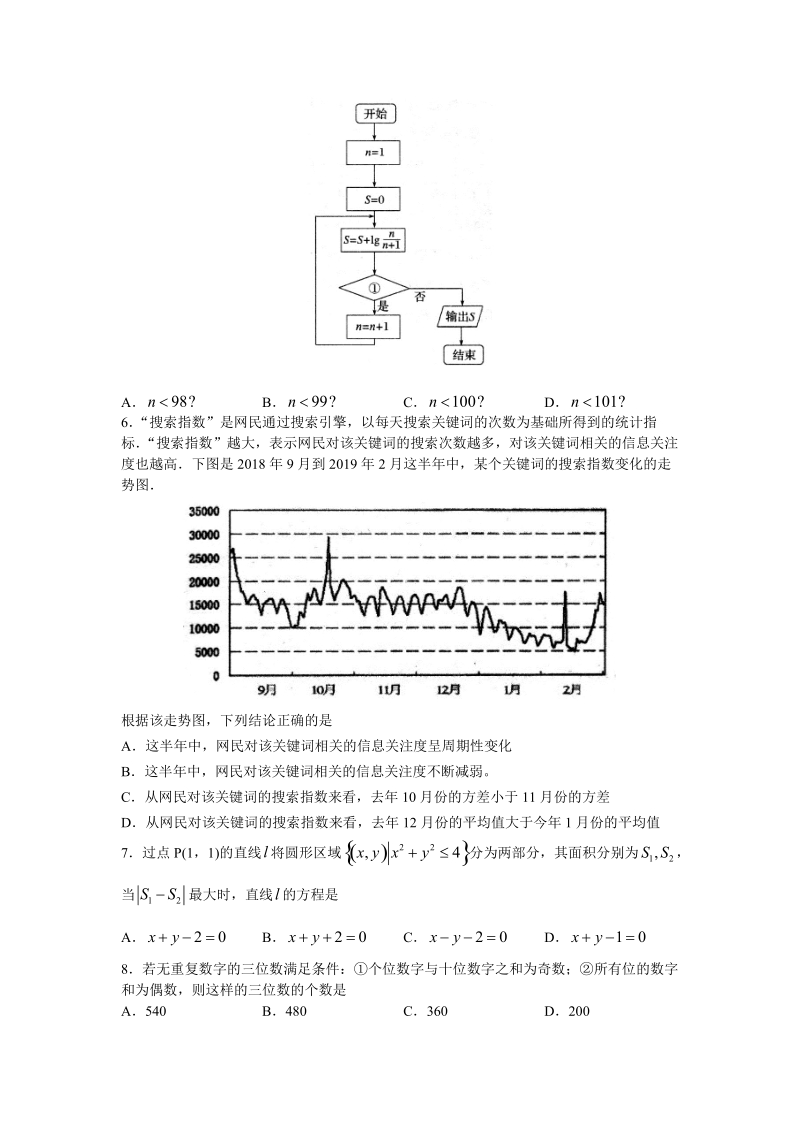
2、给出的四个选项中，只有一项是符合题目要求的。1已知集合 ，则10,1AxgBxA B C DRBAB2将函数 f(x)=sin2x 的图象向右平移 个单位长度得到 图象，则函数的解析式是6gxA Bsin23gsin26gxC Dixi3若函数 3log2,03xf f， 则A B C D014已知 m，n 是两条不同的直线， 是两个不同的平面，给出四个命题：,若 ； 若 ；,则 ,/m则若 ； 若 .则 /n则其中正确的是A B C D5执行如图所示的程序框图，若输出的 S 值为 ，则中应填2A B C D98?n9?n10?n10?n6 “搜索指数”是网民通过搜索引擎，以每天搜索关键词的次
3、数为基础所得到的统计指标 “搜索指数”越大，表示网民对该关键词的搜索次数越多，对该关键词相关的信息关注度也越高下图是 2018 年 9 月到 2019 年 2 月这半年中，某个关键词的搜索指数变化的走势图根据该走势图，下列结论正确的是A这半年中，网民对该关键词相关的信息关注度呈周期性变化B这半年中，网民对该关键词相关的信息关注度不断减弱。C从网民对该关键词的搜索指数来看，去年 10 月份的方差小于 11 月份的方差D从网民对该关键词的搜索指数来看，去年 12 月份的平均值大于今年 1 月份的平均值7过点 P(1，1)的直线 将圆形区域 分为两部分，其面积分别为 ，l2,4xy12,S当 最大时
4、，直线 的方程是12SA B C D0xy20xy20xy0xy8若无重复数字的三位数满足条件：个位数字与十位数字之和为奇数；所有位的数字和为偶数，则这样的三位数的个数是A540 B480 C360 D2009倾斜角为 30的直线 经过双曲线 的左焦点 F1，交双曲线于l 210,xyabA，B 两点，线段 AB 的垂直平分线过右焦点 E，则此双曲线的渐近线方程为A B C Dyx12yx32yx52yx10已知点 A，B，C，D 在同一个球的球面上， ，若四面体,ABCABCD 外接球的球心 O 恰好在侧棱 DA 上， ，则四面体 ABCD 的体积为3DA B C D3322311已知数列
5、前 n 项和为 ，满 ( 为常数) ，且 ，设函数anS2abn,92a，则数列 的前 17 项和为22sii,nxfxyf记 yA B C11 D1717912设函数 ，若函数 有三1,2log,1axf xa2gxfbfxc个零点 ，则123,x1231A12 B11 C6 D3二、填空题：本大题共 4 小题，每小题 5 分，共 20 分。13设复数 (i 为虚数单位)，则 z 的虚部是 _5zi14设向量 ，则向量 与向量 a 的夹角为_1,2abb15抛物线 图象在第一象限内一点 处的切线与 轴交点的横坐标记为 ，2yx2i x1ia其中 iN *，若 ，则 _23246a16若函数
6、(e 为自然对数的底数) 在 两处取得极值，且1xfxme12x和，则实数 m 的取值范围是 _21x三、解答题：共 70 分。解答应写出文字说明，证明过程或演算步骤。第 1721 题为必考题。每个试题考生都必须作答。第 22、23 题为选考题，考生根据要求作答。17(12 分)如图，在 中，M 是 AC 的中点， ABC,23CAM(1)若 ，求 AB 的长；512A(2)若 的面积3,BMBC求18(12 分)在如图所示的几何体中，四边形 ABCD 是边长为 2 的菱形，平面DEABCD，BF/DE，DE=2BF= 260DAB，(1)证明：平面 平面 BDEF；ACF(2)求二面角 EA
7、CF 的余弦值19(12 分)如图，已知椭圆 ， 是长轴的一个端点，弦 BC 过椭圆的210xyab： 4,A中心 O，且 3cos,2ACOBC(1)求椭圆 E 的方程。(2)过椭圆 E 右焦点 F 的直线，交椭圆 E 于 两点，交直线1,A于点 M判定直线 的斜率是否依次构成等8x1,B差数列?请说明理由20(12 分)为评估设备 M 生产某种零件的性能，从设备 M 生产零件的流水线上随机抽取 100 个零件作为样本，测量其直径后，整理得到下表：经计算，样本的平均值 ，标准差 ，以频率值作为概率的估计值64u2.(1)为评判一台设备的性能，从该设备加工的零件中任意抽取一件，记其直径为 X，
8、并根据以下不等式进行评判(P 表示相应事件的频率)： ； ；0.8PuX20.954PuXu 33974u评判规则为：若同时满足上述三个不等式，则设备性能等级为甲；仅满足其中两个，则设备性能等级为乙；若仅满足其中一个，则设备性能等级为丙；若全部不满足，则设备性能等级为丁试判断设备 M 的性能等级(2)将直径小于等于 或直径大于 的零件认为是次品2u2u(i)从设备 M 的生产流水线上任意抽取 2 个零件，计算其中次品个数 Y 的数学期望 ； EY(ii)从样本中任意抽取 2 个零件，计算其中次品个数 Z 的数学期望 E(Z)21(12 分)已知函数 (e 为自然对数的底数 )sin,0,2xf
9、e(1)求函数 的值域；f(2)若不等式 对任意 恒成立，求实数 k 的取值范围；1sinfxkx0,2(3)证明： .213xe请考生在第 22、23 两题中任选一题作答，如果多做，则按所做的第一题计分。22(10 分) 选修 4-4：坐标系与参数方程在直角坐标系 中，直线 的参数方程是 (t 为参数)，曲线 C 的参数方程xoylcos31inxty是 ( 为参数) 以 O 为极点，x 轴的非负半轴为极轴建立极坐标23csiny系(1)求直线 和曲线 C 的极坐标方程；l(2)已知射线 与曲线 C 交于 O， M 两点，射线 与1:02OM 2:N直线 交于 N 点，若OMN 的面积为 1
10、，求 的值和弦长 .l 23(10 分) 选修 4-5：不等式选讲已知函数 ,fxaR(1)若 的取值范围；1求(2)若 ，不等式 恒成立，求 的取值范0,axya， 对 342afxya围。绝密启用前 试卷类型：A高三校际联合考试理科数学答案 2019.051、选择题：本大题共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有一项是符合题目要求的。1-5 BCBBB 6-10 DADAC 11-12 DB1.答案 B解析：由 且 ， ,故选 B.|1,x|lg01AxxAR2.答案 C解析：由题意，将函数 的图象向右平移 个单位长度，sin2fx6可得 ，故选 Csi
11、n2()i()63gx3.答案 B解析：由题意得 ，因此 ，故选 B.3()1f3()(1log2ff4.答案 B解析: 两个平面斜交时也会出现一个平面内的直线垂直于两个平面的交线的情况，不正确；垂直于同一条直线的两个平面平行，正确；当两个平面与两条互相垂直的直线分别垂直时，它们所成的二面角为直二面角，故正确；当两个平面相交时，分别与两个平面平行的直线也平行，故不正确.故选 B5.答案 B解析: 由题意知，该程序框图的功能是计算 ，12lglgl(1)3nS当 时， ；当 时， ，跳出循环，故中应填=98nlg92S=9n0=，故选 B.?6.答案 D解析：选项 A 错，并无周期变化；选项 B
12、 错，并不是不断减弱，中间有增强；选项 C 错，月的波动大于 月份，所以方差要大；选项 D 对，由图可知， 月起到 月份有下降101 12的趋势，所以会比 月份大.故选 D.7. 答案 A 解析：当圆心 与 的连线和过点 的直线垂直时，符合条件.圆心 与点 连线的斜率OPOP，所以直线 的方程为 .故选 A.1=kl20xy8.答案 D解析：由题意知，这个三位数的百位一定是奇数，其所有取法有 种；其个位数字与5=1C十位数字是一奇一偶，其所有取法种数有 种，由分步计数原理可知，这402154AC样的三位数共有 个，故选.D20=459.答案 A解析：如图 为 的垂直平分线，可得 ，2MF2B2
13、FB且 ，可得 ，30=1 sin30c，由双曲线的定义可得cos， ，12BFa21AFa即有 ，1 2()4BAFa即有 ，222 +=+=cM,aM132AFMca由 ，可得 ，21AF4(3)aca可得 ，即 ， ，则渐近线方程为 ，故选23+4c2bxy=A10.答案 C解析：由 可知 ，取 的中点 ，则点 为,AC,B2=2=BACM外接圆的圆心，所以 平面 ，且 为 的中位线，所以AOMOD平面 故三棱锥 的体积为 .故选 C.DCD12332V11.答案 D解析： ,()sin2cos1fxx由 ，得 ， 为等差数列， + = ,2=nSab=abna1a792+ = +17y
14、1()fa7f11sin2cosa1717in2cosa= + =sin2cos()()数列 的前 项和为 = .故选 D.y812.答案 B解析：作出函数 的图象如图所示，由图可得关于 的方程()fxx的解有两个或三个( 时有三个， 时有两个)，所以)fxt1t1t关于 的方程 只能有一个根 (若有两个根，则关20btc于 的方程 有四个或五个根)，由 ，()fxf )1fx可得 的值分别为 ， .故选 B123,1,3123123x2、填空题：本大题共 4 小题，每小题 5 分，共 20 分。13. 14. (或 ) 15. 16. 454,ln213.答案 解析： .=(i)16iz14
15、.答案 (或 ) 45解析： ， ， .0,3ab32cos415.答案 42解析： ， ， 在第一象限内图象上(0)yx4yx2(0)yx一点 ， 处的切线方程是： ，整理，得 ，(ia2i iiia 240iiaxy切线与 轴交点的横坐标为 ， ， 是首项为 ，公比 的等x1i12ii2ka2314q比数列， 2463284a16.答案 1,ln2解析：方法 1： ， ， ，直线 ，曲线 ，()2exfxm1=x2exmymxy=ex，2A（ ， ） ，B（ ， ） ，1x41x12e， ，2eln构造 ， ，在（0,1）递减，()xg2e)()x（.e1(ln2)xm方法 2：()exf
16、x由题知 有两个不等的实数根 ， 且 ，2m1x21x令 ，则 ，()xh2()xh易知 在 ， 上为减函数；在 上为增函数.,0(,(,)当 时，由 ，得 ，此时 ；21x12ex1ln2x1ln2m当 时,21lnm综上 .l， +三、解答题：17.解:(1) , 2 分53124ABC在 中，由正弦定理得 ,sinsiACB. 6 分sin=26si4AB(2)在 中，由余弦定理得CM2cos3C，21=+2CMBCA，14解得 (负值舍去)， 10 分， 12 分sin432ABCS18.解: (1)连接 交 于点 ，因为 是菱形,DAOABCD所以 ，平面 ，E, 3 分C又 平面
17、,BF平面 ,D,E平面 ,ACBF平面 平面 . 5 分D(2)连接 交 于点 ，则 ,OACB取 的中点 ，连接 ，则 ,EG/GE平面 ，AB平面 ，OD两两垂直.,C以 所在直线分别作为 轴， 轴， 轴建立空间直角坐标系(如图)，则ABGxyz, , , , ,(30)(1)(30)1012)E(01,2)F, ,2E2AC,(0,2)E(3,12)AF, (,)CF则 , ，00F所以 ， ，且 ，EACAF所以 平面 ，所以平面 的一个法向量为 . 9 分F(0,2)E设平面 的一个法向量为 ，则AEC(,)xyzn=,0n,320xyz得 ，x令 ，2z得平面 的一个法向量 ，A
18、EC=(0,42)n从而 63|Fcosn,由观察知二面角 为锐角，故所求的二面角 的余弦值为 . 12 分EACF319.解：（1）又 即 ，2,OBA2BC 是等腰三角形 ， 2 分 ， ，13cos,AC 13cosO ， , 3 分(4,0)42,Cxy(2)点 C 在椭圆上， ，291,4ab1b所求椭圆方程为 . 5 分6xy（2）因为 , ,(0)F23由题意可知直线 的斜率存在，设直线 的的方程为 ，ll(2)ykx令 ，得 的坐标为 8xM(8,6)k由 ，得 . 7 分216()ykx222(43)16(3)0xk设 ，则有 9 分112(,)(,)AxyB2212166(
19、3),434kkxx设直线 的斜率分别为 ，1,CM12,从而 21 336,8ykkx因为直线 的方程为 ，所以 ，1AB()yx12(),()ykxykx所以 2121 12()33kxk 21143()xx把代入，得 21222164331()4kk k又 ，所以 ，3k123k故直线 的斜率成等差数列 12 分1,CAMB20.解:（1） ()(61.8.2)08.62PuXPX(2259.4954，33)(70.).7因为设备 的数据仅满足一个不等式，故其性能等级为丙； 5 分M（2）易知样本中次品共 6 件，可估计设备 生产零件的次品率为 0.06.M（）由题意可知 ，于是 ， 8
20、 分(2,0.)YB:()20.6.1EY（）由题意可知 的分布列为ZZ 0 1 2P29410C694210 6210C故 . 12 分2129469462100103() 5CCEZ21.解：（1） ()e(sinco)xf xe12(si)4xx2inx， ， ，所以 ，故函数0,2xQ3,4si()4x()0fx在 上单调递减，故函数 的最大值为 ； 的最()f, f 0(esin1f()fx小值为 ，所以函数 的值域为 . 3 分2esin0f)fx,(2)原不等式可化为 .(*)，(1i)(1sinxk因为 恒成立，故（*）式可化为 .1sin0e(1)xk令 ，则()exgk()
21、xg当 时， ，所以函数 在 上单调递增，故k()0x()g0,2，所以 ；()01xk1k当 时，令 ，得 ，且当 时，k()exglnx(,ln)xk； 当 时， .()exg(ln,)k()e0g所以当 即 时，函数 ，ln,2k20eminl)2ln(2l)0xkk成立；当 即 时，函数 在 上单调递减，l,k2e()gx0,2，解得2min()()e0gxk22e1k综上， . 9 分21k(3)法一：令 则 .123()e()1,xh13()e2xh由 ，故存在 ，使得 即1124()e0,()e00(,)4x0()hx.且当 时， ；当 时， .故当0103x0(,)x()h0(
22、,)()时，函数 有极小值，且是唯一的极小值，故函数0)h012min03()(e()1xhx，因为 ，22200 033153)()2xx013(,)24x所以 ，2015135()(4x故 12 分12()e()0,xh123e()1x法二：证明123()x令 当 时， ；当 时，11()e,)e,xxuu(,1)()0ux(1,).故当且仅当 时，函数 有极小值，且是唯一的极小值，故函数0u,即 ，当且仅当 时取等号；min()(1)x1exx令 所以22 2311()08v x当 时取等号.故 .21()1xx123e()x22.解：（1）直线 l 的参数方程是 （ 为参数） ，cos
23、31inxtyt消去参数 得直角坐标方程为： t 0x转换为极坐标方程为： ，即 3cosin11sin()32曲线 的参数方程是 （ 为参数） ，C2sixy转换为直角坐标方程为： ， 3 分22(3)1化为一般式得 240xy化为极坐标方程为： 5 分sin（2）由于 ，得 ，023OM11cosinsin()3cos()2ON所以 ，1i12cs3nOMNSV所以 ，3tan由于 ，所以 ，026所以 10 分3OM23.（10 分）解：（1） ，()11fa若 ，则 ，得 ，即不等式无解，a2若 ，则 ，得 ，即 ，1a若 ，则 ，得 ，即不等式恒成立，11a综上所述， 的取值范围是 5 分a1(,)2（2）由题意知，要使得不等式恒成立，只需 ，maxmin3()42afy当 时， ，所以 (,xa()fxaax()()ff因为 ，33424y所以 ，解得 ，结合 ，2a1a0所以 的取值范围是 10 分3,0)
