1、精选大题2019朝阳期末如图，三棱柱 的侧面 是平行四边形， ，平面1ABC1BC1BC平面 ，且 ， 分别是 ， 的中点1AC1BEFA（1）求证： ；1BCA（2）求证： 平面 ；/EF1（3）在线段 上是否存在点 ，使得 平面 ？若存在，求出 的值；若不存在，请P1BCEFPAPB说明理由【答案】 （1）详见解析；（2）详见解析；（3）当点 是线段 的中点时， 平面 此1CEFP时， APB【解析】 （1） ，又平面 平面 ，且平面 平面 ，1C1AC1B1A1B 平面 A又 平面 ， 111B（2）取 中点 ，连 ，连 CGFC在 中， ， 分别是 ， 中点， ，且 1AB 1A11F
2、GBC 12BC在平行四边形 中， 是 的中点， ，且 1EBE平行、垂直关系证明大题精做六 ，且 四边形 是平行四边形 /ECFGFECG/FEGC又 平面 ， 平面 ， 平面 1A1A/1A（3）在线段 上存在点 ，使得 平面 ABP1BCEFP取 的中点 ，连 ，连 EF 平面 ， 平面 ， 平面 ， ， 1C11AG1AC1BAC1G在 中， ， 分别是 ， 中点， AB PBC/PE又由（2）知 ， ， /FEG1PE1F由 得 平面 CF故当点 是线段 的中点时， 平面 此时， PAB1 12APB模拟精做12019无锡期末在四棱锥 中，锐角三角形 所在平面垂直于平面 ，PABCD
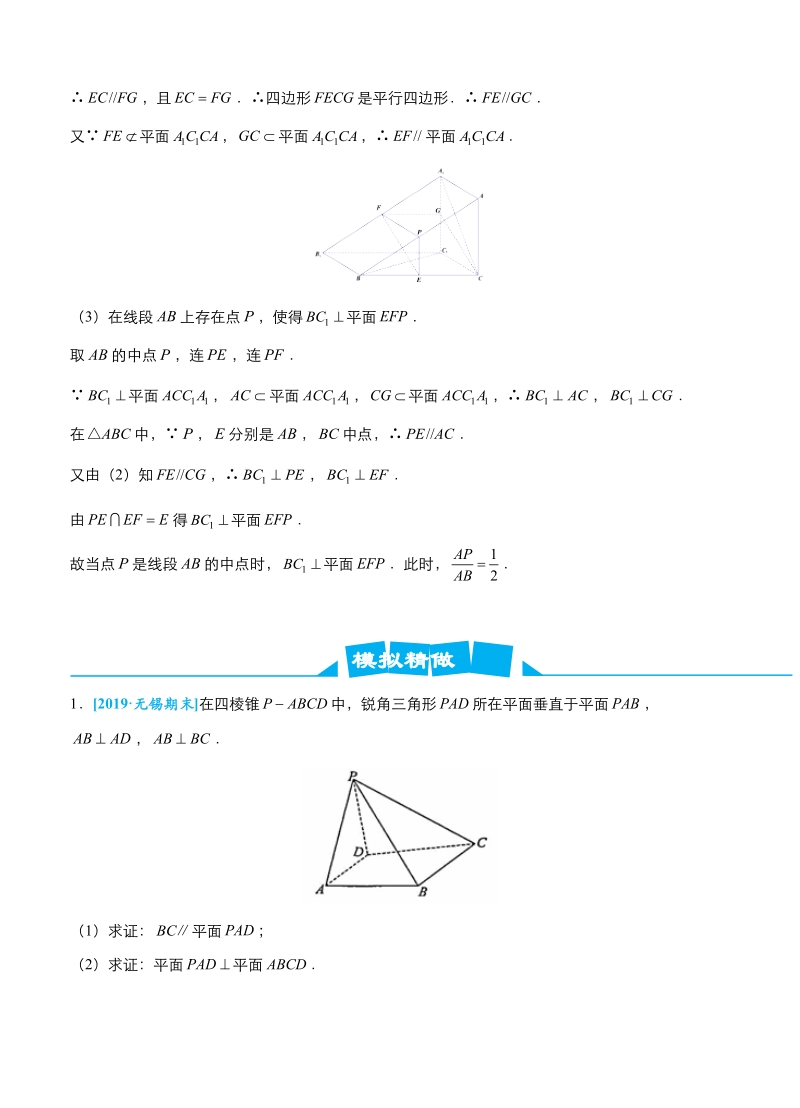
3、PADPAB， ABDB（1）求证： 平面 ；BC PAD（2）求证：平面 平面 BC22019海淀期末在四棱锥 中，平面 平面 ，底面 为梯形，PABCDABCPDABC， ABCD （1）求证： 平面 ；AB PCD（2）求证： 平面 ；（3）若 是棱 的中点，求证：对于棱 上任意一点 ， 与 都不平行MBCFMPC32019大连期末如图，直角梯形 与等腰直角三角形 所在的平面互相垂直ABCDABE， ， ， 2AEBCD 2（1）求证： ；ABDE（2）求证：平面 平面 ；BC（3）线段 上是否存在点 ，使 平面 ？若存在，求出 的值；若不存在，说明理FE FBDEFA由答案与解析1 【
4、答案】 （1）见解析；（2）见解析【解析】 （1）四边形 中， ， ，ABCDABC ， 在平面 外， 平面 BC P PD（2）作 于 ，E平面 平面 ，而平面 平面 ，PADBPADBPA 平面 ， ，EE又 ， ， 平面 ，又 在平面 内，平面 平面 ABCPABC2 【答案】 （1）见证明；（2）见证明；（3）见证明【解析】 （1） ， 平面 ， 平面 ， 平面 D DPDAB PCD（2）法一：平面 平面，平面 平面 ，ABCABCC， 平面 ， 平面 ADC法二：在平面 中过点 作 ，交 于 ，PHPH平面 平面，平面 平面 ， 平面 ，BABCDCDPCD 平面 ，H 平面 ，
5、，AD又 ， ， 平面 PCHAPC（3）法一：假设存在棱 上点 ，使得 ，BCFMPC连接 ，取其中点 ，ACN在 中， ， 分别为 ， 的中点， ，P MPAN过直线外一点只有一条直线和已知直线平行， 与 重合，F点 在线段 上， 是 ， 的交点 ，FAFCB即 就是 ，而 与 相交，矛盾，CP假设错误，问题得证法二：假设存在棱 上点 ，使得 ，显然 与点 不同 ，BFM FC ， ， ， 四点在同一个平面 中，PM ， ， ， ，FCCAP 就是点 ， ， 确定的平面 ，且 ，ABBD这与 为四棱锥矛盾，假设错误，问题得证PD3 【答案】 （1）详见解析；（2）详见解析；（3）存在点 ，
6、且 时，有 平面 F13EAC FBD【解析】 （1）证明：取 中点 ，连结 ， 由等腰直角三角形 可得，ABOEOB ， ， ，EBE四边形 为直角梯形， ， ，CD2CDBAC四边形 为正方形， ， ， 平面 ，OAEBODE ABE（2）平面 平面 ，平面 平面 ，且 ，ABECDABECDABC 平面 ， ，C又 ， ， 平面 ， 平面 ，E平面 平面 AEDBC（3）解：存在点 ，且 时，有 平面 ，连 交 于 ，F13EAC FBDACBM四边形 为直角梯形， ， ，212M又 ， ， ，12EFACMFE 平面 ， 平面 ，BDBD 平面 即存在点 ，且 时，有 平面 13FAEC FBD
