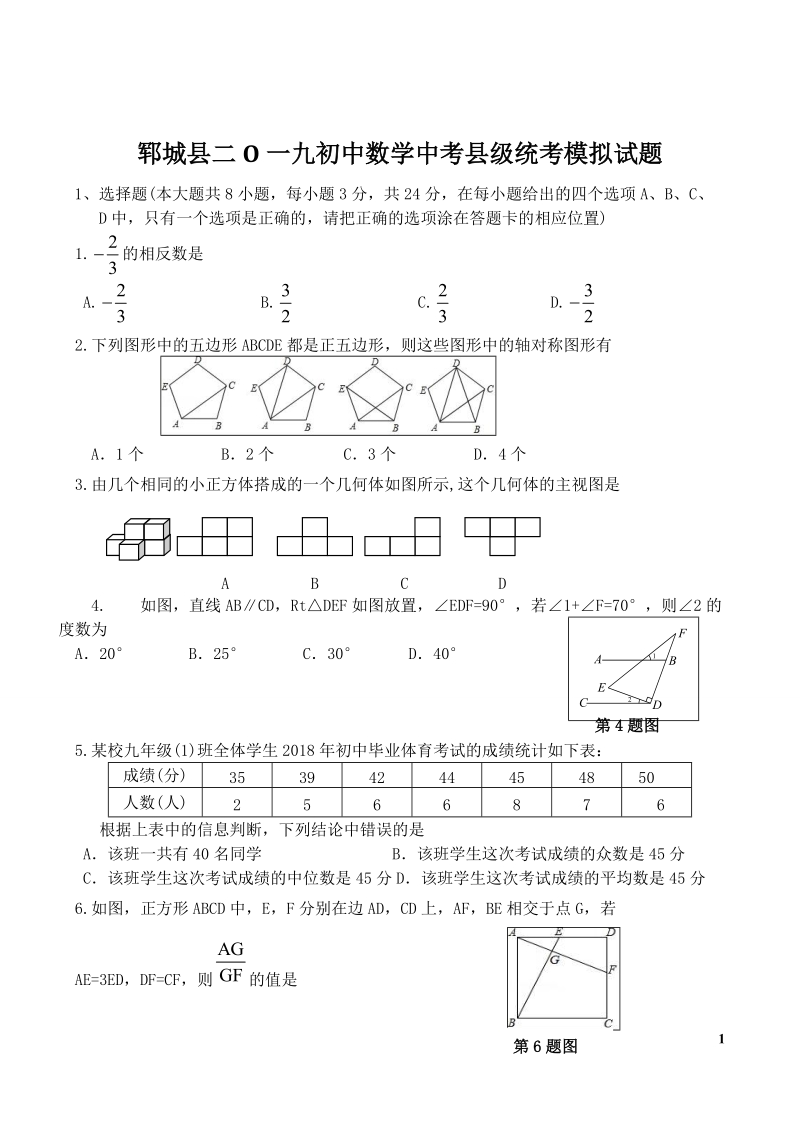
1、1郓城县二 O 一九初中数学中考县级统考模拟试题1、选择题(本大题共 8 小题，每小题 3 分，共 24 分，在每小题给出的四个选项 A、B、C、 D 中，只有一个选项是正确的，请把正确的选项涂在答题卡的相应位置)1. 的相反数是23A. B. C.D.223322.下列图形中的五边形 ABCDE 都是正五边形，则这些图形中的轴对称图形有A1 个 B2 个 C3 个 D4 个3.由几个相同的小正方体搭成的一个几何体如图所示,这个几何体的主视图是 A B C D4. 如图，直线 ABCD，RtDEF 如图放置，EDF=90，若1+F=70，则2 的度数为A20 B25 C30 D40 5.某校九
2、年级(1)班全体学生 2018 年初中毕业体育考试的成绩统计如下表：成绩(分) 35 39 42 44 45 48 50人数(人) 2 5 6 6 8 7 6根据上表中的信息判断，下列结论中错误的是A该班一共有 40 名同学 B该班学生这次考试成绩的众数是 45 分C该班学生这次考试成绩的中位数是 45 分 D该班学生这次考试成绩的平均数是 45 分6.如图，正方形 ABCD 中，E，F 分别在边 AD，CD 上，AF，BE 相交于点 G，若AE=3ED，DF=CF，则 的值是G第 4 题图EDFB21CA第 6 题图2A B C D435465767. 如图，A，B 是反比例函数 在第一象限
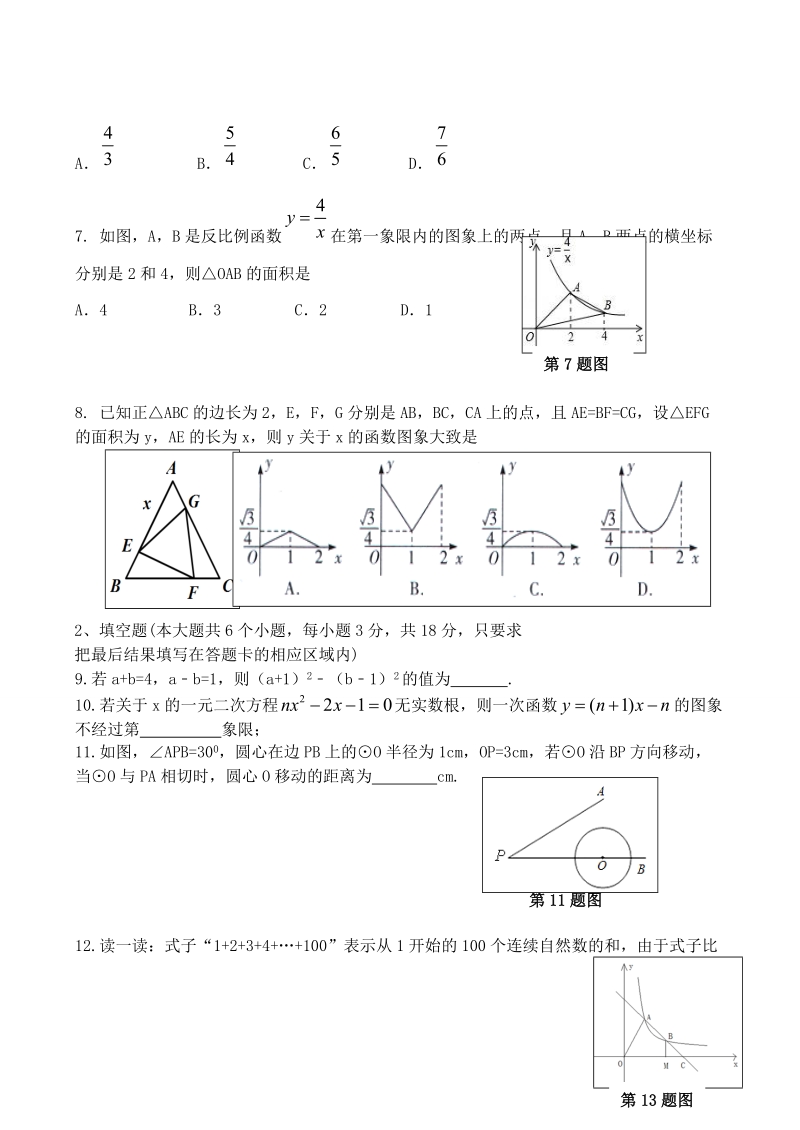
3、内的图象上的两点，且 A，B 两点的横坐标yx分别是 2 和 4，则OAB 的面积是 A4 B3 C2 D18. 已知正ABC 的边长为 2，E，F，G 分别是 AB，BC，CA 上的点，且 AE=BF=CG，设EFG的面积为 y，AE 的长为 x，则 y 关于 x 的函数图象大致是2、填空题(本大题共 6 个小题，每小题 3 分，共 18 分，只要求把最后结果填写在答题卡的相应区域内)9.若 a+b=4，ab=1，则（a+1） 2（b1） 2的值为 .10.若关于 x 的一元二次方程 10nx无实数根，则一次函数 (1)ynx的图象不经过第 象限；11.如图，APB=30 0，圆心在边 PB
4、 上的O 半径为 1cm，OP=3cm，若O 沿 BP 方向移动，当O 与 PA 相切时，圆心 O 移动的距离为 cm.12.读一读：式子“1+2+3+4+100”表示从 1 开始的 100 个连续自然数的和，由于式子比第 13 题图第 11 题图第 7 题图3较长，书写不方便，为了简便起见，我们将其表示为 ，这里10n“”是求和符号.通过对以上材料的阅读 ，计算 =_.2014n)(13. 如图，直线 AB 交双曲线 于 A、B，交 x 轴于点 C,B 为线段 AC 的中点，过点kyxB 作 BMx 轴于 M，连结 OA.若 OM=2MC, =12.则 k 的值为_.OCS14.如图，在平面
5、直角坐标系中，直线 l：y =x+2 交 x 轴于点 A，交 y 轴于点 A1，点A2，A 3，在直线 l 上，点 B1，B 2，B 3，在 x 轴的正半轴上，若A 1OB1，A 2B1B2，A3B2B3，依次均为等腰直角三角形，直角顶点都在 x 轴上，则第 n 个等腰直角三角形AnBn1 Bn顶点 Bn的横坐标为 三、解答题(本题共 78 分，把解答和证明过程写在答题卡的相应区域内)15.(本小题 6 分)计算： .01|3|2cos30（ ） （ ） 16.(本小题 6 分) 先化简，再求值： ，其中 29864xx7417.(本小题 6 分)如图，在四边形 ABCD 中，E 是 AB 的
6、中点，ADEC，AED=B（1）求证：AEDEBC （2）当 AB=6 时，求 CD 的长 18.(6 分)某超市预测某饮料有发展前途，用 1600 元购进一批饮料，面市后果然供不应求，又用 6000 元购进这批饮料，第二批饮料的数量是第一批的 3 倍，但单价比第一批贵 2 元14 题图第 17 题图4（1）第一批饮料进货单价多少元？（2）若二次购进饮料按同一价格销售，两批全部售完后，获利不少于 1200 元，那么销售单价至少为多少元？19.(本小题 7 分)如图，一次函数 y1=-x+2 的图象与反比例函数 的图象相交于 A，B2kyx两点，与 x 轴相交于点 C已知 tanBOC= ，2点
7、 B 的坐标为（m，n）（1）求反比例函数的解析式；（2）请直接写出当 xm 时，y 2的取值范围20.(本小题 7 分)如图，甲、乙两只捕捞船同时从 A 港出海捕鱼，甲船以 15 千米/小时2的速度沿北偏西 60方向前进，乙船以 15 千米/小时的速度沿东北方向前进，甲船航行 2小时到达 C 处，此时甲船发现渔具丢在乙船上，于是甲船加快速度(匀速)沿北偏东 75的方向追赶乙船，结果两船在 B 处相遇(1)甲船从 C 处追赶上乙船用了多少时间？(2)求甲船追赶乙船时的速度(结果保留根号) 21. (本小题 10 分)如图，AB 是O 的直径，C 是O 上的一点，过点 A 作 ADCD 于点 D
8、，交O 于点 E，且 AB（1）求证：CD 是O 的切线；（2）若 tanCAB= ，BC=3，求 DE 的长 3422(本小题 10 分)某学校为了增强学生体质，决定开设以下体育课外活动项目：A篮球 B乒乓球 C羽毛球 D足球，为了解学生最喜欢哪一种活动项目，随机抽取了部分学生进行调查，并将调查结果绘制成了两幅不完整的统计图，请回答下列问题：20 题图EDOCB A第 19 题图5（1）这次被调查的学生共有多少人；（2）请你将条形统计图（2）补充完整；（3）在平时的乒乓球项目训练中，甲、乙、丙、丁四人表现优秀，现决定从这四名同学中任选两名参加乒乓球比赛，求恰好选中甲、乙两位同学的概率（用树状
9、图或列表法解答）23.(本小题 10 分)如图 1，将菱形纸片 AB（E）CD（F）沿对角线 BD（EF）剪开，得到ABD和ECF，固定ABD，并把ABD 与ECF 叠放在一起（1）操作：如图 2，将ECF 的顶点 F 固定在ABD 的 BD 边上的中点处，ECF 绕点 F 在BD 边上方左右旋转，设旋转时 FC 交 BA 于点 H（H 点不与 B 点重合），FE 交 DA 于点 G（G点不与 D 点重合）求证：BHGD=BF 2（2）操作：如图 3，ECF 的顶点 F 在ABD 的 BD 边上滑动（F 点不与 B、D 点重合），且CF 始终经过点 A，过点 A 作 AGCE，交 FE 于点
10、G，连接 DG探究：FD+DG= 请予证明24.(本小题 10 分)已知二次函数 的图象如图.2134yx（1）求它的对称轴与 x 轴交点 D 的坐标；（2）将该抛物线沿它的对称轴向上平移，设平移后的抛物线与 x 轴，y 轴的交点分别为A、B、C 三点，若ACB=90，求此时抛物线的解析式；（3）设（2）中平移后的抛物线的顶点为 M，以 AB 为直径，D 为圆心作D，试判断直线 CM与D 的位置关系，并说明理由.第 23 题图第 24 题图6郓城县二 O 一九初中数学中考县级统考模拟试题试题参考答案及评分标准一、选择题(本大题共 8 个小题，每小题 3 分，共 24 分)1C 2.D 3.A
11、4.A 5.D 6.C 7.B 8.D 二、填空题(本大题共 6 个小题，每小题 3 分 ，共 18 分，只要求填写最后结果，每小题填对得 3 分)9.12 10.三 11.1 或 5 12. 13.8 14.2n+12 2014三、解答题(本题共 78 分)15.解： 01|3|cos3（ ） -（ ） 4 分312. 6 分=-316. 解：原式= =298164xx23)(43xx（= = ，4 分4当 时7x原式= = 6 分3-417（1）证明：ADEC，7A=BEC， E 是 AB 中点，AE=EB， AED=B，AEDEBC3 分（2）AEDEBCAD=EC又AD/EC四边形 A
12、ECD 是平行四边形AE=CDAE=EBCD=36 分18. 解：（1）设第一批饮料进货单价为 x 元，则第二批饮料进货单价为（x+2）元，根据题意得：3 = ，解得：x=8，经检验，x=8 是分式方程的解答：第一批饮料进货单价为 8 元3 分（2）设销售单价为 m 元，根据题意得：200（m8）+600（m10）1200，解得：m11答：销售单价至少为 11 元6 分 19.解：（1）如图，过点 B 作 BDX 轴于点 D,在 Rt OBD 中， 1tanBOC22Dnmn即8把点 B（m，n）代入 y1=x+2 得 n=m+2，n=2n+2，解得 n=2. m=4. B 点坐标为（4， 2
13、）.把 B（4，2）代入 得 k=4（2）=8，kyx反比例函数解析式为 .5 分2-（2）当 x4，y 2 的取值范围为 y20 或 y227 分20. 解：(1)如解图，过点 A 作 ADBC 于 D，由题意得：B=30，BAC=6045=105，则BCA=45，AC=30 千米，2在 RtADC 中，AD=CD=ACcos45=30(千米)，在 RtBAD 中，AB=2AD=60 千米，t= =4(时). 601542=2(时)，答：甲船从 C 处追赶上乙船用了 2 小时；4 分(2)由(1)知：BD=ABcos30=30 千米，3BC=3030 (千米)，3甲船追赶乙船的速度 v=(3
14、030 )2=(1515 )千米/时. 3答：甲船追赶乙船时的速度为：(1515 )千米/小时7分21.（1）证明：连接 OC， ，ABCEOAC=CAD，OA=OC，EDOCB A9OAC=OCA，CAD=OCA，OCAD，ADCD，OCCD，CD 是O 的切线4 分（2）解：AB 是O 的直径，ACB=90，在 RtACB 中，AC= =4，3tan4BCAAB= =5，2ADCD，ADC=ACB=90，又BAC=CAD，ACBADC， ，BCDA ，CD=2.4，354四边形 ABCE 内接于O，ABC+AEC=180又DEC+AEC=180CED=ABC，又ADC=ACB=90，CDE
15、ACB， ，DEBCA ，32.4DE=1.810 分解法二：由已知可求得 BC=3，AC=4，由于 tanCAB= ， tanCAD=3434可设 CD=3a，AD=4a,由勾股定理得 CD= ，125由于 ，得到 BC=CE=3，ABCE10由勾股定理得 DE22.解：（1）根据题意得：20 =200（人），则这次被调查的学生共有 200 人；3 分 （2）补全图形，如图所示：6 分 （3）列表如下：所有等可能的结果为 12 种，其中符合要求的只有 2 种，8 分则 P= = 10 分1623.证明：（1）将菱形纸片 AB（E）CD（F）沿对角线 BD（EF）剪开，B=D，将ECF 的顶点
16、 F 固定在ABD 的 BD 边上的中点处，ECF 绕点 F 在 BD 边上方左右旋转，BF=DF，HFG=B，又HFD=HFG+GFD=B+BHFGFD=BHF，BFHDGF，甲 乙 丙 丁甲 （乙，甲） （丙，甲） （丁，甲）乙 （甲，乙） （丙，乙） （丁，乙）丙 （甲，丙） （乙，丙） （丁，丙）丁 （甲，丁） （乙，丁） （丙，丁） 11 ，BHGD=BF 2；5 分（2）AGCE，FAG=C，CFE=CEF，AGF=CFE，AF=AG，BAD=C，BAF=DAG，又AB=AD，ABFADG，FB=DG，FD+DG=BD，10 分24.解: （1）由 得 2134yx32bxa（3，
17、0）2 分（2）方法一:如图 1, 设平移后的抛物线的解析式为2134yxk则 C OC=(0,)令 即 y20xk得 1349xk2349A ，B(,0)(,)k122 2(49349)163ABkk 2 2(49)Ck836k 2即: 8361kk得 (舍去)1420抛物线的解析式为 6 分234yx方法二: 2134yx顶点坐标 9,设抛物线向上平移 h 个单位则得到 ,顶点坐标 0C93,4Mh平移后的抛物线: 21yx当 时, 0y29304h13xh24x A B (9,)(9,)ACB=90 AOCCOB OAOB2OC493493hh13解得 ,14h20舍 去平移后的抛物线:
18、 22191534344yxx（3）方法一:如图 2, 由抛物线的解析式 可得2A(-2 ，0)，B(8，0) ，C(，0) ，M 5(3,)4过 C、M 作直线，连结 CD，过 M 作 MH 垂直 y 轴于 H则 3H 2256()41D2253(4)16在 RtCOD 中,CD= =AD 点 C 在D 上 2256()41DM256()41 22CCDM 是直角三角形，CDCM直线 CM 与D 相切10 分 方法二:如图 3, 由抛物线的解析式可得A(-2 ，0)，B(8，0) ，C(，0) ，M 25(3,)4作直线 CM,过 D 作 DECM 于 E, 过 M 作 MH 垂直 y 轴于 H则 , 3H25414由勾股定理得 154CMDMOC MCH=EMDRtCMHRtDME 得 DEMHC5DE由(2)知 10ABD 的半径为 5 直线 CM 与D 相切
