1、4一年之中地球与太阳之间的距离随时间而变化，1 个天文单位是地球与太阳之间的平均距离，即 1.4960 亿千米用科学记数法表示 1 个天文单位应是（ ）A1.496010 7 千米 B14.96010 7 千米C1.496010 8 千米 D0.14960 108 千米5已知反比例函数 y 的图象经过点（2，2） ，则 k 的值为（ ）A4 B C4 D26在“大家跳起来”的乡村学校舞蹈比赛中，某校 10 名学生参赛成绩统计如图所示对于这 10 名学生的参赛成绩，下列说法中错误的是（ ）A众数是 90 B中位数是 90 C平均数是 90 D极差是 157用半
2、径为 3cm，圆心角是 120的扇形围成一个圆锥的侧面，则这个圆锥的底面半径为（ ）A2cm B1.5cm Ccm D1cm8如图，在ABC 中，C90，B30，以 A 为圆心，任意长为半径画弧分别交AB、 AC 于点 M 和 N，再分别以 M、N 为圆心，大于 MN 的长为半径画弧，两弧交于点 P，连结 AP 并延长交 BC 于点 D，则下列说法中正确的个数是（ ）AD 是BAC 的平分线； ADC60；点 D 在 AB 的中垂线上；S DAC：S ABC 1：3A1 B2 C3 D4二、填空题（每小题 3 分，共 30 分）9分解因式：x 264 &n
3、bsp; 10一个多边形的内角和等于 1260，则这个多边形是 边形11已知 是二元一次方程组 的解，则 m+3n 的立方根为 12若等腰三角形的一个角为 50，则它的顶角为 13为庆祝“六一”儿童节，某幼儿园举行用火柴棒摆“金鱼”比赛如图所示：按照上面的规律，摆第（n）图，需用火柴棒的根数为 14如图，在 RtABC 中，ACB90，D 是 AB 的中点，过 D 点作 AB 的垂线交 AC于点 E， BC6，sinA ，则 DE 15若关于 x 的函数
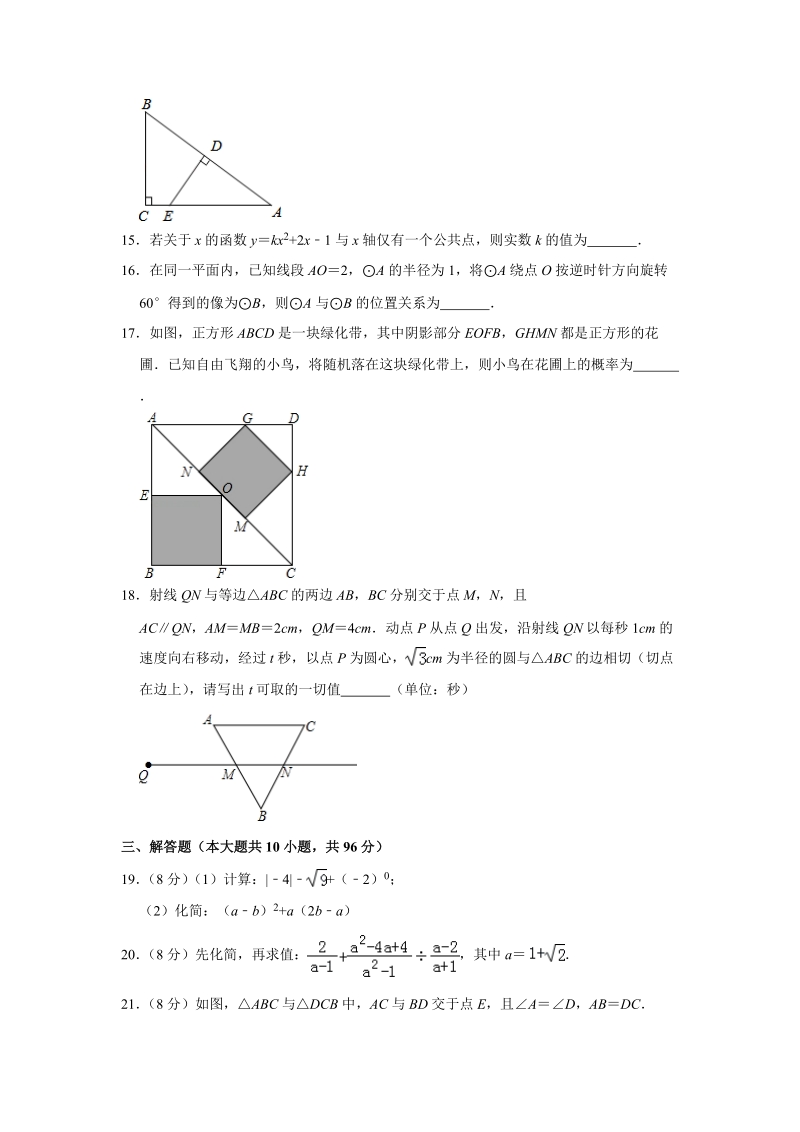
4、ykx 2+2x1 与 x 轴仅有一个公共点，则实数 k 的值为 16在同一平面内，已知线段 AO2，A 的半径为 1，将A 绕点 O 按逆时针方向旋转60得到的像为B，则 A 与B 的位置关系为 17如图，正方形 ABCD 是一块绿化带，其中阴影部分 EOFB，GHMN 都是正方形的花圃已知自由飞翔的小鸟，将随机落在这块绿化带上，则小鸟在花圃上的概率为 18射线 QN 与等边ABC 的两边 AB，BC 分别交于点 M，N，且ACQN，AMMB 2cm， QM4cm动点 P 从点 Q 出发，沿射线
5、QN 以每秒 1cm 的速度向右移动，经过 t 秒，以点 P 为圆心， cm 为半径的圆与ABC 的边相切（切点在边上） ，请写出 t 可取的一切值 （单位：秒）三、解答题（本大题共 10 小题，共 96 分）19 （8 分） （1）计算：|4| +（2） 0； （2）化简：（ab） 2+a（2ba）20 （8 分）先化简，再求值： ，其中 a 21 （8 分）如图，ABC 与DCB 中，AC 与 BD 交于点 E，且AD，ABDC（1）求证：ABEDCE；（2）当AEB50，求EBC 的度数？22 （8 分）了解学生零花钱的使用情况，校团委随机调查了本
6、校部分学生每人一周的零花钱数额，并绘制了如图甲、乙所示的两个统计图（部分未完成） 请根据图中信息，回答下列问题：（1）校团委随机调查了多少学生？请你补全条形统计图；（2）表示“50 元”的扇形的圆心角是多少度？被调查的学生每人一周零花钱数的中位数是多少元？（3）全校 1000 名学生每人自发地捐出一周零花钱的一半，以支援灾区建设请估算全校学生共捐款多少元？23 （10 分）高考英语听力测试期间，需要杜绝考点周围的噪音如图，点 A 是某市一高考考点，在位于 A 考点南偏西 15方向距离 125 米的 C 处有一消防队在听力考试期间，消防队突然接到报警电话，告知在位于 C 点北偏东 75方向的 F
7、 点处突发火灾，消防队必须立即赶往救火已知消防车的警报声传播半径为 100 米，若消防车的警报声对听力测试造成影响，则消防车必须改进行驶，试问：消防车是否需要改道行驶？请说明理由 （ 取 1.732）24 （10 分）如图，一次函数 ykx+1（k0）与反比例函数 y （m0）的图象有公共点 A（1 ，2） 直线 lx 轴于点 N（3，0） ，与一次函数和反比例函数的图象分别交于点B，C （1）求一次函数与反比例函数的解析式；（2）求ABC 的面积？25 （10 分）经过某十字路口的汽车，它可能继续直行，也可能向左转或向右转，如果这三种情况是等可能的，当三辆汽车经过这个十字路口时：（1）求三辆
8、车全部同向而行的概率；（2）求至少有两辆车向左转的概率；（3）由于十字路口右拐弯处是通往新建经济开发区的，因此交管部门在汽车行驶高峰时段对车流量作了统计，发现汽车在此十字路口向右转的频率为 ，向左转和直行的频率均为 目前在此路口，汽车左转、右转、直行的绿灯亮的时间分别为 30 秒，在绿灯亮总时间不变的条件下，为了缓解交通拥挤，请你用统计的知识对此路口三个方向的绿灯亮的时间做出合理的调整26 （10 分）背景资料一棉花种植区的农民研制出采摘棉花的单人便携式采棉机，采摘效率高，能耗低，绿色环保，经测试，一个人操作该采棉机的采摘效率为 35 公斤/时，大约是一个人手工采摘的 3.5 倍，购买一台采棉
9、机需 900 元，雇人采摘棉花，按每采摘 1 公斤棉花 a 元的标准支付雇工工钱，雇工每天工作 8 小时问题解决（1）一个雇工手工采摘棉花，一天能采摘多少公斤？（2）一个雇工手工采摘棉花 7.5 天获得的全部工钱正好购买一台采棉机，求 a 的值；（3）在（2）的前提下，种植棉花的专业户张家和王家均雇人采摘棉花，王家雇佣的人数是张家的 2 倍，张家雇人手工采摘，王家所雇的人中有 的人自带采棉机采摘， 的人手工采摘，两家采摘完毕，采摘的天数刚好一样，张家付给雇工工钱总额为 14400 元，王家这次采摘棉花的总重量是多少？27 （12 分）如图 1，正方形 ABCD 的边长为 2，点 M 是 BC
10、的中点，P 是线段 MC 上的一个动点（不与 M、C 重合） ，以 AB 为直径作 O，过点 P 作O 的切线，交 AD 于点F，切点为 E（1）求证：OFBE ；（2）设 BPx，AFy，求 y 关于 x 的函数解析式，并写出自变量 x 的取值范围；（3）延长 DC、FP 交于点 G，连接 OE 并延长交直线 DC 于 H（图 2） ，问是否存在点P，使EFO EHG（E、F、O 与 E、H、G 为对应点）？如果存在，试求（ 2）中 x和 y 的值；如果不存在，请说明理由28 （12 分）如图 1，平面直角坐标系中，等腰直角三角形的直角边 BC 在 x 轴正半轴上滑动，点 C 的坐标为（t，
11、0 ） ，直角边 AC4，经过 O，C 两点做抛物线 y1ax（xt）（a 为常数，a0） ，该抛物线与斜边 AB 交于点 E，直线 OA：y 2kx（k 为常数，k0）（1）填空：用含 t 的代数式表示点 A 的坐标及 k 的值：A ，k ；（2）随着三角板的滑动，当 a 时：请你验证：抛物线 y1ax（xt ）的顶点在函数 y 的图象上；当三角板滑至点 E 为 AB 的中点时，求 t 的值；（3）直线 OA 与抛物线的另一个交点为点 D，当 txt+4，|y 2y 1|的值随 x 的增大而减小，当 xt+4 时，|y 2y
12、 1|的值随 x 的增大而增大，求 a 与 t 的关系式及 t 的取值范围参考答案一、选择题（每小题 3 分，共 24 分）1 【解答】解：6 的倒数是 故选：D2 【解答】解：A、|2|2，故 A 选项正确；B、 （a 2） 3a 6，故 B 选项错误；C、2x 2+3x25 x2，故 C 选项正确；D、 2 ，故 D 选项正确故选：B3 【解答】解：所给图形的俯视图是 A 选项所给的图形故选：A4 【解答】解：将 1.4960 亿千米用科学记数法表示为：1.496010 8 千米故选：C5 【解答】解：反比例函数 y 的图象经过点（2，2） ，kxy2（2）4故选：C6 【解答】解：90
13、出现了 5 次，出现的次数最多，众数是 90；故 A 正确；共有 10 个数，中位数是第 5、6 个数的平均数，中位数是（90+90）290；故 B 正确；平均数是（801+852+905+95 2）1089；故 C 错误；极差是：958015；故 D 正确综上所述，C 选项符合题意，故选：C7 【解答】解：设此圆锥的底面半径为 r，根据圆锥的侧面展开图扇形的弧长等于圆锥底面周长可得，2r ，解得：r1cm故选：D8 【解答】解：根据作图的过程可知，AD 是BAC 的平分线故正确；如图， 在 ABC 中，C 90，B30，CAB60又AD 是BAC 的平分线，12 CAB30，390260，即
14、ADC60故正确； 1B 30，ADBD ，点 D 在 AB 的中垂线上故正确；如图，在直角ACD 中，230，CD AD，BCCD+BD AD+AD AD，S DAC ACCD ACADS ABC ACBC AC AD ACAD，S DAC ：S ABC ACAD： ACAD1：3故正确综上所述，正确的结论是：，共有 4 个故选：D二、填空题（每小题 3 分，共 30 分）9 【解答】解：x 264（x+8） （x 8） 故答案为：（x+8） （x 8） 10 【解答】解：根据题意，得（n2）1801260，解得 n911 【解答】解：把 代入方程组 ，得： ，则两式相加得：m+3n8，所以
15、 2故答案为 212 【解答】解：当该角为顶角时，顶角为 50；当该角为底角时，顶角为 80故其顶角为 50或 80故填 50或 8013 【解答】方法一：解：第 1 个图形有 8 根火柴棒，第 2 个图形有 14 根火柴棒，第 3 个图形有 20 根火柴棒，第 n 个图形有 6n+2 根火柴棒故答案为：6n+2方法二：当 n1 时，s8，当 n2 时，s14，当 n3 时，s20，经观察，此数列为一阶等差，设 skn+b， ，s6n+214 【解答】解：BC6， sinA ，AB10，AC 8，D 是 AB 的中点，AD AB5，ADEACB， ，即 ，解得：DE 故答案为： 15 【解答】
16、解：令 y0，则 kx2+2x10关于 x 的函数 ykx 2+2x 1 与 x 轴仅有一个公共点，关于 x 的方程 kx2+2x10 只有一个根当 k0 时，2x10，即 x ，原方程只有一个根，k0 符合题意；当 k0 时，4+4 k0，解得，k1综上所述，k0 或1故答案为：0 或116 【解答】解：A 绕点 O 按逆时针方向旋转 60得到的 B，OAB 为等边三角形，ABOA 2， A、B 的半径都为 1，AB 等于两圆半径之和， A 与B 外切故答案为外切17 【解答】解：设正方形的 ABCD 的边长为 a，则 BF BC ，ANNMMC a，阴影部分的面积为（ ） 2+（ a） 2
17、 a2，小鸟在花圃上的概率为 ，故答案为： 18 【解答】解：ABC 是等边三角形，ABACBCAM +MB 4cm，AC B60，QNAC，AM BMN 为 BC 中点，MN AC2cm，BMNBNMC A60，分为三种情况：如图 1，当 P 切 AB 于 M时，连接 PM，则 PM cm，PMM90，PMM BMN60，MM1cm，PM2MM2cm，QP4cm2 cm2cm，即 t2；如图 2，当 P 于 AC 切于 A 点时，连接 PA，则CAPAPM90，PMABMN60，AP cm，PM1cm，QP4cm1 cm3cm，即 t3，当 P 于 AC 切于 C 点时，连接 PC ，则CP
18、NACP90，P NCBNM60，CP cm，PN1cm，QP4cm+2 cm+1cm7cm，即当 3t7 时，P 和 AC 边相切；如图 3，当 P 切 BC 于 N时，连接 PN则 PN cm，PNN90，PNN BNM60，NN1cm，PN2NN 2cm，QP4cm+2 cm+2cm8cm，即 t8；注意：由于对称性可知，当 P 点运动到 AB 右侧时也存在P 切 AB，此时 PM 也是为2，即 P 点为 N 点，同理可得 P 点在 M 点时， P 切 BC这两点都在第二种情况运动时间内故答案为：t2 或 3t7 或 t8三、解答题（本大题共 10 小题，共 96 分）19 【解答】解：
19、（1）原式43+12；（2）原式a 22ab+b 2+2aba 2b 220 【解答】解：原式 + + ，当 a1+ 时，原式 21 【解答】 （1）证明：在ABE 和DCE 中ABE DCE（AAS） ；（2）解：ABEDCE，BEEC，EBCECB，EBC+ ECBAEB50，EBC2522 【解答】解：（1）随机调查的学生数是：1025%40（人） ，零花钱是 20 元的人数是：4015%6（人） （2）50 元的所占的比例是： ，则圆心角 36，中位数是 30 元；（3）学生的零用钱是： 33（元） ，则全校学生共捐款 33100016500 元23 【解答】解：如图：过点 A 作 A
20、HCF 于点 H，由题意得：MCF75，CAN15，AC 125 米，CMAN，ACMCAN15，ACHMCFACM751560，在 RtACH 中，AHAC sinACH125 108.25（米）100 米答：消防车不需要改道行驶24 【解答】解：（1）将 A（1，2）代入一次函数解析式得：k+12，即 k1，一次函数解析式为 yx +1；将 A（1，2）代入反比例解析式得：m 2，反比例解析式为 y ；（2）N（3，0） ，点 B 横坐标为 3，将 x3 代入一次函数得：y 4，将 x3 代入反比例解析式得： y ，即 CN ，BC 4 ，A 到 BC 的距离为：2，则 SABC 2 25
21、 【解答】解：（1）分别用 A，B，C 表示向左转、直行，向右转；根据题意，画出树形图：共有 27 种等可能的结果，三辆车全部同向而行的有 3 种情况，P（三车全部同向而行） ；（2）至少有两辆车向左转的有 7 种情况，P（至少两辆车向左转） ；（3）汽车向右转、向左转、直行的概率分别为 ，在不改变各方向绿灯亮的总时间的条件下，可调整绿灯亮的时间如下：左转绿灯亮时间为 90 27（秒） ，直行绿灯亮时间为 90 27（秒） ，右转绿灯亮的时间为 90 36（秒） 26 【解答】解：（1）一个人操作该采棉机的采摘效率为 35 公斤/时，大约是一个人手工采摘的 3.5 倍，一个人手工采摘棉花的效率
22、为：353.510（公斤/时） ，雇工每天工作 8 小时，一个雇工手工采摘棉花，一天能采摘棉花：10880（公斤） ；（2）由题意，得 807.5a900，解得 a ；雇工工钱的标准为：每采摘 1 公斤棉花 元；（3）设张家雇佣 x 人采摘棉花，则王家雇佣 2x 人采摘棉花，其中王家所雇的人中有的人自带采棉机采摘， 的人手工采摘张家雇佣的 x 人全部手工采摘棉花，且采摘完毕后，张家付给雇工工钱总额为 14400元，采摘的天数为： ，即： ，王家这次采摘棉花的总重量是：（358 +80 ） 51200（公斤） 27 【解答】 （1）证明：连接 OEFE、FA 是O 的两条切线FAOFEO90在
23、Rt OAF 和 RtOEF 中，RtFAORtFEO（HL） ，AOFEOF AOE，AOFABE，OFBE，（2）解：过 F 作 FQBC 于 QPQBPBQx yPFEF+EPFA+BPx+ y在 RtPFQ 中FQ 2+QP2PF 22 2+（xy） 2（x +y） 2化简得： ， （1x2） ；（3）存在这样的 P 点，理由：EOFAOF ，EHG EOA2EOF，当EFOEHG2EOF 时，即EOF30时，RtEFORtEHG，此时 RtAFO 中，yAF OAtan30 ，当 时，EFOEHG28 【解答】解：（1）点 C 的坐标为（t ，0） ，直角边 AC4，点 A 的坐标是
24、（t，4） 又直线 OA：y 2kx（k 为常数，k0） ，4kt，则 k （k 0） （2） 当 a 时，y 1 x（xt ） ，其顶点坐标为（ ， ） 对于 y 来说，当 x 时，y ，即点（ ， ）在抛物线y 上故当 a 时，抛物线 y1ax（x t）的顶点在函数 y 的图象上；如图 1，过点 E 作 EKx 轴于点 KACx 轴，ACEK点 E 是线段 AB 的中点，K 为 BC 的中点，EK 是ACB 的中位线，EK AC2，CK BC2，E（t+2，2） 点 E 在抛物线 y1 x（xt）上， （t+2） （t+2t）2，解得 t2（3）如图 2， ，则 xax（x t） ，解得
25、x +t，或 x0（不合题意，舍去） 故点 D 的横坐标是 +t当 x +t 时，|y 2y 1|0，由题意得 t+4 +t，at1y 2y 1 x ax（xt） ax 2+（at+ ）xax 2 （t + ）x+（ + ） 2+a（+ ） 2ax （ + ） 2+a（ + ） 2当 x + 时，y 2y 1 取得最大值，又当 x +t 时，|y 2y 1|0，当 + x +t 时，|y 2y 1|随 x 的增大而减小；当 x +t 时，|y 2y 1|随 x 的增大而增大根据题意需要满足当 tx t+4，|y 2y 1|的值随 x 的增大而减小，当 xt+4 时，|y 2y 1|的值随 x 的增大而增大，t + 可满足条件，at1，解得 t4综上所述，a 与 t 的关系式及 t 的取值范围为 at1（t 4）
