1、20182019 学年第一学期期末教学质量调研测试初三数学 2019.01(本试卷由选择题、填空题和解答题三大题组成.共 28 小题，满分 130 分.考试时间 120 分钟.)注意事项:1.答题前，考生务必将自己的学校、班级、姓名、考试号等信息用 0.5 毫米黑色墨水签字笔填写在答题纸的相应位置上;2.答选择题必须用 2B 铅笔把答题纸上对应题目的答案标号涂黑，如需改动，请用橡皮擦干净后，再选涂其他答案;答非选择题必须用 0.5 毫米黑色墨水签字笔写在答题纸指定的位置上，不在答题区域内的答案一律无效，不得用其他笔答题;3.保持卷面清洁，不要折叠，不要弄破。答在试卷和草稿纸上一律无效.一、选择
2、题(本大题共有 10 小题，每小题 3 分，共 30 分.在每小题所给出的四个选项中，只有一项是符合题目要求的.)1.方程 x2=1 的解是A. B. C. D. 11x1x12x2.两个相似多边形的相似比是 2：3，则这两个多边形的周长比是A. B. C. D. 4:9:2:5:33.如图，在 中， ， ， ，则 的值是ABC90AC1BsinAA. B. 12 2C. D. 5 54.一组数据 ，则这组数据的方差为1,20,A. 0 B. 1 C. 2 D .105.已 知 关 于 的 一 元 二 次 方 程 有 两 个 不 相 等 的 实 数 根 ， 则 实 数 的 取 值 范 围x23
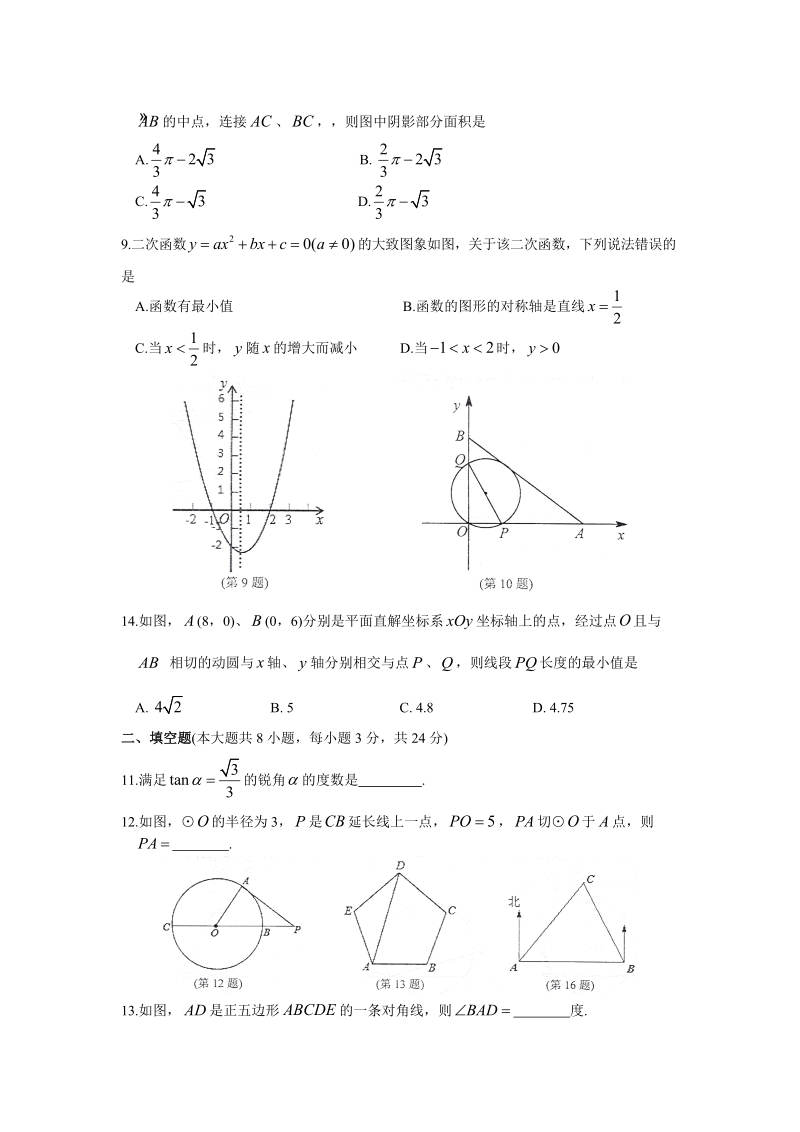
3、0xmm为A. B. C. D. 94m9494946.二次函数 的图象的对称轴是23yxA.直线 B.直线 C.直线 D.直线11xxx7.要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划 7 天，每天安排 4 场比赛.设比赛组织者应邀请 个队参赛，则 满足的关系式为A. B. C. D. 1()28x1()28x(1)28x(1)28x8.如图，扇形 中，半径 ， ， 是AOBA0OBC的中点，连接 、 ，则图中阴影部分面积是CA. B. 42323C. D.9.二 次 函 数 的 大 致 图 象 如 图 ， 关 于 该 二 次 函 数 ， 下 列 说 法
4、 错 误 的20()yaxbca是A.函数有最小值 B.函数的图形的对称轴是直线 12xC.当 时， 随 的增大而减小 D.当 时，12xyx12x0y14.如图， (8，0)、 (0，6) 分别是平面直解坐标系 坐标轴上的点，经过点 且与ABxOyO相切的动圆与 轴、 轴分别相交与点 、 ，则线段 长度的最小值是xyPQPA. B. 5 C. 4.8 D. 4.7542二、填空题(本大题共 8 小题，每小题 3 分，共 24 分)11.满足 的锐角 的度数是 .3tan12.如图， 的半径为 3， 是 延长线上一点， ， 切 于 点，则OPCB5POAPA.13.如图， 是正五边形 的一条对
5、角线，则 度.ADBCEBAD14.下列说法:必然事件的概率为 1；数据 1、2、2、3 的平均数是 2；数据 5, 2、3、0 的极差是 8；如果某种游戏活动的中奖率为 40%，那么参加这种活动 10 次必有4 次中奖.其中正确的有 个.15.一个圆锥的侧面展开图是半径为 6 的半圆，则这个圆锥的底面半径为 . 16.如图，在一笔直的海岸线上有 、 两个观测站， 在 的正西方向， km，ABABAB从 测得船 在北偏东 45 的方向，从 测得船 在北偏西 30 的方向，则船 离海ACCC岸线的距离是 .17.如图， 内接于 ， 是 的直径，BO. 30平分 交 于 ，交 于点 ，连接 ,EE
6、ABDAE若的面积是 5，则 的面积是 .ADC18.某数学兴趣小组研究二次函数 的图像时发2yxm现:无论 如何变化，该图像总经过一个定点，这个定点的m坐标是 .三、解答题(本大题共 10 小题，共 76 分，把解答过程写在答题纸相应的位置上，解答时应写出必要的计算过程、推演步骤或文字说明.)19.(本题满分 4 分)计算: 08(12sin4520.(本题满分 8 分，每小题 4 分)解方程:(1) ; (2) .213x229(1)0x21.(本题满分 6 分)如图， 是 的边 上的点， ，过 作 交 于 . DABC3DBA/DEBCAE、 相交于 .EF(1)若 ，则 ;2(2)求:
7、 的值，22.(本题满分 6 分)为了解本学期初三期中调研测试数学试题的命题质量与难度系数，命题教师选取了一个水平相当的初三年级进行分析研究，随机抽取部分学生成绩(得分为整数，满分为 130 分) 分为 5 组:第一组 5570，第二组 7085，第三组 85100，第四组 100115，第五组115130;统计后得到如图所示的频数分布直方图 (每组含最小值不含最大值)和扇形统计图，观察图形的信息，回答下列问题:(1)本次调查共随机抽取了该年级多少名学生?并将频数分布直方图补充完整;(2)若将得分转化为等级，规定:得分低于 70 分评为“D ”，70100 分评为“C”，100115 分评为“
8、B”，115 130 分评为“A”，那么该年级 1500 名考生中，考试成绩评为“B”的学生大约有多少名 ?23.(本题满分 7 分)颖颖和丽丽做“摸球”游戏:在一个不透明的袋子中装有编号为 14 的四个球(除编号外都相同)，从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字.若两次数字之和大于 5，则颖颖胜，否则丽丽胜.这个游戏对双方公平吗?请说明理由.24.(本题满分 7 分)某地区 2015 年投入教育经费 2900 万元，2017 年投入教育经费 3509 万元.(1)求 2015 年至 2017 年该地区投入教育经费的年平均增长率 ;(2)按照义务教育法规定，教育经费的投
9、入不低于国民生产总值的百分之四，结合该地区国民生产总值的增长情况，该地区到 2019 年需投入教育经费 4250 万元，如果按(1)中教育经费投入的增长率，到 2019 年该地区投入的教育经费是否能达到 4250 万元?请说明理由.(参考数据: ， ， ， )1.21.4.21.69.31.6.425.(本题满分 8 分)如图， 是 的直径， 是弦， ， 于 .ABOAC12DAOCD(1)求证: 是 的切线:CD(2)若 ，求 的值.10,2cos26.(本题满分 I0 分)问题 1 如图点 、 、 在 上，且 ， 的半径是 3.求 的ABCO120ABCOAC长.问题 2 如图点 、 、
10、、 在 上，且 ， 是 的延长线上的ABCDOABCEA.1,3BEFE(1)设 ，则 ;Dng(2)如图若 是线段 上的一个点，且 .试探究，在 上是否存在点 (GB12GBDOP除外)使 ?为什么? BPF27.(本题满分 10 分)如图，在矩形 中，动点 从 出发，以相同的速度，沿ABCDPA方向运动到点 处停止.设点 运动的路程为 , 面积PxPAB为 ， 与 的函数图象如图所示.yx(1)矩形 的面积为 ;(2)如图，若点 沿 边向点 以每秒 1 个单位的速度移动，同时，点 从点 出Q发沿 边向点 以每秒 2 个单位的速度移动.如果 、 两点在分别到达 、B两点后就停止移动，回答下列
11、问题:C当运动开始 秒时，试判断 的形状;3DPQ在运动过程中，是否存在这样的时刻，使以 为圆心， 的长为半径的圆与矩形PQ的对角线 相切，若存在，求出运动时间;若不存在，请说明理由.ABCDA28.(本题满分 10 分)已知二次函数 的图象与 轴分别交于点 、 ( 在2yxbcxAB左侧)，与 轴交于点 ，若将它的图象向上平移 4 个单位长度，再向左平移 5 个单位yC长度，所得的抛物线的顶点坐标为 .(,0)(1)原抛物线的函数解析式是 .(2)如图，点 是线段 下方的抛物线上的点，求 面积的最大值及此时点PBPBC的坐标;(3)如图，点 是线段 上一动点，连接 ，在线段 上是否存在这样的
12、点 ，QOM使 为等腰三角形且 为直角三角形?若存在，求点 的坐标;若不存在，CMM请说明理由.参考答案1、选择题1、B 2、D 3、C 4、C 5、A 6、B 7、A 8、A 9、D 10、C2、填空11、 ；12、4；13、72；14、3；15、3；16、 ；17、 ；18、(1,1)0 32153、解答题19、 ；1220、（1） ；（2）31,321xx 41,21x21、（1） （2）6EC4FD22、（1）50 人；第五组 4 人图略23、不公平；原因：小颖赢的概率 ，小丽赢的概率 ， ，故而不公平。8385324、（1）设平均增长率为 ，x)(1.2,.059)(291舍x（2）
13、 42508.%(35故而不能达到25、（1）过程略。（思路：证明 即可得）ABCD（3） 5cosOAC26、问题 1： 2问题 2：（1） 3n（2）过点 B 作 AE 的垂线，与圆的交点即是点 P。证明过程略，思路：由（1）可证 BG=BF，即得。27、（1）72；（2） 为直角三角形（勾股定理可证）DPQ（3）不存在。理由：假设存在，连接 AC，过点 Q 作 QM 垂直于 AC 垂足为点 M。则 QM=PQ，即得： 2M即 xx4)6()21(52化简得： 017此 方 程 无 解 ， 即 不 存 在028、（1） 562xy（2）最大值 ），的 坐 标 （点 415-2P,81（3）点 M 的坐标： 或）（ 50-1,-)2,(
