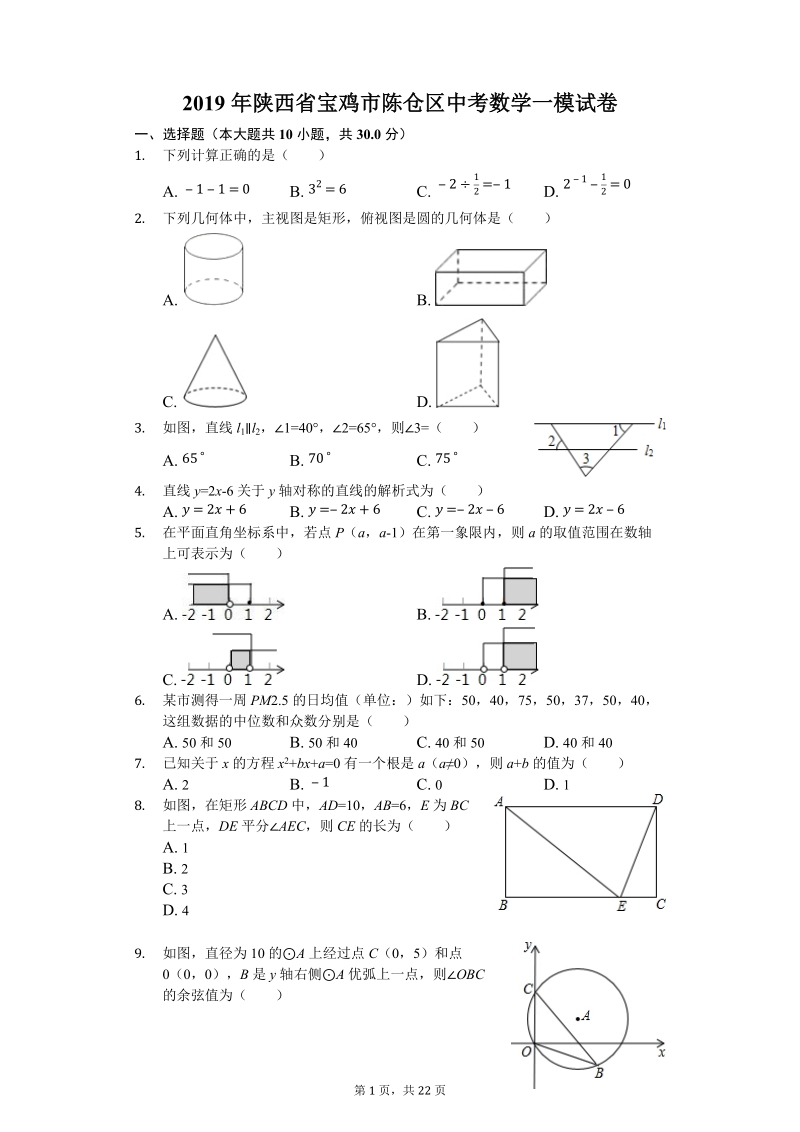
1、第 1 页，共 22 页2019 年陕西省宝鸡市陈仓区中考数学一模试卷一、选择题（本大题共 10 小题，共 30.0 分）1. 下列计算正确的是（ ）A. B. C. D. 11=0 32=6 212=1 2112=02. 下列几何体中，主视图是矩形，俯视图是圆的几何体是（ ）A. B. C. D. 3. 如图，直线 l1l2， 1=40，2=65，则3= （ ）A. B. C. D. 65 70 75 854. 直线 y=2x-6 关于 y 轴对称的直线的解析式为（ ）A. B. C. D. =2+6 =2+6 =26 =265. 在平面直角坐标系中，若点 P（a，a-1）在第一象限内，则
2、a 的取值范围在数轴上可表示为（ ）A. B. C. D. 6. 某市测得一周 PM2.5 的日均值（单位：）如下：50，40，75，50，37，50，40，这组数据的中位数和众数分别是（ ）A. 50 和 50 B. 50 和 40 C. 40 和 50 D. 40 和 407. 已知关于 x 的方程 x2+bx+a=0 有一个根是 a（a0），则 a+b 的值为（ ）A. 2 B. C. 0 D. 118. 如图，在矩形 ABCD 中，AD=10，AB=6，E 为 BC上一点，DE 平分 AEC，则 CE 的长为（ ）A. 1B. 2C. 3D. 49. 如图，直径为 10 的A 上经过点
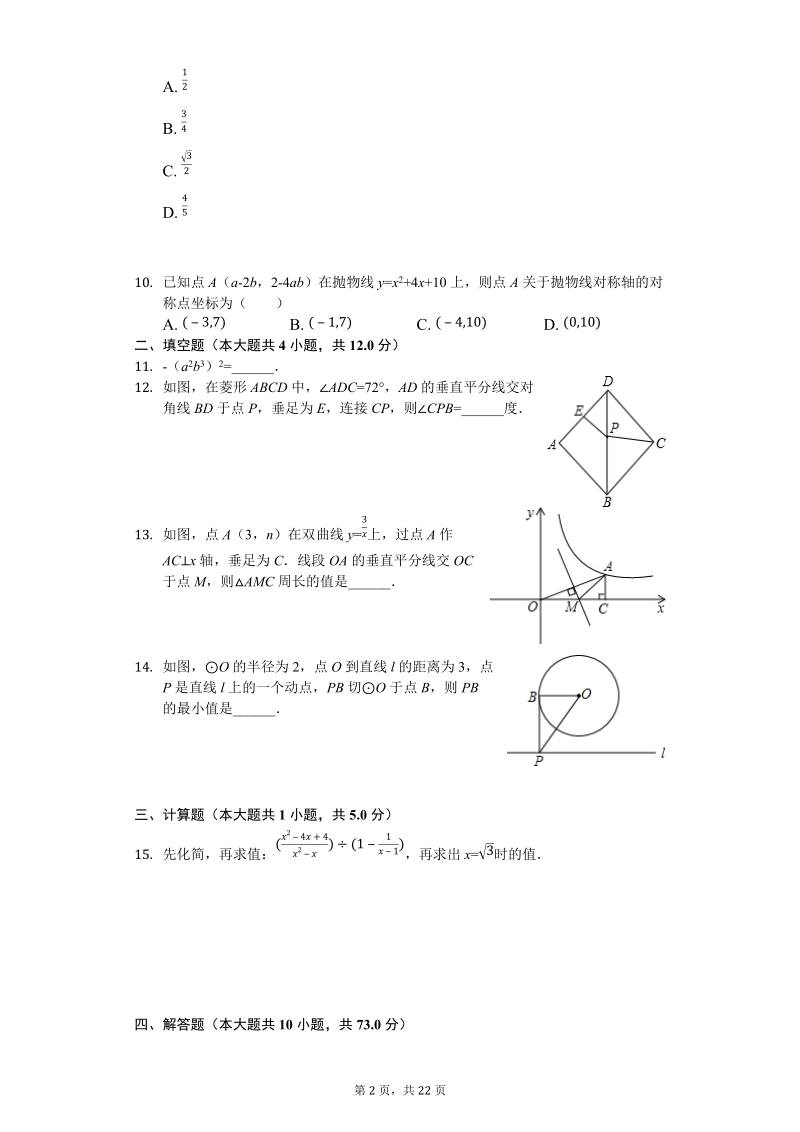
3、 C（0，5）和点0（0，0），B 是 y 轴右侧 A 优弧上一点，则 OBC的余弦值为（ ）第 2 页，共 22 页A. 12B. 34C. 32D. 4510. 已知点 A（a-2b，2-4 ab）在抛物线 y=x2+4x+10 上，则点 A 关于抛物线对称轴的对称点坐标为（ ）A. B. C. D. (3,7) (1,7) (4,10) (0,10)二、填空题（本大题共 4 小题，共 12.0 分）11. -（a 2b3） 2=_12. 如图，在菱形 ABCD 中，ADC=72，AD 的垂直平分线交对角线 BD 于点 P，垂足为 E，连接 CP，则CPB=_度13. 如图，点 A（3，n
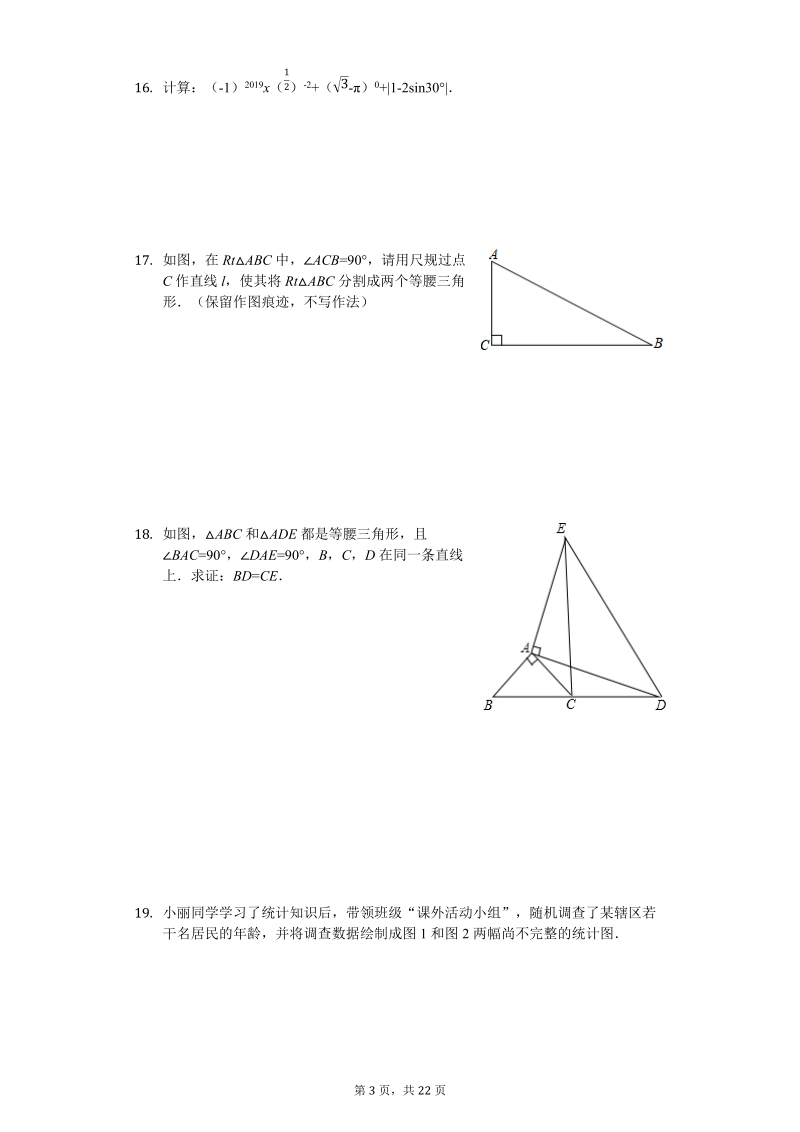
4、）在双曲线 y= 上，过点 A 作3ACx 轴，垂足为 C线段 OA 的垂直平分线交 OC于点 M，则AMC 周长的值是_14. 如图，O 的半径为 2，点 O 到直线 l 的距离为 3，点P 是直线 l 上的一个动点，PB 切O 于点 B，则 PB的最小值是_三、计算题（本大题共 1 小题，共 5.0 分）15. 先化简，再求值： ，再求出 x= 时的值(24+42)(111) 3四、解答题（本大题共 10 小题，共 73.0 分）第 3 页，共 22 页16. 计算：（-1） 2019x（ ） -2+（ -） 0+|1-2sin30|12 317. 如图，在 RtABC 中，ACB=90，
5、请用尺规过点C 作直线 l，使其将 RtABC 分割成两个等腰三角形（保留作图痕迹，不写作法）18. 如图，ABC 和ADE 都是等腰三角形，且BAC=90，DAE =90，B，C，D 在同一条直线上求证：BD=CE19. 小丽同学学习了统计知识后，带领班级“课外活动小组”，随机调查了某辖区若干名居民的年龄，并将调查数据绘制成图 1 和图 2 两幅尚不完整的统计图第 4 页，共 22 页请你根据图中的信息，解答下列问题：（1）共调查了_名居民的年龄，扇形统计图中 a=_，b=_；（2）补全条形统计图；（3）若该辖区居民约有 2600 人，请估计年龄在 1559 岁的居民人数20. 如图是某品牌
6、太阳能热水器的实物图和横断面示意图，已知真空集热管与支架 CD所在直线相交于水箱横断面O 的圆心 O，支架 CD 与水平面 AE 垂直，AB=150厘米，BAC =30，另一根辅助支架 DE=76 厘米，CED=60（1）求垂直支架 CD 的长度；（结果保留根号）（2）求水箱半径 OD 的长度（结果保留三个有效数字，参考数据： 1.414，21.73）321. 星期天 8：008：30，燃气公司给平安加气站的储气罐注入天然气，注完气之后，一位工作人员以每车 20 米 3 的加气量，依次给在加气站排队等候的若干辆车加气储气罐中的储气量 y（米 3）与时间 x（小时）的函数关系如图所示（1）8：0
7、08：30，燃气公司向储气罐注入了_米 3 的天然气；第 5 页，共 22 页（2）当 x8.5 时，求储气罐中的储气量 y（米 3）与时间 x（小时）的函数关系式；（3）正在排队等候的 20 辆车加完气后，储气罐内还有天然气_米 3，这第20 辆车在当天 9：00 之前能加完气吗？请说明理由22. 某市今年的信息技术结业考试，采用学生抽签的方式决定自己的考试内容规定：每位考生先在三个笔试题（题签分别用代码 B1、B 2、B 3 表示）中抽取一个，再在三个上机题（题签分别用代码 J1、J 2、J 3 表示）中抽取一个进行考试小亮在看不到题签的情况下，分别从笔试题和上机题中随机地各抽取一个题签（
8、1）用树状图或列表法表示出所有可能的结果；（2）求小亮抽到的笔试题和上机题的题签代码的下标（例如“B 1”的下表为“1”）均为奇数的概率23. 如图，O 的圆心在 RtABC 的直角边 AC 上，O 经过 C、D 两点，与斜边 AB交于点 E，连接 BO、ED ，有 BOED，作弦 EFAC 于 G，连接 DF（1）求证：AB 为O 的切线；（2）若 O 的半径为 5，sinDFE= ，求 EF 的长35第 6 页，共 22 页24. 如图，已知抛物线 y=ax2+bx+3 与 y 轴交于点 A，且经过 B（1，0），C（5，8）两点，点 D 是抛物线顶点， E 是对称轴与直线 AC 的交点，
9、F 与 E 关于点 D 对称（1）求抛物线的解析式；（2）求证：AFE=CFE ；（3）在抛物线的对称轴上是否存在点 P，使 AFP 与 FDC 相似？若有，请求出所有符合条件的点 P 的坐标；若没有，请说明理由25. 已知正方形 ABCD 中，E 为对角线 BD 上一点，过 E 点作 EFBD 交 BC 于 F，连接 DF，G 为 DF 中点，连接 EG，CG（1）求证：EG=CG；（2）将图中BEF 绕 B 点逆时针旋转 45，如图所示，取 DF 中点 G，连接EG，CG问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图中BEF 绕 B 点旋转任意角度，如图
10、 所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）第 7 页，共 22 页第 8 页，共 22 页答案和解析1.【答案】D【解析】解：A、 -1-1=-2，故本选项错误；B、32=9，故本选项错误；C、-2 =-22=-4，故本选项错误；D、2-1- = - =0，故本 选项 正确故选：D根据有理数计算的法则对各选项进行逐一计算即可本题考查的是负整数指数幂，熟知负整数指数幂的运算法则是解答此题的关键2.【答案】A【解析】解：A、主 视图为 矩形，俯 视图为圆，故选项正确； B、主视图为矩形，俯视图为矩形，故 选项错误； C、主视图为等腰三角形，俯
11、视图为带有圆心的圆，故选项错误； D、主视图为矩形，俯 视图为三角形，故选项错误 故选：A主视图、俯视图是分别从物体正面和上面看，所得到的图形本题考查了三视图的定义考查学生的空间想象能力3.【答案】C【解析】解：直 线 l1l2，1=40，ABC=1=40，2=65，BAC=2=45，3=180-ABC-BAC=180-40-65=75故选：C 先根据平行线的性质得出ABC 的度数，再由 对顶 角相等求出BAC 的度数，第 9 页，共 22 页根据三角形内角和定理即可求出3 的度数本题考查的是平行线的性质，解答此类题目时往往用到三角形内角和等于180这一隐藏条件4.【答案】C【解析】解：可从直
12、线 y=2x-6 上找两点：（0，-6）、（3， 0）这两个点关于 y 轴的对称点是（0，-6）（-3，0），那么这两个点在直线 y=2x-6 关于 y 轴对称的直线 y=kx+b 上，则 b=-6，-3k+b=0 解得：k=-2 y=-2x-6 故选：C 找到原直线解析式上的关于相应的坐标轴对称的点本题考查了一次函数图象的几何变换，难度不大，要注意轴对称的性质5.【答案】D【解析】解：点 P（a，a-1）在第一象限内， ，解得 a1，在数轴上可表示为，故选：D根据第一象限内点的坐标符号为（+，+）可得 ，再解不等式，在数轴上表示出 a 的取 值范围即可此题主要考查了在数轴上表示不等式的取值范
13、围，在表示解集时“”，“”要用实心圆点表示；“ ” ，“ ”要用空心圆点表示6.【答案】A【解析】第 10 页，共 22 页解：从小到大排列此数据为：37、40、 40、50、50、50、75，数据 50 出现了三次最多，所以 50 为众数； 50 处在第 4 位是中位数 故选：A找中位数要把数据按从小到大的顺序排列，位于最中间的一个数或两个数的平均数为中位数；众数是一组数据中出现次数最多的数据，注意众数可以不止一个本题属于基础题，考查了确定一组数据的中位数和众数的能力一些学生往往对这个概念掌握不清楚，计算方法不明确而误选其它选项，注意将一组数据按照从小到大（或从大到小）的顺序排列，如果数据的
14、个数是奇数，则处于中间位置的数就是这组数据的中位数如果这组数据的个数是偶数，则中间两个数据的平均数就是这组数据的中位数7.【答案】B【解析】解：把 x=a 代入 x2+bx+a=0 得 a2+ab+a=0， 所以 a+b+1=0， 所以 a+b=-1 故选：B 根据一元二次方程的解的定义把 x=a 代入方程 x2+bx+a=0 得 a2+ab+a=0，然后两边除以 a 即可得到 a+b 的值本题考查了一元二次方程的解：能使一元二次方程左右两边相等的未知数的值是一元二次方程的解8.【答案】B【解析】解：四 边形 ABCD 是矩形，ADBC，DEC=ADE，又DEC=AED，ADE=AED，AE=
15、AD=10，第 11 页，共 22 页在直角ABE 中，BE= = =8，CE=BC-BE=AD-BE=10-8=2故选：B 根据平行线的性质以及角平分线的性质证明ADE=AED，根据等角对等边，即可求得 AE 的长，在直角ABE 中，利用勾股定理求得 BE 的长，则 CE 的长即可求解本题是平行四边形的性质，以及勾股定理，等腰三角形的判定定理：等角对等边，正确求得 AE 的长是关键9.【答案】C【解析】解：如图，延长 CA 交A 与点 D，连接 OD， ，同弧所对的圆周角相等，OBC=ODC，CD 是 A 的直径，COD=90，cosODC= = = ，cosOBC= ，即 OBC 的余弦值
16、为 故选：C 首先根据圆周角定理，判断出 OBC=ODC；然后根据 CD 是A 的直径，判断出 COD=90，在 RtCOD 中，用 OD 的长度除以 CD 的长度，求出ODC的余弦值为多少，进而判断出 OBC 的余弦值为多少即可（1）此题主要考查了圆周角定理的应用，要熟练掌握，解答此题的关键是要明确：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆第 12 页，共 22 页心角的一半（2）此题还考查了特殊角的三角函数值的求法，要熟练掌握10.【答案】D【解析】解：点 A（a-2b，2-4ab）在抛物 线 y=x2+4x+10 上，（a-2b）2+4（a-2b）+10=2-4a
17、b，a2-4ab+4b2+4a-8b+10=2-4ab，（a+2）2+4（b-1）2=0，a+2=0，b-1=0，解得 a=-2，b=1，a-2b=-2-21=-4，2-4ab=2-4（-2）1=10，点 A 的坐标为（-4，10），对称轴为 直线 x=- =-2，点 A 关于对称轴的对称点的坐标为（0， 10）故选：D把点 A 坐标代入二次函数解析式并利用完全平方公式整理，然后根据非负数的性质列式求出 a、b，再求出点 A 的坐标，然后求出抛物线的对称轴，再根据对称性求解即可本题考查了二次函数图象上点的坐标特征，二次函数的对称性，坐标与图形的变化-对称，把点的坐标代入抛物线解析式并整理成非负
18、数的形式是解题的关键11.【答案】-a 4b6【解析】解：原式=-a 4b6， 故答案为-a 4b6根据积的乘方以及幂的乘方进行计算即可第 13 页，共 22 页本题考查了幂的乘方和积的乘方，掌握幂的乘方和积的乘方的运算法则是解题的关键12.【答案】72【解析】解：先连接 AP，由四边形 ABCD 是菱形， ADC=72，可得 BAD=180-72=108，根据菱形对角线平分对角可得：ADB= ADC= 72=36，ABD=ADB=36 度EP 是 AD 的垂直平分线，由垂直平分线的对称性可得DAP= ADB=36，PAB=DAB-DAP=108-36=72 度在BAP 中， APB=180-
19、BAP-ABP=180-72-36=72 度由菱形对角线的对称性可得CPB=APB=72 度欲求 CPB，可根据菱形、线段垂直平分线的性质、对称等方面去寻求解答方法本题开放性较强，解法有多种，可以从菱形、线段垂直平分线的性质、对称等方面去寻求解答方法，在这些方法中，最容易理解和表达的应为对称法， 这也应该是本题考查的目的灵活应用菱形、垂直平分线的对称性，可使解 题过程更为简便快捷13.【答案】4【解析】解：点 A（3，n）在双曲线 y= 上，n= =1，A（3，1），OC=3，AC=1OA 的垂直平分线交 OC 于 M，AM=OM，AMC 的周长=AM+MC+AC=OM+MC+AC=OC+AC
20、=3+1=4故答案为：4先求出点 A 的坐标，根据点的坐 标的定义得到 OC=3，AC=1，再根据线段垂第 14 页，共 22 页直平分线的性质可知 AM=OM，由此推出 AMC 的周长=OC+AC本题主要考查了反比例函数的图象性质和线段中垂线的性质，将求 AMC 的周长转换成求 OC+AC 是解题的关键14.【答案】 5【解析】解：PB 切O 于点 B，OBP=90，PB2=OP2-OB2，而 OB=2，PB2=OP2-4，即 PB= ，当 OP 最小时，PB 最小，点 O 到直线 l 的距离为 3，OP 的最小值为 3，PB 的最小值为 = 故答案为： 因为 PB 为切线，所以OPB 是
21、Rt又 OB 为定值，所以当 OP 最小时， PB最小根据垂线段最短，知 OP=3 时 PB 最小根据勾股定理得出 结论即可此题综合考查了切线的性质及垂线段最短等知识点，如何确定 PB 最小时点P 的位置是解 题的关键， 难度中等偏上15.【答案】解： (24+42)(111)=(2)2(1)111=(2)2(1)12= ，2当 x= 时，原式= = 3323 3233【解析】根据分式的除法和减法可以化简题目中的式子，然后将 x 的值代入化简后的第 15 页，共 22 页式子即可解答本题本题考查分式的化简求值，解答本题的关键是明确分式化简求值的方法16.【答案】解：原式=-14+1+0 =-3
22、【解析】直接利用负指数幂的性质以及绝对值的性质和特殊角的三角函数值分别化简得出答案此题主要考查了实数运算，正确化简各数是解题关键17.【答案】解如图所示：，ACD 和CDB 即为所求【解析】作斜边 AB 的中垂线可以求得中点 D，连接 CD，根据直角三角形斜边上的中线等于斜边的一半，可得 CD= AD=DB此题主要考查了应用设计与作图，关键在于用中垂线求得中点和运用直角三角形中，斜边上的中线等于斜边的一半，把 RtABC 分割成两个等腰三角形18.【答案】证明：ABC 和ADE 都是等腰直角三角形AD=AE，AB =AC，又EAC=90+ CAD，DAB=90+ CAD，DAB=EAC，在 A
23、DB 和AEC 中ADBAEC（SAS）， =BD=CE【解析】求出 AD=AE，AB=AC，DAB=EAC，根据 SAS 证出 ADBAEC 即可第 16 页，共 22 页本题考查了等腰直角三角形性质，全等三角形的性质和判定的应用，关键是推出ADB AEC19.【答案】200 25% 10%【解析】解：（1）根据“15 到 40”的百分比 为 45%，频数为 90 人，可求总数为9045%=200，a= 100%=25%，b%=1-45%-20%-25%=10%；故 a=25%，b=10%；（2）作图如下：；（3）年龄在 1559 岁的居民人数约为：2600（45%+20%）=1690 （人
24、）（1）根据“15 40”的百分比和 频数可求总数， 进而求出 b 的值，最后求出 a；（2）利用总数和百分比求出频数再补全条形图；（3）用样本估计总体即可本题考查的是条形统计图和扇形统计图的综合运用读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键条形统计图能清楚地表示出每个项目的数据；扇形统计图中各部分占总体的百分比之和为 1，直接反映部分占总体的百分比大小20.【答案】解：（1）DE=76 厘米，CED=60，sin60= = ，76CD=38 cm3第 17 页，共 22 页（2）设水箱半径 OD 的长度为 x 厘米，则 CO=（38 +x）厘米，AO=（150+x）厘米，3B
25、AC=30，CO= AO，1238 +x= （150+ x），312解得：x=150-76 =150-131.4818.5cm3【解析】（1）首先弄清题意，了解每条线段的长度与线段之间的关系，在 CDE 中利用三角函数 sin60= ，求出 CD 的长（2）首先设出水箱半径 OD 的长度为 x 厘米，表示出 CO，AO 的长度，根据直角三角形的性质得到 CO= AO，再代入数 计算即可得到答案此题主要考查了解直角三角形的应用，充分体现了数学与实际生活的密切联系，做题的关键是表示出线段的长后，理清 线段之间的关系21.【答案】8000 9600【解析】解：（1）根据图象可得出：燃气公司向储气罐注
26、入了 10000-2000=8000（米 3）的天然气；故答案为：8000；（2）当 x8.5 时由图象可设 y 与 x 的函数关系式为 y=kx+b，由已知得：，解得 ，故当 x8.5 时，储气罐中的储气量 y（米 3）与时间 x（小时）的函数关系式为：y=-1000x+18500，（3）根据每车 20 米 3 的加气量，则 20 辆车加完气后，储气罐内还有天然气：10000-2020=9600（米 3），故答案为：9600，根据题意得出：第 18 页，共 22 页9600=-1000x+18500，x=8.9 9，答：这第 20 辆车在当天 9：00 之前能加完气（1）根据函数图象可知，8
27、 点时储气罐中有 2000 米 3 的天然气，8：30 时储气罐中有 10000 米 3 的天然气，即可得出燃气公司向储气罐注入了 8000 米 3 的天然气；（2）根据图象上点的坐标得出函数解析式即可；（3）根据每车 20 米 3 的加气量，则可求出 20 辆车加完气后的储气量，进而得出所用时间此题主要考查了一次函数的应用以及待定系数法求一次函数解析式，利用图象获取正确信息是解题关键22.【答案】解：（1）；（2）共有 9 种情况，下标均为奇数的情况数有 4 种情况，所以所求的概率为 49【解析】（1）分 2 步实验列举出所有情况即可； （2）看小亮抽到的笔试题和上机题的题签代码的下标均为奇
28、数的情况数占总情况数的多少即可考查概率的求法；用到的知识点为：概率=所求情况数与总情况数之比得到笔试题和上机题的题签代码的下标均为奇数的情况数是解决本题的关键23.【答案】（1）证明：连接 OEEDOB，1=2，3=OED 又 OE=OD，2=OED，1=3又 OB=OB，OE=OC，BCOBEO（SAS）BEO=BCO=90，即 OEABAB 是O 切线第 19 页，共 22 页（2）解：连接 CE，F=4，CD=2OC =10；由于 CD 为O 的直径， 在 RtCDE 中有：ED=CDsin4=CDsinDFE= 1035=6 =22=10262=8在 RtCEG 中， ，=4=35EG
29、= 358=245根据垂径定理得： =2=485【解析】（1）连接 OE，证 OEAB 即可通过证明 BOCBOE 得证； （2）根据垂径定理，EF=2EG，所以求出 EG 的长即得解连接 CE，则CED=90，ECD=FCD=10根据三角函数可求 EG 得解此题考查了切线的判定、垂径定理及解直角三角形等知识点，综合性很强，难度较大24.【答案】解：（1）将点 B（1，0），C（5，8）代入 y=ax2+bx+3 得，+3=025+5+3=8解得 ，=1=4所以抛物线的解析式为 y=x2-4x+3；（2）由（1）可得抛物线顶点 D（2，-1 ），直线 AC 的解析式为 y=x+3，由 E 是对
30、称轴与直线 AC 的交点，则 E（2，5），由 F 与 E 关于点 D 对称，则 F（2，-7 ），证法一：从点 A、C 分别向对称轴作垂线 AM、CN，交对称轴于 M、N，在 RtFAM 和 RtFCN 中AMF=CNF=90， = = = =21015315所以 RtFAMRtFCN，所以AFE=CFE；证法二：直线 AF 的解析式为 y=-5x+3，点 C（5，8）关于对称轴的对称点是 Q（-1，8），将点 Q（-1，8）代入 y=-5x+3，可知点 Q 在直线 AF上，所以AFE=CFE；第 20 页，共 22 页（3）在FDC 中，三内角不等，且 CDF 为钝角若点 P 在点 F 下
31、方时，在AFP 中，AFP 为钝角因为AFE=CFE， AFE+AFP=180， CFE+CDF180，所以AFP 和CDF 不相等所以，点 P 在点 F 下方时，两三角形不能相似 若点 P 在点 F 上方时，由AFE=CFE，要使AFP 与FDC 相似只需 = （点 P 在 DF 之间）或 = （点 P 在 FD 的延长线上） 解得点 P 的坐标为（2，-3）或（ 2，19）【解析】（1）已知抛物线过 B、C 两点，而且两点的坐标都已得出，可用待定系数法来求函数的解析式； （2）由（1）可得抛物线顶点 D（2，-1），直 线 AC 的解析式 为 y=x+3，由 E 是对称轴与直线 AC 的交
32、点，可得 E 点坐标，由 F 与 E 关于点 D 对称，可得 F 点坐标，从点 A、C 分别向对称轴作垂线 AM、CN，交对称轴于 M、N，通过证明 RtFAMRtFCN，根据相似三角形的性 质即可求解； （3）在FDC 中，三内角不等，且CDF 为钝角，分两种情况：若点 P 在点F 下方时， 若点 P 在点 F 上方时，讨论即可求解主要考查待定系数法、方程、函数及三角形相似等知识，考 查综合运用数学知识、分析问题、解决问题的能力，考 查数形结合、分类讨论的思想此题是一道以函数为背景的综合压轴题，第 1、2 两个小题较为容易，上手很 轻松，第 3 小题中很容易看出要讨论相似三角形的对应顶角，想
33、提醒大家的是在中考中应该对可能的情况进行逐一讨论，才能尽量防止漏解25.【答案】（1）证明：四边形 ABCD 是正方形，DCF=90，在 RtFCD 中，G 为 DF 的中点，CG= FD，12同理，在 RtDEF 中，EG= FD，12CG=EG第 21 页，共 22 页（2）解：（1）中结论仍然成立，即 EG=CG证法一：连接 AG，过 G 点作 MNAD 于 M，与 EF 的延长线交于 N 点在DAG 与 DCG 中，AD=CD， ADG=CDG，DG=DG，DAGDCG（SAS），AG=CG；在DMG 与 FNG 中，DGM=FGN，FG =DG，MDG =NFG，DMGFNG（ASA
34、 ），MG=NG；EAM=AEN=AMN=90，四边形 AENM 是矩形，在矩形 AENM 中，AM =EN，在AMG 与ENG 中，AM=EN，AMG= ENG，MG=NG，AMGENG（SAS），AG=EG，EG=CG证法二：延长 CG 至 M，使 MG=CG，连接 MF，ME，EC，在DCG 与 FMG 中，FG=DG，MGF =CGD，MG=CG，DCGFMGMF=CD，FMG=DCG，MFCDAB，EFMF在 RtMFE 与 RtCBE 中，MF=CB，MFE= EBC，EF= BE，MFECBEMEF=CEBMEC=MEF+FEC=CEB+CEF=90，MEC 为直角三角形MG=C
35、G，EG= MC，12EG=CG（3）解：（1）中的结论仍然成立理由如下：过 F 作 CD 的平行线并延长 CG 交于 M 点，连接 EM、EC，过 F 作 FN 垂直于 AB 于 N由于 G 为 FD 中点，易证CDGMFG，得到 CD=FM，又因为 BE=EF，易证 EFM=EBC，则 EFMEBC，FEM=BEC，EM=ECFEC+BEC=90，FEC +FEM=90，即MEC=90，MEC 是等腰直角三角形，第 22 页，共 22 页G 为 CM 中点，EG=CG，EG CG【解析】（1）利用直角三角形斜边上的中线等于斜边的一半，可证出 CG=EG （2）结论仍然成立，连接 AG，过 G 点作 MNAD 于 M，与 EF 的延长线交于N 点；再证明DAGDCG，得出 AG=CG；再证出 DMGFNG，得到MG=NG；再证 明 AMGENG，得出 AG=EG；最后证出 CG=EG （3）结论依然成立还知道 EGCG本题利用了直角三角形斜边上的中线等于斜边的一半的性质、全等三角形的判定和性质
