1、第 1页，共 14页2019 年南通市中考数学押题预测卷注意：本试卷包含、两卷。第卷为选择题，所有答案必须用 2B铅笔涂在答题卡中相应的位置。第卷为非选择题，所有答案必须填在答题卷的相应位置。答案写在试卷上均无效，不予记分。 总分：150分 考试时间：120分钟一、选择题（本大题共15小题，共30.0分）1. 某种计算机完成一种疾病运算所需的时间约为 0.0000000003秒，试用科学记数法表示该数（ ）A.0.310-9 B.0.310-10 C.310-10 D.310-92. 下列计算正确的是（ ）A. a2a3=a6 B.2a3a=6aC. （ a2） 3=a6 D. （ a+b）
2、2=a2+b23. 不等式 5x-1 2x+5的解集在数轴上表示正确的是（）A. B.C. D.4. 如图，菱形 ABCD 的周长为 28，对角线 AC， BD 交于点 O， E 为 AD 的中点，则OE 的长等于（）A.2B.3.5C.7D.145. 已知一次函数 y=（ k-2） x-m 的图象与 y 轴的负半轴相交，且函数值 y 随自变量 x的增大而减小，则下列结论正确的是（ ）A. k 2， m 0 B. k 2， m 0 C. k 2， m 0 D. k 0， m 06. 某小组长统计组内 5人一天在课堂上的发言次数分別为 3， 3， 0， 4， 5关于这组数据，下列说法错误的是（
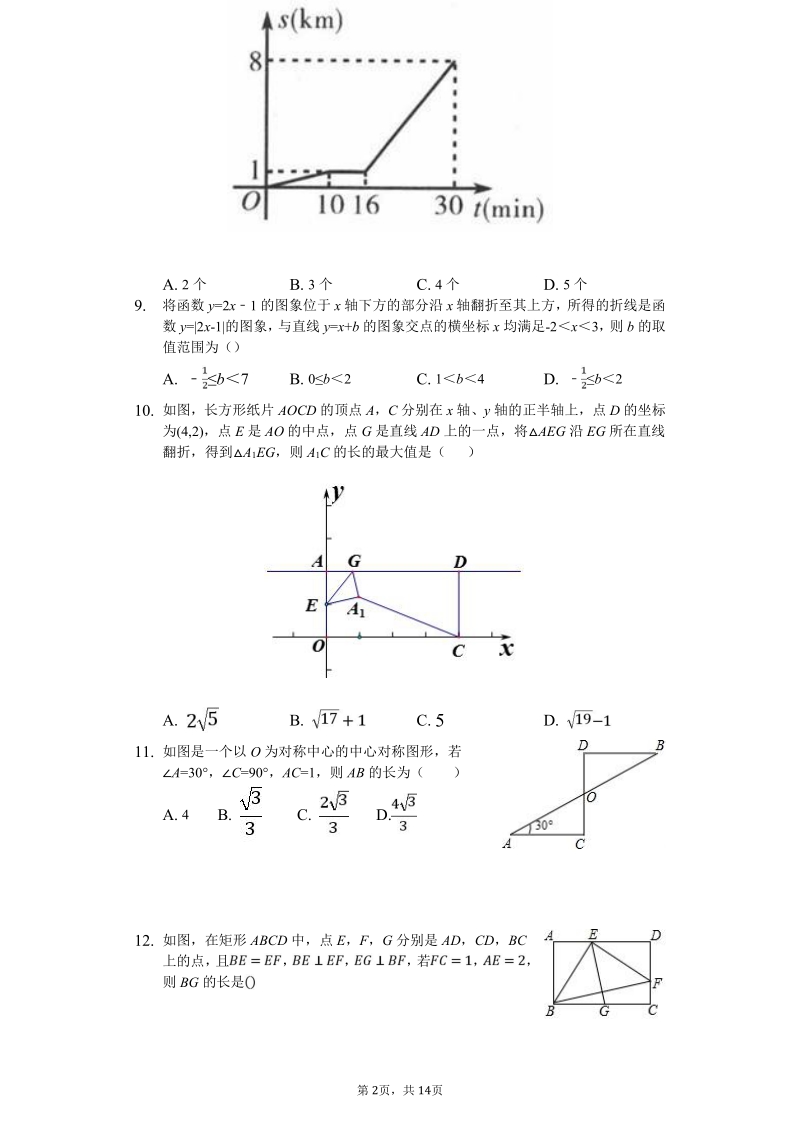
3、）A. 众数是 3 B. 中位数是 0 C. 平均数 3 D. 方差是 2.87. 五根小木棒的长度分别为 3cm,5cm,8cm,12cm,13cm 任选三根组成三角形，组成直角三角形的概率为（）A. B. C. D.8. 如图所示，小亮从家出发步行到公交车站，等公交车，最后坐公交车到达学校，图中的折线表示小亮的行程 s(km)与所花时间 t(min)之间的函数关系下列说法：学校和小亮家的路程为 8km；小亮等公交车的时间为 6min；小亮步行的速度是 100m/min；公交车的速度是 350m/min；小亮从家出发到学校共用了 24min其中正确的有 ()第 2页 ， 共 14页A.2个
4、B.3个 C.4个 D.5个9. 将 函 数 y=2x 1的 图 象 位 于 x 轴 下 方 的 部 分 沿 x 轴 翻 折 至 其 上 方 ， 所 得 的 折 线 是 函数 y=|2x-1|的 图 象 ， 与 直 线 y=x+b 的 图 象 交 点 的 横 坐 标 x 均 满 足 -2 x 3， 则 b 的 取值 范 围 为 （ ）A. b 7 B.0b 2 C.1 b 4 D. b 210. 如 图 ， 长 方 形 纸 片 AOCD 的 顶 点 A， C 分 别 在 x 轴 、 y 轴 的 正 半 轴 上 ， 点 D 的 坐 标为 (4,2)， 点 E 是 AO 的 中 点 ， 点 G 是
5、 直 线 AD 上 的 一 点 ， 将 AEG 沿 EG 所 在 直 线翻 折 ， 得 到 A1EG， 则 A1C 的 长 的 最 大 值 是 （ ）A. B. C.5 D.11. 如 图 是 一 个 以 O 为 对 称 中 心 的 中 心 对 称 图 形 ， 若 A=30， C=90， AC=1， 则 AB 的 长 为 （ ）A.4 B. C. D.12. 如 图 ， 在 矩 形 ABCD 中 ， 点 E， F， G 分 别 是 AD， CD， BC上 的 点 ， 且 ， ， ， 若 ， ，则 BG 的 长 是第 3页，共 14页A. B. C. D.13. 若 ，则直线 y=kx+2k 一
6、定经过第（ ）象限 .A. 一、二 B. 二、三 C. 三、四 D. 一14. 如图所示，在矩形 ABCD 中， F 是 DC 上一点， AE 平分 BAF交 BC 于点 E，且 DEAF，垂足为点 M， BE=3， AE=2 ，则MF 的长是（ ）A. B. C.1 D.15. 如图，在四边形 ABCD 中， A=60， B= D=90， BC=2， CD=3，则 AB=（ ）A.4 B.5 C. D.二、填空题（本大题共10小题，共30.0分）16. 在实数范围内分解因式： 2x2y 4y=_17. 若式子 有意义，则 x 的取值范围为 _18. 将一副三角尺如图所示叠放在一起，如果 AB
7、=10cm，那么 AF=_cm19. 如下图， RtABC 中， C=90， AC=4， BC=9，分别以它的三边为直径向上作三个半圆，则图中阴影部分的面积是20. 有五张分别印有圆、等腰三角形、矩形、菱形、正方形图案的卡片（卡片中除图案不同外，其余均相同），现将有图案的一面朝下任意摆放，从中任意抽取一张，抽到有中心对称图案的卡片的概率是 _。21. 如果一组数据 3， x， 1， 2， 5的平均数是 3，那么方差是 _22. 如图，在同一平面直角坐标系中作出相应的两个一次函数的图象，则不等式组 的解集为 _.第 4页 ， 共 14页23. 如 图 ， OAC 和 BAD 都 是 等 腰 直
8、角 三 角 形 ， ACO= ADB=90， 反 比 例 函 数 y= 在 第 一 象 限 的 图 象经 过 点 B 若 OA2-AB2=12， 则 k 的 值 为 _24. 如 图 ， 在 平 面 直 角 坐 标 系 中 ， M 为 y 轴 正 半 轴 上 一 点 ， 过 点 M 的 直 线 lx 轴 ， l 分别 与 反 比 例 函 数 y= 和 y= 的 图 象 交 于 A、 B 两 点 ， 若 SAOB=3， 则 k 的 值 为 _ 25. 如 图 ， 正 方 形 ABCD 中 ， AD=4， 点 E 是 对 角 线 AC 上 一 点 ，连 接 DE， 过 点 E 作 EFED， 交
9、AB 于 点 F， 连 接 DF， 交AC 于 点 G， 将 EFG 沿 EF 翻 折 ， 得 到 EFM， 连 接 DM，交 EF 于 点 N， 若 点 F 是 AB 边 的 中 点 ， 则 EMN 的 周 长 是_三、计算题（本大题共3小题，共18.0分）26. （ 1） 计 算 ： （ - ） -（ + ） ；（ 2） 计 算 （ 2 - ） 2+（ +2 ） 27. 先 化 简 ， 再 求 值 ： （ x+2） 2+（ 2x+1） （ 2x-1） -4x（ x+1） ， 其 中 x=228. 如 图 ， D 是 ABC 的 边 AB 上 一 点 ， 连 接 CD， 若 AD=2，BD=
10、4， ACD= B， 求 AC 的 长 四、解答题（本大题共9小题，共72.0分）29. 下 表 是 随 机 抽 取 的 某 公 司 部 分 员 工 的 月 收 入 资 料 月 收 入 /元 45000 18000 10000 5500 5000 3400 3000 2000人 数 1 1 1 3 6 1 11 2（ 1） 请 计 算 以 上 样 本 的 平 均 数 和 中 位 数 ；（ 2） 甲 乙 两 人 分 别 用 样 本 平 均 数 和 中 位 数 来 估 计 推 断 公 司 全 体 员 工 月 收 入 水 平 ，请 你 写 出 甲 乙 两 人 的 推 断 结 论；（ 3） 指 出 谁
11、 的 推 断 比 较 科 学 合 理 ， 能 真 实 地 反 映 公 司 全 体 员 工 月 收 入 水 平 ， 并 说出 另 一 个 人 的 推 断 依 据 不 能 真 实 反 映 公 司 全 体 员 工 月 收 入 水 平 的 原 因 第 5页，共 14页30. 如图，已知 CD 平分 ACB， 1= 2（ 1）求证： DEAC；（ 2）若 3=30， B=25，求 BDE 的度数31. 如图，在 O 中， DE 是 O 的直径， AB 是 O 的弦， AB的中点 C 在直径 DE 上已知 AB=8cm， CD=2cm（ 1）求 O 的面积；（ 2）连接 AE，过圆心 O 向 AE 作垂线
12、，垂足为 F，求 OF的长32. 为了落实党的“精准扶贫”政策， A、 B 两城决定向 C、 D 两乡运送肥料以支持农村生产，已知 A、 B 两城共有肥料 500吨，其中 A 城肥料比 B 城少 100吨，从 A 城往 C、 D 两乡运肥料的费用分别为 20元 /吨和 25元 /吨；从 B 城往 C、 D 两乡运肥料的费用分别为 15元 /吨和 24元 /吨现 C 乡需要肥料 240吨， D 乡需要肥料 260吨（ 1） A 城和 B 城各有多少吨肥料？（ 2）设从 A 城运往 C 乡肥料 x 吨，总运费为 y 元，求出最少总运费（ 3）由于更换车型，使 A 城运往 C 乡的运费每吨减少 a（
13、 0 a 6）元，这时怎样调运才能使总运费最少？33. A， B 两地相距 60km，甲、乙两人从两地出发相向而行，甲先出发图中 l1， l2表示两人离 A 地的距离 s（ km）与时间 t（ h）的关系，请结合图象解答下列问题：（ 1）表示乙离 A 地的距离与时间关系的图象是_ （填 l1或 l2）；甲的速度是_km/h，乙的速度是 _km/h；（ 2）甲出发多少小时两人恰好相距 5km？34. 如图，抛物线 y=-x2+bx+c 经过 A（ -1， 0）， B（ 3， 0）两点，且与 y 轴交于点 C，点 D 是抛物线的顶点，抛物线的对称轴 DE 交 x 轴于点 E，连接 BD（ 1）求经
14、过 A， B， C 三点的抛物线的函数表达式；（ 2）点 P 是线段 BD 上一点，当 PE=PC 时，求点 P 的坐标；（ 3）在（ 2）的条件下，过点 P 作 PFx 轴于点 F， G 为抛物线上一动点， M 为 x轴上一动点， N 为直线 PF 上一动点，当以 F、 M、 N、 G 为顶点的四边形是正方形第 6页 ， 共 14页时 ， 请 求 出 点 M 的 坐 标 35. 已 知 ： 如 图 ， 在 中 ， ， ， 点 P 由 B 出 发 沿BA 方 向 向 点 A 匀 速 运 动 ， 速 度 为 1cm/s； 点 Q 由 A 出 发 沿 AC 方 向 向 点 C 匀 速 运动 ， 速
15、 度 为 2cm/s； 连 接 PQ 若 设 运 动 的 时 间 为 ts（ ） ， 解 答 下 列 问 题 ：（ 1） 当 为 何 值 时 ， ？（ 2） 设 的 面 积 为 y（ ） ， 求 y 与 t 之 间 的 函 数 关 系 式 ；（ 3） 如 图 ， 连 接 PC， 并 把 沿 QC 翻 折 ， 得 到 四 边 形 ， 那 么 是 否 存在 某 一 时 刻 t， 使 四 边 形 为 菱 形 ？ 若 存 在 ， 求 出 此 时 的 值 ； 若 不 存 在 ， 说 明理 由 36. 在 平 面 直 角 坐 标 系 中 ， 点 A（ m， m） 在 第 一 象 限 ， 且 实 数 m 满
16、 足 条 件 ： |-m|=m- ， ABy 轴 于 B， ACx 轴 于 C（ 1） 求 m 的 值 ；（ 2） 如 图 1， BE=1， 连 接 AE， 过 A 作 AFAE 交 x 轴 于 F， 连 接 EF， D 在 AO 上 ，且 AD=AE， 连 接 ED 并 延 长 交 x 轴 于 点 P， 求 点 P 的 坐 标 ；（ 3） 如 图 2， G 为 线 段 OC 延 长 线 上 一 点 ， AC=CG， E 为 线 段 OB 上 一 动 点 （ 不 与O， B 重 合 ） ， F 为 线 段 CE 的 中 点 ， 若 BFFK 交 AG 于 K， 请 问 FBK 的 大 小 是否
17、 变 化 ？ 若 不 变 ， 请 求 其 值 ； 若 改 变 ， 求 出 变 化 的 范 围 。第 7页，共 14页37. 如图，已知 ABC 中， AB=AC=12cm， BC=10cm，点 D 为 AB 的中点如果点 P 在线段 BC 上以 2cm/s 的速度由点 B 向 C 点运动，同时，点 Q 在线段 AC 上由点 A向 C 点以 4cm/s 的速度运动 （ 1）若点 P、 Q 两点分别从 B、 A 两点同时出发，经过 2秒后， BPD 与 CQP 是否全等，请说明理由；（ 2）若点 P、 Q 两点分别从 B、 A 两点同时出发， CPQ 的周长为 18cm，问：经过几秒后， CPQ
18、是等腰三角形？【答案和解析】 1-5 CDABA 6-10 BDBDB 11-15 DABDD16.2y 17. x-2且 x118.5 19.1820. 21.222.x 323.624.-225.26.解：（ 1）原式 =2 - - -= - ；（ 2）原式 =12-12 +6+ +2=18-12 +3 +2=18-7 27.解：原式 =x2+4x+4+（ 4x2-1） -（ 4x2+4x）=x2+4x+4+4x2-1-4x2-4x=x2+3，当 x=2时，原式 =22+3=728.解：在 ABC 和 ACD 中， ACD= B， A= A，ABCACD，第 8页 ， 共 14页 = 即
19、AC2=ADAB=AD（ AD+BD） =26=12，AC=2 29.解 ： （ 1） 样 本 的 平 均 数 为 ：=6150；这 组 数 据 共 有 26个 ， 第 13、 14个 数 据 分 别 是 3400、 3000，所 以 样 本 的 中 位 数 为 ： =3200（ 2） 甲 ： 由 样 本 平 均 数 6150元 ， 估 计 公 司 全 体 员 工 月 平 均 收 入 大 约 为 6150元 ；乙 ： 由 样 本 中 位 数 为 3200元 ， 估 计 公 司 全 体 员 工 约 有 一 半 的 月 收 入 超 过 3200元 ， 约 有一 半 的 月 收 入 不 足 3200
20、元 （ 3） 乙 的 推 断 比 较 科 学 合 理 由 题 意 知 样 本 中 的 26名 员 工 ， 只 有 3名 员 工 的 收 入 在 6150元 以 上 ， 原 因 是 该 样 本 数 据极 差 较 大 ，所 以 平 均 数 不 能 真 实 的 反 映 实 际 情 况 30.（ 1） 证 明 ： CD 平 分 ACB， 2= 3 1= 2， 1= 3，DEAC；（ 2） 解 ： CD 平 分 ACB， 3=30， ACB=2 3=60DEAC， BED= ACB=60 B=25， BDE=180-60-25=95（2）根 据 3=30可 得 出 ACB的 度 数 ，再 由 平 行线的
21、 性质得 出 BED的 度 数 ，由 三 角 形 内角 和 定 理 即 可 得 出结论本题考查的 是 平 行线的 判 定 与 性质，涉 及 到 角 平 分线的 定义、三 角 形 内 角 和 定 理 等 知识，难度较低 31.解 ： （ 1） 连 接 OA， 如 图 1所 示C 为 AB 的 中 点 ， AB=8cm，AC=4cm又 CD=2cm设 O 的 半 径 为 r， 则 （ r-2） 2+42=r2解 得 ： r=5S=r2=25=25（ 2） OC=OD-CD=5-2=3EC=EO+OC=5+3=8EA= = =4第 9页，共 14页EF= = =2OF= = =32.解：（ 1）设
22、A 城有化肥 a 吨， B 城有化肥 b 吨根据题意，得解得答： A 城和 B 城分别有 200吨和 300吨肥料；（ 2）设从 A 城运往 C 乡肥料 x 吨，则运往 D 乡（ 200-x）吨从 B 城运往 C 乡肥料（ 240-x）吨，则运往 D 乡（ 60+x）吨如总运费为 y 元，根据题意，则： y=20x+25（ 200-x） +15（ 240-x） +24（ 60+x）=4x+10040由于函数是一次函数， k=4 0所以当 x=0时，运费最少，最少运费是 10040元（ 3）设减少运费后，总运费为 w 元，则 w (20-a)x+25(200-x)+15(240-x)+24300
23、-(240-x) (4-a)x+10040(0x200)当 0 a 4时， 4-a 0，此时 w 随 x 的增大而增大， 当 x 0时， w 最小 10040；当 a 4时， w 10040，不管怎样调运，费用一样多，均为 10040元；当 4 a 6时， 4-a 0，此时 w 随 x 的增大而减小，当 x 200时， w最小 10840-200a4 a 6， 10840-200a 10040，使总运费最少的调运方案为：从 A 城运往 C 乡 200吨，从 A 城运往 D 乡 0吨，从 B城运往 C 乡 40吨，从 B 城运往 D 乡 260吨33.解：（ 1） l2； 30； 20；（ 2）
24、设甲出发 x 小时两人恰好相距 5km，由题意得：30x+20（ x-0.5） +5=60或 30x+20（ x-0.5） -5=60，解得 x=1.3或 1.5，答：甲出发 1.3小时或 1.5小时两人恰好相距 5km34.解：（ 1） 抛物线 y=-x2+bx+c 经过 A（ -1， 0）， B（ 3， 0）两点， ，解得， ，经过 A， B， C 三点的抛物线的函数表达式为 y=-x2+2x+3；（ 2）如图 1，连接 PC、 PE，第 10页 ， 共 14页x=- =- =1，当 x=1时 ， y=4，点 D 的 坐 标 为 （ 1， 4） ，设 直 线 BD 的 解 析 式 为 ：
25、y=mx+n，则 ，解 得 ， ，直 线 BD 的 解 析 式 为 y=-2x+6，设 点 P 的 坐 标 为 （ x， -2x+6） ，则 PC2=x2+（ 3+2x-6） 2， PE2=（ x-1） 2+（ -2x+6） 2，PC=PE，x2+（ 3+2x-6） 2=（ x-1） 2+（ -2x+6） 2，解 得 ， x=2，则 y=-22+6=2，点 P 的 坐 标 为 （ 2， 2） ；（ 3） 如 图 ： 设 点 M 的 坐 标 为 （ a， 0） ， 则 点 G 的 坐 标 为 （ a， -a2+2a+3） ，以 F、 M、 N、 G 为 顶 点 的 四 边 形 是 正 方 形 ，
26、FM=MG， 即 |2-a|=|-a2+2a+3|，当 2-a=-a2+2a+3时 ，整 理 得 ， a2-3a-1=0，第 11页，共 14页解得， a= ，当 2-a=-（ -a2+2a+3）时，整理得， a2-a-5=0，解得， a= ，当以 F、 M、 N、 G 为顶点的四边形是正方形时，点 M 的坐标为（ ， 0），（ ，0），（ ， 0），（ ， 0）35.解：（ 1）在 RtABC 中， AB= =5，由题意知： AP=5-t， AQ=2t，若 PQBC，则 APQABC， ， ，t= 所以当 t= 时， PQBC（ 2）过点 P 作 PHAC 于 HAPHABC， ， ，PH=
27、3-t ，y= AQPH= 2t(3- t)=- t2+3t第 12页 ， 共 14页即 ： y 与 t 之 间 的 函 数 关 系 式 为 y=- t2+3t.（ 3） 过 点 P 作 PMAC 于 M， PNBC 于 N，若 四 边 形 PQPC 是 菱 形 ， 那 么 PQ=PCPMAC 于 M，QM=CMPNBC 于 N， 易 知 PBNABC ， ，PN= t，QM=CM= t， t+ t+2t=4，解 得 ： t= 当 t= s 时 ， 四 边 形 PQPC 是 菱 形 36.解 ： （ 1） 有 意 义 ，m4，| -m|=m- | -m|=m- ，m- =m- ，解 得 ： m
28、=7，m 的 值 为 7（ 2） 过 点 D 作 DHx 轴 于 点 H， 如 图 1ABy 轴 ， ACx 轴 ， BOC=90， ABO= BOC= ACO=90，四 边 形 ABOC 是 矩 形 第 13页，共 14页m=7， A（ m， m），OC=AB=OB=AC=7，AO=7 BE=1， AB=7，AE= = =5 AE=AD， AD=5 ，OD=2 DHOC， ACOC，DHAC，ODHOAC， = = ，即 = = ，OH=DH=2同理可得： = ， = = ，解得： PH=1，OP=OH+PH=2+1=3，点 P 的坐标为（ 3， 0）（ 3） FBK 的大小不变过点 K 作
29、 KMAC 于点 M，过点 K 作 KNBA，交 BA 的延长线于点 N，延长 BF、 AC 交于点 Q，连接 KQ，如图 2 N= MAN= AMK=90，四边形 AMKN 是矩形AC=CG， ACG=90， CAG=45 AMK=90， AKM= CAG=45，AM=KM， 矩形 AMKN 是正方形，KM=KN， MKN=90BECQ， EBF= CQF在 BFE 和 QFC 中，BFEQFC（ AAS），BF=QFBFKF， KB=KQ在 RtBNK 和 RtQMK 中，RtBNKRtQMK（ HL）， BKN= QKM， BKQ= BKM+ QKM= BKM+ BKN= MKN=90，
30、 KBQ= KQB=45第 14页 ， 共 14页37.解 ： （ 1） BPD 与 CQP 是 全 等 理 由 如 下 ：当 P， Q 两 点 分 别 从 B， A 两 点 同 时 出 发 运 动 2秒 时有 BP=22=4cm， AQ=42=8cm则 CP=BC-BP=10-4=6cmCQ=AC-AQ=12-8=4cmD 是 AB 的 中 点BP=CQ， BD=CP又 ABC 中 ， AB=AC B= C在 BPD 和 CQP 中BPDCQP（ SAS）（ 2） 设 当 P， Q 两 点 同 时 出 发 运 动 t 秒 时 ，有 BP=2t， AQ=4tt 的 取 值 范 围 为 0 t3则 CP=10-2t， CQ=12-4tCPQ 的 周 长 为 18cm，PQ=18-（ 10-2t） -（ 12-4t） =6t-4要 使 CPQ 是 等 腰 三 角 形 ， 则 可 分 为 三 种 情 况 讨 论 ： 当 CP=CQ 时 ， 则 有 10-2t=12-4t解 得 ： t=1 当 PQ=PC 时 ， 则 有 6t-4=10-2t解 得 ： 当 QP=QC 时 ， 则 有 6t-4=12-4t解 得 ：三 种 情 况 均 符 合 t 的 取 值 范 围 综 上 所 述 ， 经 过 1秒 或 秒 或 秒 时 ， CPQ 是 等 腰 三 角 形 .
