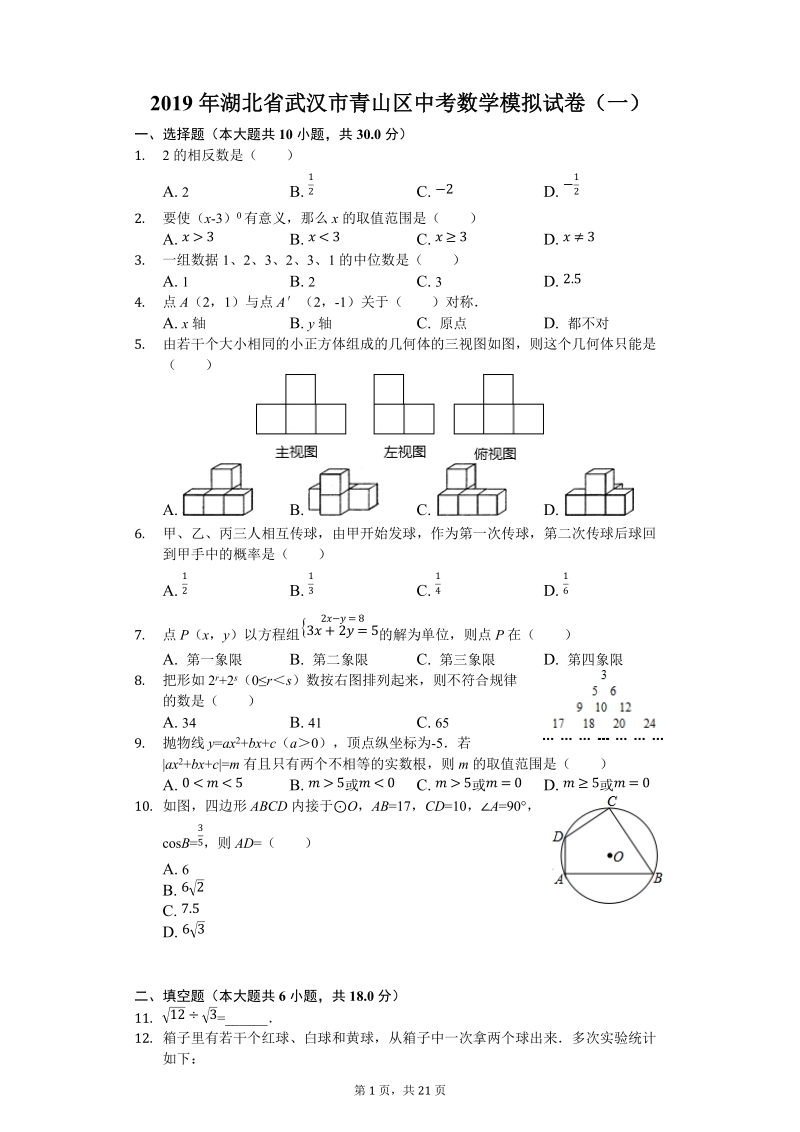
1、第 1 页，共 21 页2019 年湖北省武汉市青山区中考数学模拟试卷（一）一、选择题（本大题共 10 小题，共 30.0 分）1. 2 的相反数是（ ）A. 2 B. C. D. 12 2 122. 要使（x-3） 0 有意义，那么 x 的取值范围是（ ）A. B. C. D. 3 5 5 =0 5 =010. 如图，四边形 ABCD 内接于O ，AB=17，CD=10， A=90，cosB= ，则 AD=（ ）35A. 6B. 62C. 7.5D. 63二、填空题（本大题共 6 小题，共 18.0 分）11. =_12312. 箱子里有若干个红球、白球和黄球，从箱子中一次拿两个球出来多次实
2、验统计如下：第 2 页，共 21 页至少有一个球是白球的次数 13 20 35 71 107 146 288至少有一个球是白球的频率 0.65 0.67 0.70 0.71 0.713 0.73 0.72至少有一个球是白球的次数 13 20 35 71 107 146 288童威估计至少有一个球是白球的概率约是_（保留一位小数）13. 计算 =_421+2+114. 一个钝角三角形两边长分别为 4、5，则此三角形的最大边 c 的取值范围是为_15. 如图，双曲线 的第一象限分支上有一动点 P，点 A（-=22，-2），B （2 ，2），则 PA-PB 的值=_16. 如图，在菱形 ABCD 中
3、，ABC =120，将菱形折叠，使点 A 恰好落在对角线 BD 上的点 G 处（不与 B、D 重合），折痕为 EF，若 DG=2，BG =6，则 BE 的长为_三、计算题（本大题共 1 小题，共 8.0 分）17. 计算：8a 62a2+4a32a-（3a 2） 2四、解答题（本大题共 7 小题，共 64.0 分）18. 如图，点 E、B、C、F 在一条直线上，ABCD，AB= FB，CD= CE，AF、DE 交于 O，求EOF的度数19. 某校为了了解九年级学生体育测试成绩情况，抽取部分学生的体育测试成绩为样本，按 A、B、C、D 四个等级进行统计，并将统计结果绘制如下两幅统计图，请第 3
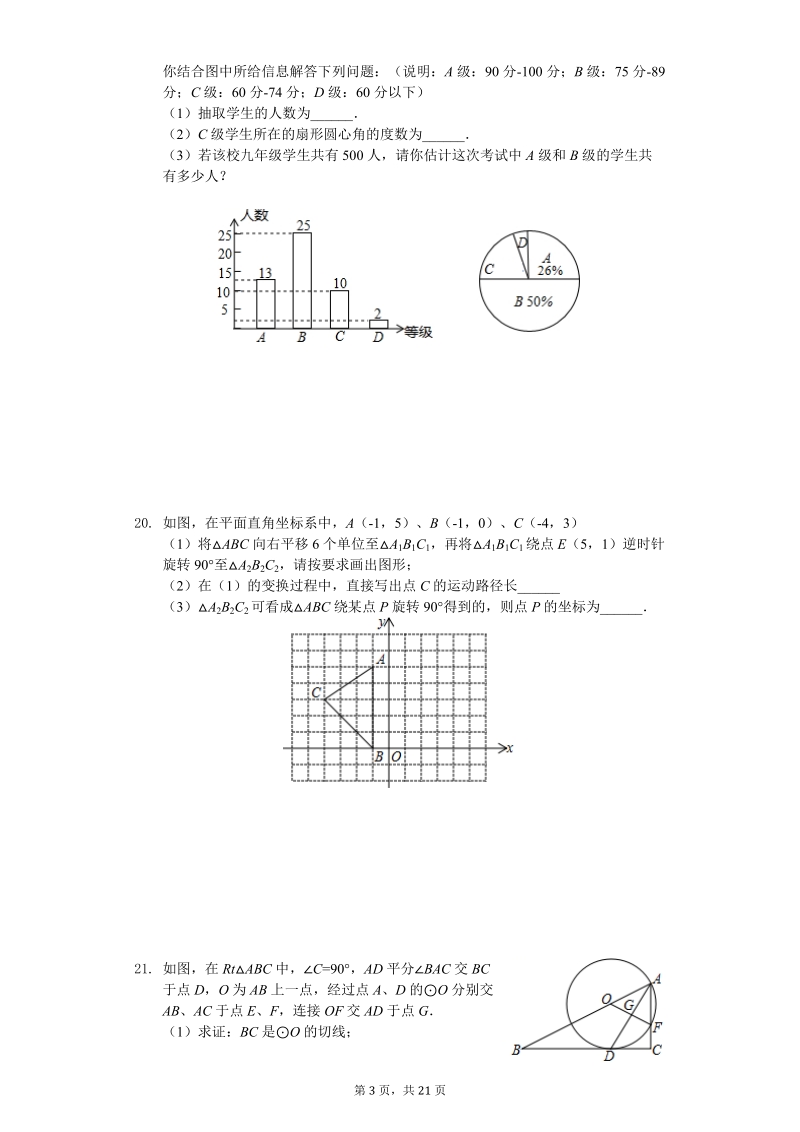
4、页，共 21 页你结合图中所给信息解答下列问题：（说明：A 级：90 分-100 分；B 级：75 分-89分；C 级：60 分-74 分；D 级： 60 分以下）（1）抽取学生的人数为_（2）C 级学生所在的扇形圆心角的度数为 _（3）若该校九年级学生共有 500 人，请你估计这次考试中 A 级和 B 级的学生共有多少人？20. 如图，在平面直角坐标系中，A（-1，5）、B（-1 ， 0）、C （-4 ，3）（1）将ABC 向右平移 6 个单位至 A1B1C1，再将A 1B1C1 绕点 E（5，1）逆时针旋转 90至 A2B2C2，请按要求画出图形；（2）在（1）的变换过程中，直接写出点 C
5、 的运动路径长_（3）A 2B2C2 可看成ABC 绕某点 P 旋转 90得到的，则点 P 的坐标为_21. 如图，在 RtABC 中，C =90，AD 平分BAC 交 BC于点 D，O 为 AB 上一点，经过点 A、D 的O 分别交AB、AC 于点 E、F，连接 OF 交 AD 于点 G（1）求证：BC 是O 的切线；第 4 页，共 21 页（2）若 BE=8，sinB= ，求： O 的半径 r；DG 的长51322. “扬州漆器”名扬天下，某网店专门销售某种品牌的漆器笔筒，成本为 30 元/ 件，每天销售 y（件）与销售单价 x（元）之间存在一次函数关系，如图所示（1）求 y 与 x 之间
6、的函数关系式；（2）如果规定每天漆器笔筒的销售量不低于 240 件，当销售单价为多少元时，每天获取的利润最大，最大利润是多少？（3）该网店店主热心公益事业，决定从每天的销售利润中捐出 150 元给希望工程，为了保证捐款后每天剩余利润不低于 3600 元，试确定该漆器笔筒销售单价的范围23. （1）如图 1，AHCG，EG CG，点 D 在 CG 上，AD CE 于点 F，求证：；=（2）在ABC 中，记 tanB=m，点 D 在直线 BC 上，点 E 在边 AB 上如图 2，m=3，点 D 在线段 BC 上，且 ADCE 于点 F，若 AD=3CE，则=_；如图 3，m= ，点 D 在线段 B
7、C 的延长线上，连接 DE 交 AC 于 M，CMD =60，33DE=2AC，CD= ，求 BE 的长33第 5 页，共 21 页24. 如图，已知抛物线 与 x 轴交于 A、B 两点（A 点在 B 点的左=122+242边），与 y 轴负半轴交于点 C（1）当 n=0 时，求 A、B、C 三点的坐标；（2）如图 1，过点 A 作 ADBC 交抛物线于另一点 D，交 y 轴交于点 E若AE：ED =2：3，求 n 的值；（3）如图 2，点 F 为抛物线上第一象限一点，且 AF 交 y 轴于点 G，连接 FB 并延长交 y 轴于点 H，且AGH =ABH，试说明无论 n 为何值，点 F 总在某
8、定直线上运动并直接写出当 AFB=45时，点 F 的坐标第 6 页，共 21 页答案和解析1.【答案】C【解析】解：根据相反数的含义，可得 2 的相反数是：-2 故选：C 根据相反数的含义，可得求一个数的相反数的方法就是在这个数的前边添加“-”，据此解答即可此题主要考查了相反数的含义以及求法，要熟练掌握，解答此题的关键是要明确：相反数是成对出现的，不能单独存在；求一个数的相反数的方法就是在这个数的前边添加“-”2.【答案】D【解析】解：（x-3） 0 有意义， x-30， x3， 故选：D根据 0 指数幂有意义的条件解答本题考查了 0 指数幂有意义的条件，要知道，底数不为 03.【答案】B【解
9、析】解：将这组数据重新排列为 1、1、2、2、3、3，所以这组数据的中位数为 =2，故选：B 根据中位数的定义求解即可本题考查了中位数的知识，属于基础题，解答本 题的关键是熟练掌握中位数的定义4.【答案】A【解析】第 7 页，共 21 页解：点 A（2，1）与点 A（2，-1），横坐 标相同，纵坐标不同， 点 A（2，1）与点 A（2，-1）关于 x 轴对称 故选：A直接利用关于 x 轴对称点的性质得出答案此题主要考查了关于 x 轴对称点的性质，正确记忆横纵坐标的关系是解题关键5.【答案】A【解析】解：综合三视图可以得出，这个几何体的底层应该有 4 个，第二层第二列第二排有 2 个，因此这个几
10、何体只能是 A 故选：A根据主视图、左视图、俯视图是分别从物体正面、左面和上面看所得到的 图形，即可得出答案本题考查了由三视图判断几何体，掌握口诀“俯视图 打地基，正视图疯狂盖，左视图拆违章” 是本题的关 键6.【答案】A【解析】解：画树状图如下：由树状图知，共有 4 种等可能结果，其中第二次 传球后球回到甲手中的有 2种结果，所以第二次传球后球回到甲手中的概率为 = ，故选：A首先根据题意画出树状图，然后由树状图求得所有等可能的结果与经过 2 次第 8 页，共 21 页传球后，球仍回到甲手中的情况，再利用概率公式求解即可求得答案本题考查的是用列表法或画树状图法求概率列表法或画树状图法可以不重
11、复不遗漏的列出所有可能的结果，列表法适合于两步完成的事件，树状图法适合两步或两步以上完成的事件注意概率=所求情况数与总情况数之比7.【答案】D【解析】解： ，2+得：7x=21 ，即 x=3，将 x=3 代入得：y=-2，P（3，-2），则 P 在第四象限故选：D求出方程组的解得到 x 与 y 的值，即可做出判断此题考查了解二元一次方程组，以及点的坐标，熟 练掌握运算法则是解本题的关键8.【答案】B【解析】解：由图表可得：第一行为 21+20； 第二行为：2 2+20，22+21， 第三行为：2 3+20，23+21，23+22， 34=25+21，65=26+20，96=26+25， 故选：
12、B 观察图表可知：第一行为 21+20；第二行为：2 2+20，22+21，进而根据规律解答即可本题考查规律型-数字问题，解题的关键是学会观察，探究规律，利用 规律解决问题9.【答案】C【解析】第 9 页，共 21 页解：由图象可知：将此抛物线在 x 轴下方的部分沿 x 轴往上翻折，得到一个新的函数图象的顶点的纵坐标为 5，|ax2+bx+c|=m 的图象是 x 轴上方部分（包含与 x 轴 的两个交点），（1）当 m=0 时 ，|ax2+bx+c|=m 有两个不相等的实数根，（2）在 x 轴上方时，只有 m5 时，作平行于 x 轴的直线才会与图象有两个交点，m=0 或 m5故选：C 利用图象法
13、：首先得出新的函数图象的顶点坐标，再结合图象即可得出 m 的取值范围考查了抛物线与 x 轴的交点，解题的关键是利用图象法解决问题，体现了转化的思想，把求方程的根，转化为函数图象的交点问题10.【答案】A【解析】解：延长 AD、BC 交于点 E，四边形 ABCD 内接于O，ECD=A=90，EDC=B，cosB= ，cosEDC= = ，即 = ，解得，DE= ，由勾股定理得，EC= = ，ECD=A，E=E，ECDEAB，第 10 页，共 21 页 = ，即 = ，解得，AD=6，故选：A延长 AD、BC 交于点 E，根据余弦的定义求出 DE，根据相似三角形的性质求出 AD本题考查的是圆内接四
14、边形的性质、相似三角形的判定和性质、勾股定理，掌握圆内接四边形的性质定理是解题的关键11.【答案】2【解析】解：原式= = = =2故答案为：2先化成最简根式再根据二次根式的除法法则相除即可求解此题主要考查的是二次根式的除法，比较简单，熟 记除法法则即可计算12.【答案】0.7【解析】解：观察可得：至少有一个球是白球的概率是：0.7； 故答案为：0.7观察表格，即可求得答案本题考查用样本估计总体，解题的关键是观察表格得出答案13.【答案】21【解析】解：原式= += ，故答案为： 根据分式的运算法则即可求出答案第 11 页，共 21 页本题考查分式的运算，解题的关键是熟练运用分式的运算法则，本
15、题属于基础题型14.【答案】 c941【解析】解：因为 c 是 钝角三角形的最大 边，所以 c 4+5 ，即 c 9故答案为： c 9三角形两边之和大于第三边根据三角形的三边关系以及勾股定理就可以求得第三边 c 的范 围本题考查了三角形三边关系和非负数的性质，根据三角形三边关系定理结合题目的已知条件列出不等式，然后解不等式即可15.【答案】4【解析】解：设 P 点坐 标为（a， ），则 PB= =a+ -2，PA= =a+ +2，所以 PA-PB=4故答案为 4设 P 点坐标为 （a， ），用 a 表示出 PA 和 PB 的表达式即可求二者之差本题主要考查反比例函数图象上点的坐标特征16.【答
16、案】2.8【解析】解：作 EHBD 于 H，由折叠的性质可知，EG=EA，由题意得，BD=DG+BG=8，四边形 ABCD 是菱形，AD=AB，ABD=CBD= ABC=60，第 12 页，共 21 页ABD 为等 边三角形，AB=BD=8，设 BE=x，则 EG=AE=8-x，在 RtEHB 中，BH= x，EH= x，在 RtEHG 中，EG 2=EH2+GH2，即（8-x） 2=（ x）2+（6- x）2，解得，x=2.8，即 BE=2.8，故答案为：2.8作 EHBD 于 H，根据折叠的性质得到 EG=EA，根据菱形的性质、等边三角形的判定定理得到ABD 为等边三角形，得到 AB=BD
17、，根据勾股定理列出方程，解方程即可本题考查的是翻转变换的性质、菱形的性质、勾股定理、解直角三角形，掌握翻转变换是一种对称变换，折叠前后图形的形状和大小不变，位置变化， 对应边和对应角相等是解题的关键17.【答案】解：原式=4a 4+8a4-9a4 =3a4【解析】先计算除法、乘法和乘方，再合并同类项即可得本题主要考查整式的混合运算，解题的关键是掌握整式的混合运算顺序和运算法则18.【答案】解：如图，ABCD，1=CDE，CE=CD，E=CDE，E=1，ABC=E+1=21，AB=BF，BAF=F= （180- ABF），12设1=2=，则ABF=2 ，BAF=F=90-，EOF=2+BAF=+
18、90-=90，EOF 的度数为 90【解析】第 13 页，共 21 页根据平行线的性质得到1=CDE，根据等腰三角形的性质得到E=CDE，由三角形外角的性质得到ABC= E+1=21，求得 BAF=F= （180-ABF），设1=2=，则ABF=2，于是得到结论本题考查了等腰三角形的性质，平行线的性质，三角形的外角的性质，正确的识别图形是解题的关键19.【答案】50 72【解析】解：（1）抽取学生的人数为 1326%=50（人），故答案为：50；（2）C 级 学生所在的扇形圆心角的度数为 360 =72，故答案为：72 ；（3）估计这次考试中 A 级和 B 级的学生共有 500（26%+50%
19、）=380（人）（1）用 A 等级人数除以其对应百分比可得总人数；（2）用 360乘以 C 等级人数占被 调查人数的比例即可得；（3）用总人数乘以样本中 A 和 B 的百分比之和本题考查了扇形图和条形图的相关知识题目难度不大扇形图中某项的百分比=该项 人数 总人数100%，扇形 图中某项圆心角的度数=360 该项在扇形图中的百分比20.【答案】6+ （2，4）132【解析】第 14 页，共 21 页解：（1）如图，A 1B1C1 和A 2B2C2 为所作；（2）点 C 的运动路径长=6+ =6+ ；（3）点 P 的坐 标为（2， 4）故答案为 6+ ；（2，4）（1）利用点平移的坐标规律写出
20、A1、B1、C1 的坐标，然后描点得到 A1B1C1，再利用网格特点和旋转的性质画出 A2、B2、C2 得到A 2B2C2；（2）点 C 的运动路径长为平移的距离和弧 C1C2 的长；（3）作 AA2 和 CC2 的垂直平分线，它 们的交点为 P 点本题考查了作图-旋转变换：根据旋转的性质可知，对应角都相等都等于旋转角，对应线段也相等，由此可以通过作相等的角，在角的边上截取相等的线段的方法，找到对应点，顺次连接得出旋转后的图形也考查了对称轴变换21.【答案】（1）证明：如图，连接 OD，AD 为BAC 的角平分线，BAD=CAD，OA=OD，ODA=OAD，ODA=CAD，ODAC，C=90，
21、ODC=90，ODBC，BC 为圆 O 的切线；（2）连接 EF，在 RtBOD 中，sinB= ，=513设圆的半径为 r，可得 ，+8=513解得：r=5， AE=10，AB=18，第 15 页，共 21 页AE 是直径，AFE=C=90，EFBC，AEF=B，sinAEF= ，=513AF=AEsinAEF=10 = ，5135013AFOD， ，即 DG= AD，=50135=1013 1323ABDADF=AD2=ABAF=18 ，5013AD= ，301313DG= 1323301313=301323【解析】（1）连接 OD，由 AD 为角平分线得到一对角相等，再由等边对等角得到一
22、对角相等，等量代换得到内错角相等， 进而得到 OD 与 AC 平行，得到 OD 与BC 垂直，即可得 证； （2）连接 EF，设圆的半径为 r，由 sinB 的值，利用锐 角三角函数定义求出 r 的值，由直径所对的圆周角为直角，得到 EF 与 BC 平行，得到 sinAEF=sinB，进而求出 DG 的长即可本题考查了切线的判定与圆周角定理以及直角三角形边角关系，熟练掌握圆的相关知识是解题的关键22.【答案】解：（1）设 y=kx+b，直线 y=kx+b 经过点（40，300），（55，150）， ，40+=30055+=150解得： =10=700故 y 与 x 之间的函数关系式为：y =-
23、10x+700，（2）由题意，得-10x+700240，解得 x46，第 16 页，共 21 页30x 46，设利润为 w=（x -30）y =（x-30）（-10x+700），w=-10x2+1000x-21000=-10（x-50） 2+4000，-100，x50 时，w 随 x 的增大而增大，x=46 时， w 最大 =-10（46-50） 2+4000=3840，答：当销售单价为 46 元时，每天获取的利润最大，最大利润是 3840 元；（3）w-150=-10x 2+1000x-21000-150=3600，-10（x-50） 2=-250，x-50=5，x1=55，x 2=45，如
24、图所示，由图象得：当 45x55 时，捐款后每天剩余利润不低于 3600 元【解析】（1）可用待定系数法来确定 y 与 x 之间的函数关系式； （2）根据利润=销售量 单件的利 润，然后将（1）中的函数式代入其中，求出利润和销售单件之间的关系式，然后根据其性质来判断出最大利润； （3）首先得出 w 与 x 的函数关系式， 进而利用所获利润等于 3600 元时，对应x 的值，根据增减性，求出 x 的取值范围此题主要考查了二次函数的应用、一次函数的应用和一元二次方程的应用，利用函数增减性得出最值是解题关键，能从实际问题中抽象出二次函数模型是解答本题的重点和难点23.【答案】 5【解析】（1）证明：
25、AHCG，EGCG，ADCE，AHD=G=AFC=90，A+ADC=C+CDF=90，A=C，第 17 页，共 21 页ADHCEG， ；（2）解：如图 2，过点 A 作 AMBC 于点 M，过点 E 作 EHBC 于点 H，tanB=m=2= = ，设 EH=2x，BH=x，AM=2BMBE= = x，AFEC，AMCDADC+DCE=90，ADC+DAM=90，DAM=DCE，且 AMD=EHC=90EHCDMA，且 AD=2EC， = = =2，DM=2EH=4x，AM=2HC，AM=2HC，AM=2BMHC=BMHC-HM=BM-HMBH=MC=xDC=DM+MC=5x = = ，故答
26、案为： ；（3）解：如图 3，作 BCF=B，交 AB 于点 F，过点 D 作 GDBD 交 BA 的延长线于点 G，过点 F 作 FHBC 于点 H，tanB=m= ，B=30，BCF=B=30，BF=FC，且 FHBC，BC=4 ，BH=HC=2 ，且B=30 ，FHBCFH=2，BF=FC=4，CD=3 ，BC=4 ，BD=7 ，又BCF= B=30，GDBD，G=60，AFC=60，GD=7，BG=2DG=14，BCA=BDE+CMD=BDE+60=BCF+ACF=30+ACF，ACF=30+BDE，且AEM= B+BDE=30+BDE，ACF=AEM，且 G=AFC=60第 18 页
27、，共 21 页GEDFCA = = ，且 DE=2AC，GD=2AF，EG=2FC=8，AF= ，BE=BG-EG=14-8=6（1）根据余角的性质和相似三角形的判定和性质定理即可得到结论；（2）过点 A 作 AMBC 于点 M，过点 E 作 EHBC 于点 H，设EH=2x，BH=x，由勾股定理可得 BE= x，可证EHC DMA，可得 = ，可得 DM=2EH=4x，AM=2HC，可求 DC=DM+MC=5x，即可求= ；（3）作BCF=B，交 AB 于点 F，过点 D 作 GDBD 交 BA 的延长线于点 G，过点 F 作 FHBC 于点 H，由直角三角形的性 质可求FH=2，BF=FC
28、=4，GD=7，BG=2DG=14，可证GEDFCA，可得 = =，即可求 GD=2AF，EG=2FC=8，由三角形面积公式可求 BED 的面积本题是相似三角形综合题，考查了相似三角形的判定，勾股定理，直角三角形的性质，锐角三角函数等知识，添加恰当 辅助线构造相似三角形是本题的关键24.【答案】解：（1）当 n=0 时，抛物线解析式为 y= x2-2，12令 x=0，y=-2，C（0，-2），令 y=0，x 1=-2，x 2=2，A（ -2，0），B（2，0）（2）如图所示，过点 D 作 y 轴的垂线，垂足为 F，第 19 页，共 21 页令 x=0，y=-4n-2 ，C（0，-4 n-2），
29、OC=4 n+2，令 y=0，x 1=2，x 2=-4n-2，B（ 2，0），A（-4n-2，0），OB=2，OA =4n+2，BCAD， ，即 ，= 24+2=4+2OE= （4n+2） 2，12DFOA， ，即= 4+2= 12(4+2)2 ，=32DF= =6n+3，FE= （4n+2） 2，32(4+2) 34D（ 6n+3， （4n+2） 2），代入抛物线得，54（4n+2） 2= （6n+3） 2+2n（6n+3）-4n-2 ，54 12解得 n1= ，n 2=- （舍）12 12n= 12（3）如图所示，过点 F 作 y 轴的垂线，垂足为 Q，过点 F 作 x 轴的垂线，垂足为
30、E，第 20 页，共 21 页设点 F 的坐标为（m， m2+2mn-4n-2），12EB=m-2，EF= m2+2mn-4n-2，12OHEF， ，即 ，= 122+242 =22OH=4n+2+m，AE=4n+2+m，OH=AE，AGH=ABH，AFB=ABH，AEF=BOH，AFEOBH（AAS），EF=OB=2，F（ m，2），点 F 一定在定直线 y=2 上运动，当AFB=45 时，过点 B 作 BP 垂直于 FB，过点 P 作 x 轴的垂线，垂足为点 D，FBEBPD（AAS ），BD=EF=2，OB=2，D 与 O 重合，P 与 G 重合，OG=BE=m-2，QG=2-（m-2）
31、=4-m，FQGFBE， ，即 ，= 2=24解得 m1=2 ，m 2=-2 （舍），2 2F（ 2 ，2）2【解析】（1）当 n=0 时 ，抛物线的解析式已知，令 x=0，可求出点 C 的坐标，令 y=0，可求出点 A、B 的坐标 第 21 页，共 21 页（2）令 x=0，求得点 C 的坐标，令 y=0，求出点 A、B 的坐标，根据三角形的相似可求出 OE 的长度，表示点 D 的坐标，代入抛物线中，即可求出 n 的值 （3）设点 F 的坐 标，利用 AGH=ABH，可以得到 这两个的三角函数相等，从而找到隐藏的线段相等，得到三角形全等，从而得出点 F 的纵坐标为定值 2，再根据 45角构造等腰直角三角形，构造三角形全等，找到等量关系列式求解此题考查了几何图形与二次函数的结合，找到题里隐藏的全等三角形是解题关键，还考查了相似三角形的性质及其判定， 综合性较强
