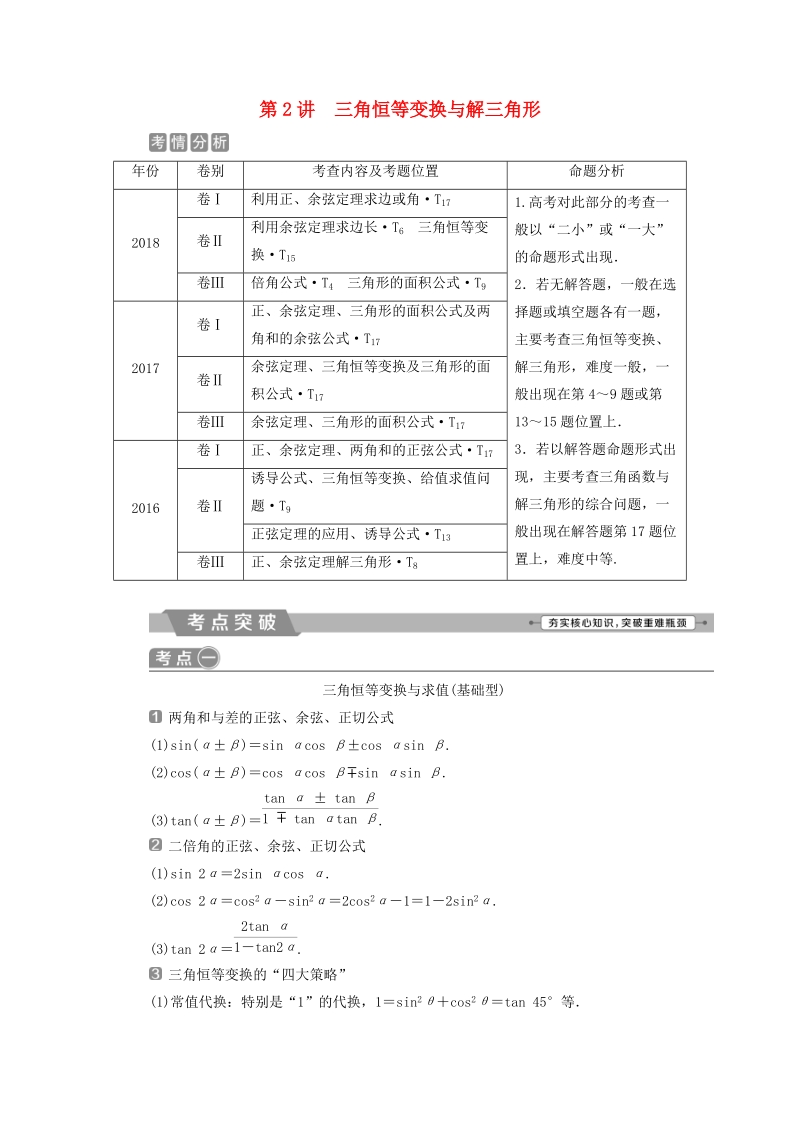
1、第 2 讲 三角恒等变换与解三角形年份 卷别 考查内容及考题位置 命题分析卷 利用正、余弦定理求边或角T 17卷利用余弦定理求边长T 6 三角恒等变换T 152018卷 倍角公式T 4 三角形的面积公式T 9卷正、余弦定理、三角形的面积公式及两角和的余弦公式T 17卷余弦定理、三角恒等变换及三角形的面积公式T 172017卷 余弦定理、三角形的面积公式T 17卷 正、余弦定理、两角和的正弦公式T 17诱导公式、三角恒等变换、给值求值问题T 9卷正弦定理的应用、诱导公式T 132016卷 正、余弦定理解三角形T 81.高考对此部分的考查一般以“二小”或“一大”的命题形式出现2若无解答题，一般在选
2、择题或填空题各有一题，主要考查三角恒等变换、解三角形，难度一般，一般出现在第 49 题或第1315 题位置上3若以解答题命题形式出现，主要考查三角函数与解三角形的综合问题，一般出现在解答题第 17 题位置上，难度中等.三角恒等变换与求值(基础型)两角和与差的正弦、余弦、正切公式(1)sin( )sin cos cos sin .(2)cos( )cos cos sin sin .(3)tan( ) .tan tan 1tan tan 二倍角的正弦、余弦、正切公式(1)sin 2 2sin cos .(2)cos 2 cos 2 sin 2 2cos 2 112sin 2 .(3)tan 2 .
3、2tan 1 tan2三角恒等变换的“四大策略”(1)常值代换：特别是“1”的代换，1sin 2 cos 2 tan 45等(2)项的分拆与角的配凑：如 sin2 2cos 2 (sin 2 cos 2 )cos 2 ， ( ) 等(3)降次与升次：正用二倍角公式升次，逆用二倍角公式降次(4)弦、切互化：一般是切化弦考法全练1已知 ，tan 2，则 cos _(0， 2) ( 4)解析：因为 ，tan 2，(0， 2)所以 sin ，cos ，255 55所以 cos cos cos sin sin( 4) 4 4 .22 (255 55) 31010答案：310102已知 cos ，cos(
4、 ) ，且 ， ，则 cos( )13 13 (0， 2)_解析：因为 ，所以 2 (0，)(0， 2)因为 cos ，所以 cos 2 2cos 2 1 ，13 79所以 sin 2 ，1 cos22429又 ， ，(0， 2)所以 (0，)，所以 sin( ) ，1 cos2（ ）223所以 cos( )cos2 ( )cos 2 cos( )sin 2 sin( ) .(79) ( 13) 429 223 2327答案：23273已知 sin ，且 sin( )cos ，则 tan( )35( 20，所以 sin B2sin Bcos C，所以 cos C .12因为 C(0，)，所以
5、C . 3(2)由(1)及余弦定理得 cos C ，a2 b2 c22ab 12又 c2 ，所以 a2 b212 ab，3所以( a b)2123 ab3 ，(a b2 )2 即( a b)248(当且仅当 a b2 时等号成立)3所以 a b4 ， a b c6 .3 3所以 ABC 周长的最大值为 6 .32(2018武汉调研)在锐角 ABC 中，内角 A， B， C 的对边分别是 a， b， c，满足cos 2Acos 2 B2cos cos 0.( 6 B) ( 6 B)(1)求角 A 的值；(2)若 b 且 b a，求 a 的取值范围3解：(1)由 cos 2Acos 2B2cos
6、cos 0，得 2sin2B2sin 2A2( 6 B) ( 6 B)0，化简得 sin A ，又 ABC 为锐角三角形，故 A .(34cos2B 14sin2B) 32 3(2)因为 b a，所以 c a，所以 C ， B ，所以 sin B .3 3 2 6 3 12 32由正弦定理 ，得 ，所以 a ，asin A bsin B a32 3sin B 32sin B由 sin B 得 a ，3)(12， 32 3A 组 夯基保分专练一、选择题1(2018高考全国卷)已知函数 f(x)2cos 2xsin 2x2，则( )A f(x)的最小正周期为 ，最大值为 3B f(x)的最小正周期
7、为 ，最大值为 4C f(x)的最小正周期为 2，最大值为 3D f(x)的最小正周期为 2，最大值为 4解析：选 B.易知 f(x)2cos 2xsin 2x23cos 2x1 (2cos2x1) 1 cos 32 32 322x ，则 f(x)的最小正周期为 ，当 x k( kZ)时， f(x)取得最大值，最大值为 4.522在 ABC 中，内角 A， B， C 的对边分别是 a， b， c，若 c2 a， bsin B asin A asin C，则 sin B 为( )12A. B.74 34C. D.73 13解析：选 A.由 bsin B asin A asin C，12且 c2
8、a，得 b a，2因为 cos B ，a2 c2 b22ac a2 4a2 2a24a2 34所以 sin B .1 (34)2 743(2018洛阳第一次统考)在 ABC 中，角 A， B， C 的对边分别是 a， b， c，若a， b， c 成等比数列，且 a2 c2 ac bc，则 ( )cbsin BA. B.32 233C. D.33 3解析：选 B.由 a， b， c 成等比数列得 b2 ac，则有 a2 c2 b2 bc，由余弦定理得cos A ，故 A ，对于 b2 ac，由正弦定理得，sin 2 Bsin Asin b2 c2 a22bc bc2bc 12 3C sin C，
9、由正弦定理得， .故选 B.32 cbsin B sin Csin2 B sin C32sin C 2334(2018昆明模拟)在 ABC 中，已知 AB ， AC ，tan BAC3，则 BC 边上2 5的高等于( )A1 B. 2C. D23解析：选 A.法一：因为 tan BAC3，所以 sin BAC ，cos BAC .由310 110余弦定理，得 BC2 AC2 AB22 ACABcos BAC522 9，所以5 2 ( 110)BC3，所以 S ABC ABACsin BAC ，所以 BC 边上的高 h12 12 2 5 310 32 1，故选 A.2S ABCBC 2323法二
10、：因为 tan BAC3，所以 cos BAC 0，则 BAC 为钝角，因此 BC 边110上的高小于 ，故选 A.25 ABC 的内角 A， B， C 的对边分别为 a， b， c.已知 sin Bsin A(sin Ccos C)0， a2， c ，则 C( )2A. B.12 6C. D. 4 3解析：选 B.因为 sin Bsin A(sin Ccos C)0，所以 sin(A C)sin Asin Csin Acos C0，所以 sin Acos Ccos Asin Csin Asin Csin Acos C0，整理得sin C(sin Acos A)0.因为 sin C0，所以 s
11、in Acos A0，所以 tan A1，因为 A(0，)，所以 A .34由正弦定理得 sin C ，csin Aa 2222 12又 0C ，所以 C . 4 66.如图，在 ABC 中， C ， BC4，点 D 在边 AC 上， 3AD DB， DE AB， E 为垂足若 DE2 ，则 cos A 等于( )2A. B.223 24C. D.64 63解析：选 C.依题意得， BD AD ， BDC ABD A2 A.在 BCDDEsin A 22sin A中， ， ，即 ，由此BCsin BDC BDsin C 4sin 2A 22sin A 23 423sin A 42sin Aco
12、s A 423sin A解得 cos A .64二、填空题7若 sin ，则 cos _( 3 ) 14 ( 3 2 )解析：依题意得 cos( 3 2 )cos ( 3 2 )cos 2( 3 )2sin 2 12 1( 3 ) (14)2 .78答案：788(2018高考全国卷改编)在 ABC 中，cos ， BC1， AC5，则C2 55AB_解析：因为 cos C2cos 2 12 1 ，所以由余弦定理，得C2 15 35AB2 AC2 BC22 ACBCcos C251251 32，所以 AB4 .(35) 2答案：4 29(2018惠州第一次调研)已知 a， b， c 是 ABC
13、中角 A， B， C 的对边，a4， b(4，6)，sin 2 Asin C，则 c 的取值范围为_解析：由 ，得 ，所以 c8cos A，因为4sin A csin C 4sin A csin 2A16 b2 c22 bccos A，所以 16 b264cos 2A16 bcos2A，又 b4，所以cos2A ，所以 c264cos 2A64 164 b.因为16 b264 16b （ 4 b） （ 4 b）16（ 4 b） 4 b16 4 b16b(4，6)，所以 32c240，所以 4 c2 .2 10答案：(4 ，2 )2 10三、解答题10(2018沈阳教学质量监测(一)在 ABC
14、中，已知内角 A， B， C 的对边分别是a， b， c，且 2ccos B2 a b.(1)求 C；(2)若 a b6， ABC 的面积为 2 ，求 c.3解：(1)由正弦定理得 2sin Ccos B2sin Asin B，又 sin Asin( B C)，所以 2sin Ccos B2sin( B C)sin B，所以 2sin Ccos B2sin Bcos C2cos Bsin Csin B，所以 2sin Bcos Csin B0，因为 sin B0，所以 cos C .12又 C(0，)，所以 C .23(2)因为 S ABC absin C2 ，12 3所以 ab8，由余弦定理
15、，得 c2 a2 b22 abcos C a2 ab b2( a b)2 ab28，所以 c2 .711(2018石家庄质量检测(二)已知 ABC 的内角 A、 B、 C 的对边分别为 a、 b、 c，且 tan Atan B.3cacos B(1)求角 A 的大小；(2)设 AD 为 BC 边上的高， a ，求 AD 的取值范围3解：(1)在 ABC 中，因为 tan Atan B，所以 ，3cacos B 3sin Csin Acos B sin Acos A sin Bcos B即 ，3sin Csin Acos B sin Acos B sin Bcos Acos Acos B所以 ，
16、则 tan A ，所以 A .3sin A 1cos A 3 3(2)因为 S ABC ADBC bcsin A，12 12所以 AD bc.12由余弦定理得 cos A ，12 b2 c2 a22bc 2bc 32bc所以 0bc3(当且仅当 b c 时等号成立)，所以 0AD .3212(2018郑州质量检测(二)已知 ABC 内接于半径为 R 的圆， a， b， c 分别是角A， B， C 的对边，且 2R(sin2Bsin 2A)( b c)sin C， c3.(1)求 A；(2)若 AD 是 BC 边上的中线， AD ，求 ABC 的面积192解：(1)对于 2R(sin2Bsin
17、2A)( b c)sin C，由正弦定理得，bsin B asin A bsin C csin C，即 b2 a2 bc c2，所以 cos A ，因为 0A180，所以 A60.b2 c2 a22bc 12(2)以 AB， AC 为邻边作平行四边形 ABEC，连接 DE，易知 A， D， E 三点共线在 ABE 中， ABE120， AE2 AD ，19在 ABE 中，由余弦定理得 AE2 AB2 BE22 ABBEcos 120，即 199 AC223 AC ，得 AC2.(12)故 S ABC bcsin BAC .12 332B 组 大题增分专练1(2018长春质量监测(二)在 ABC
18、 中，内角 A， B， C 的对边分别为 a， b， c，其面积 S b2sin A.(1)求 的值；cb(2)设内角 A 的平分线 AD 交于 BC 于 D， AD ， a ，求 b.233 3解：(1)由 S bcsin A b2sin A，可知 c2 b，即 2.12 cb(2)由角平分线定理可知， BD ， CD ，233 33在 ABC 中，cos B ，在 ABD 中，cos B ，即 4b2 3 b222b34b2 43 4322b233 4b2 3 b222b3，解得 b1.4b2 43 4322b2332(2018贵阳模拟)已知在 ABC 中，角 A， B， C 所对的边长分
19、别为 a， b， c， AB 边上的高 h c.23(1)若 ABC 为锐角三角形，且 cos A ，求角 C 的正弦值；35(2)若 C ， M ，求 M 的值 4 a2 b2 13c2ab解：(1)作 CD AB，垂足为 D，因为 ABC 为锐角三角形，且 cos A ，35所以 sin A ，tan A ，45 43所以 AD ， BD AB AD ，c2 c2所以 BC ，CD2 BD2 (23c)2 (c2)2 5c6由正弦定理得：sin ACB .ABsin ABCc455c6 2425(2)因为 S ABC c c absin ACB ab，12 23 12 24所以 c2 ab
20、，324又 a2 b2 c22 abcos ACB ab，2所以 a2 b2 ab c2，2所以 a2 b2 c2 ab c2 ab ab2 ab，13 2 43 2 43 324 2所以 M 2 .a2 b2 13c2ab 22abab 23(2018合肥质量检测)已知 ABC 中， D 为 AC 边上一点， BC2 ， DBC45.2(1)若 CD2 ，求 BCD 的面积；5(2)若角 C 为锐角， AB6 ，sin A ，求 CD 的长21010解：(1)在 BCD 中， CD2 BC2 BD22 BCBDcos 45，即 208 BD24 BD，解得 BD6，所以 BCD 的面积 S
21、2 6sin 456.12 2(2)在 ABC 中，由 得 ，BCsin A ABsin C 221010 62sin C解得 sin C .31010由角 C 为锐角得，cos C ，1010所以 sin BDCsin( C45) .255在 BCD 中， ，即 ，CDsin DBC BCsin BDC CD22 22255解得 CD .54(2018高考天津卷)在 ABC 中，内角 A， B， C 所对的边分别为 a， b， c.已知bsin A acos .(B 6)(1)求角 B 的大小；(2)设 a2， c3，求 b 和 sin(2A B)的值解：(1)在 ABC 中，由正弦定理 ，
22、可得 bsin A asin B，又由 bsin asin A bsin BA acos ，得 asin B acos ，即 sin Bcos ，可得 tan B .又(B 6) (B 6) (B 6) 3因为 B(0，)，可得 B . 3(2)在 ABC 中，由余弦定理及 a2， c3， B ，有 b2 a2 c22 accos B7，故 3b .7由 bsin A acos ，(B 6)可得 sin A .37因为 ac，故 cos A .27因此 sin 2A2sin Acos A ，437cos 2A2cos 2A1 ，17所以，sin(2 A B)sin 2 Acos Bcos 2 Asin B .437 12 17 32 3314
