1、绝 密 启 用 前2018 年 普 通 高 等 学 校 招 生 全 国 统 一 考 试 仿 真 卷理科数学（七）本 试 题 卷 共 14 页 ， 23 题 （ 含 选 考 题 ） 。 全 卷 满 分 150 分 。 考 试 用 时 120 分 钟 。祝 考 试 顺 利 注 意 事 项 ：1、 答 题 前 ， 先 将 自 己 的 姓 名 、 准 考 证 号 填 写 在 试 题 卷 和 答 题 卡 上 ， 并 将 准 考 证 号 条 形 码 粘 贴在 答 题 卡 上 的 指 定 位 置 。 用 2B 铅 笔 将 答 题 卡 上 试 卷 类 型 A 后 的 方 框 涂 黑 。2、 选 择 题 的 作
2、 答 ： 每 小 题 选 出 答 案 后 ， 用 2B 铅 笔 把 答 题 卡 上 对 应 题 目 的 答 案 标 号 涂 黑 。 写在 试 题 卷 、 草 稿 纸 和 答 题 卡 上 的 非 答 题 区 域 均 无 效 。3、 填 空 题 和 解 答 题 的 作 答 ： 用 签 字 笔 直 接 答 在 答 题 卡 上 对 应 的 答 题 区 域 内 。 写 在 试 题 卷 、 草稿 纸 和 答 题 卡 上 的 非 答 题 区 域 均 无 效 。4、 选 考 题 的 作 答 ： 先 把 所 选 题 目 的 题 号 在 答 题 卡 上 指 定 的 位 置 用 2B 铅 笔 涂 黑 。 答 案 写
3、 在答 题 卡 上 对 应 的 答 题 区 域 内 ， 写 在 试 题 卷 、 草 稿 纸 和 答 题 卡 上 的 非 答 题 区 域 均 无 效 。5、 考 试 结 束 后 ， 请 将 本 试 题 卷 和 答 题 卡 一 并 上 交 。第 卷一 、 选 择 题 ： 本 大 题 共 12 小 题 ， 每 小 题 5 分 ， 在 每 小 题 给 出 的 四 个 选 项 中 ， 只 有一 项 是 符 合 题 目 要 求 的 。12018孝义模拟 已知全集 ，若 ， ，则 等,34U1,3ABUAB于（ ）A B C D,21,42, 2,4【答案】D【解析】根据题意得到 ， ，故得到 故答 2,U
4、AUB1,4UAB,案为：D22018海南二模 已知复数 满足 ， 为 的共轭复数，则 （ z3iizz）A B C D12 4【答案】A【解析】由题意得：， ，34iii 724ii9165z724i5z，故选：A227532018大同一中 如果数据 ， ， 的平均数为 ，方差为 ，则 ，1x2nxx2815x， 的平均数和方差分别为（ ）2x2nxA B C D,825,825,8x2,x【答案】C【解析】根据平均数的概念，其平均数为 ，方差为 ，故选 C2542018龙岩期末 九章算术有这样一个问题：今有女子善织，日增等尺，七日共织二十八尺，第二日、第五日、第八日所织之和为十五尺，则第十
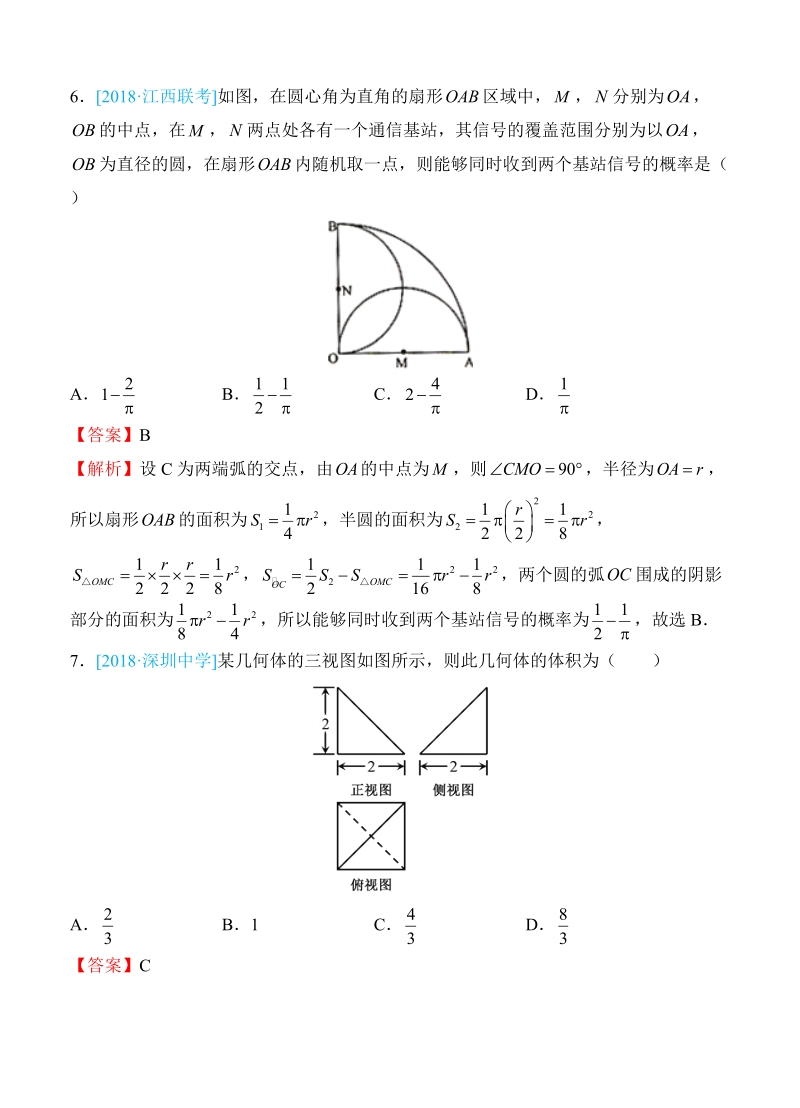
5、日所织尺数为（ ）A9 B10 C11 D12【答案】B【解析】设第一天织布 尺，从第二天起每天比第一天多织 尺，由已知得：1ad，解得 ， ，第十日所织尺数为111728475ad1ad，故选 B09052018宁德质检 已知 ， ， ，则（ ）0.49a0.4log19b1.9cA B C Dabccabcab【答案】C【解析】 ， ， ，0.41910.40.4log91lb1.904，故选 Cacb62018江西联考 如图，在圆心角为直角的扇形 区域中， ， 分别为 ，OABMNOA的中点，在 ， 两点处各有一个通信基站，其信号的覆盖范围分别为以 ，OBMN为直径的圆，在扇形 内随机取
6、一点，则能够同时收到两个基站信号的概率是（ OAB）A B C D2112421【答案】B【解析】设 C 为两端弧的交点，由 的中点为 ，则 ，半径为 ，OAM90COAr所以扇形 的面积为 ，半圆的面积为 ，OA214Sr22218rS， ，两个圆的弧 围成的阴影2128MCrS A26OMCOCSr部分的面积为 ，所以能够同时收到两个基站信号的概率为 ，故选 B4r 1272018深圳中学 某几何体的三视图如图所示，则此几何体的体积为（ ）A B1 C D23 4383【答案】C【解析】该几何体为三棱锥，其直观图如图所示，体积 14233V故选 C82018海南二模 已知函数 ，则关于 的
7、2017logxf20173xxx不等式 的解集为（ ）126fxfA B C D,1,4【答案】A【解析】由题意易知： 为奇函数且在2017207logxxgx上单调递增， ，即 ， 136 21gx ， ，21xx不等式 的解集为 ，故选：A 6ff,192018宿州一模 在如图所示的程序框图中，若输入的 ，输出的 ，则判2s2018s断框内可以填入的条件是（ ） 开 始输 入 x结 束是否 输 出 s2s1i1iA B C D9i10i 10i 1i【答案】D【解析】输入 ， ， ； ， ；当 ， ；2Si24Si382S0i12048S当 ，当 时，满足条件，退出循环， ，故选 D10
8、i1 4102018华师附中 已知关于 的方程 在区间 上有两xsinsi2xxm,个根 ，且 ，则实数 的取值范围是（ ）12,x12x mA B C D55,11,50,1【答案】D【解析】 ，即 ，所以 ，sinsi2xxmsincoxm2sin4xm，作出函数 ， 的图像，由图可知，要使得方i4xi4y0,程在区间 上有两个根 ， ，且 ，则 ，0,21,x212x 2m即 故选 D1m112018阳春一中 已知 是函数 的导函数，且对任意的实数 都有fxfxx（ 是自然对数的底数） ， ，若不等式 的解e23xfe01f0fk集中恰有两个整数，则实数 的取值范围是（ ）kA B C
9、D21,0e21,0e2,e2,e【答案】C【解析】令 ，则 ，可设 ，exfG23exffG 23Gxc（ ）， ，01fc231xf可得： 时，函数 取得极大值，254e14exxfx 4fx时，函数 取得极小值 ， ， ， f0f1f210e，又当 时， 时，不等式 的310efxx2ek fxk解集中恰有两个整数 ， 故 的取值范围是 故答案选：C12k2,0122018佳木斯一中 已知椭圆 与抛物线 有相同的焦点 ， 为原点，215yx2xayFO点 是抛物线准线上一动点，点 在抛物线上，且 ，则 的最小值为PA4AFP（ ）A B C D21342316【答案】A【解析】 椭圆 ，
10、 ，即 ，则椭圆的焦点为 ，不妨215yx254c2c0,2取焦点 ， 抛物线 ， 抛物线的焦点坐标为 ， 椭圆0,2ay ,4a与抛物线 有相同的焦点 ， ，即 ，则抛物线方程为215yx2xF24a8，准线方程为 ， ，由抛物线的定义得： 到准线的距离为 ，28yAA4，即 点的纵坐标 ，又点 在抛物线上， ，不妨取点 坐标4yA24x， 关于准线的对称点的坐标为 ，则 ，即,24,6BPOBP， ， 三点共线时，有最小值，最小值为OPB，故选 A22461365213OB第 卷本 卷 包 括 必 考 题 和 选 考 题 两 部 分 。 第 (13)(21)题 为 必 考 题 ， 每 个
11、试 题 考 生 都必 须 作 答 。 第 (22)(23)题 为 选 考 题 ， 考 生 根 据 要 求 作 答 。二 、 填 空 题 ： 本 大 题 共 4 小 题 ， 每 小 题 5 分 。132018来宾调研 已知变量 满足约束条件 ，则 的最大,xy103xy 23zxy_【答案】4【解析】绘制不等式组表示的平面区域如图所示，结合目标函数的几何意义可知目标函数在点 处取得最大值，其最大值为： 1,2A max231324zy142018昆明一中 有甲、乙、丙、丁四位歌手参加比赛，其中只有一位获奖，有人走访了四位歌手，甲说：“ 我没有获奖 ”，乙说：“是丙获奖”，丙说：“ 是丁获奖”，丁
12、说：“我没有获奖 ”在以上问题中只有一人回答正确，根据以上的判断，获奖的歌手是_【答案】甲【解析】若甲回答正确，则正确表述为：甲：我未获奖；乙：丙未获奖；丙：丁未获奖；丁：我获奖此情况下丙、丁冲突，故错误；若乙回答正确，则正确表述为：甲：我获奖；乙：是丙获奖；丙：丁未获奖；丁：我获奖而只有一个人获奖，故错误；若丙回答正确，则正确表述为：甲：我获奖；乙：丙未获奖；丙：是丁获奖；丁：我获奖而只有一个人获奖，故错误；若丁回答正确，则正确表述为：甲：我获奖；乙：丙未获奖；丙：丁未获奖；丁：我没有获奖此时获奖人数只有一个，为甲故正确故答案为甲152018阳春一中 在面积为 2 的平行四边形 中，点 为直
13、线 上的动点，则ABCDPAD的最小值是_2PBC【答案】 23【解析】取 的中点 ，连接 ，因为平行四边形 ，面积为 ，所以BCQPABCD2， ， ，2PQ 2214BCPB，222221 334 4PCPBQBPQBC 此时 ，且 ，故答案为 Q32C162018黄山联考 已知 ， ， 是锐角 的内角 ， ， 所对的边，abcABC BC，且满足 ，则 的取值范围是_3b2cosBa【答案】 ,【解析】 ，2cosaAb由正弦定理可得 ，即 ，incosins0CBAsin2co10CB ， ， 为 的内角， ， ，sin0C1cos2B 3b根据正弦定理可知 ，2sinisinabcA
14、C ，2sii2ii3sin36acCC 是锐角三角形， ， 的取值范围为 ，故答案为AB 6ac,233,2三 、 解 答 题 ： 解 答 应 写 出 文 字 说 明 、 证 明 过 程 或 演 算 步 骤 。172018豫南九校 设正项等比数列 ， ，且 ， 的等差中项na4812a3为 123a（1）求数列 的通项公式；n（2）若 ，数列 的前 项和为 ，数列 满足 ， 为数321lognnbanbnSnc14nSnT列 的前 项和，求 ncnT【答案】 （1） ；（2） 3na21n【解析】 （1）设等比数列 的公比为 ，na0q由题意，得 ，3 分3412118 qa解得 ；5 分3
15、q所以 6 分1na（2）由（1）得 ，7 分213lognnb，9 分2nS ，10 分2114ncn 12 分13522n nTn 182018晋中调研 某省高中男生身高统计调查数据显示：全省 名男生的身高10服从正态分布 ，现从某校高三年级男生中随机抽取 名测量身高，测量发170.6N， 5现被测学生身高全部介于 和 之间，将测量结果按如下方式分成 组：5.cm187.5 6第一组 ，第二组 ，第六组 ，下图是按照上5.62.)， 26， 182.7.，述分组方法得到的频率分布直方图（1）求该学校高三年级男生的平均身高；（2）求这 名男生中身高在 以上（含 ）的人数；5017.5cm17
16、.5c（3）从这 名男生中身高在 以上（含 ）的人中任意抽取 人，该 中2身高排名（从高到低）在全省前 名的人数记为 ，求 的数学期望30（附：参考数据：若 服从正态分布 ，则 ，2N， ()0.68P， ）(2).954P (3)0.974P【答案】 （1） ；（2）10 人；（3） 7cm 1E【解析】 （1）由直方图可知该校高三年级男生平均身高为3 分60.501750.28.50.71.cm（2）由频率分布直方图知，后两组频率为 ，人数为 ，即这 名男生身250高在 以上（含 ）的人数为 人5 分17.c.c1（3） ，(0534170534).97P ，而 ，6 分.982 0130
17、所以全省前 名的身高在 以上（含 ） ，这 人中 以上（含182cm82.5c82.5cm）的有 人7 分.5cm随机变量 可取 ， ， ，8 分0于是 ， ， ，11251049Cp152049CP251049CP分 12 分229E192018天一大联考 棱台 的三视图与直观图如图所示1ABCD（1）求证：平面 平面 ；1AC1BD（2）在线段 上是否存在一点 ，使 与平面 所成的角的正弦值为 ？1DQC1BD269若存在，指出点 的位置，若不存在，说明理由【答案】 （1）见解析；（2）点 在 的中点位置，理由见解析1【解析】 （1）根据三视图可知 平面 ， 为正方形，ABCDA所以 1
18、分ACBD因为 平面 ，所以 ，2 分1又因为 ，所以 平面 4 分1B1AC因为 平面 ，所以平面 平面 5 分B1 1BD（2）以 为坐标原点， ， ， 所在直线分别为 ， ， 轴建立空间直角坐AD1xyz标系，如图所示，根据三视图可知 为边长为 2 的正方形， 为边长为 1 的正方形，ABCD1ABCD平面 ，且 1ABCD1A所以 ， ， ， ， ,01,2,0B,20D,C因为 在 上，所以可设 Q1Q 因为 ，1,D所以 1AAD0,2,10,2所以 ，7 分0,2Q8 分C设平面 的法向量为 ，1BD,xyzn根据 ，1,200, ,1n令 ，可得 ，所以 9 分xyzn设 与平
19、面 所成的角为 ，CQ1BD所以 sinco,CQn22269343所以 ，即点 在 的中点位置12 分121D202018华师附中 已知椭圆 的离心率为 ，圆2:1(0)xyEab12与 轴交于点 、 ， 为椭圆 上的动点， ，22:(0)OxyrMNPE2PMNa面积最大值为 PMN 3（1）求圆 与椭圆 的方程；E（2）圆 的切线 交椭圆于点 ，求 的取值范围lAB、 【答案】 （1）圆 的方程为 ，椭圆 的方程为 ；（2） O21xyE2143xy463，【解析】 （1）由题意得 ，解得： 1 分2cabeba因为 ，所以，点 为椭圆的焦点，所以， ，2 分2PMNaMN、 2214r
20、ca设 ，则 ，所以 ，当 时，0,xy0by 0012PSrya 0yb，代入解得 ，所以 ， ，4 分ma132PMNS a3bc所以，圆 的方程为 ，椭圆 的方程为 5 分O21xyE214xy（2）当直线 的斜率存在时，设直线 的方程为 ，l lkm， ，1,Axkm2,Bxk因为直线 与圆相切，所以 ，即 ，l 21m22k联立 ，消去 可得 ，21 43xyky22438410kxm， ， ，7 分2228830m12243k2143xk222 2114mABkxxkk 222231314344kk 9 分2211336344kk令 ，则 ，所以 ， ，2134tk21403tk
21、21336ABt40t所以 ，所以 10 分2416ABt43当直线 的斜率不存在时，直线 的方程为 ，l l1x解得 ， ， ，11 分3,2,3AB综上， 的取值范围是 12 分AB46，212018南平一模 已知定义在区间 上的函数 0,1lnxft0（1）求函数的单调区间；（2）若不等式 恒成立，求 的取值范围e20fx t【答案】 （1）见解析；（2） 1,【解析】 （1） ，1 分221ttxfx当 时， 即 是 上的增函数3 分2t f 0f0,当 时， ，令 得 ，0t21tttxxft0fx2t则 的增区间为 ，减区间为 5 分fx2,t0,t（2）由不等式 ， 恒成立，得不
22、等式 ， 恒成e0fx ,ln2fx 0,立当 时，由（1）知 是 上的增函数， ，t fx,min1lff即当 时，不等式 ， 恒成立7 分2 ln2 0当 时， ， ， ， 8 分02t20,tx0fx2,t0fx令 ，则 ， tu21tu9 分2minlnlfxf u要使不等式 ， 恒成立，l2 0,x只要 211luu令 ， lnng0,u2 22211uu 是 上的减函数，又 ，g0,0g，则 ，即 ，解得 ，故 ，11 分1u 1u 21t t 12t综合，得 ，即 的取值范围是 12 分t t,请 考 生 在 22、 23 题 中 任 选 一 题 作 答 ,如 果 多 做 ,则
23、按 所 做 的 第 一 题 计 分 。222018龙岩质检 选修 4-4：坐标系与参数方程以直角坐标系的原点 为极点， 轴的正半轴为极轴建立极坐标系，已知直线 的极坐Ox l标方程为 ，曲线 的参数方程是 （ 为参数） 2sin306C2cos inxy（1）求直线 和曲线 的普通方程；l（2）直线 与 轴交于点 ，与曲线 交于 ， 两点，求 xPABPAB【答案】 （1） 的普通方程为 ， 的普通方程为 ；C24xyl30xy（2） 3【解析】 （1） ，2sin306化为 ，即 的普通方程为 ，3icol30xy消去 ，得 的普通方程为 5 分2s inxyC24（2）在 中，令 得 ，3
24、0y0y3,P ，倾斜角 ，k56 的参数方程可设为 ，即 ，l3cos 50in6xty32 1xty代入 得 ， ，方程有两解，24xy23tt70， ， ， 同号，123t125012t10 分PABt2t232018滁州期末 选修 4-5：不等式选讲已知函数 108fx（1）解关于 的不等式 ；21fx（2）若 ，求实数 的取值范围434faaa【答案】 （1） ；（2） | x6，【解析】 （1） 可化为 ，所以 ，018f1x21x所以 ，所以所求不等式的解集为 5 分2x| 2（2）因为函数 在 上单调递增，1208fx， ， 431a241a 24341fafa所以所以 ，所以 ，所以 2026即实数 的取值范围是 10 分a6，欢迎访问“ 高中试卷网”http:/sj.fjjy.org
