2018年普通高等学校招生全国统一考试理科数学仿真试卷（二）学生版

1、绝 密 启 用 前2018 年 普 通 高 等 学 校 招 生 全 国 统 一 考 试 仿 真 卷理科数学（二）本 试 题 卷 共 8 页 ， 23 题 （ 含 选 考 题 ） 。 全 卷 满 分 150 分 。 考 试 用 时 120 分 钟 。祝 考 试 顺 利 注 意 事 项 ：1、 答 题 前 ， 先 将 自 己 的 姓 名 、 准 考 证 号 填 写 在 试 题 卷 和 答 题 卡 上 ， 并 将 准 考 证 号 条 形 码 粘贴 在 答 题 卡 上 的 指 定 位 置 。 用 2B 铅 笔 将 答 题 卡 上 试 卷 类 型 A 后 的 方 框 涂 黑 。2、 选 择 题 的 作

2、答 ： 每 小 题 选 出 答 案 后 ， 用 2B 铅 笔 把 答 题 卡 上 对 应 题 目 的 答 案 标 号 涂 黑 。写 在 试 题 卷 、 草 稿 纸 和 答 题 卡 上 的 非 答 题 区 域 均 无 效 。3、 填 空 题 和 解 答 题 的 作 答 ： 用 签 字 笔 直 接 答 在 答 题 卡 上 对 应 的 答 题 区 域 内 。 写 在 试 题 卷 、草 稿 纸 和 答 题 卡 上 的 非 答 题 区 域 均 无 效 。4、 选 考 题 的 作 答 ： 先 把 所 选 题 目 的 题 号 在 答 题 卡 上 指 定 的 位 置 用 2B 铅 笔 涂 黑 。 答 案 写在

3、 答 题 卡 上 对 应 的 答 题 区 域 内 ， 写 在 试 题 卷 、 草 稿 纸 和 答 题 卡 上 的 非 答 题 区 域 均 无 效 。5、 考 试 结 束 后 ， 请 将 本 试 题 卷 和 答 题 卡 一 并 上 交 。第 卷一 、 选 择 题 ： 本 大 题 共 12 小 题 ， 每 小 题 5 分 ， 在 每 小 题 给 出 的 四 个 选 项 中 ， 只 有一 项 是 符 合 题 目 要 求 的 。12018渭南质检 设 是虚数单位，若复数 ，则 的共轭复数为（ ）i i1zzA B C Di212i21i222018吉林实验中学 若双曲线 的一个焦点为 ，则 （ ）2y

4、xm3,0mA B C D896432018菏泽期末 将函数 的图像向左平移 个单位后，得到函数sin24yx的图像，则 （ ）fx12f班级 姓名 准考证号 考场号 座位号 此卷只装订不密封A B C D26436432242018晋城一模 函数 ， 的值域为 ，在区间 上随机取12xf0,1,一个数 ，则 的概率是（ ）xDA B C D1123452018济南期末 记 ，则7 27012xaxaax012a的值为（ ）6aA1 B2 C129 D218862018昆明一中 一个几何体的三视图如图所示，则该几何体的体积为（ ）A B C D88316320372018漳州调研 九章算术是我

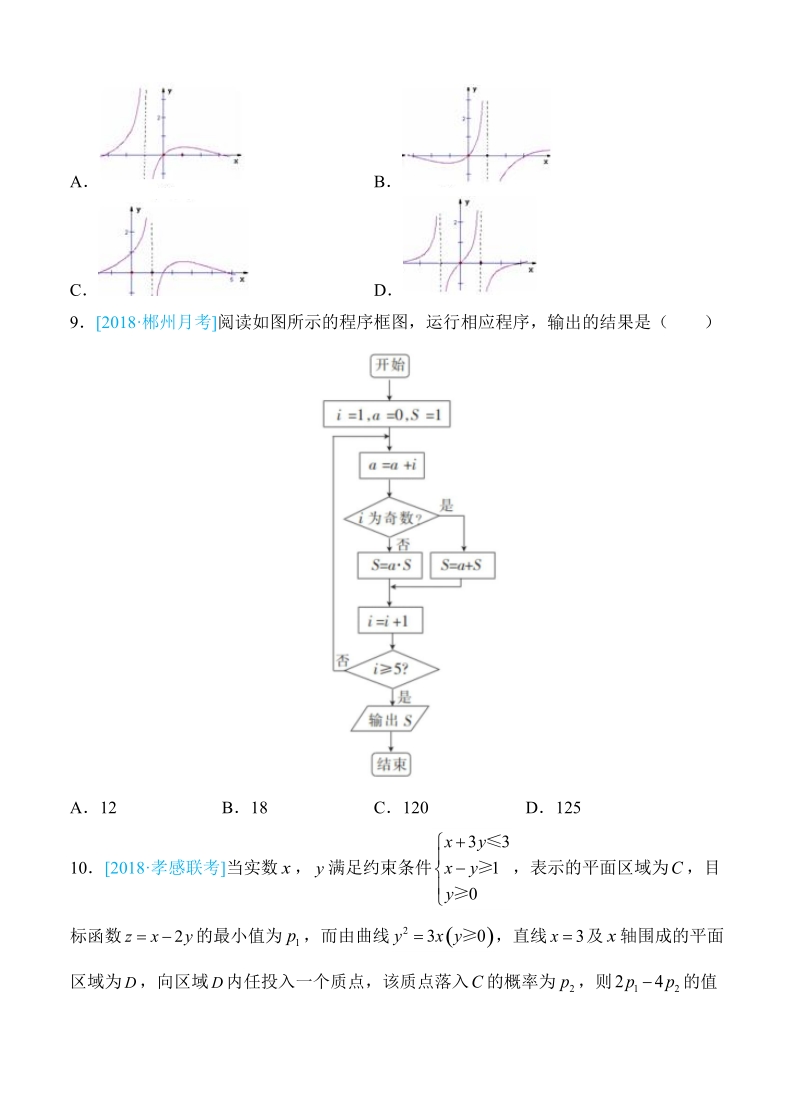
5、国古代的数学名著，书中有如下问题：“今有大夫、不更、簪裹、上造、公士，凡五人，共猎得五鹿，欲以爵次分之，问各得几何？”其意思：“共有五头鹿，5 人以爵次进行分配（古代数学中“以爵次分之”这种表述，一般表示等差分配，在本题中表示等差分配） ”在这个问题中，若大夫得“一鹿、三分鹿之二” ，则簪裹得（ ）A一鹿、三分鹿之一 B一鹿C三分鹿之二 D三分鹿之一82018周口期末 函数 的部分图像大致为（ ）sin1xyA BC D92018郴州月考 阅读如图所示的程序框图，运行相应程序，输出的结果是（ ）A12 B18 C120 D125102018孝感联考 当实数 ， 满足约束条件 ，表示的平面区域为

6、 ，目xy310xy C标函数 的最小值为 ，而由曲线 ，直线 及 轴围成的平面2zxy1p23xy 3x区域为 ，向区域 内任投入一个质点，该质点落入 的概率为 ，则 的值DC2p124p为（ ）A B C D12233543112018德州期末 已知点 是抛物线 ： 的焦点，点 为抛物线 的对称1F2xpy2FC轴与其准线的交点，过 作抛物线 的切线，切点为 ，若点 恰好在以 ， 为焦2 A12点的双曲线上，则双曲线的离心率为（ ）A B C D6212162122018天津期末 已知函数 （其中 是自然对数的底数） ，若当 时，exfe0x恒成立，则实数 的取值范围为（ ）e1xmf m

7、A B C D0,31,31,31,3第 卷本 卷 包 括 必 考 题 和 选 考 题 两 部 分 。 第 (13)(21)题 为 必 考 题 ， 每 个 试 题 考 生 都必 须 作 答 。 第 (22)(23)题 为 选 考 题 ， 考 生 根 据 要 求 作 答 。二 、 填 空 题 ： 本 大 题 共 4 小 题 ， 每 小 题 5 分 。132018镇江期末 已知 ， ，则“ ”是直线 与直线xyR1a10axy平行的_条件（从“充分不必要” “必要不充分” “充分必要” “既10xay不充分也不必要”中选择一个）142018长沙一模 若当 时，函数 取得最小值，则x3cosinfx

8、x_cos152018衡水金卷 在矩形 中， ， 边 上（包含 、 ）上ABCD21ADCD的动点 与 延长线上（包含点 ）的动点 满足 ，则 的最小值为PCBQPBAPQ_162018闽侯四中 设数列 满足 ， ，且 ，若 表示na126a212nnax不超过 的最大整数，则 _x12201707三 、 解 答 题 ： 解 答 应 写 出 文 字 说 明 、 证 明 过 程 或 演 算 步 骤 。172018长郡中学 已知在 中，角 ， ， 的对边分别为 ， ， ，且ABC BCabcsincos0aBbA（1）求角 的大小：（2）若 ， 求 的面积52182018济南期末 基于移动互联技术

9、的共享单车被称为“新四大发明” 之一，短时间内就风靡全国，带给人们新的出行体验某共享单车运营公司的市场研究人员为了解公司的经营状况，对该公司最近六个月内的市场占有率进行了统计，结果如下表：月份 2017.8 2017.9 2017.10 2017.11 2017.12 2018.1月份代码 x1 2 3 4 5 6市场占有率 %y11 13 16 15 20 21（1）请在给出的坐标纸中作出散点图，并用相关系数说明可用线性回归模型拟合月度市场占有率 与月份代码 之间的关系；x（2）求 关于 的线性回归方程，并预测该公司 2018 年 2 月份的市场占有率；yx（3）根据调研数据，公司决定再采购

10、一批单车扩大市场，现有采购成本分别为 1000 元/辆和 800 元/辆的 ， 两款车型报废年限各不相同考虑到公司的经济效益，该公司AB决定先对两款单车各 100 辆进行科学模拟测试，得到两款单车使用寿命频数表如下：经测算，平均每辆单车每年可以为公司带来收入 500 元不考虑除采购成本之外的其他成本，假设每辆单车的使用寿命都是整数年，且用频率估计每辆单车使用寿命的概率，以每辆单车产生利润的期望值为决策依据如果你是该公司的负责人，你会选择采购哪款车型？参考数据： ， ， 6217.5iix6135iiixy1036.5参考公式：相关系数 ；2211niiini ii irxy回归直线方程为 ，其

11、中 ， yba21iiiniixbaybx192018南宁二中 如图，四棱锥 中， 为正三角形， ，PABCDP /ABCD， ， ， 为棱 的中点2ABCD90AE（1）求证：平面 平面 ；PABCDE（2）若直线 与平面 所成角为 ，求二面角 的余弦值45ADEC202018南宁二中 如图，曲线 与正方形 ： 的边2:1(0,)xyEmnL4xy界相切（1）求 的值；mn（2）设直线 交曲线 于 ， ，交 于 ， ，是否存在这样的曲线 ，:lyxbEABLCDE使得 ， ， 成等差数列？若存在，求出实数 的取值范围；若不存在，请说CABDb明理由212018达州期末 已知函数 2ln0fx

12、ax（1）讨论函数 在 上的单调性；fx,a（2）证明： 且 322ln 32ln160xx请 考 生 在 22、 23 题 中 任 选 一 题 作 答 ,如 果 多 做 ,则 按 所 做 的 第 一 题 计 分 。222018吕梁一模 直角坐标系 中，曲线 的参数方程为 （ 为参xOy1C1cos inxy数） ，曲线 2:13xCy（1）在以 为极点， 轴的正半轴为极轴的极坐标系中，求 ， 的极坐标方程；O1C2（2）射线 与 异于极点的交点为 ，与 的交点为 ，求 03 1A2BA222018 邢台期末 选修 4-5：不等式选讲已知函数 3fx（1）若 ，求 的取值范围；29ttt（2）

13、若存在 ，使得 成立，求 的取值范围,4x23fxa a绝密 启用前2018 年 普 通 高 等 学 校 招 生 全 国 统 一 考 试 仿 真 卷理 科 数 学 （ 二 ） 答 案第 卷一 、 选 择 题 ： 本 大 题 共 12 小 题 ， 每 小 题 5 分 ， 在 每 小 题 给 出 的 四 个 选 项 中 ， 只 有一 项 是 符 合 题 目 要 求 的 。1D 2B 3D 4B 5C 6B7B 8B 9C 10B 11C 12B第 卷本 卷 包 括 必 考 题 和 选 考 题 两 部 分 。 第 (13)(21)题 为 必 考 题 ， 每 个 试 题 考 生 都必 须 作 答 。

14、第 (22)(23)题 为 选 考 题 ， 考 生 根 据 要 求 作 答 。二 、 填 空 题 ： 本 大 题 共 4 小 题 ， 每 小 题 5 分 。13充要 14 15 1610342016三 、 解 答 题 ： 解 答 应 写 出 文 字 说 明 、 证 明 过 程 或 演 算 步 骤 。17 【答案】 （1） ；（2）4A【解析】 （1）在 中，由正弦定理得 1 分BC sinsico0ABA即 ，又角 为三角形内角， ，sincos0 所以 ，3 分A即 ，4 分2si4又因为 ，所以 6 分0,4A（2）在 中，由余弦定理得： ，BC 22cosabA则 7 分204c即 8

15、分2160解得 （舍）或 10 分c42c所以 12 分2S18 【答案】 （1）见解析；（2） ，23%；（3）见解析29yx【解析】 （1）散点图如图所示：1 分， ，13652016y62176iiy ，1221niiini ii ixyr35350.96.所以两变量之间具有较强的线性相关关系，3 分故可用线性回归模型拟合两变量之间的关系（2） ，4 分1231 527.niiiiixyb又 ，3456.x ，5 分192.ayb回归直线方程为 6 分29yx2018 年 2 月的月份代码 ， ，72793y所以估计 2018 年 2 月的市场占有率为 23%7 分（3）用频率估计概率，

16、 款单车的利润 的分布列为：AX （元） 9 分50.1.350.410.235EX款单车的利润 的分布列为：BY （元） 11 分30.1520.470.3512.40EY以每辆单车产生利润的期望值为决策依据，故应选择 款车型12 分B19 【答案】 （1）证明见解析；（2） 19【解析】 （1）取 中点 ，连接 ， APFEDF为 中点， ，又 ， ，EB1/=2EB/=2CAB/=EF为平行四边形，2 分CDF3 分/又 为正三角形， ，从而 ，4 分PA PADFP又 ， ， 平面 ，5 分CECE又 平面 ， 平面 平面 6 分B（2） ， ，又 ， ， 平/DBADAB面 平面 为

17、 与平面 所成的角，即 ，PAPAP45CPDC以 为原点，建系如图，设 ，则 ， ， ，A4AD8,0B,23P0,4D，8 分4,13E， 设 为平面 的法向量，,0,xyznAE则 ，令 ，得 ，10 分34AxyzDn4z3,04由（1）知， 为平面 的一个法向量11 分20,1PCDE，即二面角 的余弦值为 ，即二面角57cos9AnAC25719的余弦值为 12 分DEC2120 【答案】 （1） ；（2） 6mn823b 【解析】 （1）由题 ，得 ，14xy2160nmxmn有 ，2 分26460mn化简的 又 ， ，所以 从而有 ；4 分016mn（2）由 ，ABCD得 ，即

18、 5 分342AB423AB由 ，得 ，21xymnb220mxbmn由 可得 ，22440n216且 ， ，7 分12xnm12bx所以 ，8 分2241643nABka可得 ，316bn从而 ，2382mn所以 ，即有 ，10 分2189b 3b 符合 ，故当实数 的取值范围是 时，存在直线 和曲线 ，26mn823b lE使得 ， ， 成等差数列12 分CABD21 【答案】 （1）见解析；（2）见解析【解析】 （1）解： ， 2lnfxax221axf令 ，得 ，1 分20xaf20当 ，即 时，则 ，2 1 fx在 上单调递增；3 分fx,a当 ，即 时，令 ，得 ；令 ，得 20f

19、x2a0fx2ax在 上单调递减，在 上单调递增fx2,a2,a综上，当 时， 在 上单调递增；01 fx当 时， 在 上单调递减，在 上单调递增5 分f2, 2,（2）证明：先证 当 时， ，3lnxx 1alnfx由（1）可得当 时， ， 单调递减；010f当 时， ， 单调递增xfxx， ， 8 分minfln 322lnxx再证 32l160xx设 ，2g则 ，当且仅当 时取等号3232ln160xxx 1x设 ，则 ，160h()382hx当 时， ， 单调递增；2xx令 ，得 时， ， 单调递减020x ，minhxgh 又此不等式中两个等号的成立条件不同，故 ，0gx从而 得证3

20、2l160xx综上可得 且 12 分2n 32ln160x请 考 生 在 22、 23 题 中 任 选 一 题 作 答 ,如 果 多 做 ,则 按 所 做 的 第 一 题 计 分 。22 【答案】 （1）曲线 的极坐标方程为 ，曲线 的极坐标方程为1C2cos2C；（2） 2sin3123015AB【解析】 （1）曲线 ： （ 为参数）化为普通方程为 ，1Ccos inxy 2xy所以曲线 的极坐标方程为 ，3 分12曲线 的极坐标方程为 5 分21si3（2）射线 与曲线 的交点的极径为 ，7 分03 C12cos3射线 与曲线 的交点的极径满足 ， 22in解得 ，9 分2305所以 10 分121AB23 【答案】 （1） ；（2） 5t4,0a【解析】 （1）由 得 ，9f329tt ，或 ，或 ，3 分329tt 32t3tt解得 5 分15（2）当 时， ，6 分2,4x23fxaxa存在 ，使得 即 成立，6 62x 存在 ，使得 成立，8 分2,4x3xa ， 10 分6a ,0a欢迎访问“ 高中试卷网”http:/sj.fjjy.org