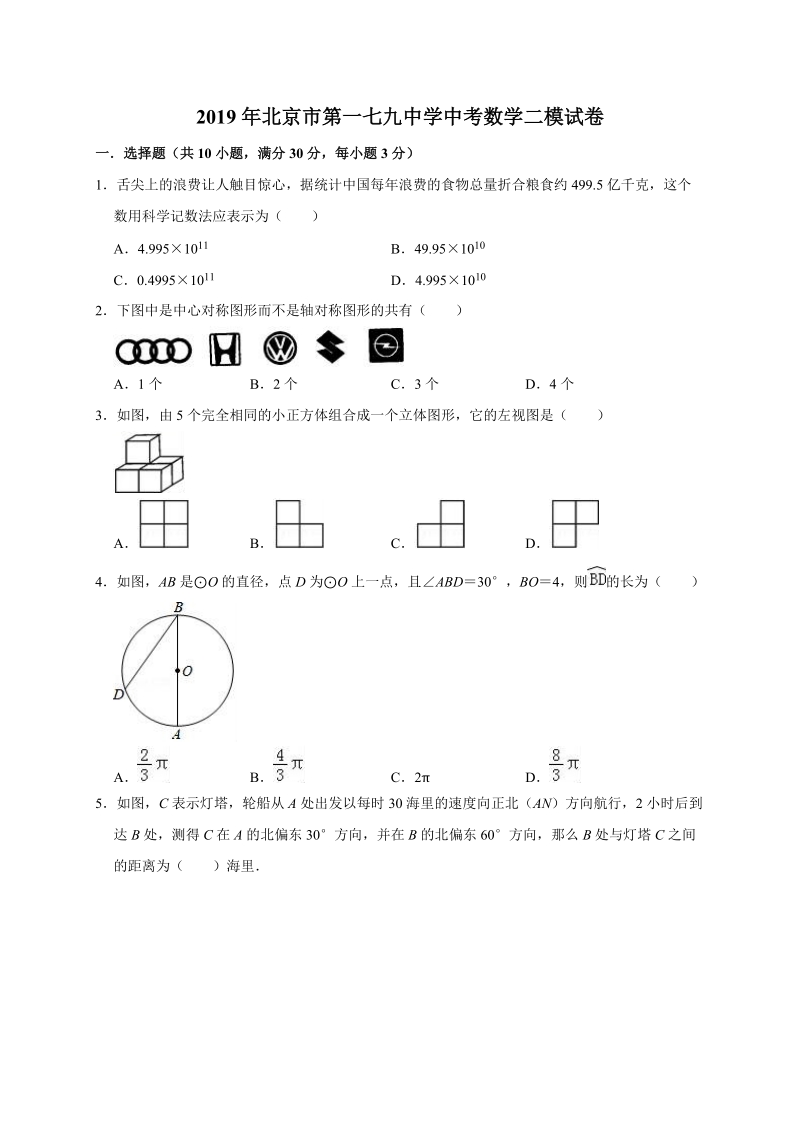
1、2019 年北京市第一七九中学中考数学二模试卷一选择题（共 10 小题，满分 30 分，每小题 3 分）1舌尖上的浪费让人触目惊心，据统计中国每年浪费的食物总量折合粮食约 499.5 亿千克，这个数用科学记数法应表示为（ ）A4.99510 11 B49.9510 10C0.499510 11 D4.995 10102下图中是中心对称图形而不是轴对称图形的共有（ ）A1 个 B2 个 C3 个 D4 个3如图，由 5 个完全相同的小正方体组合成一个立体图形，它的左视图是（ ）A B C D4如图，AB 是O 的直径，点 D 为O 上一点，且ABD30，BO 4，则 的长为（ ）A B C2 D
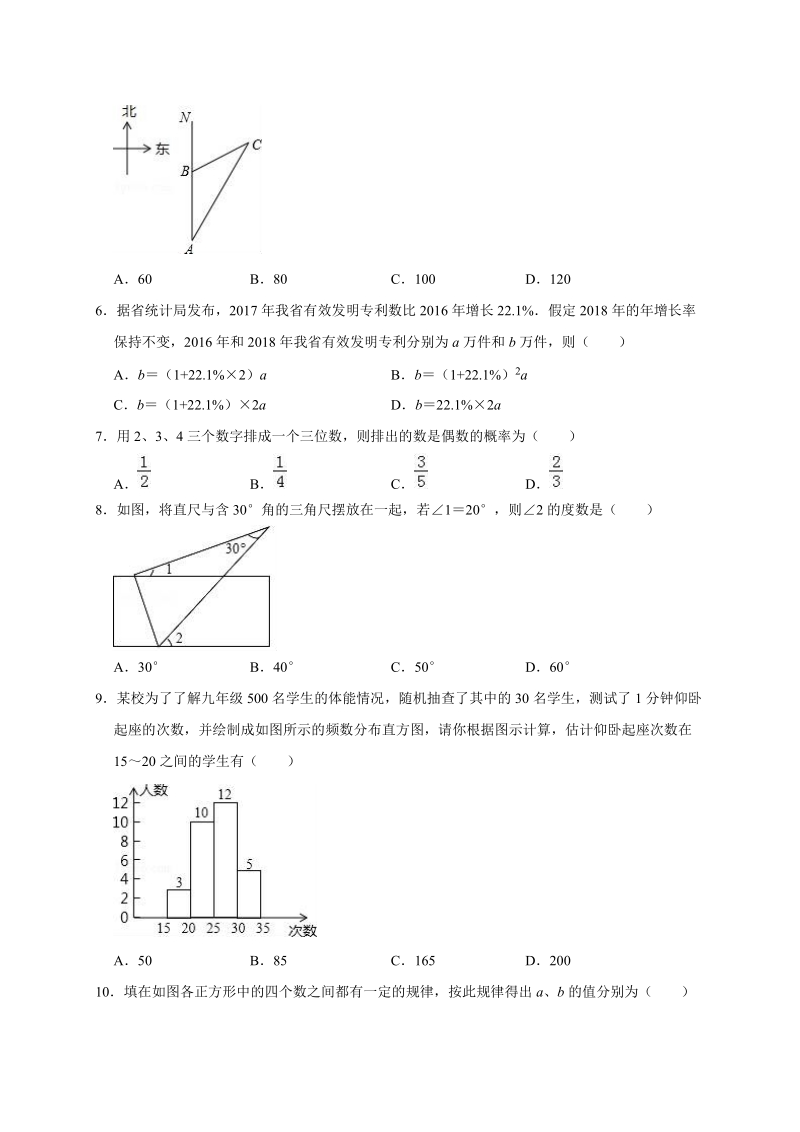
2、5如图，C 表示灯塔，轮船从 A 处出发以每时 30 海里的速度向正北（AN ）方向航行，2 小时后到达 B 处，测得 C 在 A 的北偏东 30方向，并在 B 的北偏东 60方向，那么 B 处与灯塔 C 之间的距离为（ ）海里A60 B80 C100 D1206据省统计局发布，2017 年我省有效发明专利数比 2016 年增长 22.1%假定 2018 年的年增长率保持不变，2016 年和 2018 年我省有效发明专利分别为 a 万件和 b 万件，则（ ）Ab（1+22.1%2）a Bb（1+22.1%） 2aCb（1+22.1%）2a Db22.1%2a7用 2、3、4 三个数字排成一个三
3、位数，则排出的数是偶数的概率为（ ）A B C D8如图，将直尺与含 30角的三角尺摆放在一起，若120，则2 的度数是（ ）A30 B40 C50 D609某校为了了解九年级 500 名学生的体能情况，随机抽查了其中的 30 名学生，测试了 1 分钟仰卧起座的次数，并绘制成如图所示的频数分布直方图，请你根据图示计算，估计仰卧起座次数在1520 之间的学生有（ ）A50 B85 C165 D20010填在如图各正方形中的四个数之间都有一定的规律，按此规律得出 a、b 的值分别为（ ）A10、91 B12、91 C10、95 D12、95二填空题（共 6 小题，满分 18 分，每小题 3 分）1
4、1计算：（ ） 01 12分解因式：4m 216n 2 13不等式 1 的解集是 14已知在反比例函数 y 图象的任一分支上，y 都随 x 的增大而增大，请写出一个符合条件的 k 的值 15如图，计划把水从河中引到水池 A 中，先过点 A 作 ABCD，垂足为点 B，然后沿 AB 开渠，能使所开的渠道最短，这样设计的依据是 16如图，定点 A（2，0），动点 B 在直线 yx 上运动，当线段 AB 最短时，点 B 的坐标为 三解答题（共 7 小题）17如图，在由边长为 1 个单位长度的小正方形组成的 1010 网格中，已知点 O，A，B 均为网格线的交点（1）在给定的网格中，以点 O 为位似中
5、心，将线段 AB 放大为原来的 2 倍，得到线段 A1B1（点A，B 的对应点分别为 A1，B 1），画出线段 A1B1；（2）将线段 A1B1 绕点 B1 逆时针旋转 90得到线段 A2B1，画出线段 A2B1；（3）以 A，A 1，B 1，A 2 为顶点的四边形 AA1B1A2 的面积是 个平方单位18A、B 两地相距 450 千米，甲，乙两车分别从 A、B 两地同时出发，相向而行已知甲车速度为120 千米/时，乙车速度为 80 千米/ 时，经过多少小时两车相距 50 千米？19如图，在 RtABC 中，C90，BC6cm，AC8cm，点 P 从点 C 开始沿射线 CA 方向以1cm/s
6、的速度运动；同时，点 Q 也从点 C 开始沿射线 CB 方向以 3cm/s 的速度运动（1）几秒后PCQ 的面积为 3cm2？此时 PQ 的长是多少？（结果用最简二次根式表示）（2）几秒后以 A、B、P 、Q 为顶点的四边形的面积为 22cm2？20体育节中，学校组织八年级学生举行定点投篮比赛，要求每班选派 10 名队员参加下面是一班和二班参赛队员定点投篮比赛成绩的折线统计图（每人投篮 10 次，每投中一次记 1 分），请根据图中信息回答下列问题：（1）将下表中一、二班队员投篮比赛成绩的有关数据补充完整：平均数/分 中位数/分 众数/分一班 8.2 8.5 二班 8.0 8（2）观察统计图，判
7、断一班、二班 10 名队员投篮成绩的方差的大小关系：s 一班 2 s 二班 2；（3）综合（1）、（2）中的数据，选择一个方面对一班、二班 10 名队员定点投篮比赛成绩进行评价例如：从两班成绩的平均数看，一班成绩高于二班，除此之外，你的评价是：21如图，点 A 的坐标为（3，0），点 C 的坐标为（0，4），OABC 为矩形，反比例函数 的图象过 AB 的中点 D，且和 BC 相交于点 E，F 为第一象限的点，AF12，CF13（1）求反比例函数 和直线 OE 的函数解析式；（2）求四边形 OAFC 的面积？22如图，抛物线 yx 2+bx+c 与 x 轴交于点 A 和 B（3，0），与 y
8、轴交于点 C（0，3）（1）求抛物线的解析式；（2）若点 M 是抛物线上在 x 轴下方的动点，过 M 作 MNy 轴交直线 BC 于点 N，求线段 MN的最大值；（3）E 是抛物线对称轴上一点，F 是抛物线上一点，是否存在以 A，B，E，F 为顶点的四边形是平行四边形？若存在，请直接写出点 F 的坐标；若不存在，请说明理由23定义：数学活动课上，乐老师给出如下定义：有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形理解：（1）如图 1，已知 A、B、C 在格点（小正方形的顶点）上，请在方格图中画出以格点为顶点，AB、BC 为边的两个对等四边形 ABCD；（2）如图 2，在圆内接四边形 A
9、BCD 中，AB 是 O 的直径，AC BD 求证：四边形 ABCD 是对等四边形；（3）如图 3，在 RtPBC 中，PCB90，BC11，tanPBC ，点 A 在 BP 边上，且AB13用圆规在 PC 上找到符合条件的点 D，使四边形 ABCD 为对等四边形，并求出 CD 的长2019 年北京市第一七九中学中考数学二模试卷参考答案与试题解析一选择题（共 10 小题，满分 30 分，每小题 3 分）1【分析】科学记数法的表示形式为 a10n 的形式，其中 1|a| 10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值1
10、 时，n 是非负数；当原数的绝对值1 时，n 是负数【解答】解：将 499.5 亿用科学记数法表示为：4.99510 10故选：D【点评】此题考查了科学记数法的表示方法科学记数法的表示形式为 a10n 的形式，其中1|a| 10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值2【分析】根据轴对称图形与中心对称图形的概念求解【解答】解：第一个图形，既是中心对称图形，又是轴对称图形，故错误；第二个图形，是轴对称图形，不是中心对称图形，故错误；第三个图形，是轴对称图形，不是中心对称图形，故错误；第四、五个是中心对称图形而不是轴对称图形，故正确故选：B【点评】掌握好中心对称与轴对称的概念：轴
11、对称的关键是寻找对称轴，两边图象折叠后可重合，中心对称是要寻找对称中心，旋转 180度后与原图重合3【分析】找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在左视图中【解答】解：从左面看易得第一层有 2 个正方形，第二层最左边有一个正方形故选：B【点评】本题考查了三视图的知识，左视图是从物体的左面看得到的视图4【分析】先计算圆心角为 120，根据弧长公式 ，可得结果【解答】解：连接 OD，ABD30，AOD 2 ABD60，BOD 120 ， 的长 ，故选：D【点评】本题考查了弧长的计算和圆周角定理，熟练掌握弧长公式是关键，属于基础题5【分析】将方位表示的角度转化为题目中对应角的度数，
12、再根据等腰三角形的性质即可得到答案【解答】解：NBCA +C ，NBC60，A30C30ABC 为等腰三角形船从 A 到 B 以每小时 30 海里的速度走了 2 小时，ABBC60 海里故选：A【点评】考查了等腰三角形的判定与性质，本题可用直角三角形性质解，但用等腰三角形更为简单，可根据自己情况灵活选择6【分析】根据 2016 年的有效发明专利数（1+年平均增长率） 22018 年的有效发明专利数【解答】解：因为 2016 年和 2018 年我省有效发明专利分别为 a 万件和 b 万件，所以b（1+22.1%） 2a故选：B【点评】考查了列代数式，掌握 2 次增长或下降之类方程的等量关系是解决
13、本题的关键7【分析】首先利用列举法可得：用 2，3，4 三个数字排成一个三位数，等可能的结果有：234，243，324，342，423，432；且排出的数是偶数的有：234、324、342、432，然后直接利用概率公式求解即可求得答案【解答】解：用 2，3，4 三个数字排成一个三位数，等可能的结果有：234，243，324，342，423，432；排出的数是偶数的有：234、324、342、432；排出的数是偶数的概率为： 【点评】此题考查了列举法求概率用到的知识点为：概率所求情况数与总情况数之比8【分析】先根据三角形外角的性质求出BEF 的度数，再根据平行线的性质得到2 的度数【解答】解：如
14、图，BEF 是AEF 的外角，120，F30，BEF 1+F50，ABCD，2BEF50，故选：C【点评】本题主要考查了平行线的性质，解题的关键是掌握三角形外角的性质9【分析】用被抽查的 30 名学生中 1520 之间的学生所占的百分数乘以九年级学生总人数，计算即可得解【解答】解：500 50故选：A【点评】本题考查读频数分布直方图的能力和利用统计图获取信息的能力；利用统计图获取信息时，必须认真观察、分析、研究统计图，才能作出正确的判断和解决问题10【分析】分析前三个正方形，发现“右上的数左上的数+3，左下的数左上的数+4，右下的数右上的数左下的数+1”，依此即可得出 a、b、c 的值【解答】
15、解：分析正方形中的四个数：第一个正方形中 0+33，0+44，34+1 13；第二个正方形中2+35，2+46，56+1 31；第三个正方形中 4+37，4+48，78+1 57c6+39，a6+410，b910+191故选：A【点评】本题考查了规律型中的数字的变换类，解题的关键是分析正方形中四个数找出它们之间的关系“右上的数左上的数+3，左下的数左上的数+4，右下的数右上的数左下的数+1”本题属于基础题，难度不大，解决该题型题目时，根据给定的正方形中的 4 个数，找出它们之间的关系是关键二填空题（共 6 小题，满分 18 分，每小题 3 分）11【分析】根据零指数幂：a 01（a0）进行计算
16、即可【解答】解：原式110，故答案为：0【点评】此题主要考查了零指数幂，关键是掌握 a01（a0）12【分析】原式提取 4 后，利用平方差公式分解即可【解答】解：原式4（m+2n）（m 2n）故答案为：4（m+2n）（m2n）【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键13【分析】根据解一元一次不等式得基本步骤依次计算可得【解答】解：去分母，得：x82，移项，得：x2+8，合并同类项，得：x10，故答案为：x10【点评】本题考查了解一元一次不等式：有分母先去分母，再去括号，然后进行移项，把含未知数的项移到不等式的左边，再进行合并同类项，最后把未知数的系数
17、化为 1 可得到不等式的解集14【分析】根据“在反比例函数 y 图象的任一分支上，y 都随 x 的增大而增大”，得到关于 k 的一元一次不等式，解之即可【解答】解：根据题意得：1k0，解得：k1，故答案为：k1【点评】本题考查了反比例函数图象上点的坐标特征和反比例函数的性质，正确掌握反比例函数的增减性是解题的关键15【分析】根据垂线段的性质，可得答案【解答】解：先过点 A 作 ABCD，垂足为点 B，然后沿 AB 开渠，能使所开的渠道最短，这样设计的依据是垂线段最短；故答案为：垂线段最短【点评】本题考查了垂线段，利用垂线段的性质是解题关键16【分析】过 A 作 AD直线 yx，过 D 作 DE
18、x 轴于 E，即当 B 点和 D 点重合时，线段 AB的长最短，求出DOAOADEDOEDA45，OA2，求出 OEDE1，求出 D的坐标即可【解答】解：过 A 作 AD直线 yx，过 D 作 DEx 轴于 E，则DOA OADEDOEDA45，A（2，0），OA2，OEDE 1，D 的坐标为（1，1），即动点 B 在直线 yx 上运动，当线段 AB 最短时，点 B 的坐标为（1，1），故答案为：（1，1）【点评】本题考查了等腰直角三角形，垂线段最短，坐标与图形性质的应用，解此题的关键求出符合条件的点的位置三解答题（共 7 小题）17【分析】（1）以点 O 为位似中心，将线段 AB 放大为原来
19、的 2 倍，即可画出线段 A1B1；（2）将线段 A1B1 绕点 B1 逆时针旋转 90得到线段 A2B1，即可画出线段 A2B1；（3）连接 AA2，即可得到四边形 AA1B1A2 为正方形，进而得出其面积【解答】解：（1）如图所示，线段 A1B1 即为所求；（2）如图所示，线段 A2B1 即为所求；（3）由图可得，四边形 AA1B1A2 为正方形，四边形 AA1B1A2 的面积是（ ） 2（ ） 220故答案为：20【点评】此题主要考查了位似变换以及旋转的性质以及勾股定理等知识的运用，利用相似变换的性质得出对应点的位置是解题关键18【分析】应该有两种情况，第一次应该还没相遇时相距 50 千
20、米，第二次应该是相遇后交错离开相距 50 千米，根据路程速度时间，可列方程求解【解答】解：设第一次相距 50 千米时，经过了 x 小时（120+80）x45050x2设第二次相距 50 千米时，经过了 y 小时（120+80）y450+50y2.5经过 2 小时或 2.5 小时相距 50 千米【点评】本题考查理解题意能力，关键知道相距 50 千米时有两次以及知道路程速度时间，以路程做为等量关系可列方程求解19【分析】（1）设出运动所求的时间，可将 PC 和 CQ 的长表示出来，代入三角形面积公式，列出等式，可将时间求出；（2）需要对点 P 的不同位置进行分类讨论：当 P 在线段 AC 上，Q
21、在线段 BC 上时，0t2S 四边形 APQBS ABC SPQC ，得，当 P 在线段 AC 上，Q 在线段 BC 延长线上时，2t 8，S 四边形 APBQS AQC S PBC ；当 P 在线段 AC 的延长线上，Q 在线段 BC 延长线上时，t 8，S 四边形 ABQPS PQC S ABC【解答】解：（1）设 t 秒后 PCQ 的面积为 3 平方厘米，则有 PCt cm ，CQ3t cm，依题意，得： t3t3，t22 （舍去），由勾股定理，得：PQ 答： 秒后PCQ 的面积为 3 平方厘米，此时 PQ 的长是 ；（2） 当 P 在线段 AC 上，Q 在线段 BC 上时，0t 2S
22、四边形 APQBS ABC S PQC，解得 ，当 P 在线段 AC 上，Q 在线段 BC 延长线上时，2t 8，S 四边形 APBQS AQC S PBC9t22，解得 ；当 P 在线段 AC 的延长线上，Q 在线段 BC 延长线上时，t 8，S 四边形 ABQPS PQC S ABC（不符合题意，舍去），（或者得 ， ，都不符合题意，舍去），综上： 或 答，经过 秒或 秒，以 A、B、P、Q 为顶点的四边形的面积为 22cm2【点评】本题考查了一元二次方程的应用此题是根据三角形的面积公式列出一元二次方程，进行求解20【分析】（1）从图中得出两个班的 10 名队员的成绩，分别求得众数、中位数
23、、平均数填表即可；（2）计算出方差，进一步比较得出答案即可；（3）从中位数，众数及方差进一步分析得出答案即可【解答】解：（1）一班 10 名队员投篮成绩：7，10，9，5，8，10，8，6，9，10；平均数：（7+10+9+5+8+10+8+6+9+10）108.2，从小到大排列为：5，6，7，8，8，9，9，10，10，10；中位数为：8.5；众数为：10；二班 10 名队员投篮成绩：8，9，8，8，7，8，9，8，8，7；平均数：（8+9+8+8+7+8+9+8+8+7）108；从小到大排列为：7，7，8，8，8，8，8，8，9，9；中位数为：8；众数为：8；填表如下：平均数/分 中位数/
24、分 众数/分一班 8.2 8.5 10二班 8.0 8 8（2）s 一班 2 （58.2） 2+（68.2） 2+（7 8.2） 2+2（88.2） 2+2（98.2）2+3（108.2） 22.11；s 二班 2 2（78） 2+6（88） 2+2（89） 20.4；所以 s 一班 2s 二班 2；（3）从中位数来看，一班高于二班，从方差来看，二班的稳定性较好，队员的整体水平相差不大，一班队员的个体水平较高【点评】本题考查了平均数，中位数，众数及方差的意义及求法，从图表中得出信息，进一步利用这些知识来评价这组数据是解题关键21【分析】（1）易得点 B 的坐标为（3，4），点 D 的坐标为（3
25、，2），把 D（3，2）代入 ，得 k6，确定反比例函数的解析式；设点 E 的坐标为（m，4），将其代入 ，得 m ，确定点 E 的坐标为（ ，4），然后利用待定系数法可求出直线 OE 的解析式；（2）连接 AC，在 RtOAC 中，OA 3，OC4，利用勾股数易得 AC5，则有AC2+AF25 2+12213 2CF 2，根据勾股定理的逆定理得到 CAF90，于是四边形 OAFC 的面积可化为两个直角三角形的面积进行计算【解答】解：（1）依题意，得点 B 的坐标为（3，4），点 D 的坐标为（3，2），将 D（3，2）代入 ，得 k6反比例函数的解析式为 ；设点 E 的坐标为（m，4），将其
26、代入 ，得 m ，点 E 的坐标为（ ，4），设直线 OE 的解析式为 yk 1x，将（ ，4）代入得 k1 ，直线 OE 的解析式为 y x；（2）连接 AC，如图，在 Rt OAC 中， OA3，OC4，AC5，而 AF12，CF 13AC 2+AF25 2+12213 2CF 2，CAF90，S 四边形 OAFCS OAC +SCAF 34+ 5126+3036【点评】本题考查了反比例函数的性质：点在反比例函数图象上，则点的横纵坐标满足其解析式也考查了待定系数法和勾股定理及其逆定理以及不规则图形面积的计算方法22【分析】（1）由点 B、C 的坐标利用待定系数法即可求出抛物线的解析式；（2
27、）设出点 M 的坐标以及直线 BC 的解析式，由点 B、C 的坐标利用待定系数法即可求出直线BC 的解析式，结合点 M 的坐标即可得出点 N 的坐标，由此即可得出线段 MN 的长度关于 m 的函数关系式，再结合点 M 在 x 轴下方可找出 m 的取值范围，利用二次函数的性质即可解决最值问题；（3）讨论：当以 AB 为对角线，利用 EAEB 和四边形 AFBE 为平行四边形得到四边形 AFBE为菱形，则点 F 也在对称轴上，即 F 点为抛物线的顶点，所以 F 点坐标为（1，4）；当以AB 为边时，根据平行四边形的性质得到 EFAB 4，则可确定 F 的横坐标，然后代入抛物线解析式得到 F 点的纵
28、坐标【解答】解：（1）将点 B（3，0）、C（0，3）代入抛物线 yx 2+bx+c 中，得： ，解得： 故抛物线的解析式为 yx 24x +3（2）设点 M 的坐标为（m，m 24m+3），设直线 BC 的解析式为 ykx+3，把点 B（3，0）代入 ykx+3 中，得：03k+3，解得：k 1，直线 BC 的解析式为 yx+3MNy 轴，点 N 的坐标为（m，m+3）抛物线的解析式为 yx 24x +3（x2） 21，抛物线的对称轴为 x2，点（1，0）在抛物线的图象上，1m3线段 MNm+3（m 24m +3）m 2+3m（m ） 2+ ，当 m 时，线段 MN 取最大值，最大值为 （3
29、）存在点 F 的坐标为（2，1）或（0，3）或（4，3）当以 AB 为对角线，如图 1，四边形 AFBE 为平行四边形，EAEB，四边形 AFBE 为菱形，点 F 也在对称轴上，即 F 点为抛物线的顶点，F 点坐标为（2，1）；当以 AB 为边时，如图 2，四边形 AFBE 为平行四边形，EFAB2，即 F2E2， F1E2，F 1 的横坐标为 0，F 2 的横坐标为 4，对于 yx 24x +3，当 x0 时，y3；当 x4 时，y1616+3 3，F 点坐标为（0，3）或（4，3）综上所述，F 点坐标为（2，1）或（0，3）或（4，3）【点评】本题考查了待定系数法求函数解析式、二次函数图象
30、上点的坐标特征、二次函数的性质、两点间的距离以及等腰三角形的性质，解题的关键是：（1）利用待定系数法求出函数解析式；（2）利用二次函数的性质解决最值问题；（3）注意分类思想的运用23【分析】（1）根据对等四边形的定义，进行画图即可；（2）连接 AC，BD，证明 RtADB RtACB，得到 ADBC ，又 AB 是 O 的直径，所以ABCD，即可解答；（3）根据对等四边形的定义，分两种情况：若 CDAB，此时点 D 在 D1 的位置，CD1AB13；若 ADBC11，此时点 D 在 D2、D 3 的位置，AD 2AD 3BC11；利用勾股定理和矩形的性质，求出相关相关线段的长度，即可解答【解答
31、】解：（1）如图 1 所示（画 2 个即可）（2）如图 2，连接 AC，BD，AB 是O 的直径，ADBACB90，在 Rt ADB 和 RtACB 中，RtADBRtACB，ADBC，又AB 是O 的直径，ABCD，四边形 ABCD 是对等四边形（3）如图 3，点 D 的位置如图所示：若 CDAB，此时点 D 在 D1 的位置，CD 1AB13；若 ADBC 11，此时点 D 在 D2、D 3 的位置，AD 2AD 3BC11，过点 A 分别作 AEBC，AFPC ，垂足为 E，F，设 BEx，tanPBC ，AE ，在 Rt ABE 中，AE 2+BE2AB 2，即 ，解得：x 15，x 25（舍去），BE5，AE12，CEBCBE6，由四边形 AECF 为矩形，可得 AFCE 6，CF AE12，在 Rt AFD2 中， ， ， ，综上所述，CD 的长度为 13、12 或 12+ 【点评】本题主要考查了四边形的综合题，解题的关键是理解并能运用“等对角四边形”这个概念在（3）中注意分类讨论思想的应用、勾股定理的应用
