1、2019 年福建省龙岩市永定县金丰片区中考数学一模试卷一、选择题（每小题 4 分，共 40 分）1下面的图形是天气预报中的图标，其中既是轴对称图形又是中心对称图形的是（ ）A 晴 B 浮尘 C 大雨 D 大雪22017 年北京市在经济发展、社会进步、城市建设、民生改善等方面取得新成绩、新面貌综合实力稳步提升全市地区生产总值达到 280000 亿元，将 280000 用科学记数法表示为（ ）A28010 3 B2810 4 C2.810 5 D0.2810 63下列计算正确的是（ ）Ax 23x 22x 4 B（3x 2） 26x 2Cx 2y2x32x 6y D6x 3y2（3x）2x 2y2
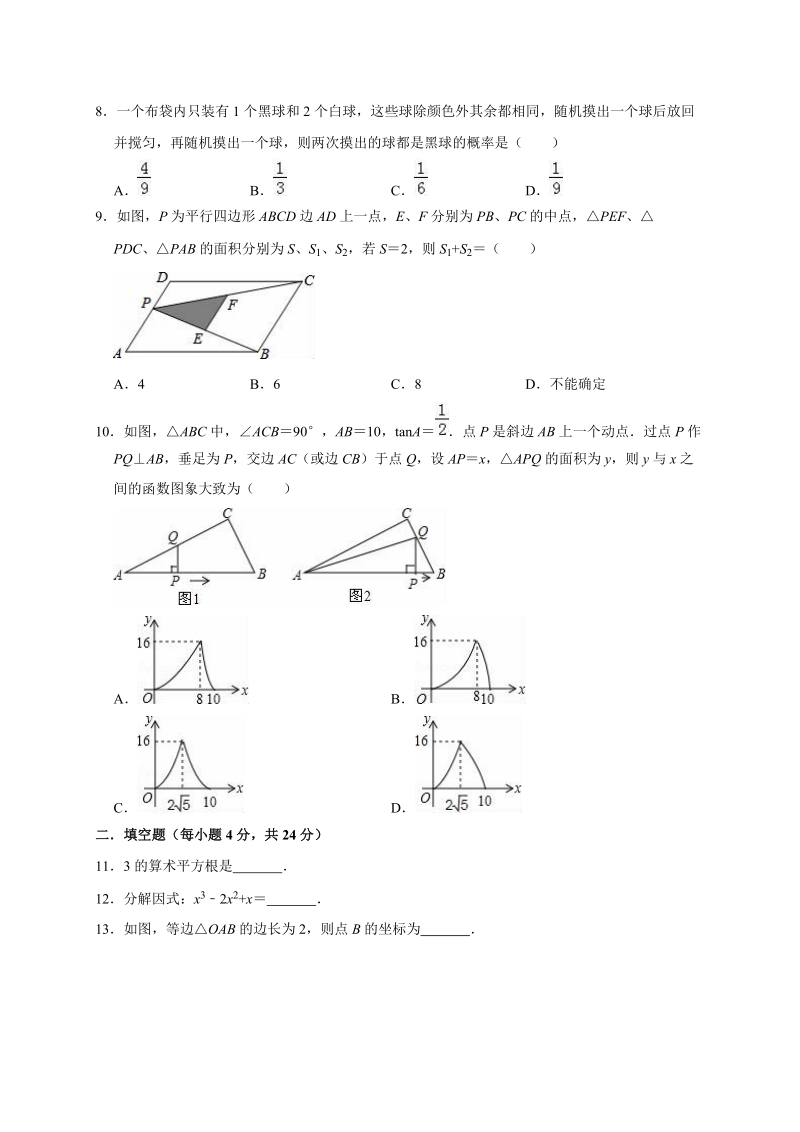
2、4如图，ABCD，DBBC，250，则1 的度数是（ ）A40 B50 C60 D1405一次函数 yx 2 的图象经过点（ ）A（2，0） B（0，0） C（0，2） D（0，2）6如图，在 RtABC 中，ACB90，CD 是 AB 边上的中线，AC8，BC6，则ACD 的正切值是（ ）A B C D7在ABC 中，已知A、B 都是锐角，|sin A |+（ 1tanB） 20，那么C 的度数为（ ）A75 B90 C105 D1208一个布袋内只装有 1 个黑球和 2 个白球，这些球除颜色外其余都相同，随机摸出一个球后放回并搅匀，再随机摸出一个球，则两次摸出的球都是黑球的概率是（ ）A
3、B C D9如图，P 为平行四边形 ABCD 边 AD 上一点，E、F 分别为 PB、PC 的中点，PEF、PDC、PAB 的面积分别为 S、S 1、S 2，若 S2，则 S1+S2（ ）A4 B6 C8 D不能确定10如图，ABC 中，ACB90，AB10，tan A 点 P 是斜边 AB 上一个动点过点 P 作PQAB，垂足为 P，交边 AC（或边 CB）于点 Q，设 APx，APQ 的面积为 y，则 y 与 x 之间的函数图象大致为（ ）A BC D二填空题（每小题 4 分，共 24 分）113 的算术平方根是 12分解因式：x 32x 2+x 13如图，等边OAB 的边长为 2，则点
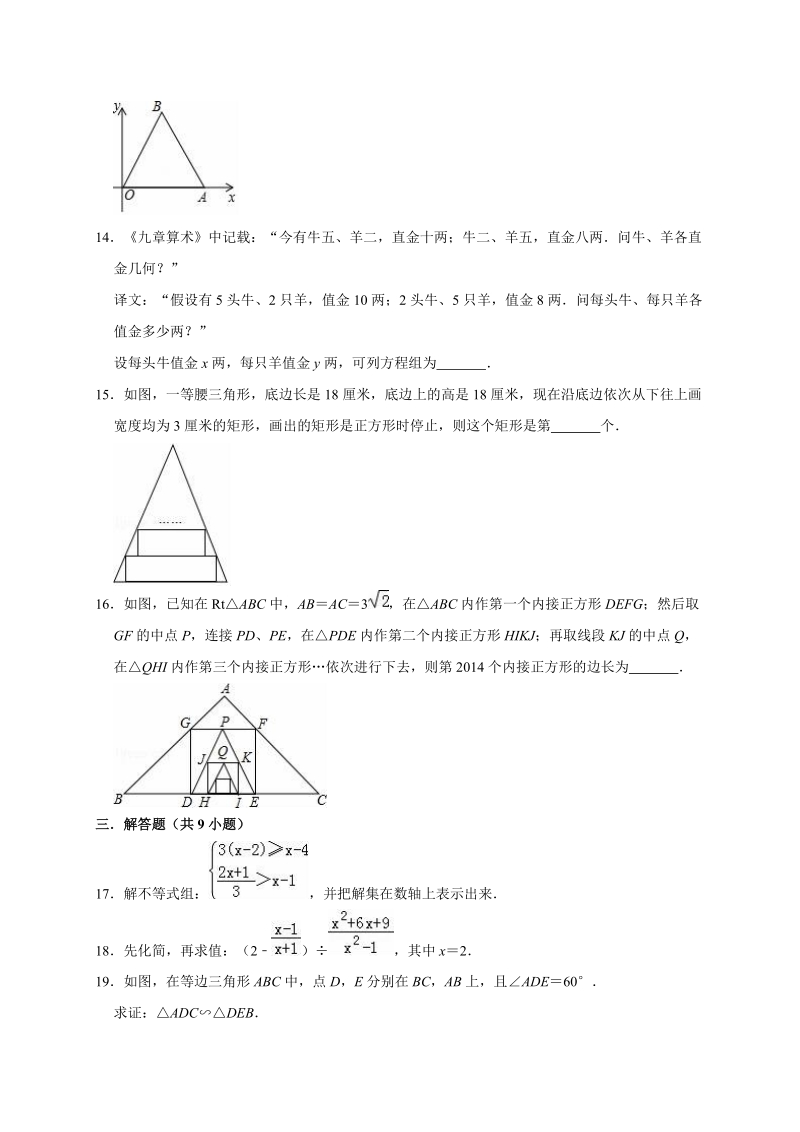
4、B 的坐标为 14九章算术中记载：“今有牛五、羊二，直金十两；牛二、羊五，直金八两问牛、羊各直金几何？”译文：“假设有 5 头牛、2 只羊，值金 10 两；2 头牛、5 只羊，值金 8 两问每头牛、每只羊各值金多少两？”设每头牛值金 x 两，每只羊值金 y 两，可列方程组为 15如图，一等腰三角形，底边长是 18 厘米，底边上的高是 18 厘米，现在沿底边依次从下往上画宽度均为 3 厘米的矩形，画出的矩形是正方形时停止，则这个矩形是第 个16如图，已知在 RtABC 中，ABAC 3 ，在ABC 内作第一个内接正方形 DEFG；然后取GF 的中点 P，连接 PD、PE ，在PDE 内作第二个内
5、接正方形 HIKJ；再取线段 KJ 的中点 Q，在QHI 内作第三个内接正方形依次进行下去，则第 2014 个内接正方形的边长为 三解答题（共 9 小题）17解不等式组： ，并把解集在数轴上表示出来18先化简，再求值：（2 ） ，其中 x219如图，在等边三角形 ABC 中，点 D，E 分别在 BC，AB 上，且ADE60求证：ADCDEB20已知圆锥的底面半径为 3，母线长为 6，求此圆锥侧面展开图的圆心角21在国家的宏观调控下，某市的商品房成交价由去年 10 月份的 14000 元/m 2 下降到 12 月份的11340 元/m 2（1）求 11、12 两月平均每月降价的百分率是多少？（2
6、）如果房价继续回落，按此降价的百分率，你预测到今年 2 月份该市的商品房成交均价是否会跌破 10000 元/m 2？请说明理由22某校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学这餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图（1）这次被调查的同学共有 人；（2）补全条形统计图，并在图上标明相应的数据；（3）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供 50 人食用一餐据此估算，该校 18000 名学生一餐浪费的食物可供多少人食用
7、一餐23如图，在ABC 中，ABAC ，AE 是 BC 边上的高线， BM 平分ABC 交 AE 于点 M，经过B，M 两点的 O 交 BC 于点 G，交 AB 于点 F，FB 为O 的直径（1）求证：AM 是O 的切线；（2）当 BE3，cos C 时，求O 的半径24如图，抛物线 yax 2+bx+c（a0）的顶点为 M，直线 ym 与抛物线交于点 A，B，若AMB为等腰直角三角形，我们把抛物线上 A，B 两点之间的部分与线段 AB 围成的图形称为该抛物线对应的准蝶形，线段 AB 称为碟宽，顶点 M 称为碟顶（1）由定义知，取 AB 中点 N，连结 MN，MN 与 AB 的关系是 （2）抛
8、物线 y 对应的准蝶形必经过 B（m，m），则 m ，对应的碟宽 AB 是 （3）抛物线 yax 24a （a0）对应的碟宽在 x 轴上，且 AB6求抛物线的解析式；在此抛物线的对称轴上是否有这样的点 P（x p，y p），使得APB 为锐角，若有，请求出 yp的取值范围若没有，请说明理由25已知O 的半径为 5，弦 AB 的长度为 m，点 C 是弦 AB 所对优弧上的一动点（1）如图 ，若 m5，则C 的度数为 ；（2）如图 ，若 m6求 C 的正切值；若 ABC 为等腰三角形，求ABC 面积2019 年福建省龙岩市永定县金丰片区中考数学一模试卷参考答案与试题解析一、选择题（每小题 4 分，
9、共 40 分）1下面的图形是天气预报中的图标，其中既是轴对称图形又是中心对称图形的是（ ）A 晴 B 浮尘 C 大雨 D 大雪【分析】根据轴对称图形与中心对称图形的概念求解【解答】解：A、是轴对称图形，也是中心对称图形，故此选项正确；B、是轴对称图形，不是中心对称图形，故此选项错误；C、不是轴对称图形，也不是中心对称图形，故此选项错误；D、不是轴对称图形，也不是中心对称图形，故此选项错误故选：A【点评】本题考查了中心对称图形与轴对称图形的概念：轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合；中心对称图形是要寻找对称中心，旋转 180 度后与原图重合22017 年北京市在经济发展、
10、社会进步、城市建设、民生改善等方面取得新成绩、新面貌综合实力稳步提升全市地区生产总值达到 280000 亿元，将 280000 用科学记数法表示为（ ）A28010 3 B2810 4 C2.810 5 D0.2810 6【分析】科学记数法的表示形式为 a10n 的形式，其中 1|a| 10，n 为整数确定 n 的值时，要看把原数变成 a 时，小数点移动了多少位，n 的绝对值与小数点移动的位数相同当原数绝对值1 时，n 是正数；当原数的绝对值1 时，n 是负数【解答】解：将 280000 用科学记数法表示为 2.8105故选：C【点评】此题考查科学记数法的表示方法科学记数法的表示形式为 a10
11、n 的形式，其中1|a| 10，n 为整数，表示时关键要正确确定 a 的值以及 n 的值3下列计算正确的是（ ）Ax 23x 22x 4 B（3x 2） 26x 2Cx 2y2x32x 6y D6x 3y2（3x）2x 2y2【分析】根据合并同类项法则、积的乘方与幂的乘方、单项式的乘除法逐一计算可得【解答】解：A、x 23x 2 2x2，此选项错误；B、（3x 2） 29x 4，此选项错误；C、x 2y2x32x 5y，此选项错误；D、6x 3y2（3x）2x 2y2，此选项正确；故选：D【点评】本题主要考查整式的运算，解题的关键是掌握合并同类项法则、积的乘方与幂的乘方、单项式的乘除法法则4如
12、图，ABCD，DBBC，250，则1 的度数是（ ）A40 B50 C60 D140【分析】根据直角三角形两锐角互余求出3，再根据两直线平行，同位角相等解答【解答】解：DBBC，250，3902905040，ABCD，1340故选：A【点评】本题考查了平行线的性质，直角三角形两锐角互余的性质，熟记性质是解题的关键5一次函数 yx 2 的图象经过点（ ）A（2，0） B（0，0） C（0，2） D（0，2）【分析】分别把 x0，y 0 代入解析式 yx2 即可求得对应的 y，x 的值【解答】解：当 x0 时，y 2；当 y0 时，x2，因此一次函数 yx 2 的图象经过点（0，2）、（2，0）故
13、选：D【点评】此题考查一次函数图象上点的坐标特征，在这条直线上的各点的坐标一定适合这条直线的解析式6如图，在 RtABC 中，ACB90，CD 是 AB 边上的中线，AC8，BC6，则ACD 的正切值是（ ）A B C D【分析】根据直角三角形斜边上的中线等于斜边的一半可得 CDAD，再根据等边对等角的性质可得AACD，然后根据正切函数的定义列式求出A 的正切值，即为 tanACD 的值【解答】解：CD 是 AB 边上的中线，CDAD，AACD，ACB90，BC6，AC 8，tanA ，tanACD 的值 故选：D【点评】本题考查了锐角三角函数的定义，直角三角形斜边上的中线等于斜边的一半的性质
14、，等边对等角的性质，求出AACD 是解本题的关键7在ABC 中，已知A、B 都是锐角，|sin A |+（ 1tanB） 20，那么C 的度数为（ ）A75 B90 C105 D120【分析】直接利用绝对值的性质以及偶次方的性质得出 sinA ，tanB1，进而得出A30，B45，即可得出答案【解答】解：|sin A |+（1tanB） 20，|sinA |0，（1tanB） 20，sinA ，tanB1，A30，B45，C 的度数为：18030 45105故选：C【点评】此题主要考查了特殊角的三角函数值以及偶次方的性质，正确得出 sinA ，tanB1是解题关键8一个布袋内只装有 1 个黑球
15、和 2 个白球，这些球除颜色外其余都相同，随机摸出一个球后放回并搅匀，再随机摸出一个球，则两次摸出的球都是黑球的概率是（ ）A B C D【分析】列表将所有等可能的结果列举出来，利用概率公式求解即可【解答】解：列表得：黑 白 白黑 （黑，黑） （黑，白） （黑，白）白 （黑，白） （白，白） （白，白）白 （黑，白） （白，白） （白，白）共 9 种等可能的结果，两次都是黑色的情况有 1 种，两次摸出的球都是黑球的概率为 ，故选：D【点评】本题考查了列表法与树状图法的知识，解决本题时采用了两个独立事件同时发生的概率等于两个独立事件单独发生的概率的积，难度不大9如图，P 为平行四边形 ABCD
16、边 AD 上一点，E、F 分别为 PB、PC 的中点，PEF、PDC、PAB 的面积分别为 S、S 1、S 2，若 S2，则 S1+S2（ ）A4 B6 C8 D不能确定【分析】过 P 作 PQ 平行于 DC，由 DC 与 AB 平行，得到 PQ 平行于 AB，可得出四边形 PQCD与 ABQP 都为平行四边形，进而确定出PDC 与PCQ 面积相等，PQB 与ABP 面积相等，再由 EF 为BPC 的中位线，利用中位线定理得到 EF 为 BC 的一半，且 EF 平行于 BC，得出PEF 与 PBC 相似，相似比为 1：2，面积之比为 1：4，求出 PBC 的面积，而PBC 面积CPQ 面积+P
17、BQ 面积，即为PDC 面积+PAB 面积，即为平行四边形面积的一半，即可求出所求的面积【解答】解：过 P 作 PQDC 交 BC 于点 Q，由 DCAB ，得到 PQAB，四边形 PQCD 与四边形 APQB 都为平行四边形，PDCCQP，ABPQPB，S PDC S CQP ，S ABP S QPB ，EF 为PCB 的中位线，EFBC，EF BC，PEF PBC，且相似比为 1：2，S PEF ：S PBC 1：4，S PEF 2，S PBC S CQP +SQPB S PDC +SABP S 1+S28故选：C【点评】此题考查了平行四边形的性质，相似三角形的判定与性质，熟练掌握平行四边
18、形的判定与性质是解本题的关键10如图，ABC 中，ACB90，AB10，tan A 点 P 是斜边 AB 上一个动点过点 P 作PQAB，垂足为 P，交边 AC（或边 CB）于点 Q，设 APx，APQ 的面积为 y，则 y 与 x 之间的函数图象大致为（ ）A BC D【分析】分点 Q 在 AC 上和 BC 上两种情况进行讨论即可【解答】解：当点 Q 在 AC 上时，tanA ，AP x ，PQ x，y APPQ x x x2；当点 Q 在 BC 上时，如下图所示：APx，AB 10，tan A ，BP10x，PQ2BP202x，y APPQ x（202x）x 2+10x，该函数图象前半部分
19、是抛物线开口向上，后半部分也为抛物线开口向下并且当 Q 点在 C 时，x8，y16故选：B【点评】本题考查动点问题的函数图象，有一定难度，解题关键是注意点 Q 在 BC 上这种情况二填空题（每小题 4 分，共 24 分）113 的算术平方根是 【分析】根据开平方的意义，可得算术平方根【解答】解：3 的算术平方根是 ，故答案为： 【点评】本题考查了算术平方根，注意一个正数的算术平方根只有一个12分解因式：x 32x 2+x x（x1） 2 【分析】首先提取公因式 x，进而利用完全平方公式分解因式即可【解答】解：x 32x 2+xx（x 22x+1）x（x 1） 2故答案为：x（x 1） 2【点评
20、】此题主要考查了提取公因式法以及公式法分解因式，熟练应用完全平方公式是解题关键13如图，等边OAB 的边长为 2，则点 B 的坐标为 （1， ） 【分析】过 B 作 BDOA 于 D，则BDO 90，根据等边三角形性质求出 OD，根据勾股定理求出 BD，即可得出答案【解答】解：过 B 作 BDOA 于 D，则BDO 90，OAB 是等边三角形，ODAD OA 1，在 Rt BDO 中，由勾股定理得：BD ，点 B 的坐标为（1， ），故答案为：（1， ）【点评】本题考查了等边三角形的性质，坐标与图形性质和勾股定理等知识点，能正确作出辅助线是解此题的关键14九章算术中记载：“今有牛五、羊二，直金
21、十两；牛二、羊五，直金八两问牛、羊各直金几何？”译文：“假设有 5 头牛、2 只羊，值金 10 两；2 头牛、5 只羊，值金 8 两问每头牛、每只羊各值金多少两？”设每头牛值金 x 两，每只羊值金 y 两，可列方程组为 【分析】根据“假设有 5 头牛、2 只羊，值金 10 两；2 头牛、5 只羊，值金 8 两”，得到等量关系，即可列出方程组【解答】解：根据题意得： 故答案为： 【点评】本题考查了由实际问题抽象出二元一次方程组，解决本题的关键是找到题目中所存在的等量关系15如图，一等腰三角形，底边长是 18 厘米，底边上的高是 18 厘米，现在沿底边依次从下往上画宽度均为 3 厘米的矩形，画出的
22、矩形是正方形时停止，则这个矩形是第 5 个【分析】根据相似三角形的相似比求得顶点到这个正方形的长，再根据矩形的宽求得是第几张【解答】解：已知剪得的纸条中有一张是正方形，则正方形中平行于底边的边是 3，所以根据相似三角形的性质可设从顶点到这个正方形的线段为 x，则 ，解得 x3，所以另一段长为 18315，因为 1535，所以是第 5 张故答案为：5【点评】本题主要考查了相相似三角形的判定和性质，关键是根据似三角形的性质及等腰三角形的性质的综合运用解答16如图，已知在 RtABC 中，ABAC 3 ，在ABC 内作第一个内接正方形 DEFG；然后取GF 的中点 P，连接 PD、PE ，在PDE
23、内作第二个内接正方形 HIKJ；再取线段 KJ 的中点 Q，在QHI 内作第三个内接正方形依次进行下去，则第 2014 个内接正方形的边长为 【分析】首先根据勾股定理得出 BC 的长，进而利用等腰直角三角形的性质得出 DE 的长，再利用锐角三角函数的关系得出 ，即可得出正方形边长之间的变化规律，得出答案即可【解答】解：在 RtABC 中，ABAC ，BC45，BC ，在ABC 内作第一个内接正方形 DEFG；EFECDG BD ，DE BCDE2，取 GF 的中点 P，连接 PD、PE ，在PDE 内作第二个内接正方形 HIKJ；再取线段 KJ 的中点Q，在QHI 内作第三个内接正方形依次进行
24、下去， ，EI KI HI，DHEI，HI DE ，则第 n 个内接正方形的边长为：2 ，则第 2014 个内接正方形的边长为 2 2 故答案为： 【点评】此题主要考查了正方形的性质以及数字变化规律和勾股定理等知识，根据已知得出正方形边长的变化规律是解题关键三解答题（共 9 小题）17解不等式组： ，并把解集在数轴上表示出来【分析】分别求出每一个不等式的解集，根据口诀：同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集【解答】解：解不等式 3（x2）x4，得：x 1，解不等式 x1，得：x4，则不等式组的解集为 1x4，将解集表示在数轴上如下：【点评】本题考查的是解一元一次不
25、等式组，正确求出每一个不等式解集是基础，熟知“同大取大；同小取小；大小小大中间找；大大小小找不到”的原则是解答此题的关键18先化简，再求值：（2 ） ，其中 x2【分析】根据分式的减法和除法可以化简题目中的式子，然后将 x 的值代入化简后的式子即可解答本题【解答】解：（2 ） ，当 x2 时，原式 【点评】本题考查分式的混合运算，解答本题的关键是明确分式混合运算的计算方法19如图，在等边三角形 ABC 中，点 D，E 分别在 BC，AB 上，且ADE60求证：ADCDEB【分析】依据ABC 是等边三角形，即可得到BC60，再根据CADBDE，即可判定ADCDEB【解答】证明：ABC 是等边三角
26、形，BC60，ADBCAD+CCAD +60，ADE60，ADBBDE+60 ，CADBDE，ADCDEB【点评】此题考查了相似三角形的判定与性质、等边三角形的性质等知识解题时注意：有两组角对应相等的两个三角形相似20已知圆锥的底面半径为 3，母线长为 6，求此圆锥侧面展开图的圆心角【分析】易得圆锥的底面周长，就是圆锥的侧面展开图的弧长，利用弧长公式可得圆锥侧面展开图的角度，把相关数值代入即可求解【解答】解：圆锥底面半径是 3，圆锥的底面周长为 6，设圆锥的侧面展开的扇形圆心角为 n，6，解得 n180，答：此圆锥侧面展开图的圆心角是 180【点评】考查了圆锥的计算，用到的知识点为：圆锥的侧面
27、展开图的弧长等于圆锥的底面周长21在国家的宏观调控下，某市的商品房成交价由去年 10 月份的 14000 元/m 2 下降到 12 月份的11340 元/m 2（1）求 11、12 两月平均每月降价的百分率是多少？（2）如果房价继续回落，按此降价的百分率，你预测到今年 2 月份该市的商品房成交均价是否会跌破 10000 元/m 2？请说明理由【分析】（1）设 11、12 两月平均每月降价的百分率是 x，那么 4 月份的房价为 14000（1x），12 月份的房价为 14000（1x） 2，然后根据 12 月份的 11340 元/m 2 即可列出方程解决问题；（2）根据（1）的结果可以计算出今年
28、 2 月份商品房成交均价，然后和 10000 元/m 2 进行比较即可作出判断【解答】解：（1）设 11、12 两月平均每月降价的百分率是 x，则 11 月份的成交价是：14000（1x），12 月份的成交价是：14000（1x） 214000（1x） 211340，（1x） 20.81，x 10.110%，x 21.9（不合题意，舍去）答：11、12 两月平均每月降价的百分率是 10%；（2）会跌破 10000 元/m 2如果按此降价的百分率继续回落，估计今年 2 月份该市的商品房成交均价为：11340（1x） 2113400.819185.410000由此可知今年 2 月份该市的商品房成交
29、均价会跌破 10000 元/m 2【点评】此题考查了一元二次方程的应用，和实际生活结合比较紧密，正确理解题意，找到关键的数量关系，然后列出方程是解题的关键22某校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学这餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图（1）这次被调查的同学共有 1000 人；（2）补全条形统计图，并在图上标明相应的数据；（3）校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供 50 人食用一餐据此估算，该校 1800
30、0 名学生一餐浪费的食物可供多少人食用一餐【分析】（1）用不剩的人数除以其所占的百分比即可；（2）用抽查的总人数减去其他三类的人数，再画出图形即可；（3）根据这次被调查的所有学生一餐浪费的食物可以供 50 人用一餐，再根据全校的总人数是18000 人，列式计算即可【解答】解：（1）这次被调查的学生共有 60060%1000 人，故答案为：1000；（2）剩少量的人数为 1000（600+150+50）200 人，补全条形图如下：（3） ，答：估计该校 18000 名学生一餐浪费的食物可供 900 人食用一餐【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必
31、要的信息是解决问题的关键条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小23如图，在ABC 中，ABAC ，AE 是 BC 边上的高线， BM 平分ABC 交 AE 于点 M，经过B，M 两点的 O 交 BC 于点 G，交 AB 于点 F，FB 为O 的直径（1）求证：AM 是O 的切线；（2）当 BE3，cos C 时，求O 的半径【分析】（1）连结 OM，易证 OMBC ，由于 AE 是 BC 边上的高线，从而可知 AMOM ，所以 AM 是O 的切线（2）由于 ABAC，从而可知 ECBE3，由 cosC ，可知：AC EC ，易证AOMABE，所以 ，再
32、证明 cosAOMcosC ，所以 AO ，从而可求出OM【解答】解：（1）连结 OMBM 平分ABC12 又 OMOB23OM BC AE 是 BC 边上的高线AEBC，AMOMAM 是O 的切线（2）ABACABCC，AEBC，E 是 BC 中点ECBE3cosC AC ECOM BC，AOMABEAOMABE又ABCCAOMC在 Rt AOM 中cosAOM cosC ，AOAB +OB而 ABAC OM O 的半径是【点评】本题考查圆的综合问题，涉及锐角三角函数，相似三角形的判定与性质，等腰三角形的性质等知识，综合程度较高，需要学生综合运用知识的能力24如图，抛物线 yax 2+bx+
33、c（a0）的顶点为 M，直线 ym 与抛物线交于点 A，B，若AMB为等腰直角三角形，我们把抛物线上 A，B 两点之间的部分与线段 AB 围成的图形称为该抛物线对应的准蝶形，线段 AB 称为碟宽，顶点 M 称为碟顶（1）由定义知，取 AB 中点 N，连结 MN，MN 与 AB 的关系是 MNAB，MN AB （2）抛物线 y 对应的准蝶形必经过 B（m，m），则 m 2 ，对应的碟宽 AB 是 4 （3）抛物线 yax 24a （a0）对应的碟宽在 x 轴上，且 AB6求抛物线的解析式；在此抛物线的对称轴上是否有这样的点 P（x p，y p），使得APB 为锐角，若有，请求出 yp的取值范围若
34、没有，请说明理由【分析】（1）直接利用等腰直角三角形的性质分析得出答案；（2）利用已知点为 B（m，m），代入抛物线解析式进而得出 m 的值，即可得出 AB 的值；（3） 根据题意得出抛物线必过（3，0），进而代入求出答案；根据 y x23 的对称轴上 P（0，3），P（0，3）时， APB 为直角，进而得出答案【解答】解：（1）MN 与 AB 的关系是：MNAB，MN AB，如图 1，AMB 是等腰直角三角形，且 N 为 AB 的中点，MNAB，MN AB，故答案为：MNAB，MN AB；（2）抛物线 y 对应的准蝶形必经过 B（m，m），m m2，解得：m2 或 m0（不合题意舍去），当
35、m2 则，2 x2，解得：x2，则 AB2+24；故答案为：2，4；（3） 由已知，抛物线对称轴为：y 轴，抛物线 yax 24a （a 0）对应的碟宽在 x 轴上，且 AB6抛物线必过（3，0），代入 yax 24a （a0），得，9a4a 0，解得：a ，抛物线的解析式是：y x23；由知，如图 2，y x23 的对称轴上 P（0，3），P（0，3）时，APB 为直角，在此抛物线的对称轴上有这样的点 P，使得APB 为锐角，y p 的取值范围是 yp3 或yp3【点评】此题主要考查了二次函数综合以及等腰直角三角形的性质，正确应用等腰直角三角形的性质是解题关键25已知O 的半径为 5，弦 A
36、B 的长度为 m，点 C 是弦 AB 所对优弧上的一动点（1）如图 ，若 m5，则C 的度数为 30 ；（2）如图 ，若 m6求 C 的正切值；若 ABC 为等腰三角形，求ABC 面积【分析】（1）连接 OA，OB，判断出AOB 是等边三角形，即可得出结论；（2） 先求出 AD10，再用勾股定理求出 BD8，进而求出 tanADB，即可得出结论；分三种情况，利用等腰三角形的性质和垂径定理以及勾股定理即可得出结论【解答】解（1）如图 1，连接 OB，OA ，OBOC5，ABm5，OBOCAB，AOB 是等边三角形，AOB60，ACB AOB 30，故答案为 30；（2） 如图 2，连接 AO 并
37、延长交 O 于 D，连接 BD，AD 为 O 的直径，AD10，ABD90，在 Rt ABD 中，AB m6，根据勾股定理得，BD8，tanADB ，CADB ，C 的正切值为 ；、当 ACBC 时，如图 3，连接 CO 并延长交 AB 于 E，ACBC，AOBO，CE 为 AB 的垂直平分线，AEBE3，在 Rt AEO 中，OA5，根据勾股定理得，OE4，CEOE+ OC9，S ABC ABCE 6927；、当 ACAB6 时，如图 4，连接 OA 交 BC 于 F，ACAB，OCOB，AO 是 BC 的垂直平分线，过点 O 作 OGAB 于 G，AOG AOB ，AG AB3，AOB2ACB ，ACFAOG，在 Rt AOG 中，sinAOG ，sinACF ，在 Rt ACF 中，sinACF ，AF AC ，CF ，S ABC AFBC ；、当 BABC 6 时，如图 5，由对称性知，S ABC 【点评】此题是圆的综合题，主要圆的性质，圆周角定理，垂径定理，等腰三角形的性质，三角形的面积公式，用分类讨论的思想解决问题是解本题的关键
