1、2019 年四川省巴中市平昌县中考数学一模试卷一选择题（共 10 小题，满分 30 分，每小题 3 分）1下列关系一定成立的是（ ）A若|a |b|，则 ab B若|a|b，则 abC若|a|b，则 ab D若 a b，则|a| b|2下列运算正确的是（ ）A（2a 3） 24a 5 B 2Cm 2m3m 6 Dx 32x 3x 33中国倡导的“一带一路”建设将促进我国与世界各国的互利合作，根据规划“一带一路”地区覆盖总人口 44 亿，这个数用科学记数法表示为（ ）A4410 8 B4.410 9 C4.410 8 D4.410 104下列所给的汽车标志图案中，既是轴对称图形，又是中心对称图形
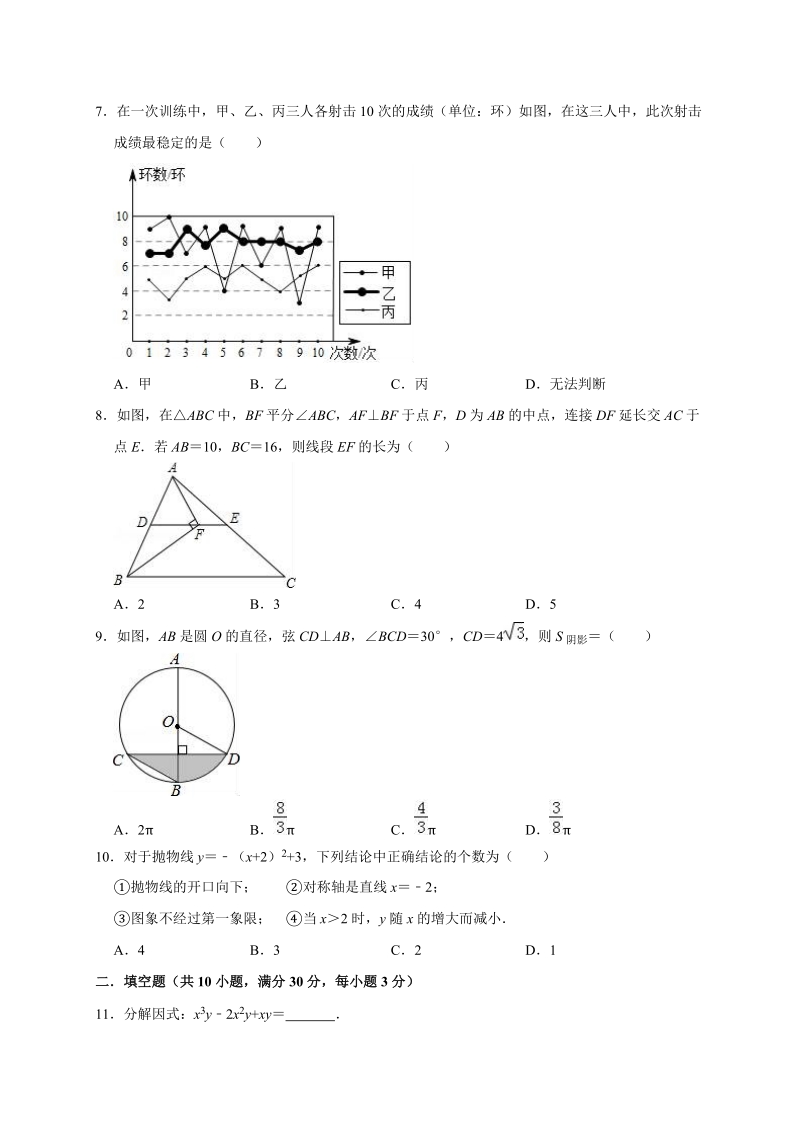
2、的是（ ）A BC D5把不等式组 中每个不等式的解集在同一条数轴上表示出来，正确的为（ ）A BC D6如图，在ABC 中，AB AC ，AB 的垂直平分线交边 AB 于 D 点，交边 AC 于 E 点，若ABC与EBC 的周长分别是 40， 24，则 AB 为（ ）A8 B12 C16 D207在一次训练中，甲、乙、丙三人各射击 10 次的成绩（单位：环）如图，在这三人中，此次射击成绩最稳定的是（ ）A甲 B乙 C丙 D无法判断8如图，在ABC 中，BF 平分ABC ，AF BF 于点 F，D 为 AB 的中点，连接 DF 延长交 AC 于点 E若 AB10，BC16，则线段 EF 的长为
3、（ ）A2 B3 C4 D59如图，AB 是圆 O 的直径，弦 CDAB，BCD30，CD4 ，则 S 阴影 （ ）A2 B C D 10对于抛物线 y（x +2） 2+3，下列结论中正确结论的个数为（ ）抛物线的开口向下； 对称轴是直线 x2；图象不经过第一象限； 当 x2 时，y 随 x 的增大而减小A4 B3 C2 D1二填空题（共 10 小题，满分 30 分，每小题 3 分）11分解因式：x 3y2x 2y+xy 12如图，已知 ab，小亮把三角板的直角顶点放在直线 b 上若135，则2 的度数为 13若代数式 有意义，则 m 的取值范围是 14如果一个正多边形每一个内角都等于 144
4、，那么这个正多边形的边数是 15如图，长方形 ABCD 中，AB4cm，BC 3cm ，E 为 CD 的中点动点 P 从 A 点出发，以每秒1cm 的速度沿 ABCE 运动，最终到达点 E若点 P 运动的时间为 x 秒，则当 x 时，APE 的面积等于 516如图，在等边ABC 内有一点 D，AD5，BD 6， CD4，将ABD 绕 A 点逆时针旋转，使 AB 与 AC 重合，点 D 旋转至点 E，过 E 点作 EHCD 于 H，则 EH 的长为 17若反比例函数 y （k 0）的图象经过点（1，3 ），则一次函数 ykxk（k0）的图象经过 象限18已知 x1，x 2 是方程 x23 x+1
5、0 的两个实数根，则 19如图，直线 ，点 A1 坐标为（1，0），过点 A1 作 x 轴的垂线交直线于点 B1，以原点 O为圆心，OB 1 长为半径画弧交 x 轴于点 A2；再过点 A2 作 x 轴的垂线交直线于点 B2，以原点 O为圆心，OB 2 长为半径画弧交 x 轴于点 A3，按此做法进行下去，点 An 的坐标为 20如图，AB 是O 的直径，且经过弦 CD 的中点 H，过 CD 延长线上一点 E 作O 的切线，切点为 F，若 ACF64，则 E 三解答题（共 11 小题，满分 90 分）21（6 分）计算：22（6 分）如图，一个长方形运动场被分隔成 A、B、A、B、C 共 5 个区
6、，A 区是边长为 am 的正方形，C 区是边长为 bm 的正方形（1）列式表示每个 B 区长方形场地的周长，并将式子化简；（2）列式表示整个长方形运动场的周长，并将式子化简；（3）如果 a20，b10，求整个长方形运动场的面积23（6 分）定义新运算：对于任意实数 m，n 都有 m nm 2n+n，等式右边是常用的加法、减法、乘法及乘方运算例如：32（3） 22+220根据以上知识解决问题：若 2a 的值小于 0（1）求 a 的值；（2）请判断方程：2x 2bx +a0 的根的情况24（6 分）如图，四边形 ABCD 是菱形，CEAB 交 AB 的延长线于点 E，CFAD 交 AD 的延长线于
7、点 F，求证：DFBE 25（10 分）济南某中学在参加“创文明城，点赞泉城”书画比赛中，杨老师从全校 30 个班中随机抽取了 4 个班（用 A，B，C ，D 表示），对征集到的作鼎的数量进行了分析统计，制作了两幅不完整的统计图请根据以上信息，回答下列问题：（l）杨老师采用的调查方式是 （填“普查”或“抽样调查”）；（2）请补充完整条形统计图，并计算扇形统计图中 C 班作品数量所对应的圆心角度数 （3）请估计全校共征集作品的什数（4）如果全枝征集的作品中有 5 件获得一等奖，其中有 3 名作者是男生，2 名作者是女生，现要在获得一样等奖的作者中选取两人参加表彰座谈会，请你用列表或树状图的方法，
8、求恰好选取的两名学生性别相同的概率26（6 分）如图，在平面直角坐标系中，AOB 的三个顶点坐标分别为 A（1，0），O（0，0），B（2， 2）以点 O 为旋转中心，将 AOB 逆时针旋转 90，得到A 1OB1（1）画出A 1OB1；（2）直接写出点 A1 和点 B1 的坐标；（3）求线段 OB1 的长度27（10 分）整顿药品市场、降低药品价格是国家的惠民政策之一根据国家药品政府定价办法，某省有关部门规定：市场流通药品的零售价格不得超过进价的 15%根据相关信息解决下列问题：（1）降价前，甲乙两种药品每盒的出厂价格之和为 6.6 元经过若干中间环节，甲种药品每盒的零售价格比出厂价格的 5
9、 倍少 2.2 元，乙种药品每盒的零售价格是出厂价格的 6 倍，两种药品每盒的零售价格之和为 33.8 元那么降价前甲、乙两种药品每盒的零售价格分别是多少元？（2）降价后，某药品经销商将上述的甲、乙两种药品分别以每盒 8 元和 5 元的价格销售给医院，医院根据实际情况决定：对甲种药品每盒加价 15%、对乙种药品每盒加价 10%后零售给患者实际进药时，这两种药品均以每 10 盒为 1 箱进行包装近期该医院准备从经销商处购进甲乙两种药品共 100 箱，其中乙种药品不少于 40 箱，销售这批药品的总利润不低于 900 元请问购进时有哪几种搭配方案？28（10 分）如图，在平面直角坐标系 xOy 中，
10、已知正比例函数 y12x 的图象与反比例函数y2 的图象交于 A（1 ，n），B 两点（1）求出反比例函数的解析式及点 B 的坐标；（2）观察图象，请直接写出满足 y2 的取值范围；（3）点 P 是第四象限内反比例函数的图象上一点，若POB 的面积为 1，请直接写出点 P 的横坐标29（8 分）如图，在一条河的北岸有两个目标 M、N，现在位于它的对岸设定两个观测点A、B 已知 ABMN，在 A 点测得MAB 60，在 B 点测得MBA 45，AB600 米 （1）求点 M 到 AB 的距离；（结果保留根号）（2）在 B 点又测得NBA53，求 MN 的长（结果精确到 1 米）（参考数据： 1.
11、732，sin530.8，cos530.6，tan531.33，cot53 0.75）30（10 分）如图，已知以 RtABC 的边 AB 为直径作 ABC 的外接圆 O，B 的平分线 BE 交AC 于 D，交O 于 E，过 E 作 EFAC 交 BA 的延长线于 F（1）求证：EF 是O 切线；（2）若 AB15，EF 10，求 AE 的长31（12 分）如图 1，抛物线 yax 2+bx+3 交 x 轴于点 A（1，0）和点 B（3，0）（1）求该抛物线所对应的函数解析式；（2）如图 2，该抛物线与 y 轴交于点 C，顶点为 F，点 D（2，3）在该抛物线上求四边形 ACFD 的面积；点
12、P 是线段 AB 上的动点（点 P 不与点 A、B 重合），过点 P 作 PQx 轴交该抛物线于点Q，连接 AQ、DQ，当AQD 是直角三角形时，求出所有满足条件的点 Q 的坐标2019 年四川省巴中市平昌县中考数学一模试卷参考答案与试题解析一选择题（共 10 小题，满分 30 分，每小题 3 分）1【分析】根据绝对值的定义进行分析即可得出正确结论【解答】解：选项 A、B、C 中，a 与 b 的关系还有可能互为相反数故选 D【点评】绝对值相等的两个数的关系是相等或互为相反数2【分析】根据整式的运算法则即可求出答案【解答】解：（A）原式4a 6，故 A 不正确；（B）原式2，故 B 不正确；（C
13、）原式m 5，故 C 不正确；故选：D【点评】本题考查学生的计算能力，解题的关键是熟练运用整式的运算法则，本题属于基础题型3【分析】用科学记数法表示较大的数时，一般形式为 a10n，其中 1|a| 10，n 为整数，据此判断即可【解答】解：44 亿4.410 9故选：B【点评】此题主要考查了用科学记数法表示较大的数，一般形式为 a10n，其中 1|a| 10，确定 a 与 n 的值是解题的关键4【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解【解答】解：A、是轴对称图形，不是中心对称图形，故本选项错误；B、既是轴对称图形，又是中心对称图形，故本选项正确；C、是轴对称图形，不是
14、中心对称图形，故本选项错误；D、是轴对称图形，不是中心对称图形，故本选项错误故选：B【点评】本题考查了中心对称图形与轴对称图形的概念轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转 180 度后两部分重合5【分析】先求出不等式组中各个不等式的解集，再利用数轴确定不等式组的解集【解答】解：解不等式 x+13，得：x2，解不等式2x64，得：x1，将两不等式解集表示在数轴上如下：故选：B【点评】本题考查了解一元一次不等式组，在数轴上表示不等式的解集解不等式组时要注意解集的确定原则：同大取大，同小取小，大小小大取中间，大大小小无解了6【分析】首先根据 DE 是
15、 AB 的垂直平分线，可得 AEBE ；然后根据ABC 的周长AB +AC+BC，EBC 的周长BE +EC+BCAE+EC +BCAC+BC ，可得ABC 的周长EBC 的周长AB ，据此求出 AB 的长度是多少即可【解答】解：DE 是 AB 的垂直平分线，AEBE；ABC 的周长AB +AC+BC，EBC 的周长BE+EC +BCAE+EC+BCAC+ BC，ABC 的周长EBC 的周长AB，AB402416故选：C【点评】此题主要考查了垂直平分线的性质，要熟练掌握，解答此题的关键是要明确：垂直平分线上任意一点，到线段两端点的距离相等此题还考查了等腰三角形的性质，以及三角形的周长的求法，要
16、熟练掌握7【分析】根据方差的定义，方差越小数据越稳定，即可得出答案【解答】解：根据统计图波动情况来看，此次射击成绩最稳定的是乙，波动比较小，比较稳定故选：B【点评】本题考查了方差的意义方差是用来衡量一组数据波动大小的量，方差越大，表明这组数据偏离平均数越大，即波动越大，数据越不稳定；反之，方差越小，表明这组数据分布比较集中，各数据偏离平均数越小，即波动越小，数据越稳定8【分析】根据直角三角形斜边上中线是斜边的一半可得 DF ABADBD5 且ABFBFD ，结合角平分线可得CBFDFB，即 DEBC，进而可得 DE8，由EF DEDF 可得答案【解答】解：AFBF ，AFB 90，AB10，D
17、 为 AB 中点，DF ABADBD 5，ABF BFD，又BF 平分ABC ，ABF CBF，CBFDFB，DEBC，ADEABC， ，即 ，解得：DE8，EFDE DF3，故选：B【点评】本题主要考查直角三角形的性质和相似三角形的判定与性质，熟练运用其判定与性质是解题的关键9【分析】根据垂径定理求得 CEED2 ，然后由圆周角定理知DOE 60，然后通过解直角三角形求得线段 OD、 OE 的长度，最后将相关线段的长度代入 S 阴影 S 扇形 ODBS DOE+SBEC 方法二：直接证明： S 阴影 S 扇形 ODB【解答】解：如图，假设线段 CD、AB 交于点 E，AB 是O 的直径，弦
18、CDAB，CEED2 ，又BCD30，DOE 2 BCD60， ODE 30，OEDE cot602 2，OD2OE4，S 阴影 S 扇形 ODBS DOE +SBEC OEDE+ BECE 2 +2 故选 B方法二：证明CEBDEO（AAS），可得 S 阴影 S 扇形 ODB【点评】考查了垂径定理、扇形面积的计算，通过解直角三角形得到相关线段的长度是解答本题的关键10【分析】根据抛物线的解析式可求得其开口方向、对称轴，则可判断、，由解析式可求得抛物线的顶点坐标及与 x 轴的交点坐标，则可判断；利用抛物线的对称轴及开口方向可判断；则可求得答案【解答】解：y（x+2） 2+3，抛物线开口向下、对
19、称轴为直线 x2，顶点坐标为（2，3），故、都正确；在 y（x+2） 2+3 中，令 y0 可求得 x2+ 0，或 x2 0，抛物线图象不经过第一象限，故正确；抛物线开口向下，对称轴为 x2，当 x2 时，y 随 x 的增大而减小，当 x2 时，y 随 x 的增大而减小，故 正确；综上可知正确的结论有 4 个，故选：A【点评】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在ya（xh） 2+k 中，对称轴为 xh，顶点坐标为（h，k）二填空题（共 10 小题，满分 30 分，每小题 3 分）11【分析】原式提取公因式，再利用完全平方公式分解即可【解答】解：原式xy（x 22x
20、+1）xy（x1） 2故答案为：xy（x1） 2【点评】此题考查了提公因式法与公式法的综合运用，熟练掌握因式分解的方法是解本题的关键12【分析】根据直角的度数求出3，再根据两直线平行，同位角相等可得2 的度数【解答】解：135，ABC90，390155，ab，2355【点评】本题考查了平行线的性质，直角三角形的性质，熟记性质并准确识图是解题的关键13【分析】根据二次根式有意义的条件可得 m+10，根据分式有意义的条件可得 m10，再解即可【解答】解：由题意得：m+10，且 m10，解得：m1，且 m1，故答案为：m1，且 m1【点评】此题主要考查了分式和二次根式有意义的条件，关键是掌握：分式有
21、意义，分母不为0；二次根式的被开方数是非负数14【分析】设正多边形的边数为 n，然后根据多边形的内角和公式列方程求解即可【解答】解：设正多边形的边数为 n，由题意得， 144，解得 n10故答案为：10【点评】本题考查了多边形的内角与外角，熟记公式并准确列出方程是解题的关键15【分析】分 P 在 AB 上、P 在 BC 上、P 在 CE 上三种情况，根据三角形的面积公式计算即可【解答】解：当 P 在 AB 上时，APE 的面积等于 5， x35，x ；当 P 在 BC 上时，APE 的面积等于 5，S 矩形 ABCDS CPE S ADE S ABP 5，34 （3+4x）2 23 4（x 4
22、） 5，x5；当 P 在 CE 上时，（4+3+2x）35，x （不合题意），故答案为： 或 5【点评】本题考查的是三角形的面积计算，灵活运用分情况讨论思想是解题的关键16【分析】先利用等边三角形的性质得到BAC60，ABAC，再利用旋转的性质得DAE BAC60，AD AE 5，CEBD6，则可判断ADE 为等边三角形得到DEAD5，设 DHx，则 CHCDDH4x ，于是根据勾股定理得到EH2+x25 2，EH 2+（4x ） 26 2，然后利用加减消元法先求出 x，再计算 EH 即可【解答】解：ABC 为等边三角形，BAC60，AB AC，将ABD 绕 A 点逆时针旋转，使 AB 与 A
23、C 重合，点 D 旋转至点 E，DAEBAC60，AD AE 5，CEBD6，ADE 为等边三角形，DEAD 5，设 DHx，则 CHCDDH4x，在 Rt DHE 中，EH 2+x25 2，在 Rt CHE 中， EH2+（4x） 26 2，得 16 8x11，解得 x ，EH 故答案为 【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等也考查了等边三角形的性质17【分析】由题意知，k1（3）30，所以一次函数解析式为 y3x+3，根据 k，b的值判断一次函 ykxk 的图象经过的象限【解答】解：反比例函数 y （k0）的
24、图象经过点（ 1，3），k1（3）30，一次函数解析式为 y3x+3，根据 k、b 的值得出图象经过一、二、四象限故答案为：一、二、四【点评】本题考查了一次函数的性质及利用待定系数法求反比例函数的解析式，其中利用的知识点：（1）用待定系数法确定反比例函数的 k 的值；（2）对于一次函数 ykx +b，如果k0，b0，那么图象经过一、二、四象限18【分析】首先根据根与系数的关系求出 x1+x23，x 1x21，然后将 变形，再将x1+x23，x 1x21 代入即可【解答】解：x 1，x 2 是方程 x23x+10 的两个实数根，根据根与系数的关系有：x 1+x23，x 1x21，所以 3故答案为
25、：3【点评】本题主要考查根与系数的关系，关键是熟练运用19【分析】先根据一次函数方程式求出 B1 点的坐标，在根据 B1 点的坐标求出 A2 点的坐标，以此类推总结规律便可求出点 An 的坐标【解答】解：直线 y x，点 A1 坐标为（1，0），过点 A1 作 x 轴的垂线交 直线于点 B1 可知B1 点的坐标为（1， ），以原 O 为圆心，OB 1 长为半径画弧 x 轴于点 A2，OA 2OB 1，OA2 2，点 A2 的坐标为（2，0），这种方法可求得 B2 的坐标为（2，2 ），故点 A3 的坐标为（4，0），此类推便可求出点 An 的坐标为（2 n1 ，0）故答案为：（2 n1 ，0）
26、【点评】本题主要考查了一次函数的应用，做题时要注意数形结合思想的运用，是各地的中考热点，学生在平常要多加训练，属于中档题20【分析】连接 OF只要证明 OFEOHE90，利用四边形内角和定理求出AOF 即可解决问题【解答】解：连接 OF，EF 是O 切线，OFEF，AB 是直径，AB 经过 CD 中点 H，OHEH ，又AOF2ACF 128，在四边形 EFOH 中，OFE+OHE 180E180AOF 18012852【点评】本题考查了切线的性质，圆周角定理，垂径定理，正确的作出辅助线是解题的关键三解答题（共 11 小题，满分 90 分）21【分析】原式利用特殊角的三角函数值，负整数指数幂法
27、则，以及绝对值的代数意义计算即可求出值【解答】解：原式3 +4 +1 +5【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键22【分析】（1）根据题意可知 B 的区是长为（a+b）m，宽为（ab）m 的长方形，利用周长公式即可求出答案（2）整个长方形的长为（2a+b）m，宽为（2ab）m ，利用周长公式求出答案即可（3）将 a 与 b 的值代入即长与宽中，利用面积公式即可求出答案【解答】解：（1）2（a+b）+（ab）2（a+b+ ab）4a（m）；（2）2（a+ a+b）+（a+ab） 2（a+a+b+a+ab）8a（m）；（3）当 a20，b10 时，长2a+b50（m），宽2a
28、b30（m），所以面积50301500（m 2）【点评】本题考查代数式求值，涉及长方形面积公式，周长公式，属于基础题型23【分析】（1）根据新运算的定义式结合 2a 的值小于 0，即可得出关于 a 的一元一次不等式，解之即可得出结论；（2）根据方程的系数结合根的判别式，即可得出b 28a8a0，由此可得出方程2x2bx+a0 有两个不相等的实数根【解答】解：（1）2a 的值小于 0，2 2a+a5a0，解得：a0（2）在方程 2x2bx +a0 中，（b） 242ab 28a8a0，方程 2x2bx+a0 有两个不相等的实数根【点评】本题考查了根的判别式以及实数的运算，解题的关键是：（1）根据
29、新运算的定义式找出关于 a 的一元一次不等式；（2）牢记“当0 时，方程有两个不相等的实数根”24【分析】连接 AC，根据菱形的性质可得 AC 平分DAE，CDBC ，再根据角平分线的性质可得 CEFC，然后利用 HL 证明 RtCDFRtCBE，即可得出 DFBE【解答】解：连接 AC，四边形 ABCD 是菱形，AC 平分DAE ，CDBC，CEAB，CFAD ，CEFC，CFDCEB90在 Rt CDF 与 RtCBE 中，RtCDF RtCBE （HL ），DFBE【点评】本题考查菱形的性质，解题的关键是熟练运用全等三角形的判定以及性质，本题属于基础题型25【分析】（1）杨老师从全校 3
30、0 个班中随机抽取了 4 个班，属于抽样调查（2）由题意得：所调查的 4 个班征集到的作品数为：6 24（件），C 班作品的件数为：2446410（件）；继而可补全条形统计图；（3）先求出抽取的 4 个班每班平均征集的数量，再乘以班级总数可得；（4）首先根据题意画出树状图，然后由树状图求得所有等可能的结果与两名学生性别相同的情况，再利用概率公式即可求得答案【解答】解：（1）杨老师从全校 30 个班中随机抽取了 4 个班，属于抽样调查故答案为：抽样调查（2）所调查的 4 个班征集到的作品数为：6 24 件，C 班有 24（4+6+4）10 件，补全条形图如图所示，扇形统计图中 C 班作品数量所对
31、应的圆心角度数 360 150；故答案为：150；（3）平均每个班 6 件，估计全校共征集作品 630180 件（4）画树状图得：共有 20 种等可能的结果，两名学生性别相同的有 8 种情况，恰好选取的两名学生性别相同的概率为 【点评】本题考查的是条形统计图和扇形统计图的综合运用，读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键条形统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小同时考查了概率公式26【分析】（1）分别作出点 A 和点 B 绕点 O 逆时针旋转 90所得对应点，再与点 O 首尾顺次连接即可得；（2）由所得图形可得点的坐标；（3）利用勾股定理
32、可得答案【解答】解：（1）画出A 1OB1，如图（2）点 A1（0，1），点 B1（2，2）（3）OB 1OB 2 【点评】本题主要考查作图旋转变换，解题的关键是掌握旋转变换的定义和性质，并据此得出变换后的对应点27【分析】（1）等量关系为：甲出厂价+乙出厂价6.6；甲零售价+乙零售价33.8；（2）关系式为：甲药品的利润+乙药品的利润900；乙种药品箱数40【解答】解：（1）设甲种药品的出厂价格为每盒 x 元，乙种药品的出厂价格为每盒 y 元则根据题意列方程组得： ，解之得： ，53.62.2182.215.8（元）6318（元），答：降价前甲、乙两种药品每盒的零售价格分别是 15.8 元和
33、 18 元；（2）设购进甲药品 z 箱（z 为非负整数），购进乙药品（100z）箱则根据题意列不等式组得： ，解得：57 z60，则 z 可取：58，59，60，此时 100z 的值分别是：42，41，40；有 3 种方案供选择：第一种方案，甲药品购买 58 箱，乙药品购买 42 箱；第二种方案，甲药品购买 59 箱，乙药品购买 41 箱；第三种方案，甲药品购买 60 箱，乙药品购买 40 箱【点评】找到相应的关系式是解决本题的关键，注意不低于意思是大于或等于；不超过意思是小于或等于28【分析】（1）把 A（1，n）代入 y2x ，可得 A（1，2），把 A（1，2）代入y ，可得反比例函数的
34、表达式为 y ，再根据点 B 与点 A 关于原点对称，即可得到 B 的坐标；（2）观察函数图象即可求解；（3）设 P（m， ），根据 S 梯形 MBPNS POB 1，可得方程 （2+ ）（m1）1 或（2+ ）（1m）1，求得 m 的值，即可得到点 P 的横坐标【解答】解：（1）把 A（1，n）代入 y2x ，可得 n2，A（1，2），把 A（1，2）代入 y ，可得 k2，反比例函数的表达式为 y ，点 B 与点 A 关于原点对称，B（1，2）（2）A（1，2），y2 的取值范围是 x1 或 x0；（3）作 BMx 轴于 M，PN x 轴于 N，S 梯形 MBPN SPOB 1，设 P（m
35、， ），则 （2+ ）（m 1）1 或 （2+ ）（1m ）1整理得，m 2m10 或 m2+m+10，解得 m 或 m ，P 点的横坐标为 【点评】本题主要考查了反比例函数与一次函数的交点问题，解题时注意：反比例函数与一次函数的图象的交点坐标满足两函数的解析式29【分析】（1）过点 M 作 MDAB 于点 D，易求 AD 的长，再由 BDMD 可得 BD 的长，即M 到 AB 的距离；（2）过点 N 作 NEAB 于点 E，易证四边形 MDEN 为平行四边形，所以 ME 的长可求出，再根据 MNABADBE 计算即可【解答】解：（1）过点 M 作 MDAB 于点 D，MD AB，MDAMDB
36、 90，MAB 60 ，MBA 45 ，在 RtADM 中， ；在 Rt BDM 中， ， ，AB600m，AD+ BD600m， ， ， ，点 M 到 AB 的距离 （2）过点 N 作 NEAB 于点 E，MD AB，NE AB，MD NE，ABMN，四边形 MDEN 为平行四边形， ，MNDE ，NBA53，在 RtNEB 中， ， ， 【点评】本题考查了解直角三角形的应用，通过解直角三角形能解决实际问题中的很多有关测量问题，根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形，得到数学问题的答案，再转化得到实际问题的答案是解题的关键30【分析】（1）要证 EF 是 O 的切线，只
37、要连接 OE，再证FEO90即可；（2）证明FEAFBA ，得出 AE，BF 的比例关系式，勾股定理得出 AE，BF 的关系式，求出 AE 的长【解答】（1）证明：连接 OE，B 的平分线 BE 交 AC 于 D，CBEABEEFAC，CAEFEAOBEOEB，CBECAE，FEA OEBAEB 90，FEO90EF 是O 切线（2）解：AFFB EFEF，AF（AF+15）1010AF5FB20FF ，FEAFBE，FEA FBEEF10AE 2+BE21515AE3 【点评】本题考查了切线的判定要证某线是圆的切线，已知此线过圆上某点，连接圆心与这点（即为半径），再证垂直即可31【分析】（1
38、）由 A、B 两点的坐标，利用待定系数法即可求得抛物线解析式；（2） 连接 CD，则可知 CDx 轴，由 A、F 的坐标可知 F、A 到 CD 的距离，利用三角形面积公式可求得ACD 和FCD 的面积，则可求得四边形 ACFD 的面积；由题意可知点 A 处不可能是直角，则有ADQ 90或AQD 90，当 ADQ90时，可先求得直线 AD 解析式，则可求出直线 DQ 解析式，联立直线 DQ 和抛物线解析式则可求得 Q 点坐标；当AQD 90时，设 Q（t， t 2+2t+3），设直线 AQ 的解析式为 yk 1x+b1，则可用 t 表示出k，设直线 DQ 解析式为 yk 2x+b2，同理可表示出
39、 k2，由 AQDQ 则可得到关于 t 的方程，可求得 t 的值，即可求得 Q 点坐标【解答】解：（1）由题意可得 ，解得 ，抛物线解析式为 yx 2+2x+3；（2） yx 2+2x+3（x1） 2+4，F（1，4），C（0，3），D（2，3），CD2，且 CDx 轴，A（1，0），S 四边形 ACFDS ACD +SFCD 23+ 2（4 3）4；点 P 在线段 AB 上，DAQ 不可能为直角，当AQD 为直角三角形时，有ADQ 90或AQD90，i当ADQ 90时，则 DQAD，A（1，0），D（2，3），直线 AD 解析式为 yx+1，可设直线 DQ 解析式为 y x +b，把 D（2
40、，3）代入可求得 b 5，直线 DQ 解析式为 yx +5，联立直线 DQ 和抛物线解析式可得 ，解得 或 ，Q（1，4）；ii当AQD 90时，设 Q（t ，t 2+2t+3），设直线 AQ 的解析式为 yk 1x+b1，把 A、Q 坐标代入可得 ，解得 k1（t3），设直线 DQ 解析式为 yk 2x+b2，同理可求得 k2t，AQDQ ，k 1k21，即 t（t3） 1，解得 t ，当 t 时， t 2+2t+3 ，当 t 时， t 2+2t+3 ，Q 点坐标为（ ， ）或（ ， ）；综上可知 Q 点坐标为（1，4 ）或（ ， ）或（ ， ）【点评】本题为二次函数的综合应用，涉及待定系数法、三角形的面积、二次函数的性质、直角三角形的性质及分类讨论思想等知识在（1）中注意待定系数法的应用，在（2）中注意把四边形转化为两个三角形，在利用互相垂直直线的性质是解题的关键本题考查知识点较多，综合性较强，难度适中
