1、2.5 三元一次方程组及其解法(选学) 知识点 解三元一次方程组基本思路：用代入法或加减法消去一个未知数，化成二元一次方程组，再解这个二元一次方程组点拨 一般步骤：三元(方程组) 二元(方程组) 一元(方程) 消 元 消 元 解方程组： x 2y 9，x y z 7，2x 3y z 12.)探究 一 方程组中每个方程都是三元一次方程的三元一次方程组的解法教材例 1 变式题解方程组：2x 4y 3z 9，3x 2y 4z 8，5x 6y 5z 7.)归纳总结 当三元一次方程组中的每一个方程都是三元一次方程(即每个方程含三个未知数)时，有两种解法解法一(代入法)：首先选择未知数的系数的绝对值较小的
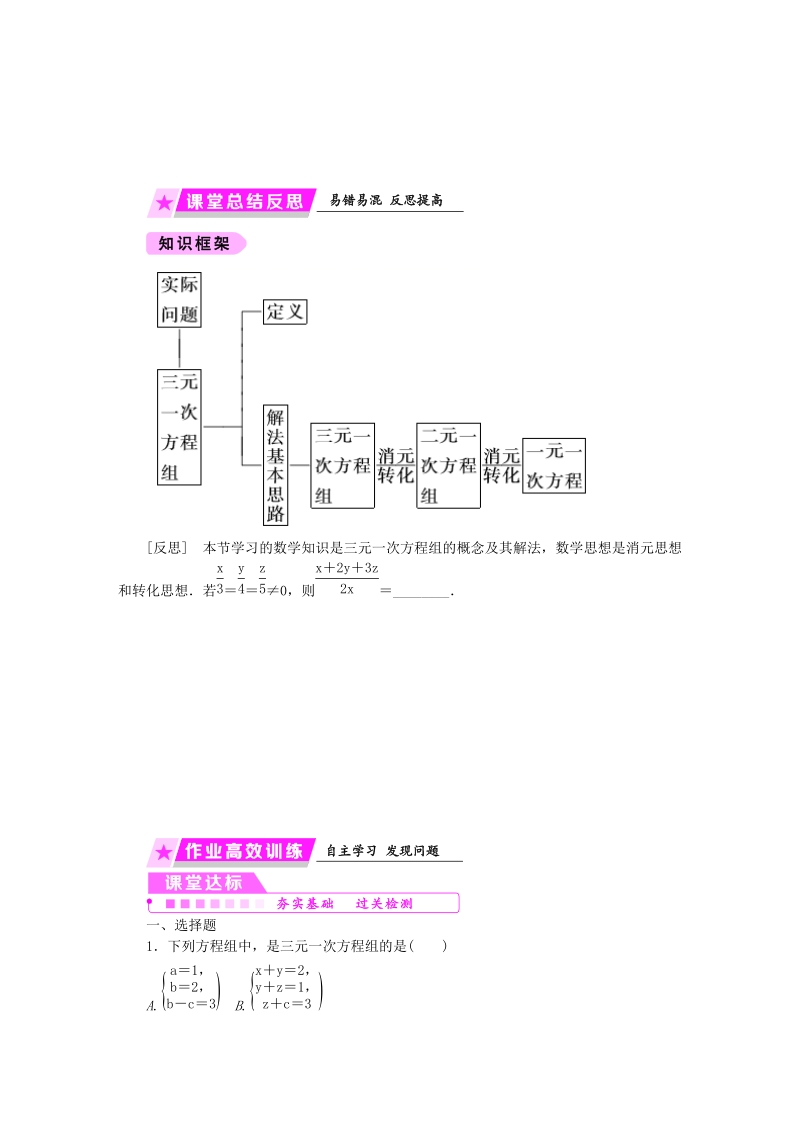
2、方程，在这个方程中，用其他两个未知数表示这个系数绝对值较小的未知数，然后分别代入另外两个方程，得到一个二元一次方程组，并解之；解法二(加减法)：当方程组中相同未知数的系数的绝对值之间存在相等或成整数倍数关系或最小公倍数较小时，就可消去这个未知数，转化为二元一次方程组探究 二 用特殊的方法解三元一次方程组教材补充题解方程组：(1) x y 7，y z 8，z x 9； )(2)x y 3 2，y z 5 4，x y z 66. )反思 本节学习的数学知识是三元一次方程组的概念及其解法，数学思想是消元思想和转化思想若 0，则 _x3 y4 z5 x 2y 3z2x一、选择题1下列方程组中，是三元一
3、次方程组的是( )A. B.a 1，b 2，b c 3) x y 2，y z 1，z c 3)C. D.4x 3y 7，5x 2y 14，2x y 4 ) xy z 3，x yz 5，xz y 7)2解为 的方程组是( )x 1，y 1，z 2)A. B.x y z 4，2x y z 1，3x 2y 4z 3) x y z 0，z y x 1，2x y 2z 5)C. D.x y 4，y z 5，x z 6) 2x 3y z 5，x y z 4，x y 2z 2 )3三元一次方程组 的解是( )x y 1，y z 5，z x 6)A. B.x 1，y 0，z 5) x 1，y 2，z 4)C.
4、 D.x 1，y 0，z 4) x 4，y 1，z 0)4解三元一次方程组： a b c 1， a 2b c 3， 2a 3b 2c 5. )具体过程如下：(1)，得 b2，(2)2，得 4a2b7.(3)所以 b 2，4a 2b 7.)(4)把 b2 代入 4a2b7，得 4a227(以下求解过程略)其中错误的一步是( )A(1) B(2) C(3) D(4)5若 x，y 同时满足下列三个等式：5x2ya，3x2y7a，4xya1，则 a 的值为( )A2 B1 C1 D2二、填空题6已知三元一次方程 2x3y4z8，用含 x，y 的代数式表示 z 是_7若 是关于 x，y，z 的方程 3x
5、2ymz0 的解，则 m_x 1，y 2，z 1 )8已知 则 xyz_x y 5，y z 2，z x 3， )9解三元一次方程组 时，先消去 z，得二元一次方程组_，x 2y z 3，2x y z 5，3x 4y z 10)再消去 y，得一元一次方程_，解得 _，从而得y_，z_三、解答题10解下列方程组：(1)2x y 3z 3，3x y 2z 1，x y z 5； )(2)x3yy2zxz5；(3)2x 3y z 6，x y 2z 1，x 2y z 5. )11若|x2|3x6y|(3yz) 20，求 xyz 的值12某单位职工在植树节当天去植树，甲、乙、丙三个小组共植树 50 棵，乙组
6、植树的棵数是甲、丙两组和的 ，甲组植树的棵数恰好是乙组和丙组的和，问每组各植树多少棵？1413为确保信息安全，信息需加密传输，发送方由明文 密文(加密)，接收方由密文 明文(解密)已知加密规则为明文 x，y，z 对应密文 2x3y，3x4y，3z.例如：明文 1，2，3 对应密文 8，11，9.当接收方收到密文 12，17，27 时，请你求解密得到的明文14若规定 adbc，如 203(1)3.解方程组： 1，|a cb d| |2 -13 0 | |3 y2 x|8，|x z-3 5| 3.|3 z6 y|技巧性题目 已知方程组 的解使代数式 x2y3z 的值等于10，求 ax y 3a，y
7、 z 5a，z x 4a)的值详解详析教材的地位和作用三元一次方程组是代数方程的一种，本节在二元一次方程组解法的基础上，借助类比的方法学习三元一次方程组的解法通过对它的学习，可以了解多元一次方程组的概念和解法，也是后续学习函数、平面解析几何以及物理、化学等运算的工具本考点在中考时单独命题，形式多以解答题为主知识与技能1.了解三元一次方程组及其相关概念；2.掌握解简单的三元一次方程组的方法过程与方法1.通过对方程组中未知数的特点的观察分析，明确解三元一次方程组的主要思想是“消元” ，从而促成未知向已知转化，培养观察能力和体会化归的思想；2.通过代入法、加减法解三元一次方程组及选用合理、简捷的方法
8、解方程组的训练，培养运算能力教学目标情感、态度与价值观通过研究解决问题的方法，培养学生合作交流的意识与探究精神重点 利用消元思想解某些简单的三元一次方程组难点 正确、灵活地选择代入法和加减法解三元一次方程组教学重点难点 易错 点 对用含一个未知数的代数式来表示另一个未知数的变形不熟练，从而导致 解答错误【预习效果检测】解析 中缺少未知数 z，解法一：由得 x2 y9，把x 2y 9， x y z 7， 2x 3y z 12， )x2 y9 分别代入，得到一个关于 y， z 的二元一次方程组；解法二：既然中不含z，那么在和中消去 z 后，得到一个关于 x， y 的方程 3x2 y19 与联立，得
9、到一个关于 x， y 的二元一次方程组解： x 2y 9， x y z 7， 2x 3y z 12， )解法一：由，得 x2 y9.把分别代入，得 3y z 2，y z 6.)解这个方程组，得 y 2，z 4.)把 y2 代入，得 x5.所以原方程组的解为 x 5，y 2，z 4.)解法二：，得 3x2 y19.联立与，得 x 2y 9，3x 2y 19.)解这个方程组，得 x 5，y 2.)把 x5， y2 代入，得 52 z7，所以 z4.所以原方程组的解为 x 5，y 2，z 4.)【重难互动探究】例 1 解析 解法一(用代入法)：方程组中，未知数的系数绝对2x 4y 3z 9， 3x
10、2y 4z 8， 5x 6y 5z 7， )值较小的方程有和.若选用，则用含 y，z 的式子表示 x，并分别代入消去 x，得关于 y，z 的二元一次方程组；若选用，则用含 x，z 的式子表示 y，并分别代入，消去 y，得到关于 x，z 的二元一次方程组，其中选用先消去 y 的解法较简单；解法二(用加减法)：方程组中，相同未知数的系数绝对值之间存在相等或成整数倍的关系时，可用加减法如本题可消去 y.解： 2x 4y 3z 9， 3x 2y 4z 8， 5x 6y 5z 7， )解法一(用代入法)：由，得2y83x4z，y4 x2z.32把代入，得 2x4 3z9，( 432x 2z)即 8x11
11、z25.把代入，得 5x6 5z7，( 432x 2z)即4x7z17.与组成方程组为 8x 11z 25， 4x 7z 17， )解这个方程组，得 x 1，z 3.)把 x1，z3 代入，得 y ，12所以原方程组的解是x 1，y 12，z 3.)解法二(用加减法)：2，得 6x4y8z16.，得 8x11z25.(3)，得9x6y12z24.，得4x7z17.以下解法同解法一，略例 2 解析 (1) 因为三个方程相同未知数的系数之和相等，所以三个x y 7， y z 8， z x 9， )方程相加，除以 2 后，再分别与相减，依次得到 z，x，y 的值；(2) 解法一：由比例的性质，将分别
12、变形为 2x3y 和x y 3 2， y z 5 4， x y z 66， )4y5z；解法二：因为中的 y 的份数分别为 2 份、5 份，其最小公倍数为 10 份，所以将化为 xy1510，将化为 yz108，则 xyz15108，故可设x15k，y10k，z8k(k0)，然后代入中，求出 k 的值，即可求出 x，y，z 的值解： (1) x y 7， y z 8， z x 9， )，得2x2y2z24，xyz12.，得 z5.，得 x4.，得 y3.所以原方程组的解是 x 4，y 3，z 5.)(2)x y 3 2， y z 5 4， x y z 66， )由，得 xy1510，由，得 y
13、z108，所以 xyz15108.设 x15k，y10k，z8k，并代入，得15k10k8k66，所以 k2，所以 x30，y20，z16.所以原方程组的解是 x 30，y 20，z 16.)【课堂总结反思】反思 133解析 解法一：设 x3k，y4k，z5k(k0)，代入 ，得 x 2y 3z2x 3k 8k 15k6k.133解法二：特值法(仅针对填空、选择题)：假设 x3，y4，z5，代入求得 .x 2y 3x2x 133【作业高效训练】课堂达标1 A2解析 A 把 代入四个选项逐一检验x 1，y 1，z 2)3解析 A 把三个方程的两边分别相加，再除以 2，得 xyz6 或将选项逐一代
14、入方程组验证前一种解法称之为直接法；后一种解法称之为逆推验证法4解析 B 2，得 4ab7.故(2)错，选择 B.5 C6答案 z2 x y12 34解析 4z82x3y，z2 x y.12 347答案 1解析 把 代入方程，得 3(1)22m10，得 m1.x 1，y 2，z 1 )8答案 3解析 三个方程相加得 2x2y2z6，所以 xyz3.9答案 (答案不唯一) 2x33x 3y 8，x 3y 5 )x 32 76 5610解析 利用加减法消掉一个未知数，将三元一次方程组转化为二元一次方程组，再进行解答解：(1) 2x y 3z 3， 3x y 2z 1， x y z 5， )由，得
15、3x4x8.由，得 2x3z6.联立，得 3x 4z 8， 2x 3z 6， )解得 x 0，z 2.)把 x0，z2 代入，得 y3.所以原方程组的解是 x 0，y 3，z 2.)(2)依题意，得 Error!x 3y 5，y 2z 5，x z 5， )2，得 2xy15.由组成方程组，得 x 3y 5，2x y 15， )解得 x 8，y 1.)把 x8 代入，得 z3.所以原方程组的解是 x 8，y 1，z 3.)(3)2x 3y z 6， x y 2z 1， x 2y z 5， )，得 3x5y11.2，得 3x3y9.，得 2y2，y1.将 y1 代入，得 3x6，x2.将 x2，y
16、1 代入，得 z1.所以原方程组的解为 x 2，y 1，z 1.)11解：由题意，得 x 2 0，3x 6y 0，3y z 0， )解得 x 2，y 1，z 3， )所以 xyz21(3)0.12解：设甲、乙、丙三个小组分别植树 x 棵、y 棵和 z 棵根据题意，得x y z 50，14(x z) y，x y z， )解得 x 25，y 10，z 15.)答：甲、乙、丙三个小组各植树 25 棵、10 棵和 15 棵13解：依题意，得 解得2x 3y 12，3x 4y 17，3z 27， ) x 3，y 2，z 9.)答：解密得到的明文是 3，2，9.14解：根据规定得 3x2y1， 5x3z8
17、， 3y6z3. |3 y2 x| | x z-3 5| |3 z6 y|所以 3x 2y 1， 5x 3z 8， 3y 6z 3， )2，得 10x3y13.与组成二元一次方程组为 3x 2y 1，10x 3y 13， )解得 把 y1 代入，得 z1，x 1，y 1.)所以原方程组的解为 x 1，y 1，z 1.)数学活动解： x y 3a， y z 5a， z x 4a， )解法 1：，得 zx2a.，得 2z6a，z3a. 把 z3a 分别代入和，得 y2a，xa. 将其代入 x2y3z10，得 a22a33a10，解得 a .x a，y 2a，z 3a.) 53解法 2(技巧解法)：，得 2(xyz)12a，即 xyz6a.，得 z3a；，得 xa；，得 y2a. 以下同解法 1. x a，y 2a，z 3a.)
