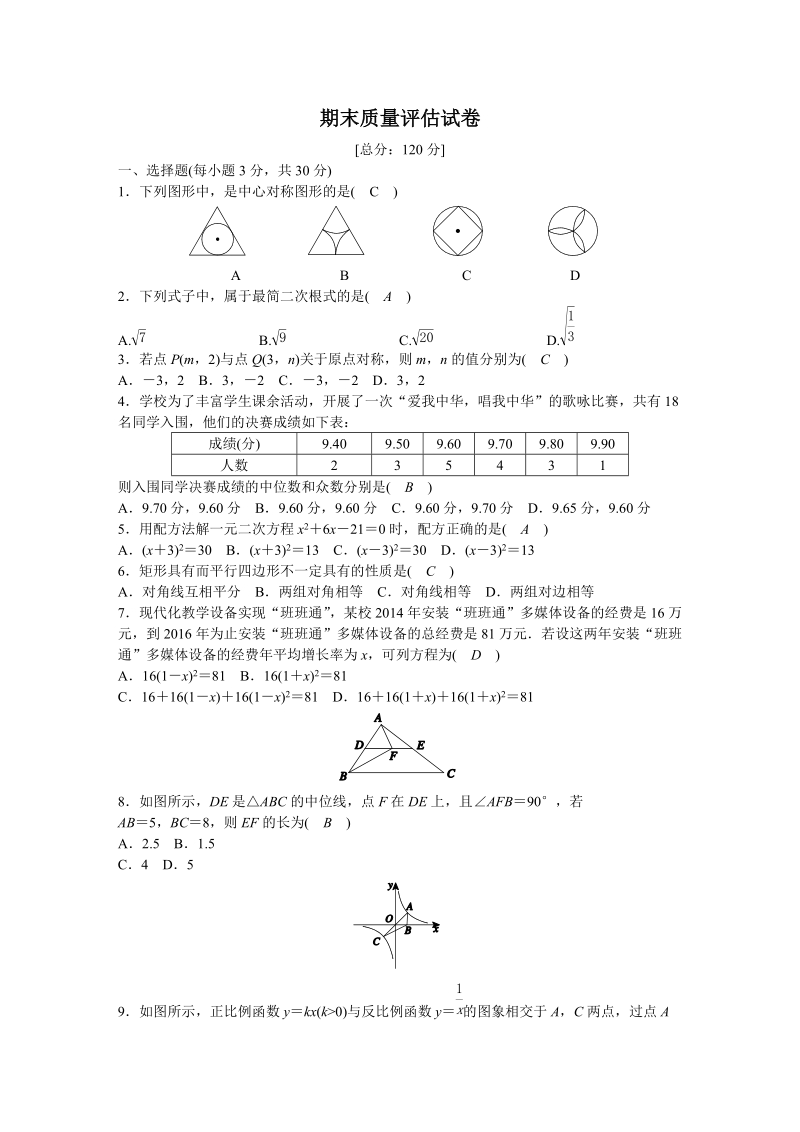
1、期末质量评估试卷总分：120 分一、选择题(每小题 3 分，共 30 分)1下列图形中，是中心对称图形的是( C )A B C D2下列式子中，属于最简二次根式的是( A )A. B. C. D.7 9 20133若点 P(m，2) 与点 Q(3，n)关于原点对称，则 m，n 的值分别为( C )A3，2 B3，2 C 3，2 D3，24学校为了丰富学生课余活动，开展了一次“爱我中华，唱我中华”的歌咏比赛，共有 18名同学入围，他们的决赛成绩如下表：成绩(分) 9.40 9.50 9.60 9.70 9.80 9.90人数 2 3 5 4 3 1则入围同学决赛成绩的中位数和众数分别是( B )
2、A9.70 分，9.60 分 B9.60 分，9.60 分 C9.60 分，9.70 分 D9.65 分，9.60 分5用配方法解一元二次方程 x26x210 时，配方正确的是( A )A(x 3)230 B(x3) 213 C(x3) 230 D(x 3) 2136矩形具有而平行四边形不一定具有的性质是( C )A对角线互相平分 B两组对角相等 C对角线相等 D两组对边相等7现代化教学设备实现“班班通” ，某校 2014 年安装“班班通”多媒体设备的经费是 16 万元，到 2016 年为止安装“班班通”多媒体设备的总经费是 81 万元若设这两年安装“班班通”多媒体设备的经费年平均增长率为 x
3、，可列方程为( D )A16(1x) 281 B16(1x) 281C1616(1x) 16(1x )281 D1616(1 x )16(1x )2818如图所示，DE 是ABC 的中位线，点 F 在 DE 上，且AFB90，若AB5，BC8 ，则 EF 的长为( B )A2.5 B1.5C4 D59如图所示，正比例函数 ykx(k0)与反比例函数 y 的图象相交于 A，C 两点，过点 A1x作 x 轴的垂线交 x 轴于点 B，连结 BC，则ABC 的面积 S( A )A1 B2 C3 D410如图所示，依次连结第一个菱形各边的中点得到一个矩形，再依次连结矩形各边的中点得到第二个菱形，；按此方
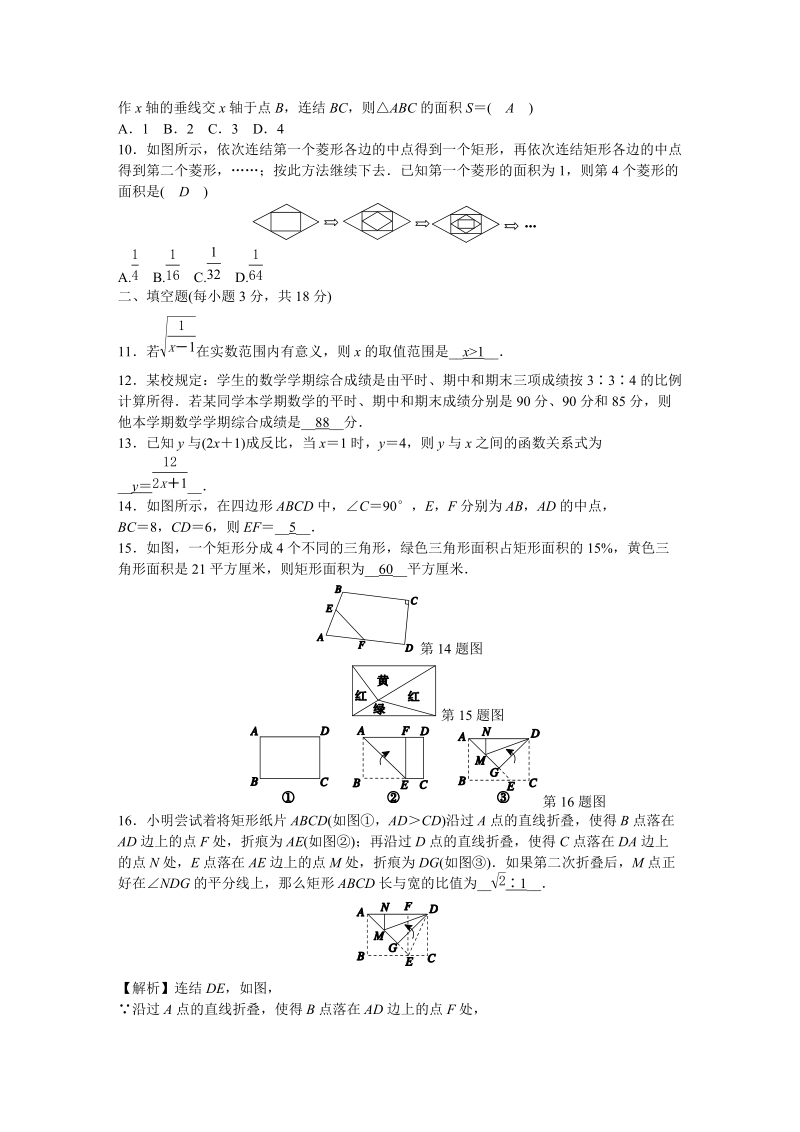
4、法继续下去已知第一个菱形的面积为 1，则第 4 个菱形的面积是( D )A. B. C. D.14 116 132 164二、填空题(每小题 3 分，共 18 分)11若 在实数范围内有意义，则 x 的取值范围是_x1_1x 112某校规定：学生的数学学期综合成绩是由平时、期中和期末三项成绩按 334 的比例计算所得若某同学本学期数学的平时、期中和期末成绩分别是 90 分、90 分和 85 分，则他本学期数学学期综合成绩是_88_分13已知 y 与(2x1)成反比，当 x1 时，y4，则 y 与 x 之间的函数关系式为_y _122x 114如图所示，在四边形 ABCD 中，C90，E ，F
5、分别为 AB，AD 的中点，BC8，CD6，则 EF_5_15如图，一个矩形分成 4 个不同的三角形，绿色三角形面积占矩形面积的 15%，黄色三角形面积是 21 平方厘米，则矩形面积为_60_平方厘米第 14 题图第 15 题图第 16 题图16小明尝试着将矩形纸片 ABCD(如图，AD CD)沿过 A 点的直线折叠，使得 B 点落在AD 边上的点 F 处，折痕为 AE(如图) ；再沿过 D 点的直线折叠，使得 C 点落在 DA 边上的点 N 处，E 点落在 AE 边上的点 M 处，折痕为 DG(如图)如果第二次折叠后，M 点正好在NDG 的平分线上，那么矩形 ABCD 长与宽的比值为_ 1_
6、2【解析】连结 DE，如图，沿过 A 点的直线折叠，使得 B 点落在 AD 边上的点 F 处，四边形 ABEF 为正方形，EAD45.由第二次折叠知，M 点正好在 NDG 的平分线上，DE 平分GDC，RtDGERtDCE，DCDG.又AGD 为等腰直角三角形，AD DG CD， 矩形 ABCD 长与宽的比值2 2 1.2故答案为 1.2三、解答题(8 个小题，共 72 分)17(8 分) 计算：(1)计算：3 ；3 (12 13) 27(2)当 a ，b 时，求代数式 a2abb 2 的值3 2 3 2解：(1)原式3 2 3 ；3 333 3 1133(2)当 a ，b 时，3 2 3 2
7、原式( )2( )( )( )23 2 3 2 3 2 3 252 (32)526 69.18(8 分)(1)把关于 x 的方程(x3)(x3)2x 22x 化为一元二次方程的一般形式，再写出它的二次项系数、一次项系数及常数项；(2)用适当的方法解方程：3(2 x1) 227.解：(1)x 22x90.二次项系数为 1, 一次项系数为2，常数项为 9.(2)原方程化简为 2x13，解得 x11，x 22.19(8 分) 小李和小张参加市田径比赛的校内选拔赛，近期的 8 次测试成绩(分)如下表：测试次数 1 2 3 4 5 6 7 8小李 10 10 11 10 16 14 16 17小张 11
8、 13 13 12 14 13 15 13(1)根据上表数据填写下表：平均分(分) 众数(分) 中位数(分) 方差 (分 2)小李 10 8.25小张 13 13(2)若从中选一人参加市田径比赛，你认为选谁去合适，为什么？解：(1)小李的平均分(10 10111016141617)813(分)，按从小到大顺序排列得到第 4，5 个数分别为 11，14，则中位数(1114)212.5( 分)小张的成绩中出现次数最多的为 13，即众数为 13 分，根据方差公式，得：小张成绩的方差 (1113) 2(1313) 2(13 13) 2(1213)182(1413) 2(13 13) 2(1513) 2
9、(13 13) 21.25(分 2).平均分(分) 众数(分) 中位数(分) 方差(分 2)小李 13 10 12.5 8.25小张 13 13 13 1.25(2)选小张参加市田径比赛合适因为小张的方差较小，所以小张的成绩更稳定( 答案不唯一)20(8 分) 如图，在 ABCD 中，AC 与 BD 交于点 O，点 E，F 都在 BD 上，BEDF .(1)求证：四边形 AECF 是平行四边形；(2)若 ABAC，AB4，AC6，当 AECF 是矩形时，求 BE 的长解：(1)证明：在 ABCD 中，AC 与 BD 交于点 O，AOCO，BODO.BEDF ，EOFO.四边形 AECF 是平行
10、四边形(2)BE221(10 分)(1)如图 1，正方形网格中有一个平行四边形，请在图 1 中画一条直线把平行四边形分成面积相等的两部分，这样的直线能画_条，这些直线都必经过平行四边形的_；(2)把图 2 中的平行四边形分割成四个全等的四边形( 要求在图 2 中画出分割线)，并把所得的四个全等的四边形在图 3 中拼成一个非平行四边形的中心对称图形，且使所得图形的各个顶点都落在格点上解：(1)过平行四边形的对角线的交点任意画一条直线即可，如图 1 所示：这样的直线可以画无数条，这些直线都经过平行四边形的对称中心故答案为无数条，对称中心(2)过平行四边形对边的中点画直线即可，如图 2 所示：把所得
11、的四个全等的四边形在图 3 中拼成一个非平行四边形的中心对称图形如图 3 所示22(9 分) 某印刷厂印刷某尺寸的广告纸，印刷张数为 a(单位：万张)，需按整千张印刷计费，收费规定如下：若 a1：单价为 0.4 元/张若 1a2：每增加 0.1 万张，所有广告纸每张减少 0.01 元，费用再 9 折优惠若 a2：每增加 0.1 万张，所有广告纸每张减少 0.02 元，费用再 8 折优惠(1)若某客户要印刷广告纸 1.5 万张，则该客户需支付费用 _元；(2)若某客户支付了广告纸费用 0.6 万元，求印刷张数 a 的值解：(1)由题意，得(0.40.05)0.915 0004 725(元) ；故
12、答案为 4 725.(2)当 a2 时，(0.40.1)0.920.54 万元5 400(元)，则某客户支付了广告纸费用 0.6 万元时，总的印刷张数超过 2 万张，故 a 0.80.6，(0.4 a 20.1 0.02)整理，得 4a216a150，解得 a11.5(不合题意，舍去 )，a 22.5，答：印刷张数 a 的值为 2.5.23(9 分) 如图所示，在四边形 ABCD 中，对角线 AC，BD 相交于点 O，O 为 AC，BD 的中点，AB10，AC16，BD 12.(1)四边形 ABCD 是什么特殊的四边形？请证明(2)点 P 在 AO 上，点 Q 在 DO 上，且 AP2OQ.若
13、 PQ BQ，求 AP 的长解：(1)四边形 ABCD 是菱形证明如下：O 为 AC，BD 的中点，OAOC AC8，OB OD BD6.12 12四边形 ABCD 是平行四边形AO 2BO 2100，AB 2100 ，AO 2BO 2AB 2，AOB90，ACBD.平行四边形 ABCD 是菱形(2)设 OQx，则 AP2x ，OP82x，PQBQ6x.在 RtPOQ 中，OP 2OQ 2PQ 2，(82x) 2x 2(6x) 2解得 x1 (舍去)，x 2 .11 932 11 932AP2 11 .11 932 9324(12 分) 如图 1，已知点 A(1，0)，B(0 ，2)， ABC
14、D 的边 AD 与 y 轴交于点 E，且 E为 AD 中点，双曲线 y 经过 C，D 两点kx(1)直接写出 k 的值_；(2)点 P 在双曲线 y 上，点 Q 在 y 轴上，若以点 A，B，P，Q 为顶点的四边形是平行四边kx形，试求出满足要求的所有点 P，Q 的坐标；(3)以线段 AB 为对角线作正方形 AFBH(如图 3)，T 是边 AF 上一动点，M 是 HT 的中点，MNHT，交 AB 于点 N，当 T 点在 AF 上运动时， 的值是否发生改变？若改变，求出其MNHT变化范围；若不改变，请求出其值，并给出你的证明解：(1)A( 1，0)，B(0 ，2) ，E 为 AD 中点，D 的横
15、坐标为 1.设 D(1，t) ，又DCAB ， C(2，t 2) ，t 2t4.t4，k 4；故答案为 4.(2)由(1)知 k 4，反比例函数的表达式为 y .4x点 P 在双曲线 y 上，点 Q 在 y 轴上，设 Q(0，y)， P .kx (x， 4x)当 AB 为边时：如图 1 所示，若 ABPQ 为平行四边形，则 0，解得 x1，此时 P1(1，4)，Q 1(0，6)； 1 x2如图 2 所示，若 ABQP 为平行四边形，则 ，解得x1，此时 P2(1，4)， 12 x2Q2(0，6) ；如图 3 所示，当 AB 为对角线时，APBQ，且 APBQ. ，解得 x1，P 3(1，4)，
16、Q 3(0，2) ； 12 x2故 P1(1，4) ，Q 1(0，6)；P 2(1，4) ，Q 2(0，6)；P 3( 1，4) ，Q 3(0，2) (3) 的值不发生变化理由：MNHT如图 4，连结 NH，NT，NF，MN 是线段 HT 的垂直平分线，NTNH.四边形 AFBH 是正方形，ABFABH.在BFN 与BHN 中， BF BH， ABF ABH，BN BN， )BFNBHN(SAS)，NF NHNT，NTFNFTAHN.在四边形 ATNH 中，ATNNTF180，而NTFNFTAHN，ATNAHN180.四边形 ATNH 内角和为 360，TNH 3601809090.MN HT， .12 MNHT 12
