1、2019年葫芦岛市龙港区毕业升学考试模拟卷数学卷一、选择题（每小题 3分，共 21分）1 的相反数是（ ）A B C D2在平面直角坐标系中，点（1，2）所在的象限是（ ）A第一象限 B第二象限 C第三象限 D第四象限3如图，A.B.C 是O 上的三点，BAC30，则BOC 的大小是（ ）A30 B60 C90 D454一元二次方程 x2+2x+40 的根的情况是（ ）A有一个实数根 B有两个相等的实数根C有两个不相等的实数根 D没有实数根5在 RtABC 中，C90，a1，c4，则 sinA的值是（ ）A B C D6如图，直线 ykx+b 与 x轴交于点（4，0） ，则 y0 时，x 的取
2、值范围是（ ）Ax4 Bx0 Cx4 Dx07将一圆形纸片对折后再对折，得到下图，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是（ ）A B C D二、填空题（本题共 7小题，每小题 3分，共 21分）说明：将下列各题结果直接填在题后的横线上8早春二月的某一天，大连市南部地区的平均气温为3，北部地区的平均气温为6，则当天南部地区比北部地区的平均气温高_9在函数 y 中，自变量 x的取值范围是_10关于 x的一元二次方程 x2+bx+c0 的两根为 x11，x22，则 x2+bx+c分解因式的结果为_11如图，O 的半径为 5cm，圆心 O到 AB的距离为 3cm，则弦 AB长
3、为_ cm12大连市内与庄河两地之间的距离是 160千米，若汽车以平均每小时 80千米的速度从大连市内开往庄河，则汽车距庄河的路程 y（千米）与行驶的时间 x（小时）之间的函数关系式为 13边长为 6 的正六边形外接圆半径是_14将一个底面半径为 2，高为 4的圆柱形纸筒沿一条母线剪开，所得到的侧面展开图形面积为 _三、解答题（本题共 6小题，其中 15.16题各 8分，17.18.19 题各 10分，20 题 12分，共58分）15 （8 分）反比例函数 的图象经过点 A（2，3） （1）求这个函数的解析式；（2）请判断点 B（1，6）是否在这个反比例函数的图象上，并说明理由16 （8 分）
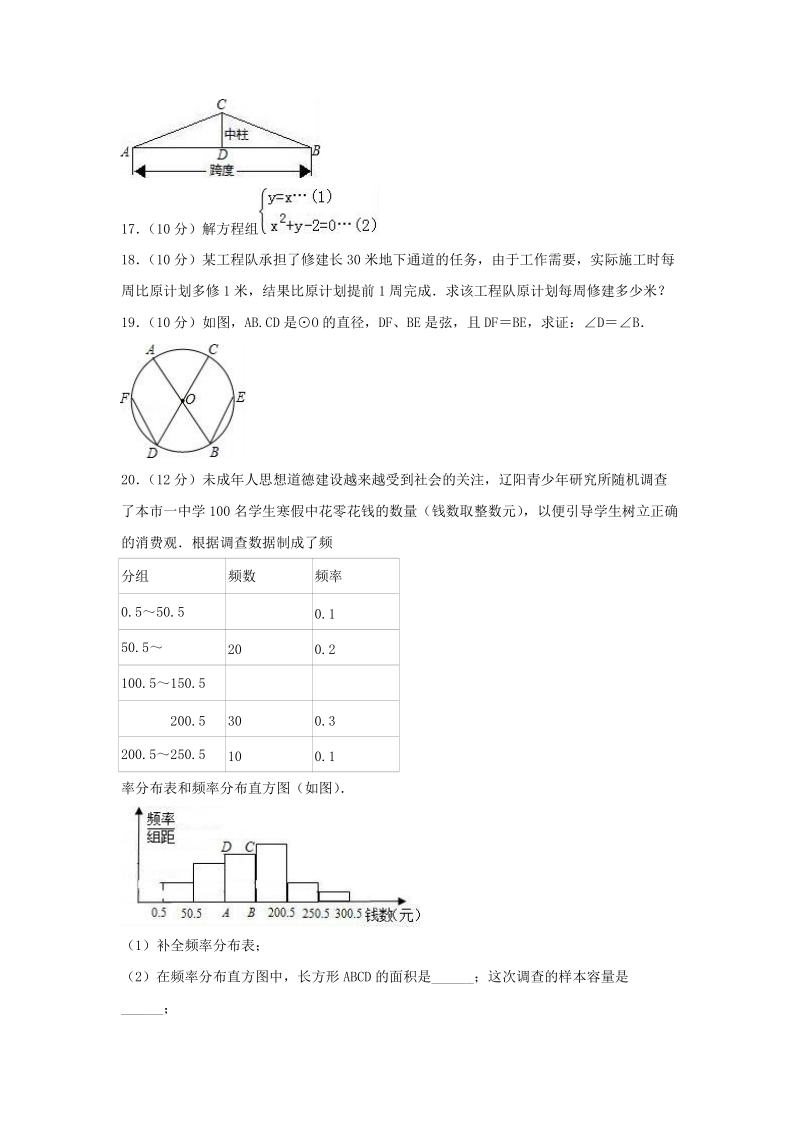
4、如图，某校自行车棚的人字架棚顶为等腰三角形，D 是 AB的中点，中柱 CD1米，A27，求跨度 AB的长（精确到 0.01米）17 （10 分）解方程组18 （10 分）某工程队承担了修建长 30米地下通道的任务，由于工作需要，实际施工时每周比原计划多修 1米，结果比原计划提前 1周完成求该工程队原计划每周修建多少米？19 （10 分）如图，AB.CD 是O 的直径，DF、BE 是弦，且 DFBE，求证：DB20 （12 分）未成年人思想道德建设越来越受到社会的关注，辽阳青少年研究所随机调查了本市一中学 100名学生寒假中花零花钱的数量（钱数取整数元） ，以便引导学生树立正确的消费观根据调查数
5、据制成了频 分组 频数 频率0.550.5 0.150.5 20 0.2100.5150.5 200.5 30 0.3200.5250.5 10 0.1率分布表和频率分布直方图（如图） （1）补全频率分布表；（2）在频率分布直方图中，长方形 ABCD的面积是_；这次调查的样本容量是_；（3）研究所认为，应对消费 150元以上的学生提出勤俭节约的建议试估计应对该校1000名学生中约多少名学生提出这项建议四、解答题（本题共 3小题，其中 21题 7分，22 题 8分，23 题 9分，共 24分）21 （7 分）如图，抛物线 yx2+5x+n 经过点 A（1，0） ，与 y轴交于点 B（1）求抛物线
6、的解析式；（2）P 是 y轴正半轴 上一点，且PAB 是以 AB为腰的等腰三角形，试求 P点坐标22 （8 分）如图 1，图 2、图 m是边长均大于 2的三角形、四边形、凸 n边形分别以它们的各顶点为圆心，以 1为半径画弧与两邻边相交，得到 3条弧、4 条弧、n 条弧（1）图 1中 3条弧的弧长的和为_，图 2中 4条弧的弧长的和为_；（2）求图 m中 n条弧的弧长的和（用 n表示） 23 （9 分）4100 米拉力赛是学校运动会最精彩的项目之一图中的实线和虚线分别是初三一班和初三二班代表队在比赛时运动员所跑的路程 y（米）与所用时间 x（秒）的函数图象（假设每名运动员跑步速度不变，交接棒时间
7、忽略不计） 问题：（1）初三二班跑得最快的是第_接力棒的运动员；（2）发令后经过多长时间两班运动员第一次并列？五、解答题和附加题（解答题共 3小题，其中 24.25题各 8分，26 题 10分，共 26分；）24 （8 分）如图，O 的直径 DF与弦 AB交于点 E，C 为O 外一点，CBAB，G 是直线 CD上一点，ADGABD求证：ADCEDEDF；说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来（要求至少写 3步） ；（2）在你经历说明（1）的过程之后，可以从下列、中选取一个补充或更换已知条件，完成你的证明注意：选取完成证明得 8分；选取完成证
8、明得 6分；选取完成证明得 4分CDBCEB；ADEC；DECADF，且CDE9025 （8 分）阅读材料，解答问题材料：“小聪设计的一个电子游戏是：一电子跳蚤从这 P1（3，9）开始，按点的横坐标依次增加 1的规律，在抛物线 yx2 上向右跳动，得到点 P2.P3.P4.P5（如图 1所示）过 P1.P2.P3分 别作 P1H1.P2H2.P3H3垂直于 x轴，垂足为 H1.H2.H3，则 SP1P2P3S梯形 P1H1H3P3S 梯形 P1H1H2P2S 梯形 P2H2H3P3 （9+1）2 （9+4）1 （4+1）1，即P1P2P3 的面积为 1 ”问题：（1）求四边形 P1P2P3P4
9、和 P2P3P4P5的面积（要求：写出其中一个四边形面积的求解过程，另一个直接写出答案） ；（2）猜想四边形 Pn1PnPn+1Pn+2 的面积，并说明理由（利用图 2） ；（3）若将抛物线 yx2 改为抛物线 yx2+bx+c，其它条件不变，猜想四边形Pn1PnPn+1Pn+2 的面积（直接写出答案） 26 （10 分）初三（5）班综合实践小组去湖滨花园测量人工湖的长，如图 A.D是人工湖边的两座雕塑，AB.BC 是湖滨花园的小路，小东同学进行如下测量，B 点在 A点北偏东 60方向，C 点在 B点北偏东 45方向，C 点在 D点正东方向，且测得 AB20 米，BC40 米，求 AD的长 （
10、 1.732， 1.414，结果精确到 0.01米）参考答案一、选择题1 的相反数是（ ）A B C D【分析】一个数的相反数就是在这个数前面添上“”号，由此即可求解解： 的相反数是 故选：B【点评】本题考查了相反数的意义，一个数的相反数就是在这个数前面添上“”号：一个正数的相反数是负数，一个负数的相反数是正数，0 的相反数是 02在平面直角坐标系中，点（1，2）所在的象限是（ ）A第一象限 B第二象限 C第三象限 D第四象限【分析】根据横纵坐标的符号可得相关象限解：点的横纵坐标均为负数，点（1，2）所在的象限是第三象限故选：C【点评】考查点的坐标的相关知识；用到的知识点为：横纵坐标均为负数的
11、点在第三象限3如图，A.B.C 是O 上的三点，BAC30，则BOC 的大小是（ ）A30 B60 C90 D45【分析】欲求BOC，又已知一圆周角BAC，可利用圆周角与圆心角的关系求解解：BAC30，BOC60（同弧所对的圆周角是圆心角的一半） 故选：B【点评】本题考查了圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半4一元二次方程 x2+2x+40 的根的情况是（ ）A有一个实数根 B有两个相等的实数根C有两个不相等的实数根 D没有实数根【分析】判断上述方程的根的情况，只要看根的判别式b24ac 的值的符号就可以了解：a1，b2，c4，b24ac224
12、14120，方程没有实数根故选：D【点评】总结：一元二次方程根的情况与判别式的关系：（1）0方程有两个不相等的实数根；（2）0方程有两个相等的实数根；（3）0方程没有实数根5在 RtABC 中，C90，a1，c4，则 sinA的值是（ ）A B C D【分析】由三角函数的定义，在直角三角形中，正弦等于对边比斜边易得答案解：根据题意，由三角函数的定义可得 sinA ，则 sinA ；故选：B【点评】本题考查锐角三角函数的概念：在直角三角形中，正弦等于对边比斜边；余弦等于邻边比斜边；正切等于对边比邻边6如图，直线 ykx+b 与 x轴交于点（4，0） ，则 y0 时，x 的取值范围是（ ）Ax4
13、Bx0 Cx4 Dx0【分析】根据题意，y0，即 x轴上方的部分，读图易得答案解：由函数图象可知 x4 时 y0故选：A【点评】本题较简单，解答此类题目时应注意数形结合的思想是问题更直观化7将一圆形纸片对折后再对折，得到下图，然后沿着图中的虚线剪开，得到两部分，其中一部分展开后的平面图形是（ ）A B C D【分析】严格按照图中的方法亲自动手操作一下，即可很直观地呈现出来解：根据题意知，剪去的纸片一定是一个四边形，且对角线互相垂直故选：C【点评】本题主要考查学生的动手能力及空间想象能力对于此类问题 ，学生只要亲自动手操作，答案就会很直观地呈现二、填空题（本题共 7小题，每小题 3分，共 21分
14、）说明：将下列各题结果直接填在题后的横线上8早春二月的某一天，大连市南部地区的平均气温为3，北部地区的平均气温为6，则当天南部地区比北部地区的平均气温高 3 【分析】用南部气温减北部的气温，根据“减去一个数等于加上这个数的相反数”求出它们的差就是高出的温度解：（3）（6）3+63答：当天南部地区比北部地区的平均气温高 3【点评】本题主要考查有理数的减法运算法则减法运算法则：减去一个数等于加上这个数的相反数9在函数 y 中，自变量 x的取值范围是 x1 【分析】因为当函数表达式是二次根式时，被开方数为非负数，所以 x10，解不等式可求 x的范围解：根据题意得：x10，解得：x1故答案为：x1【点
15、评】此题主要考查函数自变量的取值范围，解决本题的关键是当函数表达式是二次根式时，被开方数为非负数10关于 x的一元二次方程 x2+bx+c0 的两根为 x11，x22，则 x2+bx+c分解因式的结果为 （x1） （x2） 【分析】已知了方程的两根，可以将方程化为：a（xx1） （xx2）0（a0）的形式，对比原方程即可得到所求代数式的因式分解的结果解：已知方程的两根为：x11，x22，可得：（x1） （x2）0，x2+bx+c（x1） （x2） 【点评】一元二次方程 ax2+bx+c0（a0，A.B.c 是常数） ，若方程的两根是 x1和 x2，则 ax2 +bx+ca（xx1） （xx2）
16、11如图，O 的半径为 5cm，圆心 O到 AB的距离为 3cm，则弦 AB长为 8 cm【分析】连接 OA，由 OC垂直于弦 AB，利用垂径定理得到 C为 AB的中点，在直角三角形AOC中，由 OA与 OC的长，利用勾股定理求出 AC的长，即可得出 AB的长解：连接 OA，OCAB，C 为 AB的中点，即 ACBC，在 RtAOC 中，OA5cm，OC3cm，根据勾股定理得：AC 4cm，AB2AC8cm故答案为：8【点评】本题考查的是垂径定理，根据题意作出辅助线，构造出直角三角形是解答此题的关键12大连市内与庄河两地之间的距离是 160千米，若汽车以平均每小时 80千米的速度从大连市内开往
17、庄河，则汽车距庄河的路程 y（千米）与行驶的时间 x（小时）之间的函数关系式为 y16080x（0x2） 【分析】汽车距庄河的路程 y（千米）原来两地的距离汽车行驶的距离解：汽车的速度是平均每小时 80千米，它行驶 x小时走过的路程是 80x，汽车距庄河的路程 y16080x（0x2） 【点评】此题主要考查了根据实际问题确定一次函数的解析式，找到所求量的等量关系是解决问题的关键13边长为 6的正六边形外接圆半径是 6 【分析】根据正六边形的外接圆半径和正六边形的边长将组成一个等边三角形，即可求解解：正 6边形的中心角为 360660，那么外接圆的半径和正六边形的边长将组成一个等边三角形，边长为
18、 6的正六边形外接圆半径是 6【点评】正六边形的外接圆半径和正六边形的边长将组成一个等边三角形14将一个底面半径为 2，高为 4的圆柱形纸筒沿一条母线剪开，所得到的侧面展开图形面积为 16 【分析】圆柱侧面积底面周长高，按公式代入即可解：圆柱形纸筒沿一条母线剪开，所得到的侧面展开图形是矩形，其长是圆柱的底面周长4，宽为圆柱的高 4，所以所得到的侧面展开图形面积为 4416【点评】圆柱的侧面展开图形是矩形，它的面积圆柱的底面周长圆柱的高三、解答题（本题共 6小题，其中 15.16题各 8分，17.18.19 题各 10分，20 题 12分，共58分）15 （8 分）反比例函数 的图象经过点 A（
19、2，3） （1）求这个函数的解析式；（2）请判断点 B（1，6）是否在这个反比例函数的图象上，并说明理由【分析】 （1）先把 A点的坐标代入反比例函数 y 中，求出 k，即可求出函数解析式；（2）再把 B点的横坐标代入反比例函数的解析式，可求出 y，若 y的值与 B点的纵坐标相等，则说明 B在函数的图象上，否则就不在函数图象上解：（1）把（2，3）代入 y 中得3 ，k6，函数的解析式是 y ；（2）把 x1 代入 y 中得 y6，点 B在此函数的图象上【点评】本题考查了待定系数法求反比例函数的解析式、反比例函数图象上点的坐标特征此题比较容易掌握16 （8 分）如图，某校自行车棚的人字架棚顶为
20、等腰三角形，D 是 AB的中点，中柱 CD1米，A27，求跨度 AB的 长（精确到 0.01米） www.*zz&【分析】想求得 AB长，由等腰三角形的三线合一定理可知 AB2AD，求得 AD即可，而 AD可以利用A 的三角函数可以求出解：ACBC，D 是 AB的中点，CDAB，又CD1 米，A27，ADCDtan271.96，AB2AD，AB3.93m【点评】此题主要考查了三角函数，直角三角形，等腰三角形等知识，关键利用了正切函数的定义求出 AD，然后就可以求出 AB17 （10 分）解方程组【分析】第一个方程的系数为 1，可直接代入第二个方程解：把（1）代入（2）得：x2+x20，（x+2
21、） （x1）0，解得：x2 或 1，当 x2 时，y2，当 x1 时，y1，原方程组的解是 或 【点评】当二元一次方程组的两个方程里有一个未知数的系数的绝对值为 1的时候，可选择用代入法求解18 （10 分）某工程队承担了修建长 30米地下通道的任务，由于工作需要，实际施工时每周比原计划多修 1米，结果比原计划提前 1周完成求该工程队原计划每周修建多少米？【分析】本题用到的等量关系是工作时间工作总量工作效率，可根据实际施工用的时间+1 周原计划用的时间，来列方程求解解：设该工程队原计划每周修建 x米由题意得： +1整理得：x2+x300解得：x15，x26（不合题意舍去） 经检验：x 5 是原
22、方程的解答：该工程队原计划每周修建 5米【点评】找到合适的等量关系是解决问题的关键本题用到的等量关系为：工作时间工作总量工作效率，可根据题意列出方程，判断所求的解是否符合题意，舍去不合题意的解19 （10 分）如图，AB.CD 是O 的直径，DF、BE 是弦，且 DFBE，求证：DB【分析】根据在同圆中等弦对的弧相等，AB.CD 是O 的直径，则弧 CFD弧 AEB，由FDEB，得，弧 FD弧 EB，由等量减去等量仍是等量得：弧 CFD弧 FD弧 AEB弧 EB，即弧 FC弧 AE，由等弧对的圆周角相等，得DB方法（一）证明：AB.CD 是O 的直径，弧 CFD弧 AEBFDEB，弧 FD弧
23、EB弧 CFD弧 FD弧 AEB弧 EB即弧 FC弧 AEDB方法（二）证明：如图，连接 CF，AEAB.CD 是O 的直径，FE90（直径所对的圆 周角是直角） ABCD，DFBE，RtDFCRtBEA（HL） DB【点评】本题利用了在同圆中等弦对的弧相等，等弧对的弦，圆周角相等，等量减去等量仍是等量求解20 （12 分）未成年人思想道德建设越来越受到社会的关注，辽阳青少年研究所随机调查了本市一中学 100名学生寒假中花零花钱的数量（钱数取整数元） ，以便引导学生树立正确的消费观根据调查数据制成了频 分组 频数 频率0.550.5 0.150.5 20 0.2100.515 0.5 200.
24、5 30 0.3200.5250.5 10 0.1率分布表和频率分布直方图（如图） （1）补全频率分布表；（2）在频率分布直方图中，长方形 ABCD的面积是 0.25 ；这次调查的样本容量是 100 ；（3）研究所认为，应对消费 150元以上的学生提出勤俭节约的建议试估计应对该校1000名学生中约多少名学生提出这项建议【分析】 （1）0.550.5 的频数1000.110，由各组的频率之和等于 1可知：10 0.5150.5 的频率10.10.20.30.10.050.25，则频数1000.2525；（2）在频率分布直方图中，长方形 ABCD的面积为 500.2512.5，这次调查的样本容量是
25、 100；（3）研究所认为，应对消费 150元以上的学生提出勤俭节约的建议试估计应对该校1000名学生提出这项建议的人数1000（0.3+0.1+0.05）450 人解：（1）填表如下：（2）长方形 ABCD的面积为 0.25，样本容量是 100；（3）提出这项建议的人数1000（0.3+0.1+0.05）450 人【点评】记住公式：频率频数总人数，是解决本题的关键，同时要会应用用样本估计总体这种方法四、解答题（本题共 3小题，其中 21题 7分，22 题 8分，23 题 9分，共 24分）21 （7 分）如图，抛物线 yx2+5x+n 经过点 A（1，0） ，与 y轴交于点 B（1）求抛物线
26、的解析式；（2）P 是 y轴正半轴上一点，且PAB 是以 AB为腰的等腰三角形，试求 P点坐标【分析】 （1）将 A点的坐标代入抛物线中，即可得出二次函数的解析 式；（2）本题要分两种情况进行讨论： PBAB，先根据抛物线的解析式求出 B点的坐标，即可得出 OB的长，进而可求出 AB的长，也就知道了 PB的长，由此可求出 P点的坐标；PAAB，此时 P与 B关于 x轴对称，由此可求出 P点的坐标解：（1）抛物线 yx2+5x+n 经过点 A（1，0）n4yx2+5x4；（2）抛物线的解析式为 yx2+5x4，令 x0，则 y4，B 点坐标（0，4） ，AB ，当 PBAB 时，PBAB ，OP
27、PBOB 4P（0， 4）当 PAAB 时，P、B 关于 x轴对称，P（0，4）因此 P点的坐标为（0， 4）或（0，4） 【点评】本题考查了二次函数解析式的确定、等腰三角形的构成等知识点，主要考查学生分类讨论、数形结合的数学思想方法22 （8 分）如图 1，图 2、图 m是边长均大于 2的三角形、四边形、凸 n边形分别以它们的各顶点为圆心，以 1为半径画弧与两邻边相交，得到 3条弧、4 条弧、n 条弧 （1）图 1中 3条弧的弧长的和为 ，图 2中 4条弧的弧长的和为 2 ；（2）求图 m中 n条弧的弧长的和（用 n表示） 【分析】 （1）利用弧长公式和三角形和四边形的内角和公式代入计算；（
28、2）利用多边形的内角和公式和弧长公式计算解：（1）利用弧长公式可得+ + ，因为 n1+n2+n3180同理，四边形的 + + + 2，因为四边形的内角和为 360度；（2）n 条弧 + + + + （n2）【点评】本题综合考查了多边形的内角和和弧长公式的应用23 （9 分）4100 米拉力赛是学校运动会最精彩的项目之一图中的实线和虚线分别是初三一班和初三二班代表队在比赛时运动员所跑的路程 y（米）与所用时间 x（秒）的函数图象（假设每名运动员跑步速度不变，交接棒时间忽略不计） 问题：（1）初三二班跑得最快的是第 1 接力棒的运动员；（2）发令后经过多长时间两班运动员第一次并列？【分析】 （1
29、）直接根据图象上点横坐标可知道最快的是第 1接力棒的运动员用了 12秒跑完100米；（2）分别利用待定系数法把图象相交的部分，一班，二班的直线解析式求出来后，联立成方程组求交点坐标即可解：（1）从函数图象上可看出初三二班跑得最快的是第 1接力棒的运动员用了 12秒跑完100米；（2）设在图象相交的部分，设一班的直线为 y1kx+b，把点（28，200） ， （40，300）代入得：解得：k ，b ，即 y1 x ，二班的为 y2kx+b，把点（25，200） ， （41，300） ，代入得：解得：k ，b ，即 y2 x+联立方程组 ，解得： ，所以发令后第 37秒两班运动员在 275米处第一
30、次并列【点评】主要考查利用一次函数的模型解决实际问题的能力和读图能力要先根据题意列出函数关系式，再代数求值解题的关键是要分析题意根据实际意义准确的列出解析式，再把对应值代入求解，并会根据图示得出所需要的信息要掌握利用函数解析式联立成方程组求交点坐标的方法五、解答题和附加题（解答题共 3小题，其中 24.25题各 8分，26 题 10分，共 26分；）24 （8 分）如图，O 的直径 DF与弦 AB交于点 E，C 为O 外一点，CBAB，G 是直线 CD上一点，ADGABD求证：ADCEDEDF；说明：（1）如果你经历反复探索，没有找到解决问题的方法，请你把探索过程中的某种思路过程写出来（要求至
31、少写 3步） ；（2）在你经历说明（1）的过程之后，可以从下列、中选取一个补充或更换已知条件，完成你的证明注意：选取完成证明得 8分；选取完成证明得 6分；选取完成证明得 4分CDBCEB；ADEC；DECADF，且CDE90【分析】连接 AF，由直径所对的圆周角是直角、同弧所对的圆周角相等的性质，证得直线CD是O 的切线，若证 ADCEDEDF，只要征得ADFDEC 即可在第一问中只能证得EDCDAF90，所以在第二问中只要证得DECADF 即可解答此题（1）证明：连接 AF，DF 是O 的直径，DAF90，F+ADF90，FABD，ADGABD，FADG，ADF+ADG90直线 CD是O
32、的切线EDC90，EDCDAF90；（2）选取完成证明证明：直线 CD是O 的切线，CDBACDBCEB，ACEBADECDECADFEDCDAF90，ADFDECAD：DEDF：ECADCEDEDF【点评】此题考查了切线的性质与判定、弦切角定理、相似三角形的判定与性质等知识注意乘积的形式可以转化为比例的形式，通过证明三角形相似得出还要注意构造直径所对的圆周角是圆中的常见辅助线25 （8 分）阅读材料，解答问题材料：“小聪设计的一个电子游戏是：一电子跳蚤从这 P1（3，9）开始，按点的横坐标依次增加 1的规律，在抛物线 yx2 上向右跳动，得到点 P2.P3.P4.P5（如图 1所示）过 P1
33、.P2.P3分别作 P1H1.P2H2.P3H3垂直于 x轴，垂足为 H1.H2.H3，则 SP1P2P3S梯形 P1H1H3P3S 梯形 P1H1H2P2S 梯形 P2H2H3P3 （9+1）2 （9+4）1 （4+1）1，即P1P2P3 的面积为 1 ”问题：（1）求四边形 P1P2P3P4和 P2P3P4P5的面积（要求：写出其中一个四边形面积的求解过程，另一个直接写出答案） ；（2）猜想四边形 Pn1PnPn+1Pn+2 的面积，并说明理由（利用图 2） ；（3）若将抛物线 yx2 改为抛物线 yx2+bx+c，其它条件不变，猜想四边形Pn1PnPn+1Pn+2 的面积（直接写出答案）
34、 【分析】 （1）作 P5H5垂直于 x轴，垂足为 H5，把四边形 P1P2P3P4和四边形 P2P3P4P5的转化为 SP1P2P3P4SOP1H1SOP3H3S 梯形 P2H2H3P3S 梯形 P1H1H2P2和SP2P3P4P5S 梯形 P5H5H2P2SP5H5OSOH3P3S 梯形 P2H2H3P3来求解；（2） （3）由图可知，Pn1.Pn、Pn+1.Pn+2 的横坐标为 n5，n4，n3，n2，代入二次函数解析式，可得 Pn1.Pn、Pn+1.Pn+2 的纵坐标为（n5）2， （n4）2， （n3）2， （n2）2，将四边形面积转化为 S四边形 Pn1PnPn+1Pn+2S 梯形
35、 Pn5Hn5Hn2Pn2S 梯形Pn5Hn5Hn4Pn4S 梯形 Pn4Hn4Hn3Pn3S 梯形 Pn3Hn3Hn2Pn2 来解答解：（1）作 P5H5垂直于 x轴，垂足为 H5，由图可知 SP1P2P3P4SOP1H1SOP3H3S 梯形 P2H2H3P3S 梯形 P1H1H2P2 4，SP2P3P4P5S 梯形 P5H5H2P2SP5H5OSOH3P3S 梯形P2H2H3P3 4；（2）作 Pn1Hn1.PnHn、Pn+1Hn+1.Pn+2Hn+2 垂直于 x轴，垂足为Hn1.Hn、Hn+1.Hn+2，由图可知 Pn1.Pn、Pn+1.Pn+2 的横坐标为 n5，n4，n3，n2，代入
36、二次函数解析式，可得 Pn1.Pn、Pn+1.Pn+2 的纵坐标为（n5）2， （n4）2， （n3）2， （n2）2，四边形 Pn1PnPn+1Pn+2 的面积为 S四边形 Pn1PnPn+1Pn+2S 梯形 Pn5Hn5Hn2Pn2S 梯形 Pn5Hn5Hn4Pn4S 梯形Pn4Hn4Hn3Pn3S 梯形 Pn3Hn3Hn2Pn2 4；（3）S 四边形 Pn1PnPn+1Pn+2S 梯形 Pn5Hn5Hn2Pn2S 梯形 Pn5Hn5Hn4Pn4S 梯形Pn4Hn4Hn3Pn3S 梯形 Pn3Hn3Hn2Pn2 4【点评】此题是一道材料分析题，考查了根据函数坐标特点求图形面积的知识解答时要
37、注意，前一小题为后面的题提供思路，由于计算量极大，要仔细计算，以免出错，26 （10 分）初三（5）班综合实践小组去湖滨花园测量人工湖的长，如图 A.D是人工湖边的两座雕塑，AB.BC 是湖滨花园的小路，小东同学进行如下测量，B 点在 A点北偏东 60方向，C 点在 B点北偏东 45方向，C 点在 D点正东方向，且测得 AB20 米，BC40 米，求 AD的长 （ 1.732， 1.414，结果精确到 0.01米）【分析】过点 B作 BEDA，BFDC，垂足分别为 E.F，已知 ADAE+ED，则分别求得 AE.DE的长即可求得 AD的长解：过点 B作 BEDA，BFDC，垂足分别为 E，F，由题意知，ADCD四边形 BFDE为矩形BFED在 RtABE 中，AEABcosEAB在 RtBCF 中，BFBCcosFBCADAE+BF20cos60+40cos4520 +40 10+2010+201.41438.28（米） 即 AD38.28 米【点评】解一般三角形，求三角形的边或高的问题一般可以转化为解直角三角形的 问题，解决的方法就是作高线
