1、2019 年春人教新版七年级数学下册 第六章 实数 单元测试题一选择题（共 10 小题）164 的平方根是（ ）A8 B4 C8 D42 的值是（ ）A4 B2 C4 D23 的立方根是（ ）A4 B2 C2 D84下列说法正确的是（ ）A144 的平方根等于 12 B25 的算术平方根等于 5C 的平方根等于4 D 的等于35下列说法错误的是（ ）A5 是 25 的算术平方根B1 是 1 的一个平方根C9 的立方根是 3D0 的平方根与算术平方根都是 06若将 ， ， 、 四个无理数表示在数轴上，其中能被如图所示的墨迹覆盖的数是（ ）A B C D7在数轴上，与表示 的点距离最近的整数点所表
2、示的数是（ ）A1 B2 C3 D48如图，已知数轴上的点 A，B，0，C ，D，E 分别表示数3、2、0、1、2、3，则表示数1 的点 P 应落在线段（ ）AAB 上 BOC 上 CCD 上 DDE 上9在实数 0.23，4. ， ， ，0.3030030003（每两个 3 之间增加 1 个 0）中，无理数的个数是（ ）A1 个 B2 个 C3 个 D4 个10如果 x 的立方根是 3，那么 x 的值为（ ）A3 B9 C D27二填空题（共 8 小题）11若一个正数的两个平方根分别为 1，1，则这个正数是 12根据如图所示的计算程序，若输入的 x 的值为 ，则输出的 y 的值为 13（1.
3、44） 2 的算术平方根为 ； 的平方根为 ； 14已知一个正数的两个平方根分别为 2m6 和 3+m，则 m9 的立方根是 15某个正数的平方根是 x 与 y，3x y 的立方根是 2，则这个正数是 16如果一个数的立方根是 4，那么这个数的算术平方根是 17数轴上到 这点距离为 的点表示的数是 18写一个比 4 小的无理数 三解答题（共 8 小题）19计算： + +|1 |20已知 A 是 m+n+4 的算术平方根，B 是 m+2n 的立方根，求 BA 的立方根21已知下列一组数：， （1）将这组数分类填入相应的大括号内1 分数集合： ；2 无理数集合： ；3 非负数集合： （2）在数轴上
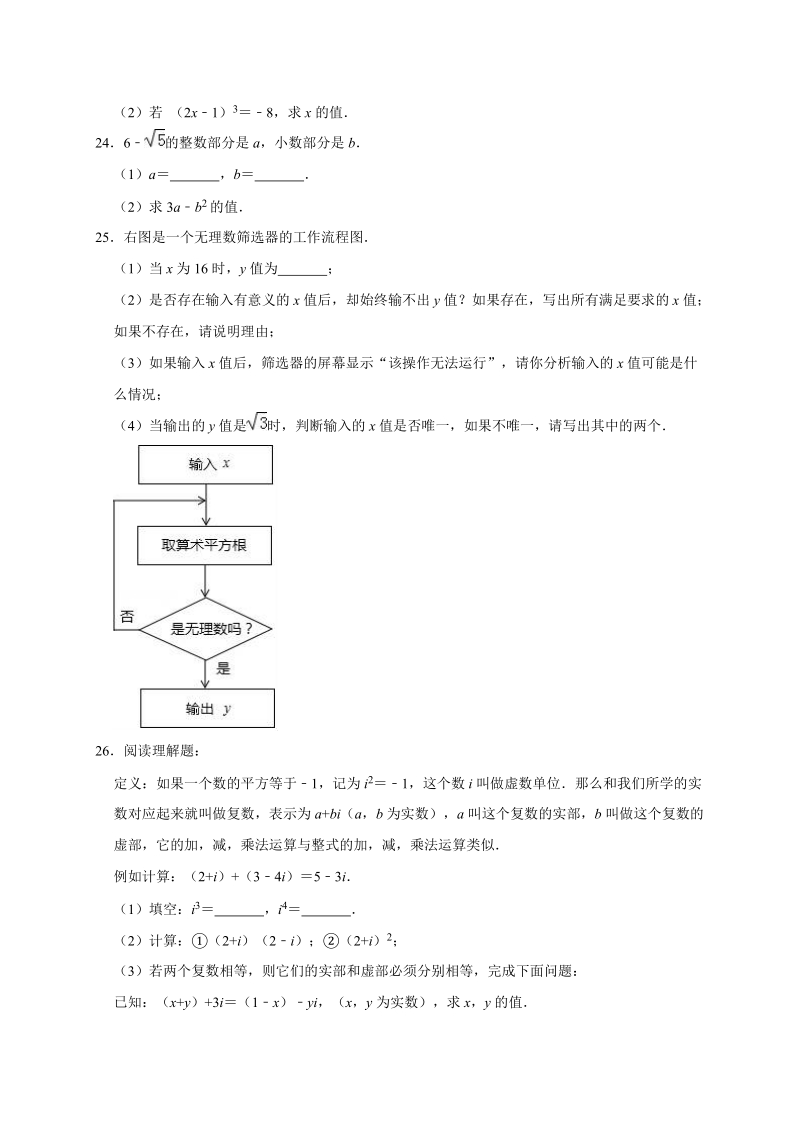
4、标出这组数对应的点的大致位置，并用“”把它们连接起来22已知 2（x1） 280，求 x 的值23（1）计算： ；（2）若 （2x1） 38，求 x 的值246 的整数部分是 a，小数部分是 b（1）a ，b （2）求 3ab 2 的值25右图是一个无理数筛选器的工作流程图（1）当 x 为 16 时，y 值为 ；（2）是否存在输入有意义的 x 值后，却始终输不出 y 值？如果存在，写出所有满足要求的 x 值；如果不存在，请说明理由；（3）如果输入 x 值后，筛选器的屏幕显示“该操作无法运行”，请你分析输入的 x 值可能是什么情况；（4）当输出的 y 值是 时，判断输入的 x 值是否唯一，如果不
5、唯一，请写出其中的两个26阅读理解题：定义：如果一个数的平方等于1，记为 i21，这个数 i 叫做虚数单位那么和我们所学的实数对应起来就叫做复数，表示为 a+bi（a，b 为实数），a 叫这个复数的实部，b 叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似例如计算：（2+i）+ （34i） 53i（1）填空：i 3 ，i 4 （2）计算：（2+i）（2i）；（2+i） 2；（3）若两个复数相等，则它们的实部和虚部必须分别相等，完成下面问题：已知：（x+y） +3i（1x）yi，（x，y 为实数），求 x，y 的值2019 年春人教新版七年级数学下册 第六章 实数 单元测试题
6、参考答案与试题解析一选择题（共 10 小题）164 的平方根是（ ）A8 B4 C8 D4【分析】根据平方根的定义回答即可【解答】解：（8） 264，64 的平方根是8故选：C【点评】本题主要考查的是平方根的定义和性质，掌握平方根的定义和性质是解题的关键2 的值是（ ）A4 B2 C4 D2【分析】如果一个正数 x 的平方等于 a，即 x2a，那么这个正数 x 叫做 a 的算术平方根【解答】解：4 216，16 的算术平方根是 4，即 4，故选：A【点评】本题主要考查了算术平方根，求一个非负数的算术平方根与求一个数的平方互为逆运算，在求一个非负数的算术平方根时，可以借助乘方运算来寻找3 的立方
7、根是（ ）A4 B2 C2 D8【分析】求出 后即可求出答案【解答】解： 8，8 的立方根为 2，故选：B【点评】本题考查立方根与平方根，解题的关键是正确理解立方根与平方根的定义，本题属于基础题型4下列说法正确的是（ ）A144 的平方根等于 12 B25 的算术平方根等于 5C 的平方根等于4 D 的等于3【分析】利用平方根、立方根定义判断即可【解答】解：A、144 的平方根是 12 和12，不符合题意；B、25 的算术平方根是 5，符合题意；C、 4，4 的平方根是 2 和2，不符合题意；D、 为 9 的立方根，不符合题意，故选：B【点评】此题考查了立方根，平方根，以及算术平方根，熟练掌握
8、各自的定义是解本题的关键5下列说法错误的是（ ）A5 是 25 的算术平方根B1 是 1 的一个平方根C9 的立方根是 3D0 的平方根与算术平方根都是 0【分析】利用算术平方根、平方根及立方根的定义分别判断后即可确定正确的选项【解答】解：A、5 是 25 的算术平方根，正确；B、1 是 1 的平方根，正确；C、9 的算术平方根是 3，故错误；D、0 的算术平方根和平方根都是 0，正确，故选：C【点评】本题考查了算术平方根、平方根及立方根的定义，熟练掌握它们的定义是解答本题的关键，难度较小6若将 ， ， 、 四个无理数表示在数轴上，其中能被如图所示的墨迹覆盖的数是（ ）A B C D【分析】先
9、估算出各数，再根据实数与数轴的关系即可得出结论【解答】解： 是负数，在原点的左侧，不符合题意；6 ，即 2 3，符合题意； ，即 3，在墨迹覆盖处的右边，不符合题意； ，即 4，在墨迹覆盖处的右边，不符合题意；故选：B【点评】本题考查的是实数与数轴，熟知实数与数轴上的点是一一对应关系是解答此题的关键7在数轴上，与表示 的点距离最近的整数点所表示的数是（ ）A1 B2 C3 D4【分析】利用平方根定义估算 的大小，即可得到结果【解答】解：466.25，2 2.5，则在数轴上，与表示 的点距离最近的整数点所表示的数是 2，故选：B【点评】此题考查了实数与数轴，以及算术平方根，熟练掌握各自的性质是解
10、本题的关键8如图，已知数轴上的点 A，B，0，C ，D，E 分别表示数3、2、0、1、2、3，则表示数1 的点 P 应落在线段（ ）AAB 上 BOC 上 CCD 上 DDE 上【分析】根据算出平方根的性质，被开方数越大，算数根就越大，得出 2 3，从而得出1 12，进而数轴的特点得出 P 点的位置【解答】解：2 3，1 12，表示 1 的点 P 应该落在线段 CD 上故选：C【点评】此题考查了估算无理数的大小，以及实数与数轴，弄清估算的方法是解本题的关键9在实数 0.23，4. ， ， ，0.3030030003（每两个 3 之间增加 1 个 0）中，无理数的个数是（ ）A1 个 B2 个
11、C3 个 D4 个【分析】无理数就是无限不循环小数理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称即有限小数和无限循环小数是有理数，而无限不循环小数是无理数由此即可判定选择项【解答】解：在所列的实数中，无理数有 ， ，0.3030030003（每两个 3 之间增加 1 个0）这 3 个，故选：C【点评】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：，2 等；开方开不尽的数；以及像 0.1010010001，等有这样规律的数10如果 x 的立方根是 3，那么 x 的值为（ ）A3 B9 C D27【分析】根据立方根的定义求出即可【解答】解：x 的立方根是 3，x
12、3 327，故选：D【点评】本题考查了立方根的定义，能熟记立方根的定义是解此题的关键二填空题（共 8 小题）11若一个正数的两个平方根分别为 1，1，则这个正数是 1 【分析】利用平方根定义计算即可得到结果【解答】解：若一个正数的两个平方根分别为 1，1，则这个正数是 1故答案为：1【点评】此题考查了平方根，熟练掌握平方根的定义是解本题的关键12根据如图所示的计算程序，若输入的 x 的值为 ，则输出的 y 的值为 1 【分析】先把 x 24，代入 x 中，计算即可【解答】解：当 x 2 时，y 21，故答案为：1【点评】本题考查了代数式求值和算术平方根，解答本题的关键就是弄清楚图中给出的计算程
13、序13（1.44） 2 的算术平方根为 1.44 ； 的平方根为 3 ； 0.2 【分析】根据算术平方根和平方根的定义逐一求解可得【解答】解：（1.44） 2 的算术平方根为 1.44；的平方根为3；0.2，故答案为：1.44、3、0.2【点评】本题主要考查算术平方根和平方根，解题的关键是掌握算术平方根和平方根的定义14已知一个正数的两个平方根分别为 2m6 和 3+m，则 m9 的立方根是 2 【分析】根据立方根与平方根的定义即可求出答案【解答】解：由题意可知：2m 6+3+m0，m1，m98，8 的立方根是2，故答案为：2【点评】本题考查立方根与平方根，解题的关键是熟练运用平方根与立方根，
14、本题属于基础题型15某个正数的平方根是 x 与 y，3x y 的立方根是 2，则这个正数是 4 【分析】由于一个正数有两个平方根，并且它们是一对相反数，由此即可列出方程 x+y0，再根据立方根的定义得出 3xy8，进而解方程组即可【解答】解：根据题意可得： ，解得： ，所以这个正数是 4，故答案为：4【点评】本题考查了平方根和立方根的概念注意一个正数有两个平方根，它们互为相反数16如果一个数的立方根是 4，那么这个数的算术平方根是 8 【分析】根据立方跟乘方运算，可得被开方数，根据开方运算，可得算术平方根【解答】解；4 364，8，故答案案为：8【点评】本题考查了立方根，先立方运算，再开平方运
15、算17数轴上到 这点距离为 的点表示的数是 0 或2 【分析】在数轴上表示 左右两边找出满足题意的数即可【解答】解：数轴上到 这点距离为 的点表示的数是 0 或2 ，故答案为：0 或2【点评】此题考查了实数与数轴，解题关键是求数轴上两点间的距离应让较大的数减去较小的数即可18写一个比 4 小的无理数 【分析】找出一个小于 4 的无理数即可【解答】解：比 4 小的无理数可以是 ，故答案为：【点评】此题考查了实数大小比较，以及无理数，熟练掌握无理数的定义是解本题的关键三解答题（共 8 小题）19计算： + +|1 |【分析】根据实数的运算即可求出答案【解答】解：原式3 +2 2+ 14 1【点评】
16、本题考查实数的运算，解题的关键是熟练运用实数的运算法则，本题属于基础题型20已知 A 是 m+n+4 的算术平方根，B 是 m+2n 的立方根，求 BA 的立方根【分析】利用算术平方根，立方根的定义求出 m 与 n 的值，进而确定出 A 与 B，即可求出BA 的立方根【解答】解：根据题意得： ，解得： ，A 2，B 1，则 BA123，3 的立方根为 【点评】此题考查了立方根，以及算术平方根，熟练掌握各自的定义是解本题的关键21已知下列一组数：， （1）将这组数分类填入相应的大括号内1 分数集合： 3.1415926， ， ；2 无理数集合： ；3 非负数集合： ，0，3.1415926 ，
17、， （2）在数轴上标出这组数对应的点的大致位置，并用“”把它们连接起来【分析】（1）根据分数的定义，可得答案，无理数是无限不循小数，大于或等于零的数是非负数，可得答案；（2）根据数轴上的点表示的数右边的总比左边的大，可得答案【解答】解：（1）分数集合3.1415926， ， ；无理数集合 ；非负数集合 ，0，3.1415926， ， 故答案为：3.1415926， ， ； ； ，0，3.1415926， ， （2）如图 ，3 0 3.1415926 【点评】本题考查了实数与数轴，利用数轴上的点表示的数右边的总比左边的大是解题关键22已知 2（x1） 280，求 x 的值【分析】已知方程整理后，
18、利用平方根定义开方即可求出解【解答】解：方程整理得：（x1） 24，开方得：x12 或 x12，解得：x3 或 x1【点评】此题考查了平方根，熟练掌握平方根定义是解本题的关键23（1）计算： ；（2）若 （2x1） 38，求 x 的值【分析】（1）根据实数的运算法则即可求出答案（2）根据立方根的定义即可求出答案【解答】解：（1）原式5+（3）（4 ）24+2+ ；（2）由题意可知：2x12，x 【点评】本题考查学生的运算能力，解题的关键是熟练运用运算法则，本题属于基础题型246 的整数部分是 a，小数部分是 b（1）a 3 ，b 3 （2）求 3ab 2 的值【分析】（1）先估算出 的大小，然
19、后可求得 6 的大致范围，可得到 a、b 的值；（2）将 a、b 的值代入计算即可求解【解答】解：（1）4 9，2 32 3626 63，46 3a3，b3 （2）3ab 233（3 ） 29（96 +5） 6 5【点评】本题主要考查的是估算无理数的大小，熟练掌握相关知识是解题的关键25右图是一个无理数筛选器的工作流程图（1）当 x 为 16 时，y 值为 ；（2）是否存在输入有意义的 x 值后，却始终输不出 y 值？如果存在，写出所有满足要求的 x 值；如果不存在，请说明理由；（3）如果输入 x 值后，筛选器的屏幕显示“该操作无法运行”，请你分析输入的 x 值可能是什么情况；（4）当输出的
20、y 值是 时，判断输入的 x 值是否唯一，如果不唯一，请写出其中的两个【分析】（1）根据运算规则即可求解；（2）根据 0 的算术平方根是 0，即可判断；（3）根据二次根式有意义的条件，被开方数是非负数即可求解；（4）根据运算法则，进行逆运算即可求得无数个满足条件的数【解答】解：（1）当 x16 时， 4， 2，则 y ；故答案是： （2）当 x0，1 时，始终输不出 y 值因为 0，1 的算术平方根是 0，1，一定是有理数；（3）当 x0 时，导致开平方运算无法进行；（4）x 的值不唯一x 3 或 x9【点评】本题考查了二次根式有意义的条件，正确理解给出的运算方法是关键26阅读理解题：定义：如
21、果一个数的平方等于1，记为 i21，这个数 i 叫做虚数单位那么和我们所学的实数对应起来就叫做复数，表示为 a+bi（a，b 为实数），a 叫这个复数的实部，b 叫做这个复数的虚部，它的加，减，乘法运算与整式的加，减，乘法运算类似例如计算：（2+i）+ （34i） 53i（1）填空：i 3 i ，i 4 1 （2）计算：（2+i）（2i）；（2+i） 2；（3）若两个复数相等，则它们的实部和虚部必须分别相等，完成下面问题：已知：（x+y） +3i（1x）yi，（x，y 为实数），求 x，y 的值【分析】（1）根据阅读材料中的方法计算即可求出值；（2）各式利用平方差公式，以及完全平方公式计算即可求出值；（3）根据实数部分与虚数部分相等列出方程，求出方程的解即可得到 x 与 y 的值【解答】解：（1）i 3i，i 41；故答案为：i；1；（2） 原式 4i 24+15；原式4+4 i+i23+4i；（3）由已知等式得：x+y 1x ，y3，解得：x2，y3【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键
