2019年北京中考数学习题精选：二次函数在实际生活中应用

《2019年北京中考数学习题精选：二次函数在实际生活中应用》由会员分享，可在线阅读，更多相关《2019年北京中考数学习题精选：二次函数在实际生活中应用（6页珍藏版）》请在七七文库上搜索。

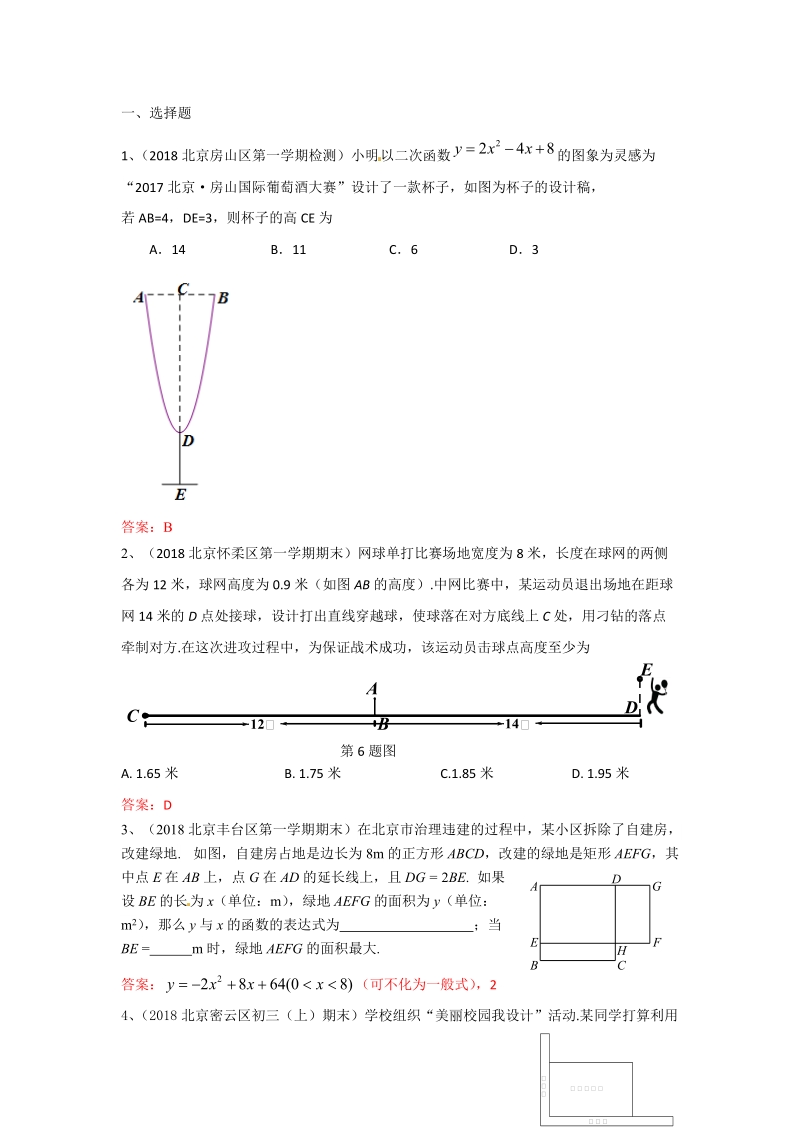
1、一、选择题1、 （ 2018 北京房山区第一学期检测）小明 以二次函数 的图象为灵感为248yx“2017 北京房山国际葡萄酒大赛”设计了一款杯子，如图为杯子的设计稿，若 AB=4，DE=3，则杯子的高 CE 为A14 B11 C6 D3答案：B2、（2018 北京怀柔区第一学期期末）网球单打比赛场地宽度为 8 米，长度在球网的两侧各为 12 米，球网高度为 0.9 米（如图 AB 的高度）.中网比赛中，某运动员退出场地在距球网 14 米的 D 点处接球，设计打出直线穿越球，使球落在对方底线上 C 处，用刁钻的落点牵制对方.在这次进攻过程中，为保证战术成功，该运动员击球点高度至少为A. 1.6

2、5 米 B. 1.75 米 C.1.85 米 D. 1.95 米答案：D3、（2018 北京丰台区第一学期期末）在北京市治理违建的过程中，某小区拆除了自建房，改建绿地. 如图， 自建房占地是边长为 8m 的正方形 ABCD，改建的绿地是矩形 AEFG，其中点 E 在 AB 上，点 G 在 AD 的延长线上，且 DG = 2BE. 如果设 BE 的长 为 x（单位：m） ，绿地 AEFG 的面积为 y（单位：m2） ，那么 y 与 x 的函数的表达式为 ；当BE = m 时，绿地 AEFG 的面积最大.答案： （可不化为一般式） ，22864(08)x4、 （2018 北京密云区初三（上）期末）

3、学校组织“美丽校园我设计”活动.某同学打算利用E DGFHA CB第 6 题图B米 1412 EAC D化化化学校文化墙的墙角建一个矩形植物园.其中矩形植物园的两邻边之和为 4m，设矩形的一边长为 m，矩形的面积为 m2.则函数 的表达式为_，该矩形植物园的最大xyy面积是_ _ m2.答案： ，4 ()y5、（2018 北京顺义区初三上学期期末）如图，利用成直角的墙角（墙足够长） ，用 10m长的栅栏围成一个矩形的小花园，花园的面积 S（m 2）与它一边长 a（m）的函数关系式是 ，面积 S 的最大值是 答案： 20Sa6、（2018 年北京昌平区第一学期期末质量抽测）如图，是一 座古拱桥的

4、截面图，拱桥桥洞的上沿是抛物线形状，当水面的宽度为 10m 时，桥洞与水面 的最大距离是 5m（1）经过讨论，同学们得出三种建立平面直角坐标系的方案（如下图），你选择的方案是_(填方案一，方案二，或方 案三) ，则 B 点坐标是_，求出你所选方案中的抛物线的表达式；（2）因为上游水库泄洪，水面宽度变为 6m，求水面上涨的高度 解：方案 1：（1）点 B 的坐标为（ 5,0） 1 分 设抛物线的解析式为： 2 分(5)yax由题意可以得到抛物线的顶点为（0,5） ，代入解析式可得： 15a抛物线的解析式为： 3 分1(5)yx 5m10mxy xy xyAOB 化 2 OBA化 3BOA化 1（

5、2 ）由题意：把 代入 解得： =3.2 5 分3x1(5)yx165y水面上涨的高度为 3.2m 6 分方案 2：（1）点 B 的坐标为（ 10,0） 1 分 设抛物线的解析式为： 2 分(10)yax由题意可以得到抛物线的顶点为（5,5） ，代入解析式可得： 15a抛物线的解析式为： 3 分(10)5yx（2）由题意：把 代入 解得： =3.2 5 分2x165y水面上涨的高度为 3.2m 6 分方案 3：（1）点 B 的坐标为（ 5, ） 1 分 5由题意可以得到抛物线的顶点为（0,0）设抛物线的解析式为： 2 分2yax把点 B 的坐标（5, ） ，代入解析式可得： 515a抛物线的解

6、析式为： 3 分21yx（2）由题意：把 代入 解得： = 5 分3x595y1.8水面上涨的高度为 3.2m 6 分1.87、 （2018 北京朝阳区第一学期期末检测）图中所示的抛物线形拱桥，当拱顶离水面 4m 时，水面宽 8m. 水面上升 3 米，水面宽度减少多少？下面给出了解决这个问题的两种方法. 方法一 如图 1，以上升前的水面所在直线与抛物线左侧交点为原点，以上升前的水面所在直线为 x 轴，建立平面直角坐标系 xOy，这时这条抛物线所表示的二次函数的表达式为 ；当 y3 时，求出此时自变量 x 的取值，即可解决这个问题. 图 1方法二 如图 2，以抛物线顶点为原点，以抛物线的对称轴为

7、 y 轴，建立平面直角坐标系 xOy，这时这条抛物线所表示的二次函数的表达式为 ；当 y 时，求出此时自变量 x 的取值，即可解决这个问题.图 2解：方法一 ； 2 分y241方法二 ； 4 分x1. 5 分8、 （ 2018 北京东城第一学期期末） 如图，以 40 m/s 的速度将小球沿与地面成 30角的方向击出时，小球的飞行路线是一条抛物线如果不考虑空气阻力，小球的飞行高度h（单位：m）与飞行时间 t（单位：s）之间具有函数关系 205h（1 ）小球飞行时间是多少时，小球最高？最大高度是多少？（2 ）小球飞行时间 t 在什么范围时，飞行高度不低于 15 m? 答案：23解： 22050ht

8、t（1）当 t=2 时，小球最高，最大高度是 20 m; 3 分（2）令 =15，22tt解得 ， 1t23当 时，小球飞行高度不低于 15 m 5 分 9、 （ 2018 北京丰台区第一学期期末）如图，人工喷泉有一个竖直的喷水枪 AB，喷水口 A距地面 2m，喷出水流的运动路线是抛物线 . 如果水流的最高点 P 到喷水枪 AB 所在直线的距离为 1m，且到地面的距离为 3.6m，求水流的落地点 C 到水枪底部 B 的距离 .解：建立平面直角坐标系，如图.于是抛物线的表达式可以设为2yaxhkPCBA根据题意，得出 A，P 两点的坐标分别为 A（0 ，2），P（1，3.6）. 2 分点 P 为

9、抛物线顶点， .136hk，点 A 在抛物线上， ， 2a13 分它的表达式为. 4 分21.63yx当点 C 的纵坐标 y=0 时，有.2.=0（舍去）， .15x25xBC=2.5. 水流的落地点 C 到水枪底部 B 的距离为 2.5m. 5 分10.（2018 北京通州区第一学期期末）如图，李师傅想用长为 80 米的栅栏，再借助教学楼的外墙围成一个矩形的活动区 . 已知教学楼外墙长 50 米，设矩形 的边ADABCD米，面积为 平方米.xABS（1）请写出活动区面积 与 之间的关系式，并指出 的取值范围；xx（2）当 为多少米时，活动 区的面积最大？最大面积是多少？答案：11.（2018 北京西城区第一学期期末）运动员将小球沿与地面成一定角度的方向击出，在不考虑空气阻力的条件下，小球的飞行高度 h（m）与它的飞行时间 t（s）满足二次函数关系，t 与 h 的几组对应值如下表所示Oy xPCAt（s） 0 0.5 1 1.5 2 h（m） 0 8.75 15 18 .75 20 （1）求 h 与 t 之间的函数关系式（不要求写 t 的取值范围） ；（2）求小球飞行 3 s 时的高度；（3）问：小球的飞行高度能否达到 22 m？请说明理由