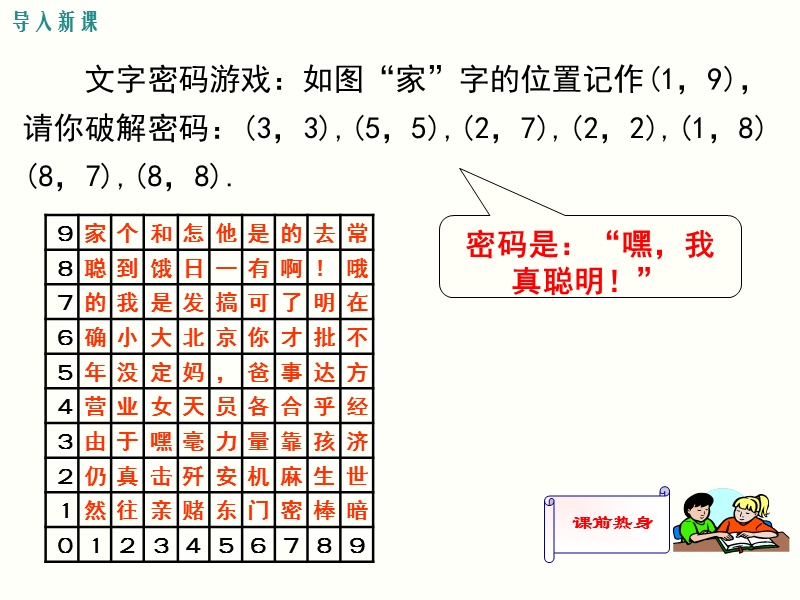
1、,导入新课,讲授新课,当堂练习,课堂小结,19.2 平面直角坐标系,第十九章 平面直角坐标系,第1课时 平面直角坐标系,学习目标,1.理解平面直角坐标系以及横轴、纵轴、原点、坐标 等概念；（重点） 2.能在给定的直角坐标系中，由点的位置写出它的坐 标.（难点）,导入新课,文字密码游戏：如图“家”字的位置记作(1，9)，请你破解密码：(3，3),(5，5),(2，7),(2，2),(1，8) (8，7),(8，8).,密码是：“嘿，我真聪明！”,导入新课,在平面内，确定物体位置方式主要有两种：,一般记作（a ，b）,(横 纵）,(方位角距离）,在平面内，确定物体位置,需 _ 数据,两个,思考：（
2、a ，b）从何而来呢？,讲授新课,问题：如图是某城市旅游 景点的示意图：,(1) 你是怎样确定各个景点位置的？,（3，1）,（2，1）,（2，1）,（1，3）,（4，4）,1.你是怎样确定各个旅游景点的位置的？,2.“大成殿”在“中心广场”的西南各多少个小格？“碑林”在广场的东北各多少格？,3.如果中心广场为（0,0）你能表示出其他景点的位置么？,小丽能根据小明的提示从左图中找出图书馆的位置吗？,周末小明和小丽约好一起去图书馆学习.小明告诉小丽，图书馆在中山北路西边50米，人民西路北边30米的位置.,找一找,想一想,4.如果小明只说在“中山北路西边50米”，或只说在“人民西路北边30米”，你能
3、找到吗？,1.小明是怎样描述图书馆的位置的？,2.小明可以省去“西边”和“北边”这几个字吗？,3.如果小明说图书馆在“中山北路西边、人民西路北边”，你能找到吗？,若将中山路与人民路看着两条互相垂直的数轴，十字路口为它们的公共原点，这样就形成了一个平面直角坐标系.,x,y,o,30,20,10,20,10,-10,-20,-30,-40,-20,-50,-10,-70,-60,-50,-40,-30,-80,（-50,北,西,30）,人民路,中山路,O,y,在平面内画两条互相垂直的数轴,构成平面直角坐标系.,1,2,3,4,5,-4,-3,-2,-1,x,竖直的叫y轴或纵轴； y轴取向上为正方向
4、,水平的叫x轴或横轴； x轴取向右为正方向,x轴与y轴的交点叫平面直角坐标系的原点.,概念学习,思考：如何在平面直角坐标系中表示点呢？,x,O,练一练：下面四个图形中，是平面直角坐标系的是（ ）,x,x,y,（A）,3 2 1 -1 -2 -3,x,y,（B）,2 1-1 -2,O,D,这样P点的横坐标是-2，纵坐标是3，规定把横坐标写在前，纵坐标在后，记作：P(-2，3) P(-2，3)就叫做点P在平面直角坐标系中的坐标，简称点P的坐标.,思考：如图点P如何表示呢？,后由P点向y轴画垂线，垂足N在y轴上的坐标是3, 称为P点的纵坐标.,先由P点向x轴画垂线，垂足M在x轴上的坐标是是-2,称为
5、P点的横坐标.,P,N,M,1,1,-1,-2,-3,-4,2,3,2,3,4,5,4,-1,-2,-3,-4,-5,O,（，）,x,y,1. 找出点的坐标.,(1)过点作x轴的垂线，垂足在x轴上对应的数是； (2)过点作y轴的垂线，垂足在y轴上对应的数是；点的坐标为（，）,试一试,2. 在平面直角坐标系中 找点A(3,-2),由坐标找点的方法：(1)先找到表示横坐标与纵坐标的点；(2)然后过这两点分别作x轴与y轴的垂线；(3)垂线的交点就是该坐标对应的点.,A,典例精析,A,B,C,E,F,D,例：写出下图中的多边形ABCDEF各个顶点的坐标.,1,2,3,4,-1,-2,1,2,3,-1,
6、-2,-3,【答案】 A（-2，0） B（0，-3） C（3，-3） D（4，0） E（3，3） F（0，3）,y,O,x,在直角坐标系中描出下列各点： A（4，3）， B（-2，3）， C（-4，-1）， D（2，-2）.,x,y,练一练,思考：坐标平面内的点与有序数对(坐标)是什么关系?,类似数轴上的点与实数是一一对应的.我们可以得出： 对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标）和它对应； 反过来，对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点）和它对应. 也就是说，坐标平面内的点与有序实数对是一一对应的.,当堂练习,
7、1.如图，点A的坐标为( ) A. ( -2，3) B. ( 2，-3) C . ( -2，-3) D . ( 2，3),x,y,O,1,2,3,-3,-2,-1,1,2,-1,-2,A,A,2.如图，点A的坐标为 ， 点B的坐标为 .,x,y,O,1,2,3,-3,-2,-1,1,2,-1,-2,A,B,(-2,0),(0,-2),3.某邮递员投递区域街道如图所示.现在，他要把一封邮件从邮政局所在地O处尽快送到A地.他选择的一条路径是,（0，0）（0，3） （4，3） （4，8） （7，8） （1）用彩笔在图中标出邮递员走的这条路径.（2）用坐标写出由点O到点A的其他最短的路径.,（1）图中
8、黄线所示,（2）路径1：图中红线所示，坐标为（0，0） （4，0） （4，3） （4，8） （7，8）；,路径2：图中蓝线所示，坐标为（0，0） （4，0） （7，0） （7，8）.,（2）用坐标写出由点O到点A的其他最短的路径.,A,B,C,D,E,4.下图是某植物园的平面示意图，A是大门，B、C、D、E分别表示梅、兰、菊、竹四个花圃. 请建立平面直角坐标系，写出各花圃的坐标.,hm,hm,解：以A点为原点，以水平方向为坐标轴建立直角坐标系，则B（2，3），C（5，10）， D（8，8），E（11，9）.,课堂小结,平面直角坐标系,平面直角坐标系的概念,在平面直角坐标系中描点,表示平面直角坐标系中点的坐标,
