1、专题二 阅读理解专题【考纲与命题规律】考纲要求 阅读理解类问题是近几年中考的新题型，主要目的是考查学生通过阅读，学习新的知识、感悟数学思想和方法它能较好地体现知识的形式、发展的过程要求学生理解问题，并对其本质进行概括及迁移发展命题规律 阅读题共有三类：(1)图文型(用文字和图形相结合展示条件和问题)；(2)表文型(用文字和表格相结合的形式展示条件和问题)；(3)改错型无论哪种类型，其解题步骤分为三步：(1)快速阅读，把握大意；(2)仔细阅读，提炼信息或方法；(3)总结方法，建立解决问题的模式【课堂精讲】例 1 阅读例题，模拟例题解方程解方程 x2| x1|10.解：(1)当 x10 即 x1
2、时，原方程可化为： x2 x110 即 x2 x20，解得 x11， x22(不合题意，舍去)(2)当 x10 即 x1 时，原方程可化为： x2( x1)10 即 x2 x0，解得x30， x41(不合题意，舍去)综合(1)、(2)可知原方程的根是 x11， x20.请 你模拟以上例题解方程： x2| x3|90.解析：(1)当 x30 时，即 x3 时原方程可化为： x2 x60.解得 x12， x23.(2)当 x30 时，即 x3 时原方程可化为： x2 x120.解得 x33， x44.经检验， x33， x44 都不符合题意，舍去综合(1)、(2)可知原方程的根为 x12， x23
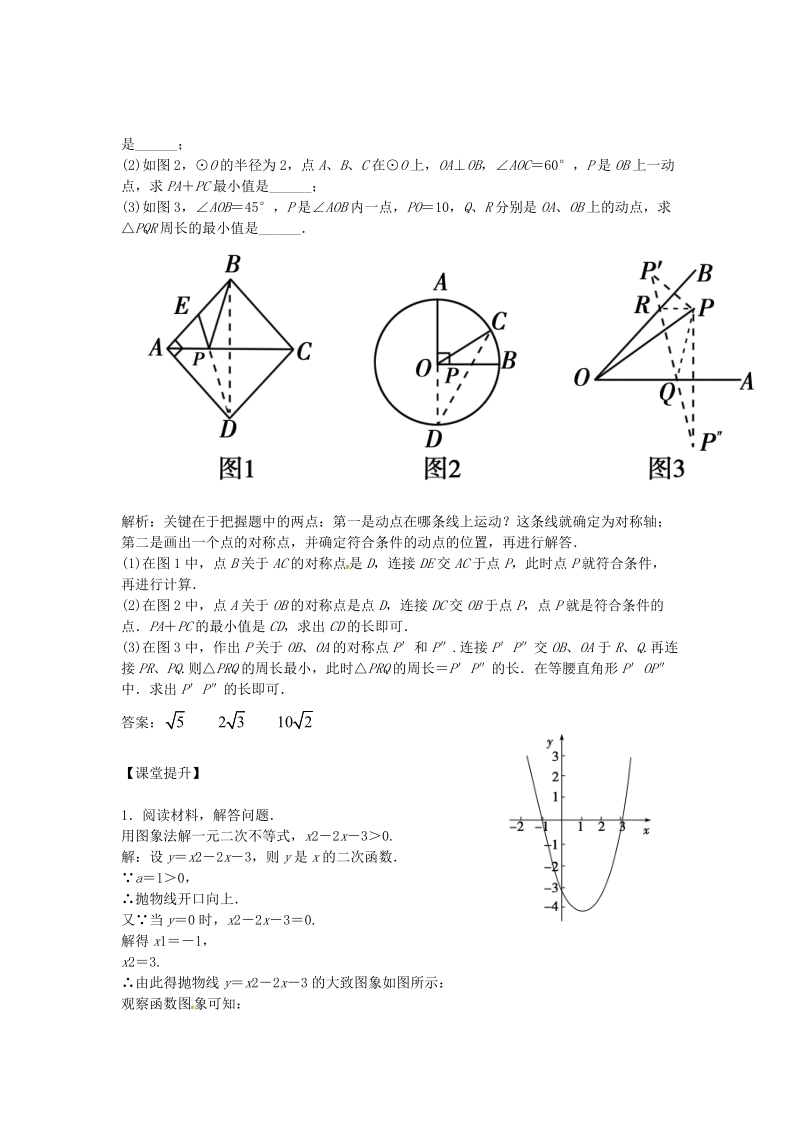
3、.点评：解决这类题的策略是先理解例题的思想方法，再把这种思想方法迁移到问题中从而得到解决例 2 条件：如下图， A、 B 是直线 l 同旁的两个定点问题：在直线 l 上确定一点 P，使PA PB 的值最小方法：作点 A 关于直线 l 的对称点 A，连接 A B 交 l 于点 P，则PA PB A B 的值最小模型应用：(1)如图 1，正方形 ABCD 边长为 2， E 为 AB 的中点， P 是 AC 上一动点则 PB PE 的最小值是_；(2)如图 2， O 的半径为 2，点 A、 B、 C 在 O 上， OA OB， AOC60， P 是 OB 上一动点，求 PA PC 最小值是_；(3)
4、如图 3， AOB45， P 是 AOB 内一点， PO10， Q、 R 分别是 OA、 OB 上的动点，求 PQR 周长的最小值是_解析：关键在于把握题中的两点：第一是动点在哪条线上运动？这条线就确定为对称轴；第二是画出一个点的对称点，并确定符合条件的动点的位置，再进行解答(1)在图 1 中，点 B 关于 AC 的对称点 是 D，连接 DE 交 AC 于点 P，此时点 P 就符合条件，再进行计算(2)在图 2 中，点 A 关于 OB 的对称点是点 D，连接 DC 交 OB 于点 P，点 P 就是符合条件的点 PA PC 的最小值是 CD，求出 CD 的长即可(3)在图 3 中，作出 P 关于
5、 OB、 OA 的对称点 P和 P.连接 P P交 OB、 OA 于 R、 Q.再连接 PR、 PQ.则 PRQ 的周长最小，此时 PRQ 的周长 P P的长在等腰直角形 P OP中求出 P P的长即可答案： 5 2 10【课堂提升】1阅读材料，解答问题用图象法解一元二次不等式， x22 x30.解：设 y x22 x3，则 y 是 x 的二次函数 a10，抛物线开口向上又当 y0 时， x22 x30.解得 x11，x23.由此得抛物线 y x22 x3 的大致图象如图所示：观察函数图 象可知：当 x1 或 x3 时， y0. x22 x30 的解集是：x1 或 x3.(1)观察图象，直接写
6、出一元二次不等式：x 2-2x-30 的解集是_；(2)仿照上例，用图象法解一元二次不等式：x 2-5x+60 的解集.2. 阅读下列材料：解答“已知 x y=2，且 x1， y0，试确定 x+y 的取值范围”有如下解法：解 x y=2， x=y+2又 x1， y+21 y1又 y0，1 y0 同理得：1 x2 由+得1+1 y+x0+2来源:学科网 x+y 的取值范围是 0 x+y2请按照上述方法，完成下列问题：（1）已知 x y=3，且 x2， y1，则 x+y 的取值范围是 （2）已知 y1， x1，若 x y=a 成立，求 x+y 的取值范围（结果用含 a 的式子表示）3.如果三角形满
7、足一个角 是另一个角的 3 倍，那么我们称这个三角形为“智慧三角形”下列各组数据中，能作为一个智慧三角形三边长的一组是（ ）A 1，2，3 B 1，1， C 1，1， D 1，2，4阅读理解：我们知道，任意两点关于它们所连线段的中点成中心对称，在平面直角坐标中，任意两点 P(x1， y1)， Q(x2， y2)的对称中心的坐标为( 12x ， 12y )(1)如图，在平面直角坐标系中，若 点 P1(0，1)， P2(2,3)的对称中心是点 A，则点 A 的坐标为_；(2)另取两点 B(1.6,2.1)， C(1,0)有一电子青蛙从点 P1 处开始依次关于点 A， B， C作循环对称跳动，即第一
8、次跳到点 P1 关于点 A 的对称点 P2 处，接着跳到点 P2 关于点 B 的对称点 P3 处，第三次再跳到点 P3 关于点 C 的对称点 P4 处，第四次再跳到点 P4 关于点 A的对称点 P5 处，则点 P3， P8 的坐标分别为_、_；(3)求出点 P2012 的坐标，并直接写出在 x 轴上与点 P2012、点 C 构成等腰三角形的点的坐标【高效作业本】专题二 阅读理解专题1.如图，已知正方形 ABCD，顶点 A(1，3)、 B(1,1)、 C(3,1)规定“把正方形 ABCD 先沿 x轴翻折，再向左平移 1 个单位”为一次变换如此这样，连续经过 2014 次变换后，正方形ABCD 的
9、对角线交点 M 的坐标变为( )A(2012,2) B （一 2012，一 2） C. (2013,2) D. (2013,2)2.定义新运算：对于任意实数 a， b都有 a b=ab a b+1，等式右边是通常的加法、减法及乘法运算，例如：24=2424+1=86+1=3，请根据上述知识解决问题：若 3 x 的值大于 5而小于 9，求 x 的取值范围3(1)阅读：探究下表中的奥秘，并完成填空：一元二次方程 两个根 二次三项式因式分解x22 x10 x11， x21 x22 x1( x1)( x1)x23 x20 x11， x22 x23 x2( x1)( x2)3x2 x20 x1 ， x2
10、1 3x2 x23( x )( x1)2x25 x20 x1_， x2_ 2x25 x22( x )( x2)4x213 x30 x1_， x2_ 4x213 x34( x_)( x_)(2)若关于 x 的方程 ax2 bx c0 的两个根为 x1， x2，将你发现的结论一般化，并写出来4阅读下面的例题：解方程 x2| x|20解：(1)当 x0 时，原方程化为 x2 x20解得 x12， x21(不合题意，舍去)(2)当 x0 时，原方程化为 x2 x20，解得 x11(不合题意，舍去)， x22所以原方程的解是x12， x22请参照例题，解方程 ： x2| x3|30.来源:学科网【答案】
11、专题二 阅读理解专题答案1.分析：（1）观察图象即可写出一元二次不等式：x 2-2x-30 的解集；（2）先设函数解析式，根据 a 的值确定抛物线的开口向上，再找出抛物线与 x 轴相交的两点，就可以画出抛物线，根据 y0 确定一元二次不等式 x2-2x-30 的解集解：（1）观察图象，可得一元二次不等式 x2-2x-3 0 的解集是：-1x3（2）设 y=x2-5x+6，则 y 是 x 的二次函数a=10，抛物线开口向上又当 y=0 时，x 2-5x+6=0，解得 x1=2，x 2=3由此得抛物线 y=x2-5x+6 的大致图象如图所示观察函数图象可知：当 2x3 时，y0x 2-5x+60
12、的解集是：2x3点评：本题主要考查在直角坐标系中利用二次函数图象解不等式，可作图利用交点直观求解集2.解：（1）xy =3，x=y +3，又x2，y+32，y1又y1，1y1，同理得：2x4，由+得1+2y+x 1+4x+y 的取值范围是 1x+y 5；（2）xy=a，来源:学科网 ZXXKx=y +a，又x1，y+a1，ya1，又y1，1ya1，同理得：a+1x1，由+得 1+a+1y+x a1+（1），x+y 的取值范围是 a+2x+ya2本题考查了一元一次不等式组的应用，解答本题的关键是仔细阅读材料，理解解题过程，难度一般来源:Zxxk.Com3.分析 A、根据三角形三边关系可知，不能构
13、成三角形，依此即可作出判定；B、根据勾股定理的逆定理可知是等腰直角三角形，依此即可作出判定；C、解直角三角形可知是顶角 120，底角 30的等腰三角形，依此即可作出判定；D、解直角三角形可知是三个角分别是 90，60 ，30的直角三角形，依此即可作出判定解：A、1+2=3，不能构成三角形，故选项错误；B、1 2+12=（ ） 2，是等腰直角三角形，故选项错误；C、底边上的高是 = ，可知是顶角 120，底角 30的等腰三角形，故选项错误；D、解直角三角形可知是三个角分别是 90，60 ，30的直角三角形，其中 9030=3，符合“智慧三角形” 的定义，故选 项正确故选：D点评： 考查了解直角三
14、角形，涉及三角形三边关系，勾股定理的逆定理，等腰直角三角形的判定，“智慧三角形” 的概念4.(1)(1,1)；(2)( 5.2,1.2)；(2,3)(提示：P1(0，1) ，P2(2,3)，P3(5.2,1.2)，P4(3.2，1.2) ，P 5(1.2,3.2)，P6(2,1)，P7(0，1) ，P8(2,3)(3)P 1(0，1)P 2(2,3)P 3(5.2,1.2)P4(3.2，1.2)P5(1.2,3. 2)P6( 2,1)P7(0，1) P8(2,3)，P7 的坐标和 P1 的坐标相同，P8 的坐标和 P2 的坐标相同，即坐标以 6 为周期循环2012 63352.P2012 的坐
15、标与 P2 的坐标相同，即 P2012(2,3)；在 x 轴上与点 P2012，点 C 构成等腰三角形的点的坐标为(3 1,0)，(2,0)，(3 1,0)，(5,0)【高效作业本】1.分析：首先求出正方形对角线交点坐标分别是（2，2） ，然后根据题意求得第 1 次、2 次、3 次变换后的点 M的对应 点的坐标，即可得规律解答：正方形 ABCD，点 A(1，3)、 B(1,1)、 C(3,1) M 的坐标变为(2,2)根据题意得：第 1 次变换后的点 M 的对应点的坐标为（2 1， 2） ，即（1， 2） ，第 2 次变换后的点 M 的对应点的坐标为：（2 2，2） ，即（0，2） ，第 3
16、次变换后的点 M 的对应点的坐标为（2 3， 2） ，即（ 1， 2） ，第 2014 次变换后的点 M 的对应点的为坐标为（2 2014， 2） ，即（ 2012， 2）故答案为 A点评：此题考查了对称与平移的性质此题难度较大，属于规律性题目，注意得到规律：第 n 次变换后的点 M 的对应点的坐标为：当 n 为奇数时为（2 n， 2） ，当 n 为偶数时为（2 n，2）是解此题的关键2.分析：首先根据运算的定义化简 3x，则可以得到关于 x 的不等式组，即可求解解答：3x=3x3x+1=2x2，根据题意得： ，解得：x 点评：本题考查了一元一次不等式组的解法，正确理解运算的定义是关键3.(1) 2 3 312 14 14(2)ax2bxca(xx1)(xx2)4.解析：(1)当 x3 3，原方程为 x2( x3)30 x3不符合题意，都舍去(2)当 x30 时，即 x3，原方程化为x2( x3)30解得 x2( x3)0解得 x13 或 x22( 都符合题意)所以原方程的解是 x13 或 x22.答案： x3 或 x2
