1、武汉市 2019 届高中毕业生二月调研测试理科数学一、选择题：本题共 12 小题，每小题 5 分，共 60 分在每小题给出的四个选项中，只有一项是符合题目要求的1已知复数 满足 ，则 （ ）z(34i)7izzA B C D i11i1i答案：B考点：复数的运算。解析： 7i(i)3425i34iz2已知集合 ，则 （ ）20,|0AxBx ABA B C D (0,4,2(0,2答案：A考点：集合的运算，一元二次不等式，绝对值不等式。解析：因为 ，|0x所以，当 x0 时， 240,Axx 即 ，选 A。(,4B3已知等差数列 的前 项和为 ，若 ，则等差数列 的公差 （ nanS152,9
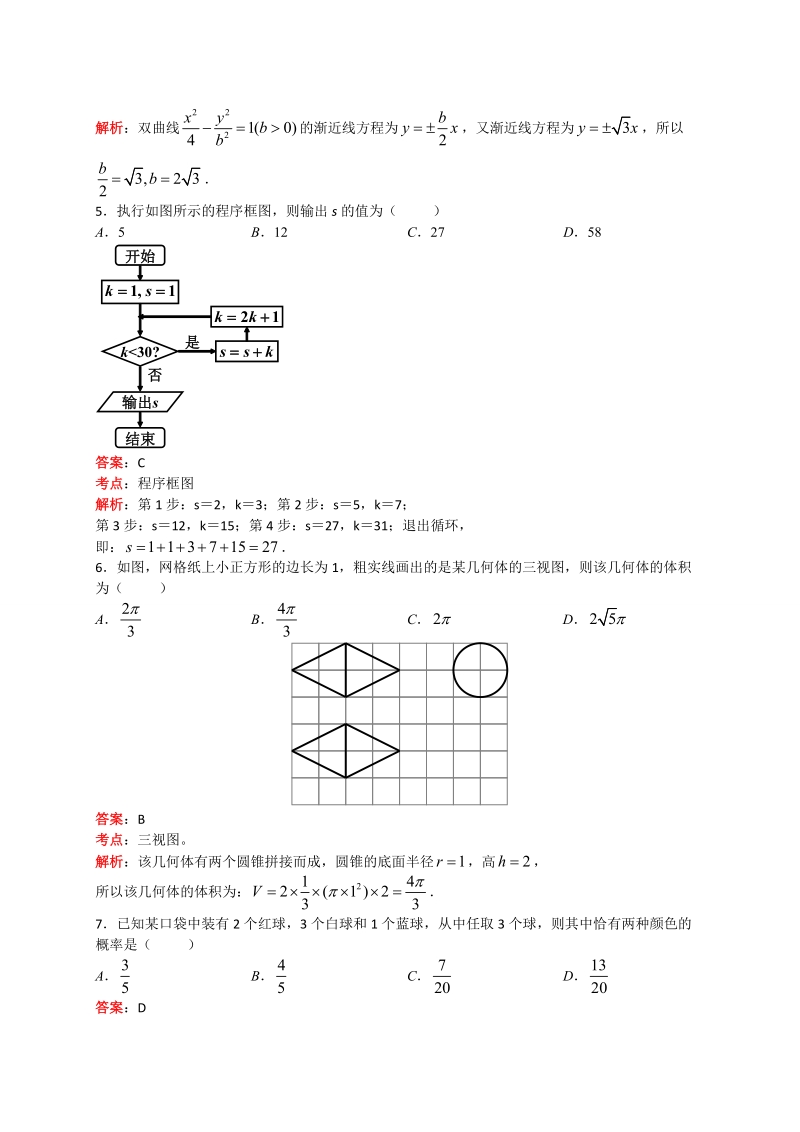
2、aSnad）A2 B C3 D432答案：C考点：等差数列的前 n 项和公式。解析： ，解得 5146019Sadd4已知双曲线 的渐近线方程为 ，则 （ ）2()xyb30xybA B C D12332答案：A考点：双曲线的性质。解析：双曲线 的渐近线方程为 ，又渐近线方程为 ，所以21(0)4xyb2byx3yx3,2b5执行如图所示的程序框图，则输出 s 的值为（ ）A5 B12 C27 D58开 始1,ksk30?输 出 s结 束 21ks是否答案：C考点：程序框图解析：第 1 步：s2，k3；第 2 步：s5，k7；第 3 步：s 12，k15；第 4 步：s 27，k31；退出循环
3、，即： 76如图，网格纸上小正方形的边长为 1，粗实线画出的是某几何体的三视图，则该几何体的体积为（ ）A B C D 233225答案：B考点：三视图。解析：该几何体有两个圆锥拼接而成，圆锥的底面半径 ，高 ，1r2h所以该几何体的体积为： 214()33V7已知某口袋中装有 2 个红球，3 个白球和 1 个蓝球，从中任取 3 个球，则其中恰有两种颜色的概率是（ ）A B C D 35457201320答案：D考点：古典概型，排列组合。解析：方法一：设 2 个红球编号为：1、2；3 个白球编号为：A、B、C；1 个蓝球为 Y,任取 3 个球，可能有：12A，12B，12C，12Y，1AB，1
4、AC，1AY，1BC，1BY，1CY，2AB，2AC，2AY，2BC，2BY，2CY，ABC，ABY ，ACY，BCY ，共 20 种，3 种颜色的有：1AY，1BY，1CY，2AY ，2BY，2CY，共 6 种只有 1 种颜色的有：ABC，共 1 种，所以，所求概率为：P 2073方法二：从 6 个球中任取 3 个球，共有 20 种，6C恰有两种颜色的概率 1212133663120P方法三：从反面考虑： 1326C8在 中， 为线段 的中点， 为线段 垂直平分ABC 0,4,5,ABD BCEBC线 上任一异于 的点，则 （ ）lDEA B C D7727474答案：A考点：平面向量的三角
5、形法则，平行四边形法则，数量积。解析：由 ，得：ABAC，因为AB4，BC5，0C由勾股定理，得：AC 3，21172AEBDEBACDEBACDCBAE9已知函数 在区间 上单调递增，则 的最大值为（ ）()2sin4fxx0,8A B1 C2 D412答案：C考点：正弦函数的图象及其性质。解析：当 时， ，则由题意可得 ，解得 ，0,8x,484x842 2即 的最大值为 210已知 为抛物线 上两点， 为坐标原点，且 ，则 的最小值为（ ,AB2yOAOB）A B C8 D 42 82答案：C考点：抛物线的性质，两点之间距离公式，基本不等式。解析：设直线 OA 为： ，因为 ，所以，直线
6、 OB 为： ，ykxOAB1yxk，得：A（ ， ） ，同理可得：B（ ， ） ，24ykx2424k所以，AB 22()()kk4216k8，4216162当且仅当 1 时，取等号，所以，AB最小值为 8。k11若 满足约束条件 ，则 的取值范围为（ ）,xy236xy (1)xyA B C D3,09,490,893,8答案：D考点：线性规划。解析：由 ，得 ，作可行域如图所示，236xy 2236xy 其中 ，则 表示以点 和 的连线段1,(,0)1,(,0)22ABCD(1)zxy(,)xy1,0)为对角线的长方形的面积（可为负值） ，当 位于线段 时，(,)y 3:22AD ，因为
7、 ，所以 ；2(1)(23)zxyyy302y 90,8z当 位于线段 时， ；, 6:(1)xCD 2(1)()3,0zxx当 位于线段 时，(,)xy3:20Byy ；21(1)(),8z 当 位于线段 时， (,)xy36:()xAByx 233(1)(),08zxyx综上可知， 的取值范围是 (1)z9,832112348 6 4 2 2 4 6CAB D432112348 6 4 2 2 4 6 8CABD 432112348 6 2 2 4 6 8CABD解法 2：由 ，得 ，作出函数 的图象，使其经过可行域内的点，当()zxy1zxzyx与直线 相切时， 取得最大值，设切点为横坐
8、标为 ，因为1y:2ADt，2()zx所以 ，解得 ，即 ，21()ttz1298tzmax当 过点 时， 取得最小值 1yx3,Cmin3(1)2z综上可知， 的取值范围是 ()zy93,812已知函数 ，若关于 的不等式 恒成立，则实数ln()(0)xfeaax()0fx的取值范围为（ ）aA B C D 2(0,e2(0,)e21,e2(1,)e答案：B考点：函数的导数及其应用。解析：函数 的定义域为 ，由 ，得 ，()fx(1,)()ln()0xfeaa1ln()xea函数 与函数 互为反函数，其图象关于直线 对称，所以要使得1xeyaln()yaxyx恒成立，只需 恒成立，即 恒成立
9、，设 ，则()0fx1xe1xea()1xeg，可知当 时， 取得最小值 ，所以 ，又因为 ，所以 的2)()1xeg2x()gx22a0a取值范围是 0,)二、填空题：本题共 4 小题，每小题 5 分，共 20 分把答案填在题中的横线上13 展开式中 项的系数为 7(2)x7x答案： 1考点：二项式定理。解析：展开式中含 的项为 ，故展开式中 项的系数为 7x16777(2)12Cxx7x1214函数 在点 处的切线方程为 ，则实数 的值为 ln()ya0,ya答案： e考点：函数的导数及其应用。解析： ，当 时， ，解得 l()xyaln1yae15已知正项数列 满足 ，前 项和 满足 ，
10、则数列n1S214(3)(,)nnN的通项公式为 nana答案： 21考点：归纳推理，数学归纳法。解析：当 时， ；当 时，22124(3)6,4,3SSan，2334()6,9,5Saa当 时， ，猜想得 ，经验证，当 时，n2433(),721n21na，满足 故 ，下面用数学归纳法证明：213,nnaS21()nSana ， ，满足 ，2设 时，结论成立，即 ， ，k 2k2k则 2222 21 114(3)()4(),(),(1)1kk kkkSaSaSk ，也满足 ，na结合可知， 2116在棱长为 1 的正方体 中，点 关于平面 的对称点为 ，则 到平1ABCDA1BDCM面的距离
11、为 1ABCD答案： 53考点：几何体的割补，应用立体几何知识求解综合题。解析：将正方体 再叠加一个正方体，构成如图所示的正四棱柱1ABCD，则平面 即为平面 ，连接 ，与平面 ，平面12ABCD121ABCD22ABD交于 两点，2,PQ易证得平面 平面 ，且 平面 ， 平面 ，且 两点是线2/2BCD2222C,PQ段 的两个三等分点，所以点 即为点 关于平面 的对称点为 ，易知点 平面ACA1BDM的距离为 1BD53ACBDA1D1 C1B1B2C2D2A2PQ三、解答题：共 70 分解答应写出文字说明、证明过程或演算步骤第 1721 题为必考题，每个试题考生都必须作答第 22、23
12、题为选考题，考生根据要求作答（一）必考题：共 60 分17 （本小题满分 12 分）在 中，角 的对边分别为 已知 ABC , ,abc2,3sini0bCA（1 ）求 ；c（2 ）求 的面积17解析：（1）由 ，知 ，sin2i0Asinosi0C，而 ，222,()0abcacba 2,3b，2(49)10即 ，而 6 分3,()3(4)0ccc,4c（2 ）在 中，由余弦定理得： ，ABC22 21315os,sin1cos6abBB所以 的面积 12 135in424Sac分解法 2： ，由海伦公式得：9,34,()2abpbc的面积 12ABC 5315() 4Sa分18 （本小题满
13、分 12 分）如图，已知四边形 为梯形， 为矩形，平面 平ABCD1/,90,CDAB1BD面 ，又 1,2（1 ）证明： ；1（2 ）求二面角 的余弦值BADCABCB1DD118解法一：（1 ） 为矩形，且平面 平面 ，1BD1BC平面 平面 ，在 中，B,ACACRtD，1115,2,D在梯形 中， ，从90,1,2,5,2DBBACB而 13BC在 中， ，可知 ， 1115,311D在 中， ，可知 ，1A 2,5ABC1BA又 ，1BD平面 ，又 平面 6 分1C1D11,D（2 ）取 的中点 ，连接 ，由 知 ，AE,BC2AB11EA由 知 ， 为二面角 的平面角15D1A1E
14、1C由（1）知 平面 ， ，又 ，1BC1D1901362， 2132CEB113cosBECABCB1DD1x yzABCB1DD1E解法二：（1） 为矩形，且平面 平面 ， 平面 ，又1D1BDC1ACD，所以可以以 为原点建立如图所示空间直角坐标系，则C，11(,0)(,)(0,2)(,0)(,)(0,)AB11 1, 0,CBABA（2 ） ，(,)(,)(,2)D设平面 的法向量为 ，则 ，令 ，得1AB1,mxyz110mDxzBy 1x(,)m设平面 的法向量为 ，则 ，令 ，1DC2(,)nxyz120nAxzCy21得 (2,)n，3cos,mn因为二面角 为锐角，所以二面角
15、 的余弦值为 1BADC1BADC319 （本小题满分 12 分）一个工厂在某年连续 10 个月每月产品的总成本 y（万元）与该月产量 x（万件）之间有如下一组数据：x 1.08 1.12 1.19 1.28 1.36 1.48 1.59 1.68 1.80 1.87y 2.25 2.37 2.40 2.55 2.64 2.75 2.92 3.03 3.14 3.26（1 ）通过画散点图，发现可用线性回归模型拟合 y 与 x 的关系，请用相关系数加以说明；（2 ） 建立月总成本 y 与月产量 x 之间的回归方程；通过建立的 y 关于 x 的回归方程，估计某月产量为 1.98 万件时，此时产品的
16、总成本为多少万元？（均精确到 0.001）附注：参考数据： ，10104.5,27.3i iy，10102 2.8,.4,1.2i ix b参考公式：相关系数 ，1221nini ixyry回归方程 中斜率和截距的最小二乘估计公式分别为： yabx 12 ,niixybaybx19解析：（1）由已知条件得： ，10210.851.2.974iixrby 这说明 与 正相关，且相关性很yx强5 分（2 ） 由已知求得 ，1.45,2.73,2.731450.96yayx所以所求回归直线方程为 8 分0965x当 时， （万元） ，1.98x8.8y此时产品的总成本为 3.385 万元12 分20
17、 （本小题满分 12 分）已知椭圆 的长轴长为 4，离心率为 2:1(0)xyab2（1 ）求椭圆 的标准方程；（2 ）过 作动直线 交椭圆 于 两点， 为平面上一点，直线 的斜率分(,0)PAB,Q,QABP别为，且满足 ，问 点是否在某定直线上运动，若存在，求出该直线方程；若不120,k120kQ存在，请说明理由20解析：（1）依题意， ，而 ，4,2a22,cebaca从而椭圆的方程为 421xy分（2 ）方法 1：当直线 的斜率存在时，设直线 与椭圆交于 ，AB:(1)ABykx12(,)(,)AxyB设 ，将 代入 ，得 ，显然0(,)Qxy(1)kx240y22()40k，由已知条
18、件 ，得 ，2124kx 120k10201yyxx即 ，将 代入，整理得：0100201yyx12(),()ykyk，而 ，所以 ，1020()()(xkkx0x1200xx即： ， ，012120()xx220 044(1)1kxxk即 20 000484,kk当直线 的斜率不存在时，经检验符合题意AB综上，点 的轨迹方程为： 12Qx分方法 2：当直线 的斜率存在时，设直线 与椭圆交于 ，:(1)ABykx12(,)(,)AxyB设 ，将 代入 ，得 ，显然0(,)xy(1)kx2402240k，21241kx直线 的斜率 ，同理 ，AQ1010001()ykxykxyk0022kxy1
19、01200 00 21020 20() ()()kx kxxxx ，将代入，由 ，得：120k，2000204(1)22() 1xkykxyx 所以 ，0002200()()4kx，0002200(1()1ykxkxy 又 ， ，0()22000()4kxx，2 2201(1kx4当直线 的斜率不存在时，经检验符合题意AB综上，点 的轨迹方程为： 12Q4x分21 （本小题满分 12 分）已知函数 2()(0)xfxae（1 ）若函数 在区间 上单调递减，求实数 的取值范围；,a（2 ）设 的两个极值点为 ，证明：当 时， ()fx121,()x215 12()0fxf（附注： ）ln12.3
20、9821解析：（1）由 ，得2()xfae，22()2)()()xx xfxaeeae， 有两个不同的实根 ，40a122,()x，221 4,axx所以函数 在 上单调递减，在 上单调递增，在 上单调递减()f1,12(,)x2,)x所以要 在 上单调递减，只需 ，即 ，fx2,224a 46a，从而 24(6)0aa 83所以所求 的取值范围是 6 分0,（2 ）解： 是 的极值点 ，212()(),xfxae()fx12()x是关于 的方程 两个实根， ，1,012,aa又 ，122212()()()xxfxfee，211112120()aaax，222 2()xxx，111221()(
21、)ffxee又 12 211212211221()0()()0()()0xx xff xe，令 ，则 ，21tx22211()445txa从而只需 对 恒成立()0te5t令 ，而 在 上单调递增，)2tht ()1()thte2,5，12 12125 517()0,()5tet e又 125ln12.398.4,()0eht12 分（二）选考题：共 10 分请考生在第 22、23 题中任选一题作答如果多做，则按所作的第一题计分22 【 选修 44：坐标系与参数方程】 （本小题满分 10 分）以坐标原点 为极点， 轴正半轴为极轴，建立极坐标系，曲线 ，曲线Ox 21:4sin30C22:sin
22、04C（1 ）求 的直角坐标方程；12,（2 ）已知曲线 与 轴交于 两点， 为 上任一点，求 的最小值y,ABP2CPAB22解析：（1）由 ，得 ，21:4sin30C430xy即 的直角坐标方程为 ；xy由 ，得 ，22:sin0422sincos0,10yx即 的直角坐标方程为 5 分2C1xy（2 ） 与 轴交于点 ，230xy(0,3),1AB而 关于直线 的对称点为 ，(0,1)Bx2102()()5PAPB分 432112348 6 4 2 2 4 6 8BABC1OP23 【 选修 45：不等式选讲】 （本小题满分 10 分）已知函数 ()21,Rfxxa（1 ）当 时，求不等式 的解集；a()0f（2 ）若关于 的不等式 在 时恒成立，求实数 的取值范围xx a23解析：（1）当 时，由 ，得 ， ，1()f21x224(1)()x，解得 或 ，所以 的解集(3)0x3x()0f为 5 分,（2 ） 对 恒成立，即 ，()1fxxa Rx21xax即 ， 对 恒成立，2 21 R显然 ，min0x令 ，则 ， 在 单调递增，()21g4,()21xg ()gx,1，max10 分 0
