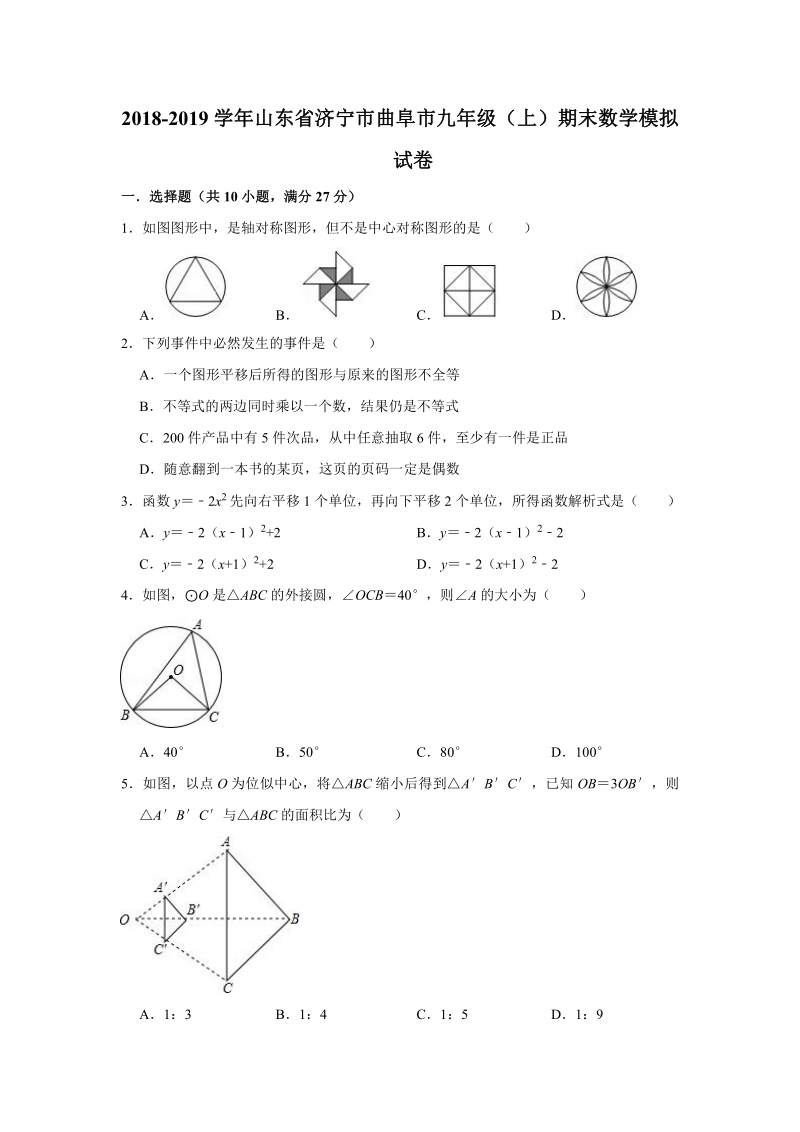
1、2018-2019 学 年 山 东 省 济 宁 市 曲 阜 市 九 年 级 （ 上 ） 期 末 数 学 模 拟试 卷一 选 择 题 （ 共 10 小 题 ， 满 分 27 分 ）1 如 图 图 形 中 ， 是 轴 对 称 图 形 ， 但 不 是 中 心 对 称 图 形 的 是 （ ）A B C D2 下 列 事 件 中 必 然 发 生 的 事 件 是 （ ）A 一 个 图 形 平 移 后 所 得 的 图 形 与 原 来 的 图 形 不 全 等B 不 等 式 的 两 边 同 时 乘 以 一 个 数 ， 结 果 仍 是 不 等 式C 200 件 产 品 中 有 5 件 次 品 ， 从 中 任 意
2、抽 取 6 件 ， 至 少 有 一 件 是 正 品D 随 意 翻 到 一 本 书 的 某 页 ， 这 页 的 页 码 一 定 是 偶 数3 函 数 y 2x2 先 向 右 平 移 1 个 单 位 ， 再 向 下 平 移 2 个 单 位 ， 所 得 函 数 解 析 式 是 （ ）A y 2（ x 1） 2+2 B y 2（ x 1） 2 2C y 2（ x+1） 2+2 D y 2（ x+1） 2 24 如 图 ， O 是 ABC 的 外 接 圆 ， OCB 40 ， 则 A 的 大 小 为 （ ）A 40 B 50 C 80 D 1005 如 图 ， 以 点 O 为 位 似 中 心 ， 将 A
3、BC 缩 小 后 得 到 A B C ， 已 知 OB 3OB ， 则 A B C 与 ABC 的 面 积 比 为 （ ）A 1： 3 B 1： 4 C 1： 5 D 1： 96 下 列 关 于 x 的 方 程 中 一 定 没 有 实 数 根 的 是 （ ）A x2 x 1 0 B 4x2 6x+9 0 C x2 x D x2 mx 2 07 对 于 二 次 函 数 y x2+2x 有 下 列 四 个 结 论 ： 它 的 对 称 轴 是 直 线 x 1； 设 y1 x12+2x1， y2 x22+2x2， 则 当 x2 x1 时 ， 有 y2 y1； 它 的 图 象 与 x 轴 的 两 个 交
4、 点 是 （ 0，0） 和 （ 2， 0） ； 当 0 x 2 时 ， y 0 其 中 正 确 的 结 论 的 个 数 为 （ ）A 1 B 2 C 3 D 48 点 M（ a， 2a） 在 反 比 例 函 数 y 的 图 象 上 ， 那 么 a 的 值 是 （ ）A 4 B 4 C 2 D 29 如 图 ， 正 六 边 形 ABCDEF 内 接 于 O， O 的 半 径 为 4， 则 这 个 正 六 边 形 的 边 心 距 OM和 的 长 分 别 为 （ ）A 2， B ， C 2 ， D 2 ，10 方 程 x2+4x 1 0 的 根 可 视 为 函 数 y x+4 的 图 象 与 函 数
5、 的 图 象 交 点 的 横 坐 标 ， 那么 用 此 方 法 可 推 断 出 ： 当 m 取 任 意 正 实 数 时 ， 方 程 x3+mx 1 0 的 实 根 x0 一 定 在 （ ）范 围 内 A 1 x0 0 B 0 x0 1 C 1 x0 2 D 2 x0 3二 填 空 题 （ 共 5 小 题 ， 满 分 15 分 ， 每 小 题 3 分 ）11 在 平 面 直 角 坐 标 系 中 ， 点 A（ 2， 3） 绕 原 点 O 逆 时 针 旋 转 90 的 对 应 点 的 坐 标 为 12 设 a， b 是 方 程 x2+x 2011 0 的 两 个 实 数 根 ， 则 a2+2a+b
6、的 值 为 13 抛 掷 一 枚 均 匀 的 硬 币 ， 前 5 次 都 正 面 朝 上 ， 则 抛 掷 第 50 次 正 面 朝 上 的 概 率 是 14 如 图 ， 在 O 中 ， CD 是 直 径 ， 弦 AB CD， 垂 足 为 E， 连 接 BC， 若 AB 2 cm， BCD 22 30 ， 则 O 的 半 径 为 cm15 如 图 为 二 次 函 数 y ax2+bx+c（ a 0） 的 图 象 ，下 列 说 法 正 确 的 有 abc 0； a+b+c 0；b2 4ac 0当 x 1 时 ， y 随 x 的 增 大 而 增 大 ；方 程 ax2+bx+c 0（ a 0） 的 根
7、 是 x1 1， x2 3三 解 答 题 （ 共 7 小 题 ， 满 分 55 分 ）16 解 方 程 ： x2 6x+4 0（ 用 配 方 法 ）17 如 图 ， AB 是 O 的 直 径 ， 点 C 是 O 上 一 点 ， 连 接 BC， AC， OD BC 于 E（ 1） 求 证 ： OD AC；（ 2） 若 BC 8， DE 3， 求 O 的 直 径 18 淮 北 市 某 中 学 七 年 级 一 位 同 学 不 幸 得 了 重 病 ， 牵 动 了 全 校 师 生 的 心 ， 该 校 开 展 了 “ 献 爱心 ” 捐 款 活 动 第 一 天 收 到 捐 款 10 000 元 ， 第 三
8、天 收 到 捐 款 12 100 元 （ 1） 如 果 第 二 天 、 第 三 天 收 到 捐 款 的 增 长 率 相 同 ， 求 捐 款 增 长 率 ；（ 2） 按 照 （ 1） 中 收 到 捐 款 的 增 长 速 度 ， 第 四 天 该 校 能 收 到 多 少 捐 款 ？19 如 图 ， 已 知 反 比 例 函 数 y 的 图 象 与 一 次 函 数 y x+b 的 图 象 交 于 点 A（ 1， 4） ， 点 B（ 4， n） （ 1） 求 n 和 b 的 值 ；（ 2） 求 OAB 的 面 积 ；（ 3） 直 接 写 出 一 次 函 数 值 大 于 反 比 例 函 数 值 的 自 变
9、量 x 的 取 值 范 围 20 在 甲 、 乙 两 个 不 透 明 的 布 袋 中 ， 甲 袋 装 有 3 个 完 全 相 同 的 小 球 ， 分 别 标 有 数 字 0， 1， 2；乙 袋 装 有 3 个 完 全 相 同 的 小 球 ， 分 别 标 有 数 字 1， 2， 0； 现 从 甲 袋 中 随 机 抽 取 一 个 小球 ， 小 球 上 的 数 字 记 为 x， 再 从 乙 袋 中 随 机 抽 取 一 个 小 球 ， 小 球 上 的 数 字 记 为 y， 设 点 M的 坐 标 为 （ x， y） （ 1） 用 树 形 图 或 列 表 法 求 出 点 M 的 所 有 等 可 能 个 数
10、 ；（ 2） 分 别 求 点 M 在 函 数 y x+1 图 象 上 的 概 率 和 点 M 在 第 四 象 限 的 概 率 21 我 们 定 义 ： 如 图 1， 在 ABC 看 ， 把 AB 点 A 顺 时 针 旋 转 （ 0 180 ） 得 到 AB，把 AC 绕 点 A 逆 时 针 旋 转 得 到 AC， 连 接 BC 当 + 180 时 ， 我 们 称 ABC是 ABC 的 “ 旋 补 三 角 形 ” ， ABC边 BC上 的 中 线 AD 叫 做 ABC 的 “ 旋 补 中 线 ” ， 点 A 叫做 “ 旋 补 中 心 ” 特 例 感 知 ：（ 1） 在 图 2， 图 3 中 ，
11、ABC是 ABC 的 “ 旋 补 三 角 形 ” ， AD 是 ABC 的 “ 旋 补 中 线 ” 如 图 2， 当 ABC 为 等 边 三 角 形 时 ， AD 与 BC 的 数 量 关 系 为 AD BC；如 图 3， 当 BAC 90 ， BC 8 时 ， 则 AD 长 为 猜 想 论 证 ：（ 2） 在 图 1 中 ， 当 ABC 为 任 意 三 角 形 时 ， 猜 想 AD 与 BC 的 数 量 关 系 ， 并 给 予 证明 22 如 图 ， 点 A， B， C 都 在 抛 物 线 y ax2 2amx+am2+2m 5（ a 0） 上 ， AB x 轴 ， ABC 135 ， 且
12、AB 4（ 1） 填 空 ： 抛 物 线 的 顶 点 坐 标 为 ； （ 用 含 m 的 代 数 式 表 示 ） ；（ 2） 求 ABC 的 面 积 （ 用 含 a 的 代 数 式 表 示 ） ；（ 3） 若 ABC 的 面 积 为 2， 当 2m 5 x 2m 2 时 ， y 的 最 大 值 为 2， 求 m 的 值 参 考 答 案一 选 择 题 （ 共 10 小 题 ， 满 分 27 分 ）1 【 解 答 】 解 ： A、 是 轴 对 称 图 形 ， 不 是 中 心 对 称 图 形 ， 故 此 选 项 正 确 ；B、 不 是 轴 对 称 图 形 ， 是 中 心 对 称 图 形 ， 故 此
13、选 项 错 误 ；C、 是 轴 对 称 图 形 ， 也 是 中 心 对 称 图 形 ， 故 此 选 项 错 误 ；D、 是 轴 对 称 图 形 ， 也 是 中 心 对 称 图 形 ， 故 此 选 项 错 误 故 选 ： A2 【 解 答 】 解 ： A、 一 个 图 形 平 移 后 所 得 的 图 形 与 原 来 的 图 形 不 全 等 ， 是 不 可 能 事 件 ， 故 此选 项 错 误 ；B、 不 等 式 的 两 边 同 时 乘 以 一 个 数 ， 结 果 仍 是 不 等 式 ， 是 随 机 事 件 ， 故 此 选 项 错 误 ；C、 200 件 产 品 中 有 5 件 次 品 ， 从 中
14、 任 意 抽 取 6 件 ， 至 少 有 一 件 是 正 品 ， 是 必 然 事 件 ， 故 此选 项 正 确 ；D、 随 意 翻 到 一 本 书 的 某 页 ， 这 页 的 页 码 一 定 是 偶 数 ， 是 随 机 事 件 ， 故 此 选 项 错 误 ；故 选 ： C3 【 解 答 】 解 ： 抛 物 线 y 2x2 的 顶 点 坐 标 为 （ 0， 0） ， 把 （ 0， 0） 先 向 右 平 移 1 个 单 位 ，再 向 下 平 移 2 个 单 位 所 得 对 应 点 的 坐 标 为 （ 1， 2） ， 所 以 平 移 后 的 抛 物 线 解 析 式 为 y 2（ x 1）2 2故 选
15、 ： B4 【 解 答 】 解 ： OB OC BOC 180 2 OCB 100 ， 由 圆 周 角 定 理 可 知 ： A BOC 50故 选 ： B5 【 解 答 】 解 ： OB 3OB ， ， 以 点 O 为 位 似 中 心 ， 将 ABC 缩 小 后 得 到 A B C ， A B C ABC， ，故 选 ： D6 【 解 答 】 解 ： A、 5 0， 方 程 有 两 个 不 相 等 的 实 数 根 ；B、 108 0， 方 程 没 有 实 数 根 ；C、 1 0， 方 程 有 两 个 相 等 的 实 数 根 ；D、 m2+8 0， 方 程 有 两 个 不 相 等 的 实 数 根
16、 故 选 ： B7 【 解 答 】 解 ： y x2+2x （ x 1） 2+1， 故 它 的 对 称 轴 是 直 线 x 1， 正 确 ； 直 线 x 1 两 旁 部 分 增 减 性 不 一 样 ， 设 y1 x12+2x1， y2 x22+2x2， 则 当 x2 x1 时 ，有 y2 y1 或 y2 y1 或 y2 y1， 错 误 ；当 y 0， 则 x（ x+2） 0， 解 得 ： x1 0， x2 2，故 它 的 图 象 与 x 轴 的 两 个 交 点 是 （ 0， 0） 和 （ 2， 0） ， 正 确 ； a 1 0， 抛 物 线 开 口 向 下 ， 它 的 图 象 与 x 轴 的
17、两 个 交 点 是 （ 0， 0） 和 （ 2， 0） ， 当 0 x 2 时 ， y 0， 正 确 故 选 ： C8 【 解 答 】 解 ： 点 M（ a， 2a） 在 反 比 例 函 数 y 的 图 象 上 2a 解 得 ： a 2，故 选 ： D9 【 解 答 】 解 ： 如 图 所 示 ， 连 接 OC、 OB， 多 边 形 ABCDEF 是 正 六 边 形 ， BOC 60 ， OA OB， BOC 是 等 边 三 角 形 ， OBM 60 ， OM OBsin OBM 4 2 ，的 长 ；故 选 ： D10 【 解 答 】 解 ： 方 程 x3+mx 1 0 变 形 为 x2+m
18、0， 方 程 x3+mx 1 0 的 根 可 视 为 函 数 y x2+m 的 图 象 与 函 数 的 图 象 交 点 的 横 坐 标 ， 当 m 取 任 意 正 实 数 时 ， 函 数 y x2+m 的 图 象 过 第 一 、 二 象 限 ， 函 数 的 图 象 分 别 在 第一 、 三 象 限 ， 它 们 的 交 点 在 第 一 象 限 ， 即 它 们 的 交 点 的 横 坐 标 为 正 数 ， 当 m 取 任 意 正 实 数 时 ， 函 数 y x2+m 的 图 象 沿 y 轴 上 下 平 移 ， 且 总 在 x 轴 上 方 ， 抛 物 线顶 点 越 低 ， 与 函 数 的 图 象 的
19、交 点 的 横 坐 标 越 大 ，当 m 0 时 ， y x2 与 的 交 点 A 的 坐 标 为 （ 1， 1） ， 当 m 取 任 意 正 实 数 时 ， 方 程 x3+mx 1 0 的 实 根 x0 一 定 在 0 x0 1 的 范 围 内 故 选 ： B二 填 空 题 （ 共 5 小 题 ， 满 分 15 分 ， 每 小 题 3 分 ）11 【 解 答 】 解 ： 如 图 ， 线 段 OA 绕 原 点 O 逆 时 针 旋 转 90 得 到 OA ， 则 点 A 的 坐 标 为（ 3， 2） ， 点 A 在 第 二 象 限 故 答 案 为 （ 3， 2） 12 【 解 答 】 解 ： a
20、 是 方 程 x2+x 2011 0 的 实 数 根 ， a2+a 2011 0， 即 a2 a+2011， a2+2a+b a+2011+2a+b a+b+2011， a， b 是 方 程 x2+x 2011 0 的 两 个 实 数 根 ， a+b 1， a2+2a+b 1+2011 2010故 答 案 为 201013 【 解 答 】 解 ： 硬 币 由 正 面 朝 上 和 朝 下 两 种 情 况 ， 并 且 是 等 可 能 ， 第 50 次 正 面 朝 上 的 概 率 是 ，故 答 案 为 ： 14 【 解 答 】 解 ： 连 结 OB， 如 图 ， BCD 22 30 ， BOD 2
21、BCD 45 ， AB CD， BE AE AB 2 ， BOE 为 等 腰 直 角 三 角 形 ， OB BE 2（ cm） 故 答 案 为 ： 215 【 解 答 】 解 ： 抛 物 线 开 口 向 上 ， 对 称 轴 在 y 轴 右 侧 ， 与 y 轴 交 于 负 半 轴 ， a 0， 0， c 0， b 0， abc 0， 结 论 正 确 ； 当 x 1 时 ， y 0， a+b+c 0， 结 论 错 误 ； 抛 物 线 与 x 轴 有 两 个 交 点 ， b2 4ac 0， 结 论 错 误 ； 抛 物 线 与 x 轴 交 于 点 （ 1， 0） ， （ 3， 0） ， 抛 物 线 的
22、 对 称 轴 为 直 线 x 1 抛 物 线 开 口 向 上 ， 当 x 1 时 ， y 随 x 的 增 大 而 增 大 ， 结 论 正 确 ； 抛 物 线 与 x 轴 交 于 点 （ 1， 0） ， （ 3， 0） ， 方 程 ax2+bx+c 0（ a 0） 的 根 是 x1 1， x2 3， 结 论 正 确 故 答 案 为 ： 三 解 答 题 （ 共 7 小 题 ， 满 分 55 分 ）16 【 解 答 】 解 ： 由 原 方 程 移 项 ， 得x2 6x 4，等 式 的 两 边 同 时 加 上 一 次 项 系 数 的 一 半 的 平 方 ， 得x2 6x+9 4+9，即 （ x 3）2
23、 5， x +3， x1 +3， x2 +317 【 解 答 】 （ 1） 证 明 ： AB 是 O 的 直 径 ， C 90 ， OD BC， OEB C 90 ， OD AC；（ 2） 解 ： 令 O 的 半 径 为 r，根 据 垂 径 定 理 可 得 ： BE CE BC 4，由 勾 股 定 理 得 ： r2 42+（ r 3） 2，解 得 ： r ，所 以 O 的 直 径 为 18 【 解 答 】 解 ： （ 1） 捐 款 增 长 率 为 x， 根 据 题 意 得 ：10000（ 1+x） 2 12100，解 得 ： x1 0.1， x2 2.1（ 舍 去 ） 则 x 0.1 10%答
24、 ： 捐 款 的 增 长 率 为 10%（ 2） 根 据 题 意 得 ： 12100 （ 1+10%） 13310（ 元 ） ，答 ： 第 四 天 该 校 能 收 到 的 捐 款 是 13310 元 19 【 解 答 】 解 ： （ 1） 把 A 点 （ 1， 4） 分 别 代 入 反 比 例 函 数 y ， 一 次 函 数 y x+b，得 k 1 4， 1+b 4，解 得 k 4， b 3， 点 B（ 4， n） 也 在 反 比 例 函 数 y 的 图 象 上 ， n 1；（ 2） 如 图 ， 设 直 线 y x+3 与 y 轴 的 交 点 为 C， 当 x 0 时 ， y 3， C（ 0，
25、 3） ， S AOB S AOC+S BOC 3 1+ 3 4 7.5；（ 3） B（ 4， 1） ， A（ 1， 4） ， 根 据 图 象 可 知 ： 当 x 1 或 4 x 0 时 ， 一 次 函 数 值 大 于 反 比 例 函 数 值 20 【 解 答 】 解 ： （ 1） 列 表 如 下 ：0 1 2 1 （ 0， 1） （ 1， 1） （ 2， 1） 2 （ 0， 2） （ 1， 2） （ 2， 2）0 （ 0， 0） （ 1， 0） （ 2， 0）所 以 点 M 的 所 有 等 可 能 的 个 数 是 9；（ 2） 满 足 点 （ x， y） 落 在 函 数 y x+1 图 象
26、上 的 结 果 有 2 个 ， 即 （ 2， 1） ， （ 1， 0） ，所 以 点 M（ x， y） 在 函 数 y x+1 图 象 上 的 概 率 是 ，因 为 点 （ 1， 1） ， （ 2， 1） ， （ 1， 2） 和 （ 2， 2） 落 在 第 四 象 限 ，所 以 点 M 在 第 四 象 限 的 概 率 是 21【 解 答 】 解 ：（ 1） 如 图 2， 当 ABC 为 等 边 三 角 形 时 ， AD 与 BC 的 数 量 关 系 为 AD BC；理 由 ： ABC 是 等 边 三 角 形 ， AB BC AC AB AC ， DB DC ， AD B C ， BAC 60
27、， BAC+ B AC 180 ， B AC 120 ， B C 30 ， AD AB BC，故 答 案 为 如 图 3， 当 BAC 90 ， BC 8 时 ， 则 AD 长 为 4理 由 ： BAC 90 ， BAC+ B AC 180 ， B AC BAC 90 ， AB AB ， AC AC ， BAC B AC ， BC B C ， B D DC ， AD B C BC 4，故 答 案 为 4（ 2） 猜 想 证 明 ： 如 图 ， 延 长 AD 至 点 Q， 则 DQB DAC， QB AC， QB AC， QBA+ BAC 180 ， BAC+ BAC 180 ， QBA BAC
28、，又 由 题 意 得 到 QB AC AC， AB AB， AQB BCA， AQ BC 2AD，即 22 【 解 答 】 解 ： （ 1） y ax2 2amx+am2+2m 5 a（ x m） 2+2m 5， 抛 物 线 的 顶 点 坐 标 为 （ m， 2m 5） 故 答 案 为 ： （ m， 2m 5） （ 2） 过 点 C 作 直 线 AB 的 垂 线 ， 交 线 段 AB 的 延 长 线 于 点 D， 如 图 所 示 AB x 轴 ， 且 AB 4， 点 B 的 坐 标 为 （ m+2， 4a+2m 5） ABC 135 ， 设 BD t， 则 CD t， 点 C 的 坐 标 为
29、（ m+2+t， 4a+2m 5 t） 点 C 在 抛 物 线 y a（ x m） 2+2m 5 上 ， 4a+2m 5 t a（ 2+t）2+2m 5，整 理 ， 得 ： at2+（ 4a+1） t 0，解 得 ： t1 0（ 舍 去 ） ， t2 ， S ABC ABCD （ 3） ABC 的 面 积 为 2， 2，解 得 ： a ， 抛 物 线 的 解 析 式 为 y （ x m） 2+2m 5分 三 种 情 况 考 虑 ：当 m 2m 2， 即 m 2 时 ， 有 （ 2m 2 m） 2+2m 5 2，整 理 ， 得 ： m2 14m+39 0，解 得 ： m1 7 （ 舍 去 ） ， m2 7+ （ 舍 去 ） ；当 2m 5 m 2m 2， 即 2 m 5 时 ， 有 2m 5 2，解 得 ： m ；当 m 2m 5， 即 m 5 时 ， 有 （ 2m 5 m） 2+2m 5 2，整 理 ， 得 ： m2 20m+60 0，解 得 ： m3 10 2 （ 舍 去 ） ， m4 10+2 综 上 所 述 ： m 的 值 为 或 10+2
