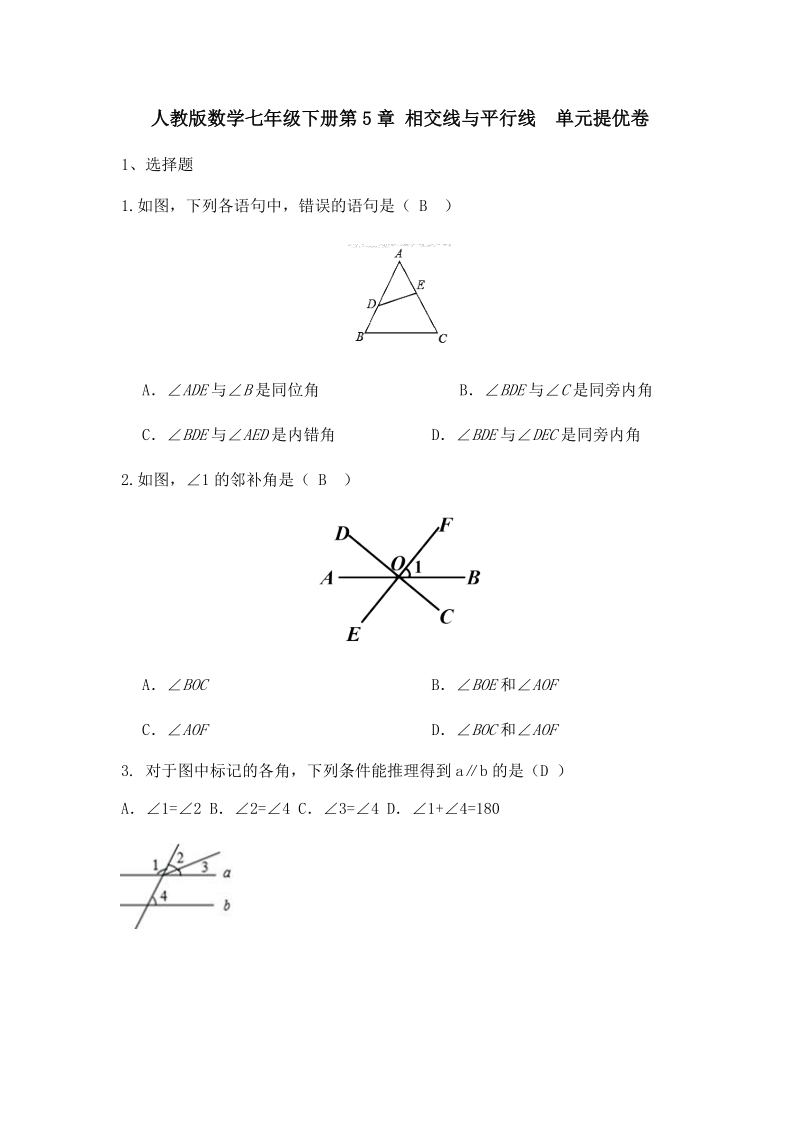
1、人教版数学七年级下册第 5章 相交线与平行线 单元提优卷1、选择题1.如图，下列各语句中，错误的语句是（ B ）A ADE与 B是同位角 B BDE与 C是同旁内角C BDE与 AED是内错角 D BDE与 DEC是同旁内角2.如图，1 的邻补角是（ B ）A BOC B BOE和 AOFC AOF D BOC和 AOF3. 对于图中标记的各角，下列条件能推理得到 ab 的是（D ） A1=2 B2=4 C3=4 D1+4=180 4如图，已知12，则下列结论一定成立的是（B ） AAB/CD BAD/BC CBD D34 5.如图所示，下列说法不正确的是(A)A. 与 是同位角 ABD EC
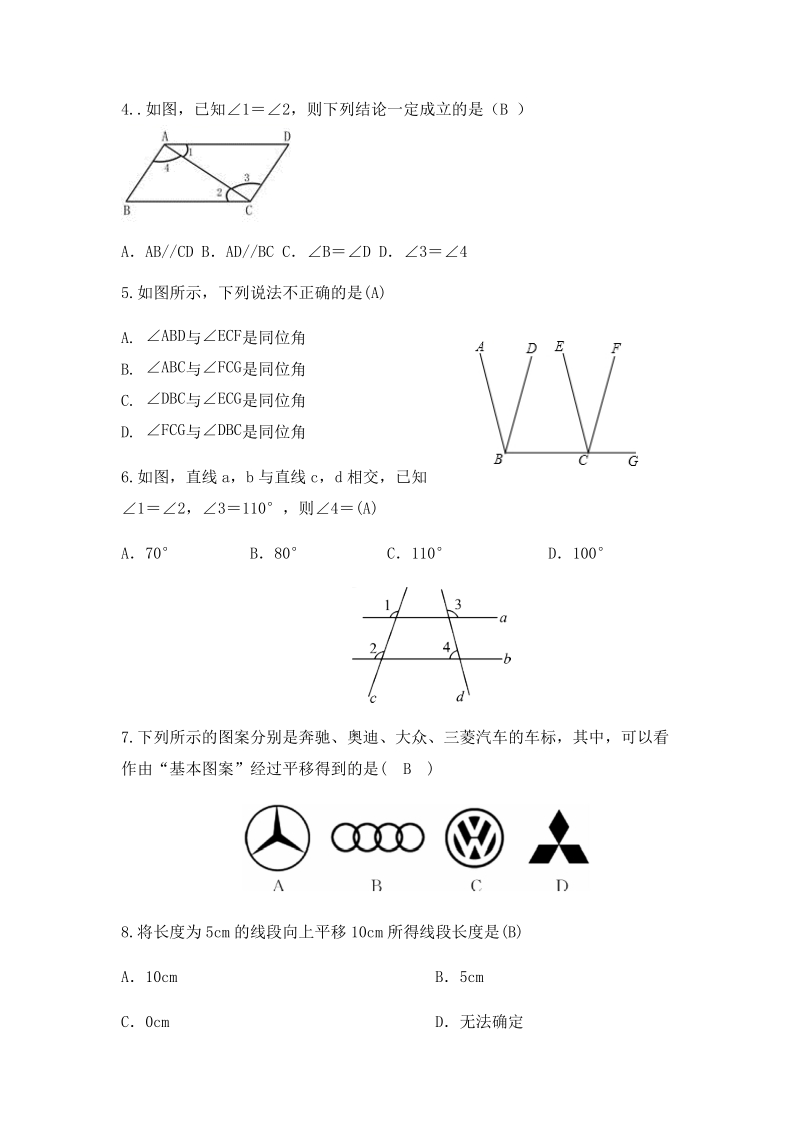
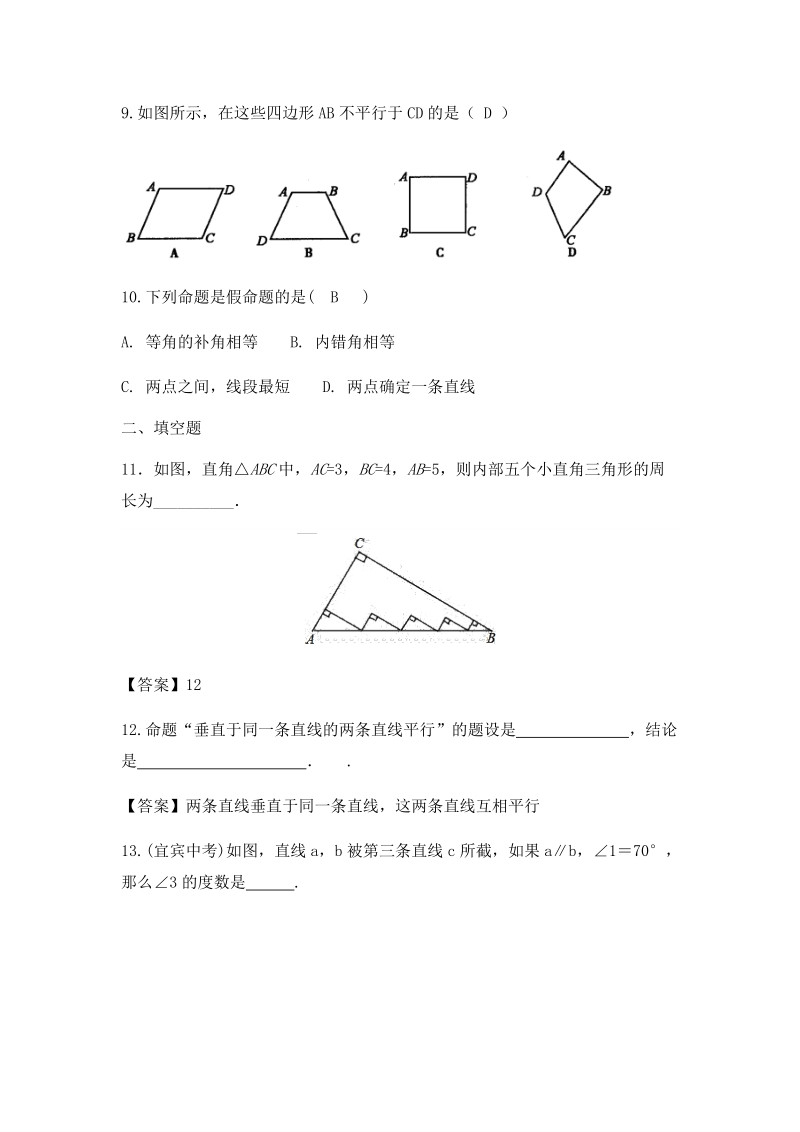
2、FB. 与 是同位角 ABC FCGC. 与 是同位角 DBC ECGD. 与 是同位角 FCG DBC6.如图，直线 a，b 与直线 c，d 相交，已知12，3110，则4(A)A70 B80 C110 D1007.下列所示的图案分别是奔驰、奥迪、大众、三菱汽车的车标，其中，可以看作由“基本图案”经过平移得到的是( B )8.将长度为 5cm的线段向上平移 10cm所得线段长度是(B)A10cm B5cmC0cm D无法确定9.如图所示，在这些四边形 AB不平行于 CD的是（ D ）10.下列命题是假命题的是( B )A. 等角的补角相等 B. 内错角相等C. 两点之间，线段最短 D. 两点
3、确定一条直线二、填空题11如图，直角 ABC中， AC=3， BC=4， AB=5，则内部五个小直角三角形的周长为_【答案】1212.命题“垂直于同一条直线的两条直线平行”的题设是 ，结论是 .【答案】两条直线垂直于同一条直线，这两条直线互相平行13.(宜宾中考)如图，直线 a，b 被第三条直线 c所截，如果 ab，170，那么3 的度数是 .【答案】7014. 已知四边形 ABCD的面积为 ，将该四边形向右平移一定距离后得到新20cm2的四边形 EFGH，则四边形 EFGH的面积为 答案： 20cm215.如图，BCAC，CB8 cm，AC6 cm，点 C到 AB的距离是 4.8 cm，那么
4、点B到 AC的距离是_ cm，点 A到 BC的距离是_ cm， A， B两点间的距离是_ cm.【答案】8 6 10三、解答题16.阅读下列问题后做出相应的解答“同位角相等，两直线平行”和“两直线平行，同位角相等”这两个命题的题设和结论在命题中的位置恰好对调，我们把其中一个命题叫做另一个命题的逆命题请你写出命题“角平分线上的点到角两边的距离相等”的逆命题，并指出逆命题的题设和结论解：逆命题：在角的内部到角两边距离相等的点在这个角的平分线上题设：在角的内部到角两边距离相等的点；结论：点在这个角的平分线上17.阅读下列解答过程：如图甲，ABCD，探索P 与A，C 之间的关系解：过点 P作 PEAB
5、.ABCD，PEABCD(平行于同一条直线的两条直线互相平行)1A180(两直线平行，同旁内角互补)，2C180(两直线平行，同旁内角互补)1A2C360.又APC12，APCAC360.如图乙和图丙，ABCD，请根据上述方法分别探索两图中P 与A，C之间的关系解：如图乙，过点 P作 PEAB.ABCD(已知)，PEABCD(平行于同一直线的两条直线平行)AEPA，EPCC(两直线平行，内错角相等)APCEPAEPC，APCAC(等量代换)如图丙，过点 P作 PFAB.FPAA(两直线平行，内错角相等)ABCD(已知)，PFCD(平行于同一直线的两条直线平行)FPCC(两直线平行，内错角相等)
6、FPCFPAAPC，CAAPC(等量代换)18. 如图，ABEF 于点 B，CDEF 于点 D，12.(1)请说明 ABCD；(2)试判断 BM与 DN是否平行，为什么？解：(1)ABEF，CDEF， ABCD(在同一平面内，垂直于同一条直线的两条直线互相平行)(2)BMDN.理由如下：ABEF，CDEF， ABECDE90(垂直的定义)12， ABE1CDE2， 即MBENDE.BMDN(同位角相等，两直线平行)19.如图 所示，已知， ， ，试回答下列问题： BC/OA B= A=100试说明： ；(1) OB/AC如图 ，若点 E、 F在 BC上，且 ， OE平分 试求(2) FOC=
7、AOC BOF.的度数； EOC在 的条件下，若左右平行移动 AC，如图 ，那么 ： 的比值是(3)(2) OCB OFB否随之发生变化？若变化，试说明理由；若不变，求出这个比值；在 的条件下，当 时，试求 的度数(4)(3) OEB= OCA OCA解： ，(1) BC/OA，又 ， B+ O=180 B= A， A+ O=180； OB/AC， ，(2) B+ BOA=180 B=100， BOA=80平分 ， OE BOF，又 ， BOE= EOF FOC= AOC； EOF+ FOC=12( BOF+ FOA)=12 BOA=40结论： ： 的值不发生变化 理由为：(3) OCB OFB .， BC/OA， FCO= COA又 ， FOC= AOC， FOC= FCO， OFB= FOC+ FCO=2 OCB： ：2； OCB OFB=1由 知： ，(4)(1) OB/AC则 ， OCA= BOC由 可以设： ， ，(2) BOE= EOF= FOC= COA=则 ， OCA= BOC=2 +， OEB= EOC+ ECO= + + = +2， OEB= OCA， 2 + = +2， =， AOB=80， = =20 OCA=2 + =40 +20 =60
