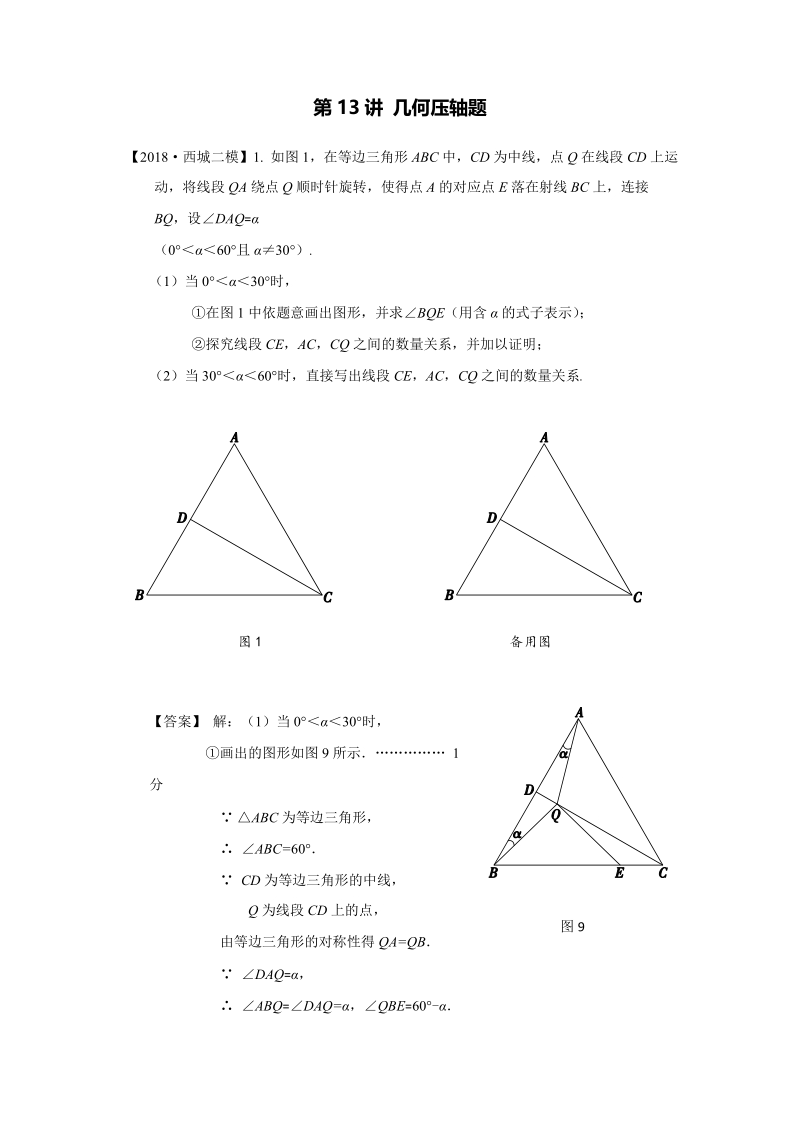
1、第 13 讲 几何压轴题【2018西城二模】1. 如图 1，在等边三角形 ABC 中，CD 为中线，点 Q 在线段 CD 上运动，将线段 QA 绕点 Q 顺时针旋转，使得点 A 的对应点 E 落在射线 BC 上，连接BQ，设DAQ =（0 60且 30 ）.（1）当 030时，在图 1 中依题意画出图形，并求BQE（用含 的式子表示） ；探究线段 CE，AC，CQ 之间的数量关系，并加以证明；（2）当 30 60时，直接写出线段 CE，AC ，CQ 之间的数量关系 . 【答案】 解：（1）当 0 30 时，画出的图形如图 9 所示 1分 ABC 为等边三角形， ABC=60 CD 为等边三角形
2、的中线，Q 为线段 CD 上的点，由等边三角形的对称性得 QA=QB DAQ =， ABQ=DAQ=，QBE= 60-图 1 备用图图 9 线段 QE 为线段 QA 绕点 Q 顺时针旋转所得， QE = QA QB=QE可得 2 分1802(6)0 3 分证法一：如图 10，延长 CA 到点 F，使得 AF=CE，连接 QF，作 QHAC于点 H BQE=60+2 ，点 E 在 BC 上， QEC=BQE+QBE =(60+2)+( 60-)=120+ 点 F 在 CA 的延长线上，DAQ =， QAF=BAF+ DAQ=120+ QAF= QEC 又 AF =CE，QA=QE， QAFQEC
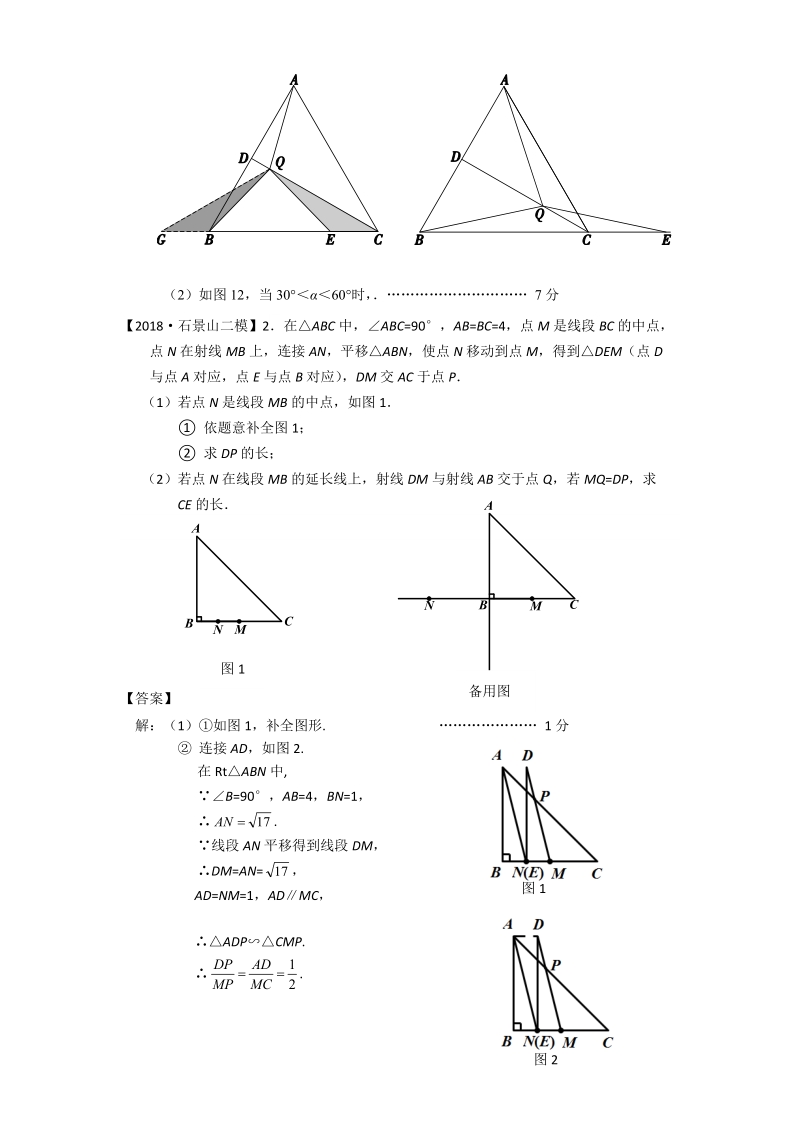
3、 QF=QC QHAC 于点 H， FH=CH，CF=2CH 在等边三角形 ABC 中，CD 为中线，点 Q 在 CD 上， ACQ= =30，12ACB即QCF 为底角为 30的等腰三角形 3coscos02HQC CEAFCH即 6 分思路二：如图 11，延长 CB 到点 G，使得 BG=CE，连接 QG，可得QBG QEC ，QCG 为底角为 30的等腰三角形，与证法一同理可得 CEABC3Q图 10 图 11 图 12（2）如图 12，当 3060时， 7 分【2018 石景山二模】2在 ABC 中，ABC=90，AB=BC=4，点 M 是线段 BC 的中点，点 N 在射线 MB 上，
4、连接 AN，平移ABN，使点 N 移动到点 M，得到DEM（点 D与点 A 对应，点 E 与点 B 对应） ，DM 交 AC 于点 P（1 ）若点 N 是线段 MB 的中点，如图 1 依题意补全图 1； 求 DP 的长；（2 ）若点 N 在线段 MB 的延长线上，射线 DM 与射线 AB 交于点 Q，若 MQ=DP，求CE 的长【答案】解：（1）如图 1，补全图形. 1 分 连接 AD，如图 2.在 Rt ABN 中,B=90，AB=4 ，BN=1， .17AN线段 AN 平移得到线段 DM，DM=AN = ，AD=NM=1，ADMC，ADPCMP. .21MCADP图 1NMABCNMABC
5、备用图图 1图 2 . 3 分317DP（2 ）连接 ，如图 3.NQ由平移知： ，且 = .AMND ， .P ，且 = .P四边形 是平行四边形.ANQ . .45BC又 ，90 . ，ANMQ .B又 是 的中点，且 ，C4ABC .42N (舍负).B .ME . 7 分C（2 ）法二，连接 AD，如图 4.设 CE 长为 x，线段 AB 移动到得到线段 DE， ，ADBM.4BEADADPCMP. .2xMCPMQ=DP， .xDQ104QBMQAD， .xAB42解得 .x . 7 分2CE图 3PNQDEMACBPNQDEMACB图 4【2018海淀二模】3如图，在等边 中， 分
6、别是边 上的点，且ABC ,DE,ACB, ，点 与点 关于 对称，连接CDE30BF， 交 于 .AFG（1）连接 ，则 之间的数量关系是 ,DE；（2）若 ，求 的大小; （用 的式子表BCF示）（2）用等式表示线段 和 之间的数量关系，并证明.,GA【答案】（1） ； DEF（2）解：连接 ， ， 是等边三角形， ABC .60 ， .12D点 与点 关于 对称，CFB ， .0DFC .12由（1）知 .E ， ， 在以 为圆心， 为半径的圆上.FC . 602D（3） .理由如下： BGA连接 ，延长 ， 交于点 ，FH 是等边三角形， C ， .60BCA点 与点 关于 对称，D
7、， .BFGFEDCBAGFEDCBA .BFA .设 ，CD则 .602 .BAF . . C由（2）知 .60E .BGFDB ， .1四边形 中，A.360120EAGF .HF 是等边三角形. G ， .60 ，CDE .AB在 与 中， H ,.GEADB . .H ，FGA B【2018 丰台二模】4如图，正方形 ABCD 中，点 E 是 BC 边上的一个动点，连接AE，将线段 AE 绕点 A 逆时针旋转 90，得到 AF，连接 EF，交对角线 BD 于点G，连接 AG（1）根据题意补全图形；（2）判定 AG 与 EF 的位置关系并证明；（3）当 AB = 3，BE = 2 时，求
8、线段 BG 的长HGFEDCBA54321HMGFABDCEA BCED【答案】解：（1）图形补全后如图 1 分GFABDCE（2 ）结论：AG EF 2 分证明：连接 FD，过 F 点 FMBC ，交 BD 的延长线于点 M四边形 ABCD 是正方形，AB=DA=DC=BC，DAB= ABE= ADC =90，ADB= 5=45 线段 AE 绕点 A 逆时针旋转 90，得到 AF，AE=AF，FAE=901= 2FDAEBA 3 分FDA=EBA=90，FD=BEADC=90，FDA+ADC=180。点 F、 D、C 三点共线ADB=3=45 FM BC，4= 5=45，FM=FD，FM=B
9、E FGM =EGB，FM=BE，4=5，FMG EGB FG=EGAE=AF，AG FE 4 分（3 ） 解：如图，DB 与 FE 交于点 GAB =3，BE =2，DC=3 ，CE=1，FD =2RtDAB 中，DB =3 2四边形 ABCD 是正方形，DH BC ， ，即 ，DHFCE15DH = .25 ，即 ，GBE235BGBG= . 7 分52【2018 房山二模】5. 已知 AC=DC，AC DC，直线 MN 经过点 A，作 DBMN，垂足为 B，连接 CB.（1）直接写出D 与 MAC 之间的数量关系;（2 ） 如图 1，猜想 AB，BD 与 BC 之间的数量关系，并说明理由
10、； 如图 2，直接写出 AB，BD 与 BC 之间的数量关系；（3 ）在 MN 绕点 A 旋转的过程中，当BCD=30，BD= 时，直接写出 BC 的值.2图 2CADBMN图 1CADBM N图 2CADBN【答案】27. 解：（1）相等或互补；2 分（注：每个 1 分）（2 ） 猜想：BD+ AB= 32BC分如图 1，在射线 AM 上截取 AE=BD，连接 CE.又D=EAC ，CD=ACBCDECA BC=EC,BCD=ECAACCDACD=90即ACB+BCD=90 ACB+ECA =90即ECB=90BE= 2BCAE+AB =BE= 2BCBD+AB= 4 分2BC AB BD=
11、 5 分2BC（3）BC= 或 7 分3+1 3 1【2018 东城二模】6. 如图所示，点 P 位于等边 的内部，且ACP =CBP ABC(1) BPC 的度数为_；(2) 延长 BP 至点 D，使得 PD=PC，连接 AD，CDNM图1ECADB依题意，补全图形；证明：AD+CD= BD；(3) 在(2)的条件下，若 BD 的长为 2，求四边形 ABCD 的面积【答案】解：(1)120. -2 分(2)如图 1 所示.在等边 中， ，ABC 60 .P =， 60. 18120.BCBPC .PD =， 为等边三角形. 60ACACPB， .DB在 和 中， ACPD， ， . SB .
12、A -4 分 .CPD（3）如图 2，作 于点 ， 延长线于点 .MA BNC N =60DB， .A C 3=.2BMND又由（2）得， =2ACB，BDCSS 四 边 形 +1AMCDBNA32CD-7 分 32.【2018 朝阳二模】7.如图，在ABC 中，AB=AC，BAC=90，M 是 BC 的中点，延长AM 到点 D，AE= AD，EAD=90，CE 交 AB 于点 F，CD=DF.（1）CAD= 度； （2）求CDF 的度数；（3）用等式表示线段 和 之间的数量关系，并证明.CE【答案】解：（1）45 1 分（2 ）解：如图，连接 DB. ， 是 的中点，90 ABC， MBCB
13、AD= CAD=45.BADCAD . 2 分DBA=DCA，BD = CD.CD=DF,BD =DF. 3 分DBA=DFB= DCA.DFB +DFA =180,DCA+DFA =180.BAC +CDF =180.CDF =90. 4 分（3 ） CE= CD. 5 分21证明： ，90 EADEAF=DAF=45.AD=AE，EAFDAF. 6 分DF=EF.由可知，CF= . 7 分2CDCE = CD.1【2018 昌平二模】8.如图，在 ABC 中，AB= ACBC，BD 是 AC 边上的高，点 C 关于直线BD 的对称点为点 E，连接 BE.（1 ） 依题意补全图形；若BAC
14、= ，求DBE 的大小（用含 的式子表示） ；（2 ） 若 DE=2AE，点 F 是 BE 中点，连接 AF，BD=4，求 AF 的长.（备用图）DCB A DCB A【答案】如图，在ABC 中，AB=AC BC，BD 是 AC 边上的高，点 C 关于直线 BD 的对称点为点 E，连接 BE.（1）补全图形；若BAC= ，求DBE 的大小（用含 的式子表示） ；（2）若 DE=2AE，点 F 是 BE 中点，连接 AF，BD=4，求 AF 的长.（1）解：如图 1 分 AB=AC，BAC= ， ABC= ACB=90- 12点 C 关于直线 BD 的对称点为点 E，BD 是 AC 边上的高. BDCE，CD=DE BE= BC BEC= ACB=90- 2 分12DBE= 3 分（2）解：作 FGAC 于 G，BDCE，FGBD点 F 是 BE 中点， EG=DG 4 分1FBD2DE=2AE ，AE=EG= DG 5 分设 AE=EG=DG=x，则 CD=DE=2x，AC=5x ，AB=AC=5x BD=4x BD=4 ，x =1 6 分AG=2 =2，1FG=BD2AF= 7 分DCB AEEABCDF G
