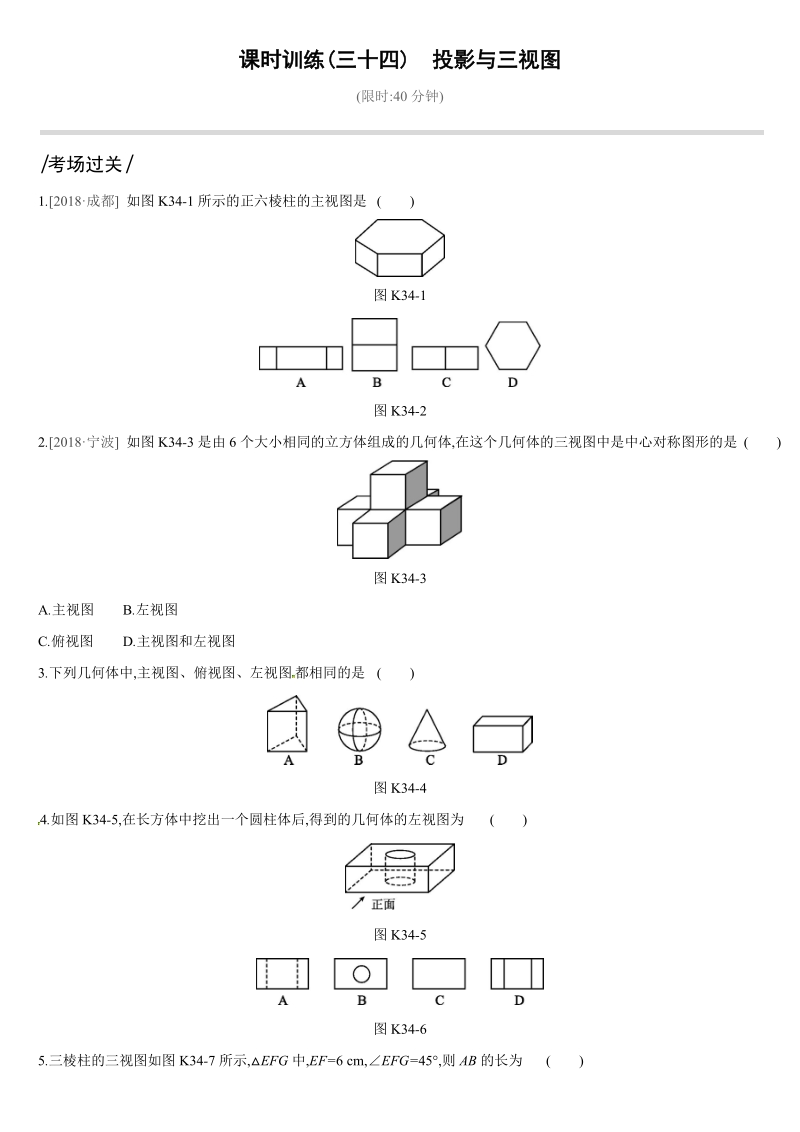
1、课时训练(三十四) 投影与三视图(限时:40 分钟)|考场过关 |1.2018成都 如图 K34-1 所示的正六棱柱的主视图是 ( )图 K34-1图 K34-22.2018宁波 如图 K34-3 是由 6 个大小相同的立方体组成的几何体,在这个几何体的三视图中是中心对称图形的是 ( )图 K34-3A.主视图 B.左视图C.俯视图 D.主视图和左视图3.下列几何体中,主视图、俯视图、左视图 都相同的是 ( )图 K34-44.如图 K34-5,在长方体中挖出一个圆柱体后,得到的几何体的左视图为 ( )图 K34-5图 K34-65.三棱柱的三视图如图 K34-7 所示, EFG 中,EF=
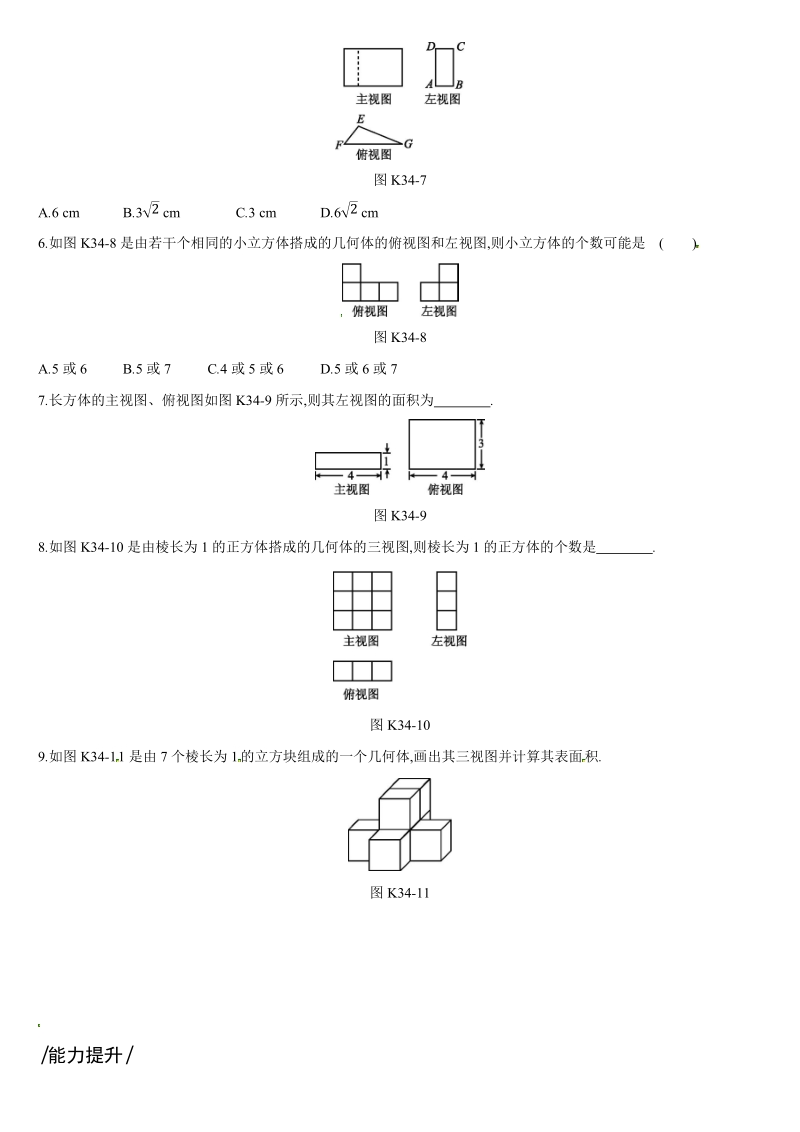
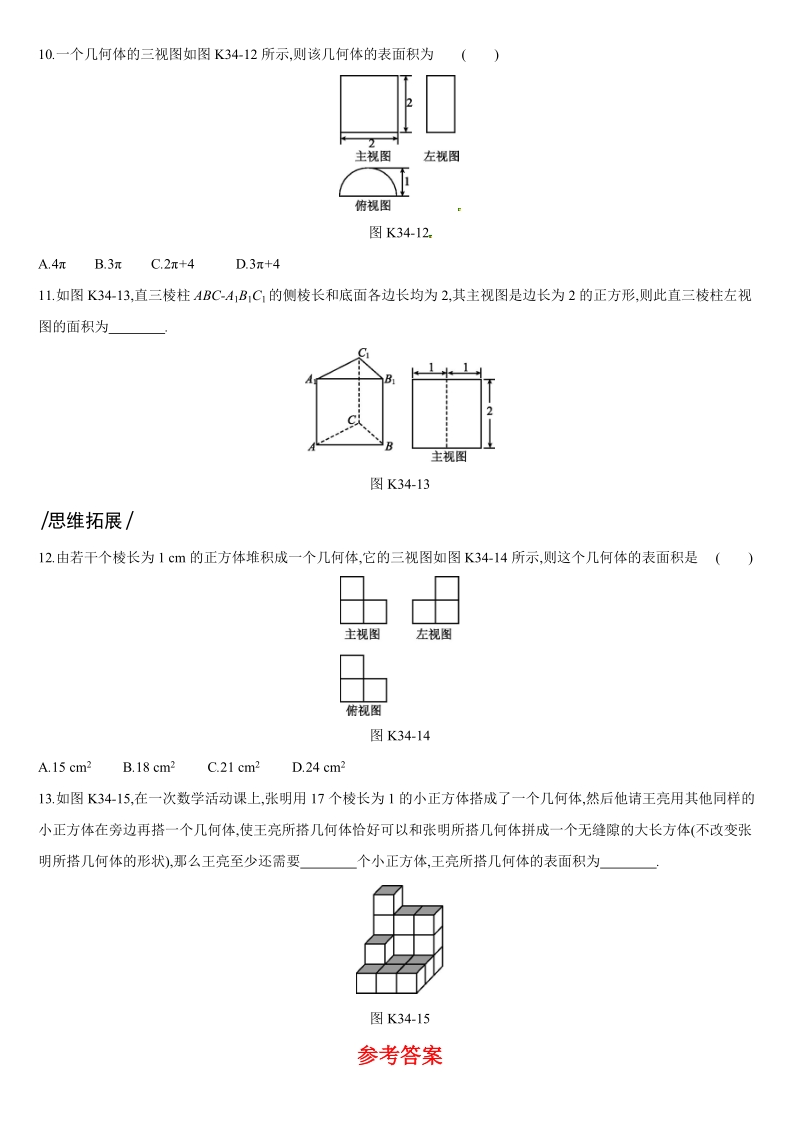
2、6 cm,EFG= 45,则 AB 的长为 ( )图 K34-7A.6 cm B.3 cm C.3 cm D.6 cm2 26.如图 K34-8 是由若干个相同的小立方体搭成的几何体的俯视图和左视图 ,则小立方体的个数可能是 ( )图 K34-8A.5 或 6 B.5 或 7 C.4 或 5 或 6 D.5 或 6 或 77.长方体的主视图、俯视图如图 K34-9 所示,则其左视图的面积为 . 图 K34-98.如图 K34-10 是由棱长为 1 的正方体搭成的几何体的三视图 ,则棱长为 1 的正方体的个数是 . 图 K34-109.如图 K34-11 是由 7 个棱长为 1 的立方块组成的一
3、个几何体 ,画出其三视图并计算其表面 积.图 K34-11|能力提升 |10.一个几何体的三视图如图 K34-12 所示,则该几何体的表面积为 ( )图 K34-12A.4 B.3 C.2+4 D.3+411.如图 K34-13,直三棱柱 ABC-A1B1C1 的侧棱长和底面各边长均为 2,其主视图是边长为 2 的正方形,则此直三棱柱左视图的面积为 . 图 K34-13|思维拓展 |12.由若干个棱长为 1 cm 的正方体堆积成一个几何体,它的三视图如图 K34-14 所示,则这个几何体的表面积是 ( )图 K34-14A.15 cm2 B.18 cm2 C.21 cm2 D.24 cm213
4、.如图 K34-15,在一次数学活动课上,张明用 17 个棱长为 1 的小正方体搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小正方体,王亮所搭几何体的表面积为 . 图 K34-15参考答案1.A 2.C3.B 解析 A.三棱柱的主视图是长方形,左视图是长方形 ,俯视图是三角形,故此选项不符合题意;B.球的主视图、左视图、俯视图都是半径相同的圆,故此选项符合题意;C.圆锥体的主视图是三角形,左视图是三角形 ,俯视图是带圆心的圆,故此 选项不符合题意;D
5、.长方体的主视图是长方形, 左视图是长方形,俯视图是长方形,但是每个长方形的长与宽不完全相同,故此选项 不符合题意.故选 B.4.A 解析 从左面看所得到的图形是长方形,中间带两条竖的虚线.故选 A.5.B6.D 解析 由俯视图易得最底层有 4 个小立方体,由左视图易得第二层最多有 3 个小立方体,最少有 1 个小立方体,那么小立方体的个数可能是 5 或 6 或 7.故选 D.7.3 8.99.解:三视图如下:表面积 S=42+52+52=28.10.D11.2 解析 此直三棱柱左视图为矩形,长边长为 2,短边长为等边三角形 ABC 中 AB 边上的高,为 ,所以此直三棱柱3 3左视图的面积为 2 ,故填 2 .3 312.B 解析 根据主视图、左视图和俯视图可知该几何体由四个正方体组成,各侧面都是 3 个正方形,所以这个几何体的表面积是 36=18(cm2),故选 B.13.19 48 解析 王亮所搭的几何体恰好可以和张明所搭的几何体拼成一个无缝隙的大长方体 ,而搭成 大长方体至少需要小正方体 432=36(个),张明用 17 个棱长为 1 的小 正方体搭成了一个几何体,王亮至少还需 36-17=19(个 )小正方体,表面积为 2(9+7+8)=48,故 填 19 48.
