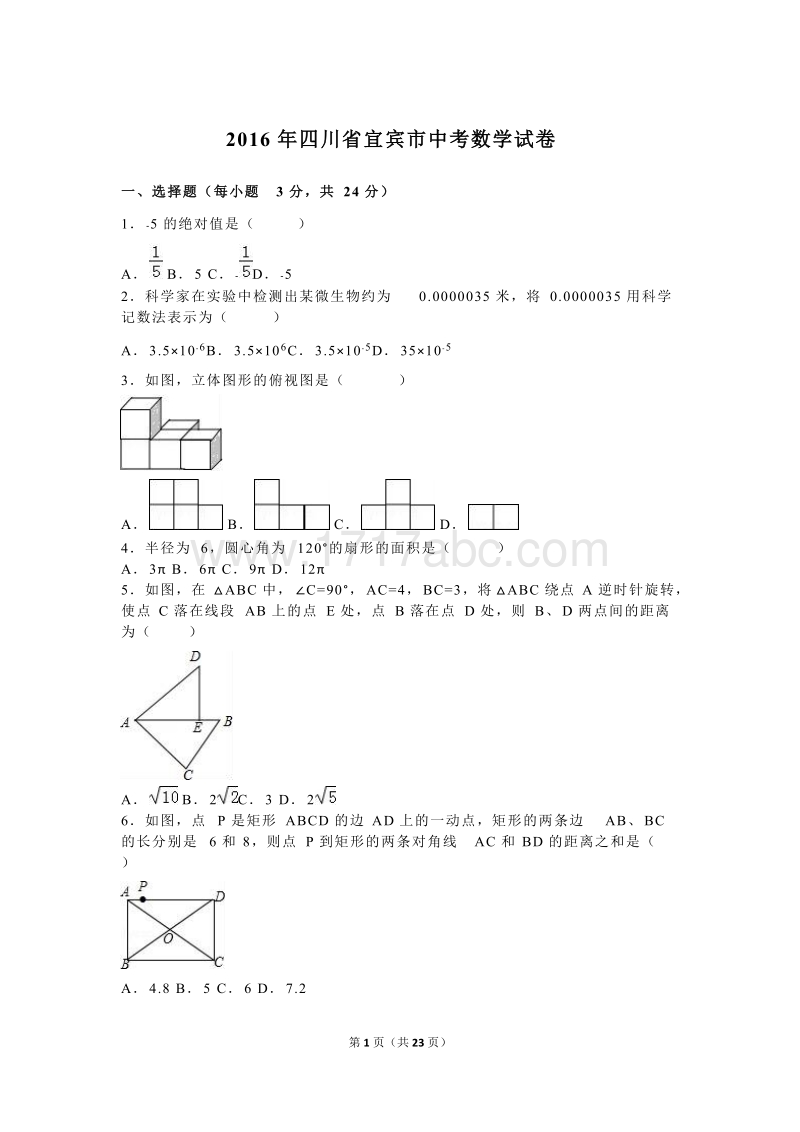
1、第 1 页（共 23 页）2016 年 四 川 省 宜 宾 市 中 考 数 学 试 卷一 、 选 择 题 （ 每 小 题 3 分 ， 共 24 分 ）1 5 的 绝 对 值 是 （ ）A B 5 C D 52 科 学 家 在 实 验 中 检 测 出 某 微 生 物 约 为 0.0000035 米 ， 将 0.0000035 用 科 学记 数 法 表 示 为 （ ）A 3.5106B 3.5106C 3.5105D 351053 如 图 ， 立 体 图 形 的 俯 视 图 是 （ ）A B C D4 半 径 为 6， 圆 心 角 为 120的 扇 形 的 面 积 是 （ ）A 3 B 6 C 9
2、 D 125 如 图 ， 在 ABC 中 ， C=90， AC=4， BC=3， 将 ABC 绕 点 A 逆 时 针 旋 转 ，使 点 C 落 在 线 段 AB 上 的 点 E 处 ， 点 B 落 在 点 D 处 ， 则 B、 D 两 点 间 的 距 离为 （ ）A B 2 C 3 D 26 如 图 ， 点 P 是 矩 形 ABCD 的 边 AD 上 的 一 动 点 ， 矩 形 的 两 条 边 AB、 BC的 长 分 别 是 6 和 8， 则 点 P 到 矩 形 的 两 条 对 角 线 AC 和 BD 的 距 离 之 和 是 （ ）A 4.8 B 5 C 6 D 7.2第 2 页（共 23 页
3、）7 宜 宾 市 某 化 工 厂 ， 现 有 A 种 原 料 52 千 克 ， B 种 原 料 64 千 克 ， 现 用 这 些 原料 生 产 甲 、 乙 两 种 产 品 共 20 件 已 知 生 产 1 件 甲 种 产 品 需 要 A 种 原 料 3 千克 ， B 种 原 料 2 千 克 ； 生 产 1 件 乙 种 产 品 需 要 A 种 原 料 2 千 克 ， B 种 原 料 4千 克 ， 则 生 产 方 案 的 种 数 为 （ ）A 4 B 5 C 6 D 78 如 图 是 甲 、 乙 两 车 在 某 时 段 速 度 随 时 间 变 化 的 图 象 ， 下 列 结 论 错 误 的 是 （
4、 ）A 乙 前 4 秒 行 驶 的 路 程 为 48 米B 在 0 到 8 秒 内 甲 的 速 度 每 秒 增 加 4 米 /秒C 两 车 到 第 3 秒 时 行 驶 的 路 程 相 等D 在 4 至 8 秒 内 甲 的 速 度 都 大 于 乙 的 速 度二 、 填 空 题 （ 每 小 题 3 分 ， 共 24 分 ）9 分 解 因 式 ： ab44ab3+4ab2= 10 如 图 ， 直 线 ab， 1=45， 2=30， 则 P= 11 已 知 一 组 数 据 ： 3， 3， 4， 7， 8， 则 它 的 方 差 为 12 今 年 “五 一 ”节 ， A、 B 两 人 到 商 场 购 物
5、， A 购 3 件 甲 商 品 和 2 件 乙 商 品 共支 付 16 元 ， B 购 5 件 甲 商 品 和 3 件 乙 商 品 共 支 付 25 元 ， 求 一 件 甲 商 品 和 一 件乙 商 品 各 售 多 少 元 设 甲 商 品 售 价 x 元 /件 ， 乙 商 品 售 价 y 元 /件 ， 则 可 列 出 方程 组 13 在 平 面 直 角 坐 标 系 内 ， 以 点 P（ 1， 1） 为 圆 心 、 为 半 径 作 圆 ， 则 该 圆 与y 轴 的 交 点 坐 标 是 14 已 知 一 元 二 次 方 程 x2+3x4=0 的 两 根 为 x1、 x2， 则 x12+x1x2+x
6、22= 15 规 定 ： logab（ a 0， a1， b 0） 表 示 a， b 之 间 的 一 种 运 算 现 有 如 下 的 运 算 法 则 ：lognan=n logNM= （ a 0， a1， N 0， N1， M 0） 例 如 ： log223=3， log25= ， 则 log1001000= 第 3 页（共 23 页）16 如 图 ， 在 边 长 为 4 的 正 方 形 ABCD 中 ， P 是 BC 边 上 一 动 点 （ 不 含B、 C 两 点 ） ， 将 ABP 沿 直 线 AP 翻 折 ， 点 B 落 在 点 E 处 ； 在 CD 上 有 一 点M， 使 得 将 CM
7、P 沿 直 线 MP 翻 折 后 ， 点 C 落 在 直 线 PE 上 的 点 F 处 ， 直 线PE 交 CD 于 点 N， 连 接 MA， NA 则 以 下 结 论 中 正 确 的 有 （ 写出 所 有 正 确 结 论 的 序 号 ）CMPBPA；四 边 形 AMCB 的 面 积 最 大 值 为 10；当 P 为 BC 中 点 时 ， AE 为 线 段 NP 的 中 垂 线 ；线 段 AM 的 最 小 值 为 2 ；当 ABPADN 时 ， BP=4 4三 、 解 答 题 （ 本 大 题 共 8 小 题 ， 共 72 分 ）17 （ 1） 计 算 ； （ ） 2（ 1） 2016 +（ 1
8、） 0（ 2） 化 简 ： （ 1 ）18 如 图 ， 已 知 CAB=DBA， CBD=DAC求 证 ： BC=AD19 某 校 要 求 八 年 级 同 学 在 课 外 活 动 中 ， 必 须 在 五 项 球 类 （ 篮 球 、 足 球 、 排 球 、 羽毛 球 、 乒 乓 球 ） 活 动 中 任 选 一 项 （ 只 能 选 一 项 ） 参 加 训 练 ， 为 了 了 解 八 年 级 学 生 参加 球 类 活 动 的 整 体 情 况 ， 现 以 八 年 级 2 班 作 为 样 本 ， 对 该 班 学 生 参 加 球 类 活 动的 情 况 进 行 统 计 ， 并 绘 制 了 如 图 所 示 的
9、 不 完 整 统 计 表 和 扇 形 统 计 图 ：八 年 级 2 班 参 加 球 类 活 动 人 数 统 计 表项 目 篮 球 足 球 乒 乓 球 排 球 羽 毛 球人 数 a 6 5 7 6根 据 图 中 提 供 的 信 息 ， 解 答 下 列 问 题 ：（ 1） a= ， b= ；（ 2） 该 校 八 年 级 学 生 共 有 600 人 ， 则 该 年 级 参 加 足 球 活 动 的 人 数 约 人 ；第 4 页（共 23 页）（ 3） 该 班 参 加 乒 乓 球 活 动 的 5 位 同 学 中 ， 有 3 位 男 同 学 （ A， B， C） 和 2位 女 同 学 （ D， E） ，
10、现 准 备 从 中 选 取 两 名 同 学 组 成 双 打 组 合 ， 用 树 状 图 或 列 表 法求 恰 好 选 出 一 男 一 女 组 成 混 合 双 打 组 合 的 概 率 20 2016 年 “母 亲 节 ”前 夕 ， 宜 宾 某 花 店 用 4000 元 购 进 若 干 束 花 ， 很 快 售 完 ，接 着 又 用 4500 元 购 进 第 二 批 花 ， 已 知 第 二 批 所 购 花 的 束 数 是 第 一 批 所 购 花 束 数 的1.5 倍 ， 且 每 束 花 的 进 价 比 第 一 批 的 进 价 少 5 元 ， 求 第 一 批 花 每 束 的 进 价 是 多少 ？21
11、如 图 ， CD 是 一 高 为 4 米 的 平 台 ， AB 是 与 CD 底 部 相 平 的 一 棵 树 ， 在 平 台顶 C 点 测 得 树 顶 A 点 的 仰 角 =30， 从 平 台 底 部 向 树 的 方 向 水 平 前 进 3 米 到达 点 E， 在 点 E 处 测 得 树 顶 A 点 的 仰 角 =60， 求 树 高 AB（ 结 果 保 留 根 号 ）22 如 图 ， 一 次 函 数 y=kx+b 的 图 象 与 反 比 例 函 数 y= （ x 0） 的 图 象 交 于A（ 2， 1） ， B（ ， n） 两 点 ， 直 线 y=2 与 y 轴 交 于 点 C（ 1） 求 一
12、 次 函 数 与 反 比 例 函 数 的 解 析 式 ；（ 2） 求 ABC 的 面 积 23 如 图 1， 在 APE 中 ， PAE=90， PO 是 APE 的 角 平 分 线 ， 以 O 为 圆 心 ，OA 为 半 径 作 圆 交 AE 于 点 G（ 1） 求 证 ： 直 线 PE 是 O 的 切 线 ；（ 2） 在 图 2 中 ， 设 PE 与 O 相 切 于 点 H， 连 结 AH， 点 D 是 O 的 劣 弧上 一 点 ， 过 点 D 作 O 的 切 线 ， 交 PA 于 点 B， 交 PE 于 点 C， 已 知 PBC的 周 长 为 4， tanEAH= ， 求 EH 的 长
13、第 5 页（共 23 页）24 如 图 ， 已 知 二 次 函 数 y1=ax2+bx 过 （ 2， 4） ， （ 4， 4） 两 点 （ 1） 求 二 次 函 数 y1 的 解 析 式 ；（ 2） 将 y1 沿 x 轴 翻 折 ， 再 向 右 平 移 2 个 单 位 ， 得 到 抛 物 线 y2， 直 线y=m（ m 0） 交 y2 于 M、 N 两 点 ， 求 线 段 MN 的 长 度 （ 用 含 m 的 代 数 式 表 示 ）；（ 3） 在 （ 2） 的 条 件 下 ， y1、 y2 交 于 A、 B 两 点 ， 如 果 直 线 y=m 与 y1、 y2的 图 象 形 成 的 封 闭 曲
14、 线 交 于 C、 D 两 点 （ C 在 左 侧 ） ， 直 线 y=m 与 y1、 y2 的图 象 形 成 的 封 闭 曲 线 交 于 E、 F 两 点 （ E 在 左 侧 ） ， 求 证 ： 四 边 形 CEFD 是 平行 四 边 形 第 6 页（共 23 页）2016 年 四 川 省 宜 宾 市 中 考 数 学 试 卷参 考 答 案 与 试 题 解 析一 、 选 择 题 （ 每 小 题 3 分 ， 共 24 分 ）1 5 的 绝 对 值 是 （ ）A B 5 C D 5【 考 点 】 绝 对 值 【 分 析 】 绝 对 值 的 性 质 ： 一 个 正 数 的 绝 对 值 是 它 本 身
15、 ； 一 个 负 数 的 绝 对 值 是 它 的相 反 数 ； 0 的 绝 对 值 是 0【 解 答 】 解 ： 根 据 负 数 的 绝 对 值 是 它 的 相 反 数 ， 得 |5|=5故 选 ： B2 科 学 家 在 实 验 中 检 测 出 某 微 生 物 约 为 0.0000035 米 ， 将 0.0000035 用 科 学记 数 法 表 示 为 （ ）A 3.5106B 3.5106C 3.5105D 35105【 考 点 】 科 学 记 数 法 表 示 较 小 的 数 【 分 析 】 绝 对 值 小 于 1 的 正 数 也 可 以 利 用 科 学 记 数 法 表 示 ， 一 般 形
16、式 为a10n， 与 较 大 数 的 科 学 记 数 法 不 同 的 是 其 所 使 用 的 是 负 指 数 幂 ， 指 数 由 原 数 左 边起 第 一 个 不 为 零 的 数 字 前 面 的 0 的 个 数 所 决 定 【 解 答 】 解 ： 0.0000035=3.5106，故 选 ： A3 如 图 ， 立 体 图 形 的 俯 视 图 是 （ ）A B C D【 考 点 】 简 单 组 合 体 的 三 视 图 【 分 析 】 根 据 几 何 体 的 三 视 图 ， 即 可 解 答 【 解 答 】 解 ： 立 体 图 形 的 俯 视 图 是 C故 选 ： C4 半 径 为 6， 圆 心 角
17、 为 120的 扇 形 的 面 积 是 （ ）第 7 页（共 23 页）A 3 B 6 C 9 D 12【 考 点 】 扇 形 面 积 的 计 算 【 分 析 】 根 据 扇 形 的 面 积 公 式 S= 计 算 即 可 【 解 答 】 解 ： S= =12，故 选 ： D5 如 图 ， 在 ABC 中 ， C=90， AC=4， BC=3， 将 ABC 绕 点 A 逆 时 针 旋 转 ，使 点 C 落 在 线 段 AB 上 的 点 E 处 ， 点 B 落 在 点 D 处 ， 则 B、 D 两 点 间 的 距 离为 （ ）A B 2 C 3 D 2【 考 点 】 旋 转 的 性 质 【 分 析
18、 】 通 过 勾 股 定 理 计 算 出 AB 长 度 ， 利 用 旋 转 性 质 求 出 各 对 应 线 段 长 度 ， 利用 勾 股 定 理 求 出 B、 D 两 点 间 的 距 离 【 解 答 】 解 ： 在 ABC 中 ， C=90， AC=4， BC=3，AB=5，将 ABC 绕 点 A 逆 时 针 旋 转 ， 使 点 C 落 在 线 段 AB 上 的 点 E 处 ， 点 B 落 在点 D 处 ，AE=4， DE=3，BE=1，在 RtBED 中 ，BD= = 故 选 ： A6 如 图 ， 点 P 是 矩 形 ABCD 的 边 AD 上 的 一 动 点 ， 矩 形 的 两 条 边 A
19、B、 BC的 长 分 别 是 6 和 8， 则 点 P 到 矩 形 的 两 条 对 角 线 AC 和 BD 的 距 离 之 和 是 （ ）A 4.8 B 5 C 6 D 7.2第 8 页（共 23 页）【 考 点 】 矩 形 的 性 质 【 分 析 】 首 先 连 接 OP， 由 矩 形 的 两 条 边 AB、 BC 的 长 分 别 为 3 和 4， 可 求 得OA=OD=5， AOD 的 面 积 ， 然 后 由 SAOD=SAOP+SDOP= OAPE+ODPF求 得 答 案 【 解 答 】 解 ： 连 接 OP，矩 形 的 两 条 边 AB、 BC 的 长 分 别 为 6 和 8，S 矩
20、形 ABCD=ABBC=48， OA=OC， OB=OD， AC=BD=10，OA=OD=5，SACD= S 矩 形 ABCD=24，SAOD= SACD=12，SAOD=SAOP+SDOP= OAPE+ ODPF= 5PE+ 5PF= （ PE+PF）=12，解 得 ： PE+PF=4.8故 选 ： A7 宜 宾 市 某 化 工 厂 ， 现 有 A 种 原 料 52 千 克 ， B 种 原 料 64 千 克 ， 现 用 这 些 原料 生 产 甲 、 乙 两 种 产 品 共 20 件 已 知 生 产 1 件 甲 种 产 品 需 要 A 种 原 料 3 千克 ， B 种 原 料 2 千 克 ；
21、生 产 1 件 乙 种 产 品 需 要 A 种 原 料 2 千 克 ， B 种 原 料 4千 克 ， 则 生 产 方 案 的 种 数 为 （ ）A 4 B 5 C 6 D 7【 考 点 】 二 元 一 次 方 程 组 的 应 用 【 分 析 】 设 生 产 甲 产 品 x 件 ， 则 乙 产 品 （ 20x） 件 ， 根 据 生 产 1 件 甲 种 产 品 需要 A 种 原 料 3 千 克 ， B 种 原 料 2 千 克 ； 生 产 1 件 乙 种 产 品 需 要 A 种 原 料 2 千克 ， B 种 原 料 4 千 克 ， 列 出 不 等 式 组 ， 求 出 不 等 式 组 的 解 ， 再
22、根 据 x 为 整 数 ，得 出 有 5 种 生 产 方 案 【 解 答 】 解 ： 设 生 产 甲 产 品 x 件 ， 则 乙 产 品 （ 20x） 件 ， 根 据 题 意 得 ：，解 得 ： 8x12，x 为 整 数 ，x=8， 9， 10， 11， 12，第 9 页（共 23 页）有 5 种 生 产 方 案 ：方 案 1， A 产 品 8 件 ， B 产 品 12 件 ；方 案 2， A 产 品 9 件 ， B 产 品 11 件 ；方 案 3， A 产 品 10 件 ， B 产 品 10 件 ；方 案 4， A 产 品 11 件 ， B 产 品 9 件 ；方 案 5， A 产 品 12
23、件 ， B 产 品 8 件 ；故 选 B8 如 图 是 甲 、 乙 两 车 在 某 时 段 速 度 随 时 间 变 化 的 图 象 ， 下 列 结 论 错 误 的 是 （ ）A 乙 前 4 秒 行 驶 的 路 程 为 48 米B 在 0 到 8 秒 内 甲 的 速 度 每 秒 增 加 4 米 /秒C 两 车 到 第 3 秒 时 行 驶 的 路 程 相 等D 在 4 至 8 秒 内 甲 的 速 度 都 大 于 乙 的 速 度【 考 点 】 函 数 的 图 象 【 分 析 】 根 据 函 数 图 象 和 速 度 、 时 间 、 路 程 之 间 的 关 系 ， 分 别 对 每 一 项 进 行 分 析
24、即 可 得 出 答 案 【 解 答 】 解 ： A、 根 据 图 象 可 得 ， 乙 前 4 秒 行 驶 的 路 程 为 124=48 米 ， 正 确 ；B、 根 据 图 象 得 ： 在 0 到 8 秒 内 甲 的 速 度 每 秒 增 加 4 米 秒 /， 正 确 ；C、 根 据 图 象 可 得 两 车 到 第 3 秒 时 行 驶 的 路 程 不 相 等 ， 故 本 选 项 错 误 ；D、 在 4 至 8 秒 内 甲 的 速 度 都 大 于 乙 的 速 度 ， 正 确 ；故 选 C二 、 填 空 题 （ 每 小 题 3 分 ， 共 24 分 ）9 分 解 因 式 ： ab44ab3+4ab2=
25、 ab2（ b2） 2 【 考 点 】 提 公 因 式 法 与 公 式 法 的 综 合 运 用 【 分 析 】 此 多 项 式 有 公 因 式 ， 应 先 提 取 公 因 式 ， 再 对 余 下 的 多 项 式 进 行 观 察 ， 有 3项 ， 可 采 用 完 全 平 方 公 式 继 续 分 解 【 解 答 】 解 ： ab44ab3+4ab2=ab2（ b24b+4）=ab2（ b2） 2故 答 案 为 ： ab2（ b2） 210 如 图 ， 直 线 ab， 1=45， 2=30， 则 P= 75 第 10 页（共 23 页）【 考 点 】 平 行 线 的 性 质 【 分 析 】 过 P
26、作 PM直 线 a， 求 出 直 线 abPM， 根 据 平 行 线 的 性 质 得 出EPM=2=30， FPM=1=45， 即 可 求 出 答 案 【 解 答 】 解 ：过 P 作 PM直 线 a，直 线 ab，直 线 abPM，1=45， 2=30，EPM=2=30， FPM=1=45，EPF=EPM+FPM=30+45=75，故 答 案 为 ： 7511 已 知 一 组 数 据 ： 3， 3， 4， 7， 8， 则 它 的 方 差 为 4.4 【 考 点 】 方 差 【 分 析 】 根 据 平 均 数 的 计 算 公 式 先 算 出 这 组 数 据 的 平 均 数 ， 再 根 据 方
27、差 公 式 进 行计 算 即 可 【 解 答 】 解 ： 这 组 数 据 的 平 均 数 是 ： （ 3+3+4+7+8） 5=5，则 这 组 数 据 的 方 差 为 ： （ 35） 2+（ 35） 2+（ 45） 2+（ 75） 2+（ 85） 2=4.4故 答 案 为 ： 4.412 今 年 “五 一 ”节 ， A、 B 两 人 到 商 场 购 物 ， A 购 3 件 甲 商 品 和 2 件 乙 商 品 共支 付 16 元 ， B 购 5 件 甲 商 品 和 3 件 乙 商 品 共 支 付 25 元 ， 求 一 件 甲 商 品 和 一 件乙 商 品 各 售 多 少 元 设 甲 商 品 售
28、价 x 元 /件 ， 乙 商 品 售 价 y 元 /件 ， 则 可 列 出 方程 组 【 考 点 】 由 实 际 问 题 抽 象 出 二 元 一 次 方 程 组 【 分 析 】 分 别 利 用 “A 购 3 件 甲 商 品 和 2 件 乙 商 品 共 支 付 16 元 ， B 购 5 件 甲商 品 和 3 件 乙 商 品 共 支 付 25 元 ”得 出 等 式 求 出 答 案 【 解 答 】 解 ： 设 甲 商 品 售 价 x 元 /件 ， 乙 商 品 售 价 y 元 /件 ， 则 可 列 出 方 程 组 ：故 答 案 为 ： 第 11 页（共 23 页）13 在 平 面 直 角 坐 标 系
29、内 ， 以 点 P（ 1， 1） 为 圆 心 、 为 半 径 作 圆 ， 则 该 圆 与y 轴 的 交 点 坐 标 是 （ 0， 3） ， （ 0， 1） 【 考 点 】 坐 标 与 图 形 性 质 【 分 析 】 在 平 面 直 角 坐 标 系 中 ， 根 据 勾 股 定 理 先 求 出 直 角 三 角 形 的 另 外 一 个 直 角边 ， 再 根 据 点 P 的 坐 标 即 可 得 出 答 案 【 解 答 】 解 ： 以 （ 1， 1） 为 圆 心 ， 为 半 径 画 圆 ， 与 y 轴 相 交 ， 构 成 直 角 三 角形 ，用 勾 股 定 理 计 算 得 另 一 直 角 边 的 长 为
30、 2，则 与 y 轴 交 点 坐 标 为 （ 0， 3） 或 （ 0， 1） 故 答 案 为 ： （ 0， 3） ， （ 0， 1） 14 已 知 一 元 二 次 方 程 x2+3x4=0 的 两 根 为 x1、 x2， 则 x12+x1x2+x22= 13 【 考 点 】 根 与 系 数 的 关 系 【 分 析 】 根 据 根 与 系 数 的 关 系 得 到 x1+x2=3， x1x2=4， 再 利 用 完 全 平 方 公 式 变形 得 到 x12+x1x2+x22=（ x1+x2） 2x1x2， 然 后 利 用 整 体 代 入 的 方 法 计 算 【 解 答 】 解 ： 根 据 题 意 得
31、 x1+x2=3， x1x2=4，所 以 x12+x1x2+x22=（ x1+x2） 2x1x2=（ 3） 2（ 4） =13故 答 案 为 1315 规 定 ： logab（ a 0， a1， b 0） 表 示 a， b 之 间 的 一 种 运 算 现 有 如 下 的 运 算 法 则 ：lognan=n logNM= （ a 0， a1， N 0， N1， M 0） 例 如 ： log223=3， log25= ， 则 log1001000= 【 考 点 】 实 数 的 运 算 【 分 析 】 先 根 据 logNM= （ a 0， a1， N 0， N1， M 0） 将 所 求 式子 化
32、成 以 10 为 底 的 对 数 形 式 ， 再 利 用 公 式 进 行 计 算 第 12 页（共 23 页）【 解 答 】 解 ： log1001000= = = 故 答 案 为 ： 16 如 图 ， 在 边 长 为 4 的 正 方 形 ABCD 中 ， P 是 BC 边 上 一 动 点 （ 不 含B、 C 两 点 ） ， 将 ABP 沿 直 线 AP 翻 折 ， 点 B 落 在 点 E 处 ； 在 CD 上 有 一 点M， 使 得 将 CMP 沿 直 线 MP 翻 折 后 ， 点 C 落 在 直 线 PE 上 的 点 F 处 ， 直 线PE 交 CD 于 点 N， 连 接 MA， NA 则
33、 以 下 结 论 中 正 确 的 有 （ 写出 所 有 正 确 结 论 的 序 号 ）CMPBPA；四 边 形 AMCB 的 面 积 最 大 值 为 10；当 P 为 BC 中 点 时 ， AE 为 线 段 NP 的 中 垂 线 ；线 段 AM 的 最 小 值 为 2 ；当 ABPADN 时 ， BP=4 4【 考 点 】 相 似 形 综 合 题 【 分 析 】 正 确 ， 只 要 证 明 APM=90即 可 解 决 问 题 正 确 ， 设 PB=x， 构 建 二 次 函 数 ， 利 用 二 次 函 数 性 质 解 决 问 题 即 可 错 误 ， 设 ND=NE=y， 在 RTPCN 中 ，
34、利 用 勾 股 定 理 求 出 y 即 可 解 决 问题 错 误 ， 作 MGAB 于 G， 因 为 AM= = ， 所 以 AG 最 小 时AM 最 小 ， 构 建 二 次 函 数 ， 求 得 AG 的 最 小 值 为 3， AM 的 最 小 值 为 5正 确 ， 在 AB 上 取 一 点 K 使 得 AK=PK， 设 PB=z， 列 出 方 程 即 可 解 决 问 题 【 解 答 】 解 ： APB=APE， MPC=MPN，CPN+NPB=180，2NPM+2APE=180，MPN+APE=90，APM=90，CPM+APB=90， APB+PAB=90，CPM=PAB，四 边 形 AB
35、CD 是 正 方 形 ，AB=CB=DC=AD=4， C=B=90，CMPBPA 故 正 确 ，设 PB=x， 则 CP=4x，第 13 页（共 23 页）CMPBPA， = ，CM= x（ 4x） ，S 四 边 形 AMCB= 4+ x（ 4x） 4= x2+2x+8= （ x2） 2+10，x=2 时 ， 四 边 形 AMCB 面 积 最 大 值 为 10， 故 正 确 ，当 PB=PC=PE=2 时 ， 设 ND=NE=y，在 RTPCN 中 ， （ y+2） 2=（ 4y） 2+22 解 得 y= ，NEEP， 故 错 误 ，作 MGAB 于 G，AM= = ，AG 最 小 时 AM
36、最 小 ，AG=ABBG=ABCM=4 x（ 4x） = （ x1） 2+3，x=1 时 ， AG 最 小 值 =3，AM 的 最 小 值 = =5， 故 错 误 ABPADN 时 ，PAB=DAN=22.5， 在 AB 上 取 一 点 K 使 得 AK=PK， 设 PB=z，KPA=KAP=22.5PKB=KPA+KAP=45，BPK=BKP=45，PB=BK=z， AK=PK= z，z+ z=4，z=4 4，PB=4 4 故 正 确 故 答 案 为 三 、 解 答 题 （ 本 大 题 共 8 小 题 ， 共 72 分 ）17 （ 1） 计 算 ； （ ） 2（ 1） 2016 +（ 1）
37、0第 14 页（共 23 页）（ 2） 化 简 ： （ 1 ）【 考 点 】 实 数 的 运 算 ； 分 式 的 混 合 运 算 ； 零 指 数 幂 ； 负 整 数 指 数 幂 【 分 析 】 （ 1） 原 式 利 用 零 指 数 幂 、 负 整 数 指 数 幂 法 则 ， 乘 方 的 意 义 ， 以 及 算 术 平方 根 定 义 计 算 即 可 得 到 结 果 ；（ 2） 原 式 括 号 中 两 项 通 分 并 利 用 同 分 母 分 式 的 减 法 法 则 计 算 ， 同 时 利 用 除 法 法 则变 形 ， 约 分 即 可 得 到 结 果 【 解 答 】 解 ： （ 1） 原 式 =91
38、5+1=4；（ 2） 原 式 = = = 18 如 图 ， 已 知 CAB=DBA， CBD=DAC求 证 ： BC=AD【 考 点 】 全 等 三 角 形 的 判 定 与 性 质 【 分 析 】 先 根 据 题 意 得 出 DAB=CBA， 再 由 ASA 定 理 可 得 出 ADBBCA， 由 此 可 得 出 结 论 【 解 答 】 解 ： CAB=DBA， CBD=DAC，DAB=CBA在 ADB 与 BCA 中 ，ADBBCA（ ASA） ，BC=AD19 某 校 要 求 八 年 级 同 学 在 课 外 活 动 中 ， 必 须 在 五 项 球 类 （ 篮 球 、 足 球 、 排 球 、
39、 羽毛 球 、 乒 乓 球 ） 活 动 中 任 选 一 项 （ 只 能 选 一 项 ） 参 加 训 练 ， 为 了 了 解 八 年 级 学 生 参加 球 类 活 动 的 整 体 情 况 ， 现 以 八 年 级 2 班 作 为 样 本 ， 对 该 班 学 生 参 加 球 类 活 动的 情 况 进 行 统 计 ， 并 绘 制 了 如 图 所 示 的 不 完 整 统 计 表 和 扇 形 统 计 图 ：八 年 级 2 班 参 加 球 类 活 动 人 数 统 计 表项 目 篮 球 足 球 乒 乓 球 排 球 羽 毛 球人 数 a 6 5 7 6根 据 图 中 提 供 的 信 息 ， 解 答 下 列 问
40、题 ：（ 1） a= 16 ， b= 17.5 ；第 15 页（共 23 页）（ 2） 该 校 八 年 级 学 生 共 有 600 人 ， 则 该 年 级 参 加 足 球 活 动 的 人 数 约 90 人 ；（ 3） 该 班 参 加 乒 乓 球 活 动 的 5 位 同 学 中 ， 有 3 位 男 同 学 （ A， B， C） 和 2位 女 同 学 （ D， E） ， 现 准 备 从 中 选 取 两 名 同 学 组 成 双 打 组 合 ， 用 树 状 图 或 列 表 法求 恰 好 选 出 一 男 一 女 组 成 混 合 双 打 组 合 的 概 率 【 考 点 】 列 表 法 与 树 状 图 法
41、； 用 样 本 估 计 总 体 ； 扇 形 统 计 图 【 分 析 】 （ 1） 首 先 求 得 总 人 数 ， 然 后 根 据 百 分 比 的 定 义 求 解 ；（ 2） 利 用 总 数 乘 以 对 应 的 百 分 比 即 可 求 解 ；（ 3） 利 用 列 举 法 ， 根 据 概 率 公 式 即 可 求 解 【 解 答 】 解 ： （ 1） a=512.5%40%=16， 512.5%=7b%，b=17.5，故 答 案 为 ： 16， 17.5；（ 2） 6006（ 512.5%） =90（ 人 ） ，故 答 案 为 ： 90；（ 3） 如 图 ， 共 有 20 种 等 可 能 的 结 果
42、 ， 两 名 主 持 人 恰 为 一 男 一 女 的 有 12 种情 况 ，则 P（ 恰 好 选 到 一 男 一 女 ） = = 20 2016 年 “母 亲 节 ”前 夕 ， 宜 宾 某 花 店 用 4000 元 购 进 若 干 束 花 ， 很 快 售 完 ，接 着 又 用 4500 元 购 进 第 二 批 花 ， 已 知 第 二 批 所 购 花 的 束 数 是 第 一 批 所 购 花 束 数 的1.5 倍 ， 且 每 束 花 的 进 价 比 第 一 批 的 进 价 少 5 元 ， 求 第 一 批 花 每 束 的 进 价 是 多少 ？【 考 点 】 分 式 方 程 的 应 用 【 分 析 】
43、 设 第 一 批 花 每 束 的 进 价 是 x 元 /束 ， 则 第 一 批 进 的 数 量 是 ： ， 第二 批 进 的 数 量 是 ： ， 再 根 据 等 量 关 系 ： 第 二 批 进 的 数 量 =第 一 批 进 的 数 量1.5 可 得 方 程 【 解 答 】 解 ： 设 第 一 批 花 每 束 的 进 价 是 x 元 /束 ，依 题 意 得 ： 1.5= ，第 16 页（共 23 页）解 得 x=20经 检 验 x=20 是 原 方 程 的 解 ， 且 符 合 题 意 答 ： 第 一 批 花 每 束 的 进 价 是 20 元 /束 21 如 图 ， CD 是 一 高 为 4 米
44、的 平 台 ， AB 是 与 CD 底 部 相 平 的 一 棵 树 ， 在 平 台顶 C 点 测 得 树 顶 A 点 的 仰 角 =30， 从 平 台 底 部 向 树 的 方 向 水 平 前 进 3 米 到达 点 E， 在 点 E 处 测 得 树 顶 A 点 的 仰 角 =60， 求 树 高 AB（ 结 果 保 留 根 号 ）【 考 点 】 解 直 角 三 角 形 的 应 用 -仰 角 俯 角 问 题 【 分 析 】 作 CFAB 于 点 F， 设 AF=x 米 ， 在 直 角 ACF 中 利 用 三 角 函 数 用 x表 示 出 CF 的 长 ， 在 直 角 ABE 中 表 示 出 BE 的
45、 长 ， 然 后 根 据 CFBE=DE 即 可列 方 程 求 得 x 的 值 ， 进 而 求 得 AB 的 长 【 解 答 】 解 ： 作 CFAB 于 点 F， 设 AF=x 米 ，在 RtACF 中 ， tanACF= ，则 CF= = = = x，在 直 角 ABE 中 ， AB=x+BF=4+x（ 米 ） ，在 直 角 ABF 中 ， tanAEB= ， 则 BE= = = （ x+4） 米 CFBE=DE， 即 x （ x+4） =3解 得 ： x= ，则 AB= +4= （ 米 ） 答 ： 树 高 AB 是 米 第 17 页（共 23 页）22 如 图 ， 一 次 函 数 y=k
46、x+b 的 图 象 与 反 比 例 函 数 y= （ x 0） 的 图 象 交 于A（ 2， 1） ， B（ ， n） 两 点 ， 直 线 y=2 与 y 轴 交 于 点 C（ 1） 求 一 次 函 数 与 反 比 例 函 数 的 解 析 式 ；（ 2） 求 ABC 的 面 积 【 考 点 】 反 比 例 函 数 与 一 次 函 数 的 交 点 问 题 【 分 析 】 （ 1） 把 A 坐 标 代 入 反 比 例 解 析 式 求 出 m 的 值 ， 确 定 出 反 比 例 解 析 式 ，再 将 B 坐 标 代 入 求 出 n 的 值 ， 确 定 出 B 坐 标 ， 将 A 与 B 坐 标 代 入 一 次 函 数 解析 式 求 出 k 与 b 的 值 ， 即 可 确 定 出 一 次 函 数 解 析 式 ；（ 2） 利 用 两 点 间 的 距 离 公 式 求 出 AB 的 长 ， 利 用 点 到 直 线 的 距 离 公 式 求 出 点 C到 直 线 AB 的 距 离 ， 即 可 确 定 出 三 角 形 ABC 面 积 【 解 答 】 解 ： （ 1） 把 A（ 2， 1） 代 入 反 比 例 解 析 式 得 ： 1= ， 即 m=2，反 比 例 解 析 式 为 y= ，把 B（ ， n） 代 入 反 比 例 解 析 式 得 ： n=4， 即 B（ ， 4
