1、 期末复习：人教版九年级数学下册 第 28 章 锐角三角函数 单元检测试卷一、单选题（共 10 题；共 30 分）1.sin60的值为（ ） A. B. C. D. 332 22 122.在ABC 中， C =90o ， 若 cosB= ，则B 的值为（ ） 32A. B. C. D. 30 60 45 903.在 RtABC 中， C=90，AB=13，AC=5 ，则 sinA 的值为（ ） A. B. C. D. 513 1213 512 1254.在 中， ， ，则 的值等于（ ） ABC C=90AC=BC sinAA. B. C. D. 12 22 32 15.在 ABC 中， C
2、90， AC 9， sinB ，则 AB( ) 35A. 15 B. 12 C. 9 D. 66.一个物体从 A 点出发，沿坡度为 1：7 的斜坡向上直线运动到 B，AB=30 米时，物体升高（ ）米 A. B. 3 C. D. 以上的答案都不对307 2 3067.如图，在ABC 中， ACB=90，ABC=26，BC=5若用科学计算器求边 AC 的长，则下列按键顺序正确的是（ ）A. 5tan26= B. 5sin26= C. 5cos26= D. 5tan26=8.在ABC 中，若|sinA |+（ cosB） 2=0，则C 的度数是（ ） 12 22A. 45 B. 75 C. 105
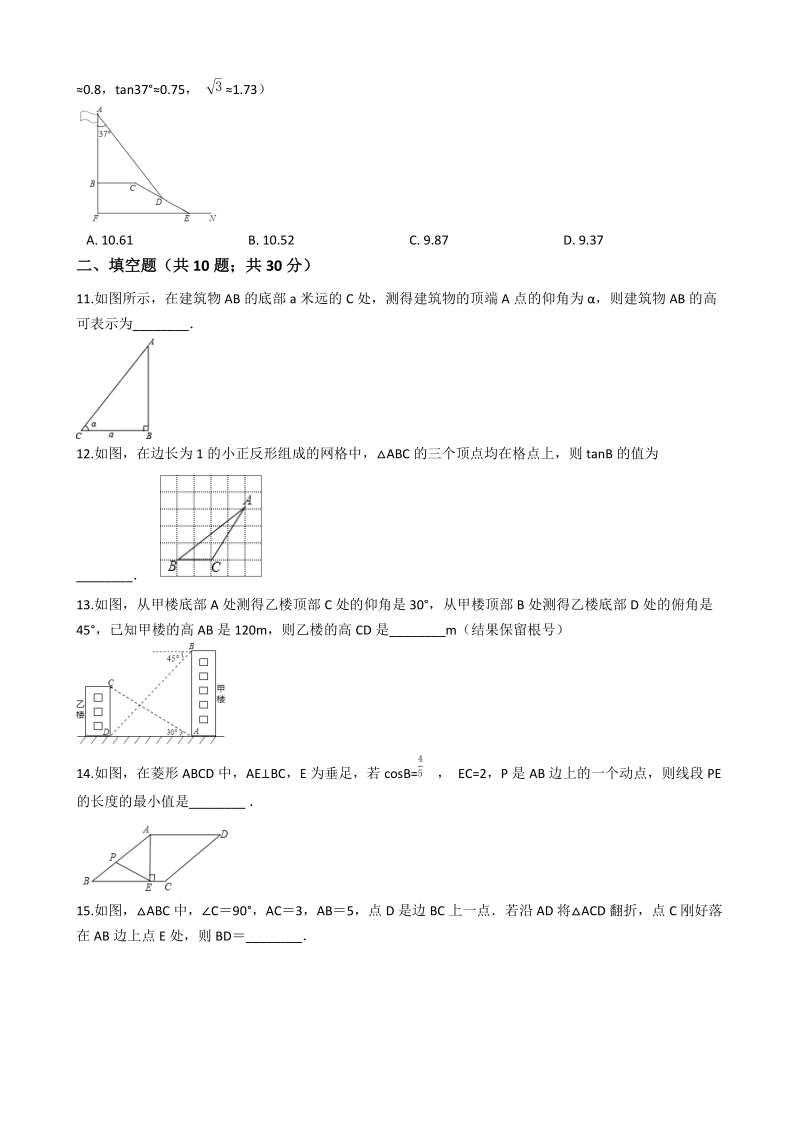
3、 D. 1209.在 中， ， ， ，则 cosA 等于（ ） RtABC C=90a=5 b=12A. B. C. D. 512 513 125 121310.在学习解直角三角形以后，重庆八中数学兴趣小组测量了旗杆的高度如图，某一时刻，旗杆 AB 的影子一部分落在平台上的影长 BC 为 6 米，落在斜坡上的影长 CD 为 4 米，ABBC，同一时刻，光线与旗杆的夹角为 37，斜坡的坡角为 30，旗杆的高度 AB 约为（ ）米（参考数据：sin370.6，cos370.8，tan370.75， 1.73）3A. 10.61 B. 10.52 C. 9.87 D. 9.37二、填空题（共 10
4、题；共 30 分）11.如图所示，在建筑物 AB 的底部 a 米远的 C 处，测得建筑物的顶端 A 点的仰角为 ，则建筑物 AB 的高可表示为_12.如图，在边长为 1 的小正反形组成的网格中，ABC 的三个顶点均在格点上，则 tanB 的值为_ 13.如图，从甲楼底部 A 处测得乙楼顶部 C 处的仰角是 30，从甲楼顶部 B 处测得乙楼底部 D 处的俯角是45，已知甲楼的高 AB 是 120m，则乙楼的高 CD 是_m（结果保留根号）14.如图，在菱形 ABCD 中，AE BC，E 为垂足，若 cosB= ， EC=2，P 是 AB 边上的一个动点，则线段 PE45的长度的最小值是_ 15.
5、如图，ABC 中，C90，AC3，AB5 ，点 D 是边 BC 上一点若沿 AD 将 ACD 翻折，点 C 刚好落在 AB 边上点 E 处，则 BD_ 16.如下图，在矩形 ABCD 中，BC=6，CD=3，将 BCD 沿对角线 BD 翻折，点 C 落在点 C处，BC 交 AD 于点E，则线段 DE 的长为 _ 17.如图，某城市的电视塔 AB 坐落在湖边，数学老师带领学生隔湖测量电视塔 AB 的高度，在点 M 处测得塔尖点 A 的仰角AMB 为 22.5，沿射线 MB 方向前进 200 米到达湖边点 N 处，测得塔尖点 A 在湖中的倒影 A的俯角 ANB 为 45，则电视塔 AB 的高度为_
6、米（结果保留根号）18.在 RtABC 中， ACB=90， a=2，b=3 ，则 tanA=_ 19.如图，在等边ABC 中，AB=10，BD=4，BE=2，点 P 从点 E 出发沿 EA 方向运动，连结 PD，以 PD 为边，在 PD 的右侧按如图所示的方式作等边 DPF，当点 P 从点 E 运动到点 A 时，点 F 运动的路径长是_20.如图一-艘渔船正以 60 海里/小时的速度向正东方向航行,在 处测得岛礁 在东北方向上，继续航A P行 15 小时后到达 处此时测得岛礁 在北偏东 方向,同时测得岛礁 正东方向上的避风港 B P 30 P M在北偏东 方向为了在台风到来之前用最短时间到达
7、 处,渔船立刻加速以 75 海里/小时的速度继续60 M航行_小时即可到达 (结果保留根号)三、解答题（共 8 题；共 60 分）21.如图，锐角ABC 中，AB=10cm，BC=9cm，ABC 的面积为 27cm2 求 tanB 的值22.如图为护城河改造前后河床的横断面示意图，将河床原竖直迎水面 BC 改建为坡度 1：05 的迎水坡AB，已知 AB=4 米，则河床面的宽减少了多少米(即求 AC 的长)523.中考英语听力测试期间 T 需要杜绝考点周围的噪音如图，点 A 是某市一中考考点，在位于考点南偏西 15方向距离 500 米的 C 点处有一消防队在听力考试期间，消防队突然接到报警电话，
8、消防车需沿北偏东 75方向的公路 CF 前往救援已知消防车的警报声传播半径为 400 米，若消防车的警报声对听力测试造成影响，则消防车必须改道行驶试问：消防车是否需要改道行驶？说明理由（ 1.732）324.热气球的探测器显示，从热气球底部 A 处看一栋高楼顶部 B 的仰角为 30，看这栋楼底部 C 的俯角为45，已知楼高是 120m，热气球若要飞越高楼，问至少要继续上升多少米？（结果保留根号）25.如图:我渔政 310 船在南海海面上沿正东方向匀速航行,在 A 点观测到我渔船 C 在北偏东 60方向的我国某传统渔场捕鱼作业.若渔政 310 船航向不变,航行半小时后到达 B 点,观测到我渔船
9、C 在东北方向上.问: 渔政 310 船再按原航向航行多长时间, 离渔船 C 的距离最近?(渔船 C 捕鱼时移动距离忽略不计,结果不取近似值)26.如图，某煤矿因不按规定操作发生瓦斯爆炸，救援队立即赶赴现场进行救援，救援队利用生命探测仪在地面 A，B 两个探测点探测到地下 C 处有生命迹象已知 A，B 两点相距 8 米，探测线与地面的夹角分别是 30和 45，试确定生命所在点 C 的深度（结果保留根号）27.如图所示，一条自西向东的观光大道 l 上有 A、B 两个景点，A、B 相距 2km，在 A 处测得另一景点 C位于点 A 的北偏东 60方向，在 B 处测得景点 C 位于景点 B 的北偏东
10、 45方向，求景点 C 到观光大道 l 的距离（结果精确到 0.1km）28.如图，图是某电脑液晶显示器的侧面图，显示屏 AO 可以绕点 O 旋转一定的角度研究表明：显示屏顶端 A 与底座 B 的连线 AB 与水平线 BC 垂直时（如图），人观看屏幕最舒适此时测得BAO 15，AO30cm，OBC 45 ，求 AB 的长度（结果精确到 1 cm）（参考数据：sin150.26，cos150.97 ， tan150.27， 1.414）2答案解析部分一、单选题1.【答案】B 【考点】特殊角的三角函数值 【解析】【解答】解：sin60= 32故答案为：B【分析】由特殊角的三角函数值可求解。2.【答
11、案】A 【考点】特殊角的三角函数值 【解析】【分析】根据特殊角的三角函数值，结合选项进行判断cos30= ，32B=30故选 A3.【答案】B 【考点】勾股定理，锐角三角函数的定义 【解析】【解答】解：在 RtABC 中，由勾股定理得，BC= =12，AB2-AC2sinA= = ，BCAB1213故答案为：B【分析】在 RtABC 中，由勾股定理求出 BC 的长，再根据锐角三角函数的意义可求 sinA 的值。4.【答案】B 【考点】特殊角的三角函数值 【解析】【分析】根据已知条件先判断出三角形的形状，再根据特殊角的三角函数值求解即可C=90，AC=BC ，该三角形为等腰直角三角形，sinA=
12、sin45= 22故选 B5.【答案】A 【考点】解直角三角形 【解析】【分析】根据 sinB 等于B 的对边与斜边之比可得 AB 的值【解答】sin B ，AC=9，35 = ，ACAB35解得 AB=15故选 A【点评】考查锐角三角函数的定义；用到的知识点为：一个角的正弦值，等于这个角的对边与斜边之比6.【答案】B 【考点】解直角三角形的应用坡度坡角问题 【解析】【解答】解：坡度为 1：7 ，设坡角是 ，则 sin= ， 112+72= 152= 210上升的高度是：30 =3 米210 2故选 B【分析】根据坡度即可求得坡角的正弦值，根据三角函数即可求解7.【答案】D 【考点】计算器三角
13、函数 【解析】【解答】解：由 tanB= ，得ACBCAC=BCtanB=5tan26故答案为：D【分析】根据三角函数的定义 tanB=AC：BC，得到 AC=BCtanB，得到正确的按键顺序.8.【答案】C 【考点】特殊角的三角函数值 【解析】【解答】解：由题意得，sinA =0， cosB=0，12 22即 sinA= ， =cosB，12 22解得，A=30，B=45，C=180AB=105，故选：C【分析】根据非负数的性质列出关系式，根据特殊角的三角函数值求出A 、B 的度数，根据三角形内角和定理计算即可9.【答案】D 【考点】勾股定理，锐角三角函数的定义 【解析】【分析】根据勾股定理
14、求出 c 的长，再根据锐角三角函数的概念求出A 的余弦值即可在 ABC 中，C=90， , ，a=5b=12c= ，52+122=13cosA= bc=1213故选 D10.【 答案】A 【考点】解直角三角形，解直角三角形的应用 【解析】【解答】解：如图，过点 C 作 CGEF 于点 G，延长 GH 交 AD 于点 H，过点 H 作 HPAB 于点 P，则四边形 BCHP 为矩形，BC=PH=6，BP=CH， CHD=A=37，AP= = =8，PHtan A 60.75过点 D 作 DQGH 于点 Q，CDQ=CEG=30，CQ= CD=2，DQ=CDcos CDQ=4 =2 ，12 32
15、3QH= = = ，DQtan CHD230.75833CH=QHCQ= 2，833则 AB=AP+PB=AP+CH=8+ 210.61，833故答案为：A【分析】通过作垂线把特殊角放在直角三角形中，利用三角函数由边求边，即由 PH 求 AP，由 DQ 可求出QH，最后 AP+PB=AB 求出旗杆高度.二、填空题11.【 答案】atan 【考点】锐角三角函数的定义 【解析】【解答】在直角ABC 中，B=90，C= ，BC=a ，tanC= ，ABBCAB=BCtanC=atan故答案为：atan【分析】根据正切函数的定义进行变形可得结果.12.【 答案】 34【考点】锐角三角函数的定义 【解析
16、】【解答】解：如图： ，tanB= = ADBD34故答案是： 34【分析】根据在直角三角形中，正切为对边比邻边，可得答案13.【 答案】 403【考点】解直角三角形的应用仰角俯角问题 【解析】【解答】由题意可得：BDA=45 ，则 AB=AD=120m，又CAD=30，在 RtADC 中，tanCDA=tan30= ，CDAD= 33解得：CD=40 （m），3故答案为：40 3【分析】在 RtABD 中，可得 AD=AB=120m；在 RtADC 中，由 tanCDA=tan30= 可求得 CD。CDAD14.【 答案】4.8 【考点】解直角三角形 【解析】【解答】解：设菱形 ABCD 的
17、边长为 x，则 AB=BC=x，又 EC=2，所以 BE=x2，因为 AEBC 于 E，所以在 RtABE 中，cosB= ， 又 cosB= ， x-2x 45于是 = ， x-2x 45解得 x=10，即 AB=10所以易求 BE=8，AE=6，当 EPAB 时，PE 取得最小值故由三角形面积公式有： ABPE= BEAE，12 12求得 PE 的最小值为 4.8故答案为 4.8【分析】设菱形 ABCD 的边长为 x，则 AB=BC=x，又 EC=2，所以 BE=x2，解直角 ABE 即可求得 x 的值，即可求得 BE、AE 的值，根据 AB、PE 的值和 ABE 的面积，即可求得 PE
18、的最小值15.【 答案】2.5 【考点】勾股定理，轴对称的性质 【解析】【解答】AC 3，AB5 ，BC= =4，AB2-AC2设 BD=x，则 CD=4x，ED=4x，AE=AC=3，BE=2，BE2+DE2=BD2 ， 22+（4x） 2=x2 ， 解得 x=2.5，BD=2.5.故答案为：2.5.【分析】在 RtABC 中应用勾股定理可求得 BC=4，设 BD=x，则结合轴对称的两个三角形全等可用 x 表示出 ED=4x，在 RtBED 中应用勾股定理即可得到关于 x 的方程，解方程即可求得 x 即 BD 的长.16.【 答案】3.75 【考点】翻折变换（折叠问题） 【解析】【解答】解：
19、设 ED=x，则 AE=6x， 四边形 ABCD 为矩形，ADBC，EDB=DBC；由题意得：EBD= DBC，EDB=EBD，EB=ED=x；由勾股定理得：BE2=AB2+AE2 ， 即 x2=9+（6 x） 2 ， 解得：x=3.75 ，ED=3.75故答案为：3.75【分析】首先根据题意得到 BE=DE，然后根据勾股定理得到关于线段 AB、AE 、BE 的方程，解方程即可解决问题17.【 答案】100 2【考点】解直角三角形的应用仰角俯角问题 【解析】【解答】解：如图，连接 AN，由题意知，BMAA，BA=BAAN=AN，ANB=ANB=45，AMB=22.5，MAN=ANBAMB=22
20、.5=AMN，AN=MN=200 米，在 RtABN 中，ANB=45 ，AB= AN=100 （米），22 2故答案为 100 2【分析】根据垂直平分线的性质，线段垂直平分线上的点与线段的两个端点的距离相等，得到 AN=AN，再根据勾股定理求出 AB 的值.18.【 答案】 23【考点】锐角三角函数的定义 【解析】【解答】解：在 RtABC 中，ACB=90，a=2 ，b=3，tanA= = ab23故答案为 23【分析】根据三角函数可得 tanA= ， 再把 a=2，b=3 代入计算即可ab19.【 答案】8 【考点】全等三角形的判定与性质，等边三角形的判定与性质，解直角三角形 【解析】【
21、解答】解：如图，ABC 为等边三角形，B=60，过 D 点作 DEAB，则 BE= BD=2，12点 E与点 E 重合，BDE=30，DE= BE=2 ，3 3DPF 为等边三角形，PDF=60，DP=DF，EDP+HDF=90HDF+DFH=90，EDP=DFH，在DPE 和FDH 中， PED= DHF EDP= DFHDP=FDDPEFDH，FH=DE=2 ，3点 P 从点 E 运动到点 A 时，点 F 运动的路径为一条线段，此线段到 BC 的距离为 2 ，3当点 P 在 E 点时，作等边三角形 DEF1 ， BDF1=30+60=90，则 DF1BC，当点 P 在 A 点时，作等边三角
22、形 DAF2 ， 作 F2QBC 于 Q，则DF 2QADE，所以 DQ=AE=102=8，F1F2=DQ=8，当点 P 从点 E 运动到点 A 时，点 F 运动的路径长为 8【分析】过 F 点作 FHBC，过 D 点作 DEAB，点 E与点 E 重合，根据已知条件可以求出 DE 的长，接着证明DPE 和FDH ，得出 FH=DE，就可以判断点 F 的运动轨迹是一条线段，此线段到 BC 的距离为就是 FH的长，分别作出点 P 在 E、A 两点时的等边 DEF1， 等边 DAF2， 再去证明DQF 2ADE，得到 DQ=AE=F1F2 ， 即可求出点 F 的运动的路径长。20.【 答案】 18+
23、635【考点】解直角三角形的应用方向角问题 【解析】【解答】如图，过点 P 作 PQAB 交 AB 延长线于点 Q，过点 M 作 MNAB 交 AB 延长线于点 N，在直角AQP 中， PAQ=45，则 AQ=PQ=601.5+BQ=90+BQ（海里），所以 BQ=PQ-90在直角BPQ 中， BPQ=30，则 BQ=PQtan30= PQ（海里），33所以 PQ-90= PQ，33所以 PQ=45（3+ ）（海里）3所以 MN=PQ=45（3+ ）（海里）3在直角BMN 中， MBN=30，所以 BM=2MN=90（3+ ）（海里）3所以 （小时）90(3+3）75 =18+635故答案是：
24、 18+635【分析】根据题意，添加辅助线：过点 P 作 PQAB 交 AB 延长线于点 Q，过点 M 作 MNAB 交 AB 延长线于点 N，在 RtAQP 和 RtBPQ 中，利用解直角三角形分别求出 BQ=PQ-90，及 BQ= PQ，建立方程求33出 PQ 及 MN 的长，从而可求出 MB 的长，再根据路程除以速度 =时间，即可求解。三、解答题21.【 答案】解：过点 A 作 AHBC 于 H，SABC=27， ，129AH=27AH=6，AB=10，BH= = =8，AB2-AH2 102-62tanB= = = AHBH68 34【考点】三角形的面积，勾股定理，锐角三角函数的定义
25、【解析】【分析】 过点 A 作 AHBC 于 H，根据ABC 的面积为 27 可求出 AH 的长，在直角三角形 ABH中用勾股定理求出 BH 的长，则 tanB 的值可求。22.【 答案】解：设 AC 的长为 x，那么 BC 的长就为 2xx2+（2x） 2=AB2 ， x2+（2x） 2=（4 ） 2 ， 5x=4答：河床面的宽减少了 4 米 【考点】解直角三角形的应用坡度坡角问题 【解析】【分析】因为坡度为 1：0.5 ，可知道 = ， 设 AC 的长为 x，那么 BC 的长就为 2x，根据勾股定理可列出方程求解23.【 答案】解：过 A 作 ADCF 于 D，由题意得CAG=15，ACE
26、=15，ECF=75，ACD=60 ，在 RtACD 中，sinACD= ，ADAC则 AD=ACsinACD=250 433 米，433 米400 米，不需要改道3答：消防车不需要改道行驶 【考点】解直角三角形的应用方向角问题 【解析】【分析】方向角问题需要首先构造直角三角形，所以过 A 作 ADCF 于 D，易得ACD=60利用三角函数易得 AD=433400,所以可得结果。24.【 答案】解:设 BD=x 米，则 CD=（120-x）米因为DAC=45所以 AD=CD=（120-x ）米BAD=30答：热气球若要飞越高楼，至少要继续上升 BDAD=tan30，即 x120-x= 33，解
27、得 x=(603-60)m(603-60)m【考点】特殊角的三角函数值，解直角三角形，解直角三角形的应用仰角俯角问题 【解析】【分析】将实际问题转化为数学问题，可知DAC=45 ， BAD=30，BC=120，因此设 BD=x 米，则 CD=（ 120-x）米，在 RtADC 中，可表示出 AD 的长，再在 RtABD 中，利用解直角三角形,建立关于 x的方程，求解即可。25.【 答案】解:作 CDAB,交 AB 的延长线于 D,则当渔政 310 船航行到 D 处时,离渔船 C 的距离最近.设 CD长为 x,在 RtACD 中,AD=CD tan 60= x,在 RtBCD 中,BD=CD=x
28、, AB=AD-BD= x-x=( -1)x,设渔政船从3 3 3B 航行到 D 需要 t 小时, 则 t=BD=x,解得 t= = .(3-1)x0.5 12(3-1) 3+14答: 渔政 310 船再按原航向航行 小时后, 离渔船 C 的距离最近 3+14【考点】解直角三角形的应用方向角问题 【解析】【分析】先找出渔政船 310 离渔船 C 的距离的位置：因为渔政船 310 的航线是在直线 AB 上，点C 到直线 AB 上的垂线段最短，所以作 CDAB,交 AB 的延长线于 D,CD=x，再用 x 表示出 AB 的长，根据行程关系列方程即可解出。26.【 答案】解：作 CDAB 交 AB
29、的延长线于点 D，如右图所示， 由已知可得，AB=8 米， CBD=45，CAD=30，AD= ， BD= ，CDtan30 CDtan45AB=ADAB= ，CDtan30- CDtan45即 8= ，CD33-CD1解得，CD= 米，(43+4)即生命所在点 C 的深度是 米 (43+4)【考点】解直角三角形的应用 【解析】【分析】根据题意作出合适的辅助线，然后根据特殊角的三角函数值，即可求得生命所在点 C的深度.27.【 答案】解：如图，过点 C 作 CDl 于点 D，设 CD=xkm，在ACD 中，ADC=90 ，CAD=30，AD= CD= xkm。3 3在BCD 中， BDC=90
30、，CBD=45 ，BD=CD=xkm。ADBD=AB， xx=2，x= +12.7（km）。3 3答：景点 C 到观光大道 l 的距离约为 2.7km【考点】解直角三角形的应用方向角问题 【解析】【分析】如图，过点 C 作 CDl 于点 D，设 CD=xkm，在ACD 中，根据含 30角的直角三角形的边之间的关系表示出 AD，在 BCD 中，利用等腰直角三角形的性质得出 BD=CD=xkm。根据 ADBD=AB 建立方程，求解得出 x 的值。28.【 答案】解：过 O 点作 ODAB 交 AB 于 D 点在 RtADO 中，A=15，AO=30，OD=AOsin15300.26=7.8（cm） AD=AOcos15300.97=29.1（cm）又 在 RtBDO 中，OBC=45，BD=OD=7.8（cm ），AB=AD+BD36.9（cm ）答：AB 的长度为 36.9cm 【考点】解直角三角形 【解析】【分析】根据角的度数，以及提供的数据构造直角三角形过 O 点作 ODAB 交 AB 于 D 点，则AB=AD+BD=AD+OD，即要求出 AD 和 OD，在 RtBDO 中，A=15，AO=30，可求得 AD 和 OD.
