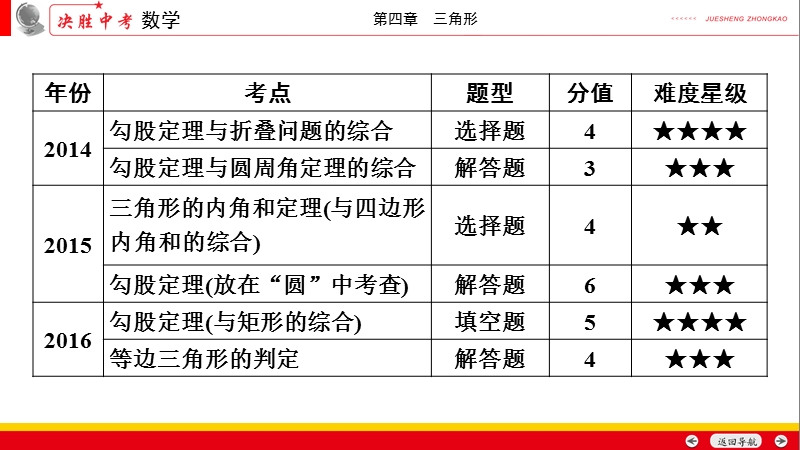
1、安徽中考20142018 考情分析,基础知识梳理,中考真题汇编,安徽中考20142018 考情分析,说明：从上表可以看出安徽中考对本节内容的考查，“勾股定理”是必考知识，“等腰三角形、三角形的中位线”等属于安徽中考的核心考点，考查难度一般要看与其他知识的综合程度，在“一般”与“较难”之间，分值在10分左右 预测2019年安徽中考命题趋势：(1)以三角形边、角关系为考查点的试题；(2)以“勾股定理”为主题的数学文化类试题；(3)将“等腰三角形”融入到函数中考查，体现“数形结合”与“分类讨论”,基础知识梳理,不等边三角形,等边三角形,直角三角形,2三角形的三边关系：三角形的任意两边之和_第三边；三
2、角形的任意两边之差_第三边 3三角形的内角和定理及其外角性质 (1)三角形的内角和等于_； (2)三角形的外角性质：三角形的任意一个外角等于和它不相邻的_的和；三角形的外角大于和它不相邻的_.,大于,小于,180,两个内角,任意一个内角,考点二 三角形中的重要线段,90,BAC,BC,4.三角形的中位线：连接三角形两边_的线段，叫做三角形的中位线； 三角形中位线的性质定理：三角形的中位线平行于_，且等于第三边的_.,中点,第三边,一半,相等,相等,中线和高,相等,4等边三角形 (1)等边三角形的性质：等边三角形的三条边_；等边三角形的三个角都是_. (2)等边三角形的判定：a.三边_的三角形是
3、等边三角形；b.三个角_的三角形是等边三角形；c.有两个角是_的三角形是等边三角形；d.有一个角是_的等腰三角形是等边三角形,相等,60,相等,都相等,60,60,考点四 直角三角形 1直角三角形的性质： (1)直角三角形的两个锐角_； (2)直角三角形的斜边上的中线等于斜边的_； (3)直角三角形中，30的角所对的直角边等于斜边的_；等于斜边的一半的直角边所对的角是_； (4)勾股定理：直角三角形的两条直角边的平方和等于斜边的_.,互余,一半,一半,30,平方,90,一半,平方和,考点五 三角形的稳定性 当三角形的三边一定时，三角形的形状和大小就_，而不能再发生改变，这就是三角形的稳定性；三
4、角形的稳定性的根据就是判定三角形全等的_定理,一定,边边边,一、三角形的边角关系 【例1】 ABC中，AB5，AC3，AD是ABC的中线，设AD长为m，则m的取值范围是_,【解析】 延长AD至点E，使DEAD，连接EC，BDCD，DEAD，ADBEDC，ABDECD，CEAB，AB5，AC3，CE5，设ADm，则AE2m，532m53，1m4. 【答案】 1m4 【点拨】 倍长中线是解答此类问题的常用方法，应用三角形的三边关系是解答本题的突破口,【例2】 (2018聊城)如图，将一张三角形纸片ABC的一角折叠，使点A落在ABC外的A处，折痕为DE.如果A，CEA，BDA，那么下列式子中正确的是
5、 ( ) A2 B2 C D180,【解析】 设AD交AC于点F.由折叠可知，AA.由三角形的外角定理，得AFDCEAA，BDAAAFD，即2. 【答案】 A 【点拨】 本题解答过程中充分运用了转化思想，即把要探求的角转化到同一个三角形中，而转化的依据往往是三角形内角和或三角形外角的性质,二、三角形中的主要线段 【例3】 (2018襄阳)已知CD是ABC的边AB上的高，若CD，AD1，AB2AC，则BC的长为_,【点拨】 遇到三角形的高的问题，若没有给定三角形，一般需要分锐角三角形和钝角三角形进行讨论如本题分两种情况，分别在两个图形中利用勾股定理求出BD和CD，从而求出BC的长,三、等腰三角形
6、 【例4】 如图，AD平分BAC，ADBD，垂足为点D，DEAC求证：BDE是等腰三角形,【解析】 如图，直接利用平行线的性质得出13，进而利用角平分线的定义结合互余的性质得出BBDE，即可得出答案,【答案】 证明：DEAC，13.AD平分BAC，12.23.又ADBD，2B90，3BDE90.BBDE.EBED，即BDE是等腰三角形 【点拨】 角的平分线、平行线、等腰三角形，这三者当中具备其二，第三者必定成立,【答案】 C,【点拨】 根据三角形的三边数量关系，可以判断一个三角形是否是直角三角形，这一点在解题中需引起重视另外，直角三角形有很多的性质，如30角的性质，斜边上的中线等于斜边的一半以
7、及勾股定理等，这些性质在研究有关等边三角形、等腰三角形、直角三角形的问题时，会为我们证明或解决问题创造条件,1一个等腰三角形的两条边长分别是方程x27x100的两根，则该等腰三角形的周长是 ( ) A12 B9 C13 D12或9,A,2如图，ABC中，AD是BC边上的高，AE，BF分别是BAC，ABC的平分线，BAC50，ABC60，则EADACD ( ) A75 B80 C85 D90,A,3(2017泰州)三角形的重心是 ( ) A三角形三条边上中线的交点 B三角形三条边上高线的交点 C三角形三条边垂直平分线的交点 D三角形三条内角平行线的交点,A,4已知如图，四边形ABCD中，ABBC
8、，AC，求证：ADCD证明：连接ACABAC，BACBCA，又AC，即BACDACBCADCA，DACDCA，ADCD,中考真题汇编,1(2018安徽)如图1，RtABC中，ACB90，点D为边AC上一点，DEAB于点E，点M为BD中点，CM的延长线交AB于点F.,(1)求证：CMEM； (2)若BAC50，求EMF的大小； (3)如图2，若DAECEM，点N为CM的中点，求证：ANEM.,D,C,4(2018长沙)下列长度的三条线段，能组成三角形的是 ( ) A4 cm,5 cm,9 cm B8 cm,8 cm,15 cm C5 cm,5 cm,10 cm D6 cm,7 cm,14 cm,
9、5(2018福建)如图，等边三角形ABC中，ADBC，垂足为D，点E在线段AD上，EBC45，则ACE等于 ( ) A15 B30 C45 D60,A,B,C,8(2018扬州)在RtABC中，ACB90，CDAB于D，CE平分ACD交AB于E，则下列结论一定成立的是 ( ) ABCEC BECBE CBCBE DAEEC,C,90或130,11(2018宜昌)如图，在RtABC中，ACB90，A40，ABC的外角CBD的平分线BE交AC的延长线于点E.(1)求CBE的度数； (2)过点D作DFBE，交AC的延长线于点F，求F的度数,12(2018嘉兴)已知：在ABC中，ABAC，D为AC的中点，DEAB，DFBC，垂足分别为点E，F，且DEDF.求证：ABC是等边三角形,13(2018长沙，节选)如图，在ABC中，AD是边BC上的中线，BADCAD，CEAD，CE交BA的延长线于点E，BC8，AD3.(1)求CE的长； (2)求证：ABC为等腰三角形,
