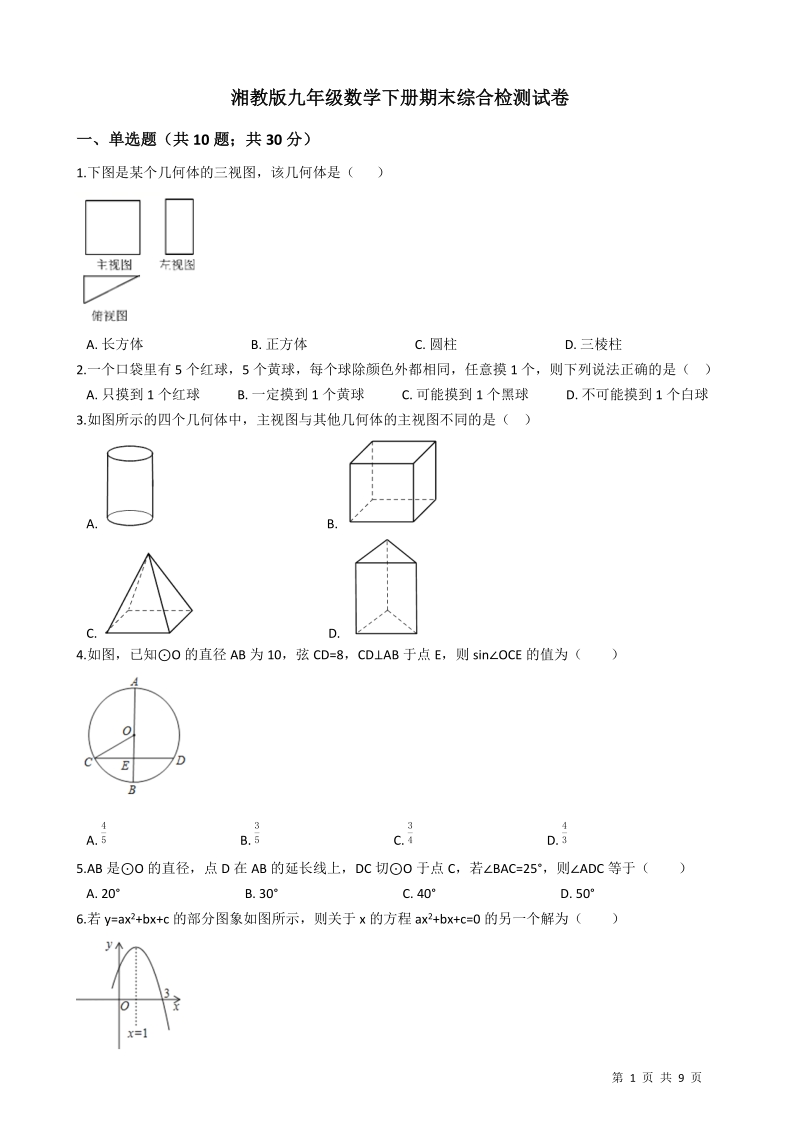
1、 第 1 页 共 9 页湘教版九年级数学下册期末综合检测试卷一、单选题（共 10 题；共 30 分）1.下图是某个几何体的三视图，该几何体是（ ）A. 长方体 B. 正方体 C. 圆柱 D. 三棱柱2.一个口袋里有 5 个红球，5 个黄球，每个球除颜色外都相同，任意摸 1 个，则下列说法正确的是（ ） A. 只摸到 1 个红球 B. 一定摸到 1 个黄球 C. 可能摸到 1 个黑球 D. 不可能摸到 1 个白球3.如图所示的四个几何体中，主视图与其他几何体的主视图不同的是（ ） A. B. C. D. 4.如图，已知O 的直径 AB 为 10，弦 CD=8，CD AB 于点 E，则 sinOC
2、E 的值为（ ）A. B. C. D. 45 35 34 435.AB 是 O 的直径，点 D 在 AB 的延长线上，DC 切 O 于点 C，若BAC=25 ，则ADC 等于（ ） A. 20 B. 30 C. 40 D. 506.若 y=ax2+bx+c 的部分图象如图所示，则关于 x 的方程 ax2+bx+c=0 的另一个解为（ ）第 2 页 共 9 页A. -2 B. -1 C. 0 D. 17.如图，在平行四边形 ABCD 中，BD AD，以 BD 为直径作圆，交于 AB 于 E，交 CD 于 F，若BD=12，AD：AB=1：2，则图中阴影部分的面积为（ ）A. 12 B. C. D
3、. 3 153-6 303-12 483-368.将抛物线 y=2x2 向左平移 1 个单位，再向上平移 3 个单位得到的抛物线，其表达式为（ ） A. y=2（x1） 23 B. y=2（x1） 23 C. y=2（x1 ） 23 D. y=2（x 1 ） 239.一个点到圆的最大距离为 9cm，最小距离为 4cm，则圆的半径是（ ） A. 5cm 或 13cm B. 2.5cm C. 6.5cm D. 2.5cm 或 6.5cm10.如图二次函数 的图象与 轴交于（ 1，0），（3，0）；下列说法正确的是（ ）y=ax2+bx+c xA. B. 当 时，y 随 x 值的增大而增大 C. D
4、. 当 时，abc1 a+b+c0 y0-1x3二、填空题（共 10 题；共 39 分）11.正八边形的中心角等于_度. 12.“明天的太阳从西方升起”这个事件属于_事件（用“必然” 、“不可能” 、“不确定”填空） 13.将抛物线 y=x2-2 向上平移一个单位后，得一新的抛物线，那么新的抛物线的表达式是_ 14.我们把两个三角形的外心之间的距离叫做外心距如图，在 RtABC 和 RtACD 中， ACB=ACD=90，点 D 在边 BC 的延长线上，如果 BC=DC=3，那么 ABC 和ACD 的外心距是 _15.抛物线 y=x22x+3 用配方法化成 y=a（x h） 2+k 的形式是_
5、，抛物线与 x 轴的交点坐标是_，抛物线与 y 轴的交点坐标是 _ 16.抛物线 与 轴只有一个公共点，则 的值为_ y=2x2+8x+m x m17.在 O 中，弦 AB=2cm，圆心角 AOB=60，则O 的直径为 _ cm 第 3 页 共 9 页18.如图，AB 为O 直径，E 是 BC 中点，OE 交 BC 于点 D，BD=3，AB=10，则 AC=_19.若扇形的半径为 3cm，扇形的面积为 2cm2 ， 则该扇形的圆心角为_ ，弧长为_ cm 20.如图，PA、PB 分别切圆 O 于 A、B 两点，并与圆 O 的切线分别相交于 C、D 两点， 已知 PA=7cm，则PCD 的周长等
6、于_ 三、解答题（共 8 题；共 64 分）21.某鞋店有 A、B、C、D 四款运动鞋，元旦期间搞“买一送一 ”促销活动，用树状图或表格求随机选取两款不同的运动鞋，恰好选中 A、C 两款的概率 22.已知如图，在以 O 为圆心的两个同心圆中，大圆的弦 AB 交小圆于 C，D 两点。试说明： AC=BD。23.如图，用 50m 长的护栏全部用于建造一块靠墙的长方形花园，写出长方形花园的面积 y（m 2）与它与墙平行的边的长 x（m）之间的函数 第 4 页 共 9 页24.如图，AB 是O 的直径，点 F、C 在O 上且 ， 连接 AC、AF，过点 C 作 CDAF 交 AF 的BC= CF延长线
7、于点 D（1 ）求证：CD 是 O 的切线；（2 ）若 ， CD=4，求 O 的半径AF= FC25.给定关于 的二次函数 ，x y=2x2+(6-2m)x+3-m学生甲：当 时，抛物线与 轴只有一个交点，因此当抛物线与 轴只有一个交点时， 的值m=3 x x m为 3；学生乙：如果抛物线在 轴上方，那么该抛物线的最低点一定在第二象限；x请判断学生甲、乙的观点是否正确，并说明你的理由. 26. 如图，在ABC 中， C=90，AB=5，BC=4 ，以 A 为圆心，3 为半径作圆.试判断：点 C 与A 的位置关系；点 B 与A 的位置关系；AB 中的 D 点与A 的位置关系.第 5 页 共 9
8、页27.已知：二次函数 y=ax 2+bx+c（a0）的图象如图所示请你根据图象提供的信息，求出这条抛物线的表达式 28.如图，AB 是O 的直径，过点 B 作O 的切线 BM，弦 CDBM，交 AB 于点 F，且 = ， 连接AC，AD，延长 AD 交 BM 于点 E（1 ）求证：ACD 是等边三角形；（2 ）连接 OE，若 DE=2，求 OE 的长第 6 页 共 9 页答案解析部分一、单选题1.【答案】D 2.【答案】D 3.【答案】C 4.【答案】B 5.【答案】C 6.【答案】B 7.【答案】C 8.【答案】A 9.【答案】D 10.【 答案】B 二、填空题11.【 答案】45 12.
9、【 答案】不可能 13.【 答案】y=x 2-1 14.【 答案】3 15.【 答案】y=（x+1） 2+4；（ 1，0），（3 ，0）；（0 ，3） 16.【 答案】8 17.【 答案】4 18.【 答案】8 19.【 答案】80 ； 4320.【 答案】14 三、解答题21.【 答案】解：画树状图得：共有 12 种等可能的结果，恰好选中 A、C 两款的有 2 种情况，恰好选中 A、C 两款的概率为： = 21216第 7 页 共 9 页22.【 答案】解：过 点作 于 O OE AB E根据垂径定理则有 AE=BE,CE=DE所以 AE-CE=BE-DE即： AC=BD23.【 答案】解：
10、 与墙平行的边的长为 x（m），则垂直于墙的边长为： =（25 0.5x）m， 根据题意得出：y=x（25 0.5x）=0.5x 2+25x 24.【 答案】（1）证明：连结 OC，如图， ，BC= CFFAC=BAC，OA=OC，OAC=OCA，FAC=OCA，OCAF，CDAF，OCCD，CD 是O 的切线；（2 ）解：连结 BC，如图，AB 为直径，ACB=90， = ，BC= CFAFBOC= 180=60，13BAC=30，DAC=30，在 RtADC 中，CD=4，AC=2CD=8，在 RtACB 中， BC2+AC2=AB2 ， 即 82+（ AB） 2=AB2 ， 12AB=
11、，1633第 8 页 共 9 页O 的半径为 83325.【 答案】解：甲的观点是错误的.理由如下：当抛物线 与 轴只有一个交点时y=2x2+(6-2m)x+3-m x(6-2m)2-42(3-m)=0即： (3-m)(4-4m)=0解得 或 m=3 m=1即 或 时抛物线 与 轴只有一个交点m=3 m=1 y=2x2+(6-2m)x+3-m x乙的观点是正确的理由如下：当抛物线在 轴上方时，x由上可得 (6-2m)2-42(3-m)0即： (3-m)(4-4m)0 1m3而对于开口向上的抛物线最低点为其顶点顶点的横坐标为 x= -6-2m22=m-32，且抛物线在 轴上方， 1m3 x=m-
12、32 0 x即抛物线的最低点在第二象限 26.【 答案】解：C=90，AB=5，BC=4，AC=3，BA=5，DA=2.5，AC=r=3，点 C 在 A 上； BA=53 ，BAr ， 点 B 在 A 外； DA=2.53，DA r ， 点 D 在A 外内. 27.【 答案】解：由图象可知：抛物线的对称轴为 x=1， 设抛物线的表达式为：y=a（x1 ） 2+k抛物线经过点（ 1，0）和（0， 3） 解得 ，抛物线的表达式为：y=（x 1） 24，即 y=x22x3 28.【 答案】（1）证明： AB 是O 的直径，BM 是O 的切线，ABBE，第 9 页 共 9 页CDBE，CDAB， ， = ， ， AD=AC=CD，ACD 是等边三角形；（2 ）解：连接 OE，过 O 作 ONAD 于 N，由（1 ）知， ACD 是等边三角形，DAC=60AD=AC，CDAB，DAB=30，BE= AE，ON= AO，12 12设 O 的半径为：r ，ON= r，AN=DN= r，12 32EN=2+ r，BE= AE= ，32 12 3r+22在 RtNEO 与 RtBEO 中，OE2=ON2+NE2=OB2+BE2 ， 即（ ） 2+（2+ ） 2=r2+ ，r2 3r2 (3r+22 )2r= ，23OE2= +25=28，( 3)2OE= 27
