 【期末复习】人教版七年级数学上册《第三章一元一次方程》单元检测试卷含答案(PDF版)
【期末复习】人教版七年级数学上册《第三章一元一次方程》单元检测试卷含答案(PDF版)
《【期末复习】人教版七年级数学上册《第三章一元一次方程》单元检测试卷含答案(PDF版)》由会员分享,可在线阅读,更多相关《【期末复习】人教版七年级数学上册《第三章一元一次方程》单元检测试卷含答案(PDF版)(19页珍藏版)》请在七七文库上搜索。
1、人 教 版 七 年 级 初 中 数 学 上 册 : 第 三 章 一 元 一 次 方 程 单 元 检 测 试卷一 选 择 题 ( 共 10 小 题 )1 关 于 x 的 方 程 ( m2 1) x2+( m 1) x+7m2=0 是 一 元 一 次 方 程 , 则 m 的 取 值是 ( )A m=0 B m= 1 C m= 1 D m 12 有 一 “ 数 值 转 换 机 ” 如 图 所 示 , 则 输 出 的 结 果 为 ( )A x B C D3 在 有 理 数 范 围 内 定 义 运 算 “ *” , 其 规 则 为 a*b= , 则 方 程 ( 2*3) ( 4*x)=49 的 解 为
2、( )A 3 B 55 C 56 D 554 下 列 运 用 等 式 性 质 进 行 变 形 : 如 果 a=b, 那 么 a c=b c; 如 果 ac=bc,那 么 a=b; 由 2x+3=4, 得 2x=4 3; 由 7y= 8, 得 y= , 其 中 正 确 的有 ( )A 1 个 B 2 个 C 3 个 D 4 个5 已 知 关 于 x 的 方 程 2x a 5=0 的 解 是 x=b, 则 关 于 x 的 方 程 3x a+2b= 1的 解 为 ( )A x= 1 B x=1 C x=2 D x= 26 如 图 , 边 长 为 a 的 正 方 形 中 阴 影 部 分 的 面 积 为
3、 ( )A a2 a2 B a2 C a2 a2 D a27 在 国 道 107 工 程 施 工 现 场 , 调 来 72 名 司 机 师 傅 参 加 挖 土 和 运 土 工 作 , 已 知 3名 司 机 师 傅 挖 出 的 土 1 名 司 机 师 傅 恰 好 能 开 车 全 部 运 走 , 怎 样 分 配 这 72 名 司机 师 傅 才 能 使 挖 出 的 土 能 及 时 运 走 ? 解 决 此 问 题 , 可 设 : 派 x 名 司 机 师 傅 挖土 , 其 他 的 人 运 土 , 列 方 程 = ; 72 x= ; x+3x=72; =3上 述 所 列 方 程 , 正 确 的 有 ( )
4、 个 A 1 B 2 C 3 D 48 一 个 两 位 数 , 个 位 上 的 数 字 是 a, 十 位 上 的 数 字 比 个 位 的 数 字 小 1, 则 这 个 两位 数 可 以 表 示 为 ( )A a( a 1) B ( a+1) a C 10( a 1) +a D 10a+( a 1)9 深 圳 市 出 租 车 的 收 费 标 准 是 : 起 步 价 10 元 ( 行 驶 距 离 不 超 过 2km, 都 需 付10 元 车 费 ) , 超 过 2km 每 增 加 1km, 加 收 2.6 元 , 小 陈 乘 出 租 车 到 达 目 的 地 后共 支 付 车 费 49 元 , 那
5、么 小 陈 坐 车 可 行 驶 的 路 程 最 远 是 ( 不 考 虑 其 他 收 费 )( )A 15km B 16km C 17km D 18km10 在 梯 形 的 面 积 公 式 S= 中 , 已 知 S=48, h=12, b=6, 则 a 的 值 是( )A 8 B 6 C 4 D 2二 填 空 题 ( 共 7 小 题 )11 七 、 八 年 级 学 生 分 别 到 李 中 水 上 森 林 公 园 和 施 耐 庵 纪 念 馆 参 加 社 会 实 践 活 动 ,共 648 人 , 到 李 中 水 上 森 林 公 园 的 人 数 是 到 施 耐 庵 纪 念 纪 念 馆 人 数 的 2
6、倍 多48 人 设 到 施 耐 庵 纪 念 馆 的 人 数 为 x, 可 列 方 程 为 12 有 总 长 为 a 的 篱 笆 , 利 用 它 和 房 屋 的 一 面 墙 围 成 如 图 所 示 的 长 方 形 园 子 , 园子 的 宽 为 b, 则 所 围 成 的 园 子 的 面 积 为 13 一 个 两 位 数 , 个 位 上 的 数 字 为 a, 十 位 上 的 数 字 比 个 位 上 的 数 字 小 1, 若 将这 个 两 位 数 放 到 数 字 3 的 左 边 组 成 一 个 三 位 数 , 则 这 个 三 位 数 可 以 用 含 a 的代 数 式 表 示 ( 结 果 能 化 简 的
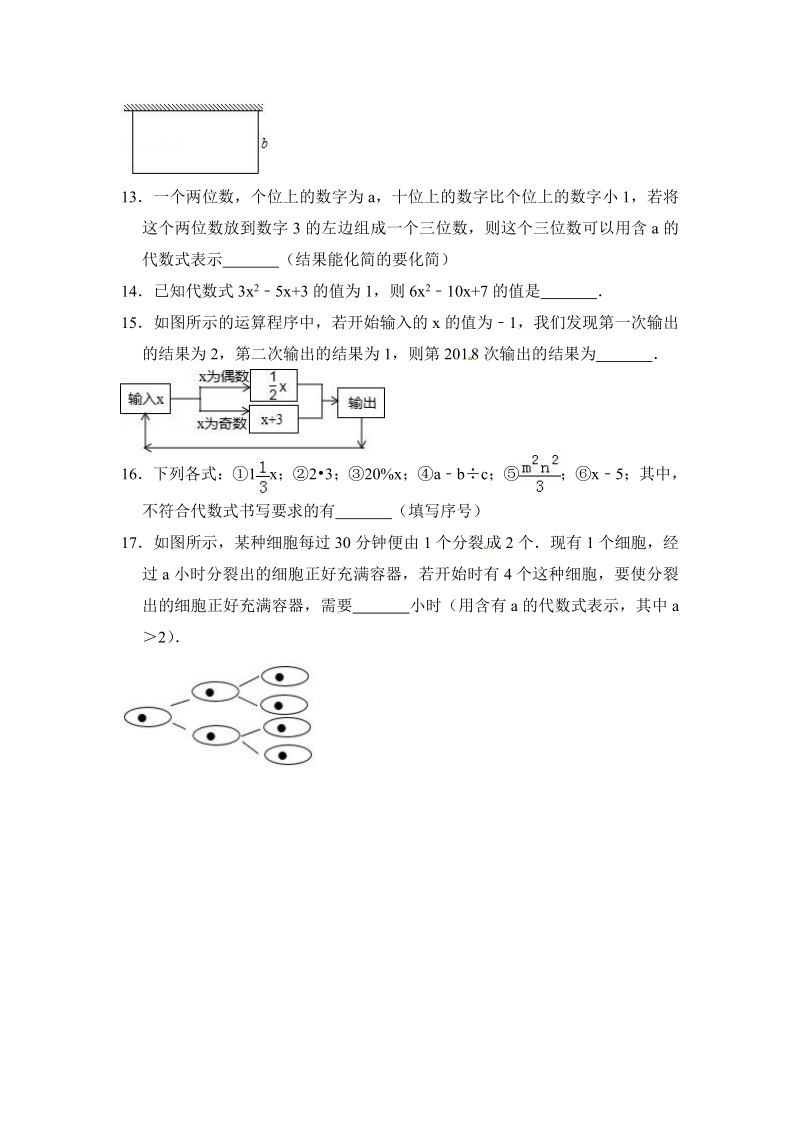
7、 要 化 简 )14 已 知 代 数 式 3x2 5x+3 的 值 为 1, 则 6x2 10x+7 的 值 是 15 如 图 所 示 的 运 算 程 序 中 , 若 开 始 输 入 的 x 的 值 为 1, 我 们 发 现 第 一 次 输 出的 结 果 为 2, 第 二 次 输 出 的 结 果 为 1, 则 第 2018 次 输 出 的 结 果 为 16 下 列 各 式 : 1 x; 23; 20%x; a b c; ; x 5; 其 中 ,不 符 合 代 数 式 书 写 要 求 的 有 ( 填 写 序 号 )17 如 图 所 示 , 某 种 细 胞 每 过 30 分 钟 便 由 1 个 分
8、 裂 成 2 个 现 有 1 个 细 胞 , 经过 a 小 时 分 裂 出 的 细 胞 正 好 充 满 容 器 , 若 开 始 时 有 4 个 这 种 细 胞 , 要 使 分 裂出 的 细 胞 正 好 充 满 容 器 , 需 要 小 时 ( 用 含 有 a 的 代 数 式 表 示 , 其 中 a 2) 三 解 答 题 ( 共 6 小 题 )18 解 方 程 :( 1) 2( x+3) =5x( 2) 1=3+19 如 图 , 这 是 一 个 数 值 转 换 机 的 示 意 图 ( 1) 若 输 入 x 的 值 为 2, 输 入 y 的 值 为 5, 求 输 出 的 结 果 ;( 2) 若 输
9、入 x 的 值 为 4, 输 出 的 结 果 为 8, 则 输 入 y 的 值 为 ( 直 接 填 空即 可 )20 如 图 , 两 个 大 小 正 方 形 的 边 长 分 别 是 4cm 和 xcm( 0 x 4) 并( 1) 用 含 x 的 式 子 表 示 图 中 阴 影 部 分 ( 三 角 形 ) 的 面 积 S, 并 化 简 ;( 2) 计 算 当 x=3 时 , 阴 影 部 分 的 面 积 21 当 m=2, n= 1 时 ,( 1) 求 代 数 式 ( m+n) 2和 m2+2mn+n2的 值 ;( 2) 观 察 下 面 图 形 面 积 的 不 同 表 示 法 , 直 接 写 出
10、( 1) 中 两 个 代 数 式 之 间 的 关 系 ;( 3) 请 用 简 便 的 方 法 计 算 出 当 m=0.125, n=0.875 时 , m2+2mn+n2的 值 22 如 图 , 点 O 为 原 点 , 已 知 数 轴 上 点 A 和 点 B 所 表 示 的 数 分 别 为 10 和 6,动 点 P 从 点 A 出 发 , 以 每 秒 6 个 单 位 长 度 的 速 度 沿 数 轴 正 方 向 匀 速 运 动 , 同时 动 点 Q 从 点 B 出 发 , 以 每 秒 3 个 单 位 的 速 度 沿 数 轴 负 方 向 匀 速 运 动 , 设 运动 时 间 为 t( t 0) 秒
11、( 1) 当 t=2 时 , 求 AP 的 中 点 C 所 对 应 的 数 ;( 2) 当 PQ=OA 时 , 求 点 Q 所 对 应 的 数 23 如 图 , 在 数 轴 上 点 A 表 示 的 有 理 数 为 6, 点 B 表 示 的 有 理 数 为 6, 点 P 从点 A 出 发 以 每 秒 4 个 单 位 长 度 的 速 度 在 数 轴 上 由 A 向 B 运 动 , 当 点 P 到 达 点B 后 立 即 返 回 , 仍 然 以 每 秒 4 个 单 位 长 度 的 速 度 运 动 至 点 A 停 止 运 动 , 设 运动 时 间 为 t( 单 位 : 秒 ) ( 1) 求 t=1 时
12、点 P 表 示 的 有 理 数 ;( 2) 求 点 P 与 点 B 重 合 时 的 t 值 ;( 3) 在 点 P 沿 数 轴 由 点 A 到 点 B 再 回 到 点 A 的 运 动 过 程 中 , 求 点 P 与 点 A 的距 离 ( 用 含 t 的 代 数 式 表 示 ) ;( 4) 当 点 P 表 示 的 有 理 数 与 原 点 的 距 离 是 2 个 单 位 长 度 时 , 请 求 出 所 有 满 足 条件 的 t 值 参 考 答 案一 选 择 题 ( 共 10 小 题 )1 关 于 x 的 方 程 ( m2 1) x2+( m 1) x+7m2=0 是 一 元 一 次 方 程 , 则
13、 m 的 取 值是 ( )A m=0 B m= 1 C m= 1 D m 1【 解 答 】 解 : 关 于 x 的 方 程 ( m2 1) x2+( m 1) x+7m2=0 是 一 元 一 次 方 程 , m2 1=0 且 m 1 0,解 得 : m= 1故 选 : B2 有 一 “ 数 值 转 换 机 ” 如 图 所 示 , 则 输 出 的 结 果 为 ( )A x B C D【 解 答 】 解 : 由 图 可 得 ,输 出 的 结 果 为 : ( x 2) 3= ,故 选 : C3 在 有 理 数 范 围 内 定 义 运 算 “ *” , 其 规 则 为 a*b= , 则 方 程 ( 2
14、*3) ( 4*x)=49 的 解 为 ( )A 3 B 55 C 56 D 55【 解 答 】 解 : 根 据 题 中 的 新 定 义 得 : ( ) =49,整 理 得 : 56+7x=441,解 得 : x=55,故 选 : D4 下 列 运 用 等 式 性 质 进 行 变 形 : 如 果 a=b, 那 么 a c=b c; 如 果 ac=bc,那 么 a=b; 由 2x+3=4, 得 2x=4 3; 由 7y= 8, 得 y= , 其 中 正 确 的有 ( )A 1 个 B 2 个 C 3 个 D 4 个【 解 答 】 解 : 如 果 a=b, 那 么 a c=b c, 正 确 ; 如
15、 果 ac=bc, 那 么 a=b( c 0) , 故 此 选 项 错 误 ; 由 2x+3=4, 得 2x=4 3, 正 确 ; 由 7y= 8, 得 y= , 故 此 选 项 错 误 ;故 选 : B5 已 知 关 于 x 的 方 程 2x a 5=0 的 解 是 x=b, 则 关 于 x 的 方 程 3x a+2b= 1的 解 为 ( )A x= 1 B x=1 C x=2 D x= 2【 解 答 】 解 : 把 x=b 代 入 方 程 2x a 5=0, 可 得 : 2b a 5=0,即 可 得 : a+2b=5,把 a+2b=5 代 入 3x a+2b= 1, 可 得 : 3x+5=
16、 1,解 得 : x= 2,故 选 : D6 如 图 , 边 长 为 a 的 正 方 形 中 阴 影 部 分 的 面 积 为 ( )A a2 a2 B a2 C a2 a2 D a2【 解 答 】 解 : 由 图 可 得 ,阴 影 部 分 的 面 积 为 : a2 ( ) 2=a2 a2,故 选 : A7 在 国 道 107 工 程 施 工 现 场 , 调 来 72 名 司 机 师 傅 参 加 挖 土 和 运 土 工 作 , 已 知 3名 司 机 师 傅 挖 出 的 土 1 名 司 机 师 傅 恰 好 能 开 车 全 部 运 走 , 怎 样 分 配 这 72 名 司机 师 傅 才 能 使 挖


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 期末 复习 人教版七 年级 数学 上册 第三 一元一次方程 单元 检测 试卷 答案 PDF
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
文档标签
- 人教版七
- 一元一次方程
- 2019-2020人教版七年级数学上册第三章
- 人教版七年级数学上册总复习专项测试题三含答案
- 人教版七年级数学上册总复习专项测试题一含答案
- 人教版七年级数学上册第三章一元一次方程单元练习题含答案
- 人教版七年级数学上册第三章一元一次方程单元测试含解析
- 湘教版数学七年级上册第3章 一元一次方程单元检测试卷1含答案
- 浙教版七年级数学上册第三章实数单元测试卷含答案
- 人教版初中数学七年级上册第三章一元一次方程单元检测题解析版
- 一元一次方程单元检测试卷含答案解析
- 人教版七年级上册数学第三章一元一次方程单元提升测试卷含答案
- 第三章一元一次方程 单元测试题含答案
- 湘教版数学七年级上册第3章 一元一次方程单元检测试卷2含答案
- 第三章一元一次方程 单元综合测试卷含答案解析
- 徐州市七年级数学上册期末测试
- 人教版七年级数学上册第三章一元一次方程单元测试题含答案
- 人教版七年电子课本 PDF
- 仁爱版英语七年级上册第三单位试卷
- 七年级数学上册举一反三系列



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-40440.html