1、 第 1 页 共 11 页【专题突破训练】湘教版九年级数学下册 第二章 圆 单元检测试卷一、单选题（共 10 题；共 30 分）1.已知 OA=5cm，以 O 为圆心，r 为半径作O若点 A 在 O 内，则 r 的值可以是（ ） A. 3cm B. 4cm C. 5cm D. 6cm2.已知O 的直径为 4，点 P 到点 O 的距离为 3，则下列对于点 P 与O 位置关系的说法正确的是（ ） A. 在圆上 B. 在圆内 C. 在圆外 D. 不确定3.如图，AB 是O 的直径，点 在圆上，且 .则 （ ） ABC=50 BACA. 50 B. 40 C. 30 D. 204.如图，O 是ABC
2、的外接圆，AD 是 O 的直径，连接 CD，若 O 的半径 r=5，AC=5 ，则 B 的度3数是（ ）A. 30 B. 45 C. 50 D. 605.如图，AB 是O 的直径，CD 是弦，CDAB 于 E，则下列结论不一定成立的是( )A. COEDOE B. CEDE C. OEBE D. 弧 BC=弧 BD6.在以 AB 为直径的O 中，AB=8，若 OP=5，则点 P 与O 的位置关系是（ ） A. 点 P 在O 内 B. 点 P 在O 上 C. 点 P 在O 外 D. 无法确定7.边长为 4cm 的正方形 ABCD 绕它的顶点 A 旋转 180，顶点 B 所经过的路线长为（ ）cm
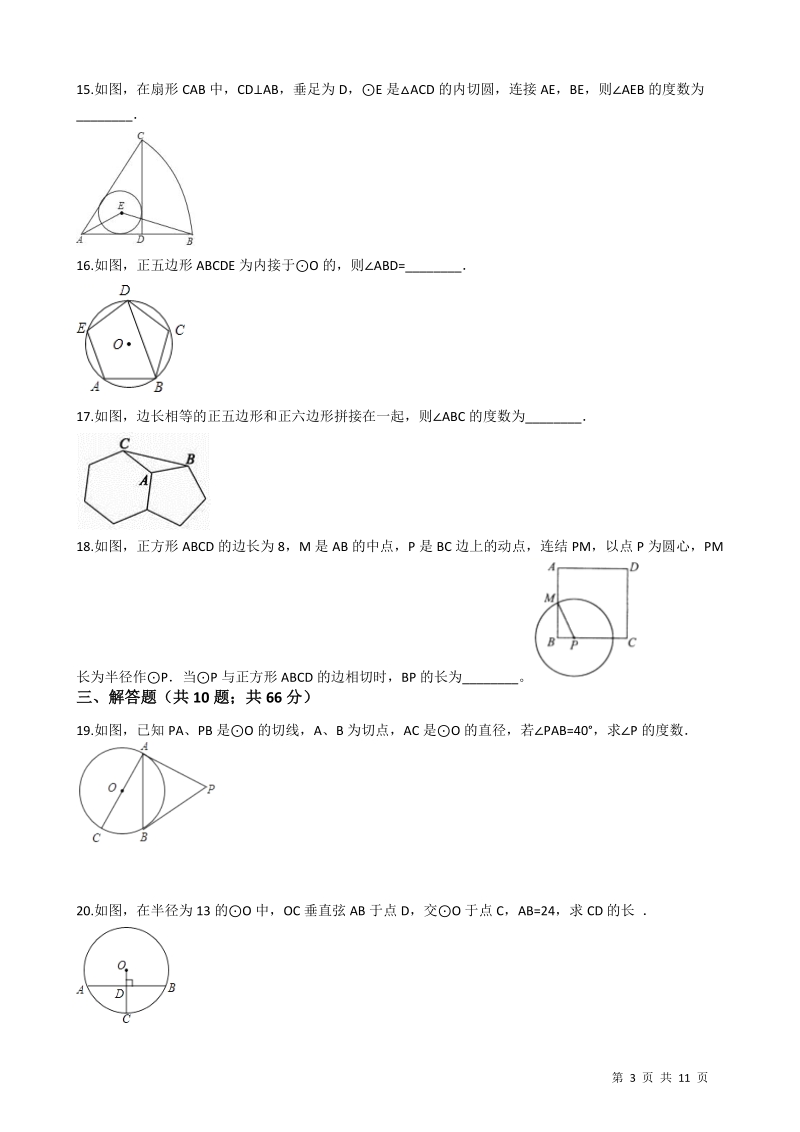
3、 A. 4 B. 3 C. 2 D. 第 2 页 共 11 页8.如图，AB 是O 的直径，BAC=30，CD AB 于点 E，BE=2，则 O 的半径为（ ）A. 8 B. 6 C. 4 D. 29.正六边形的两条对边之间的距离是 2 ，则它的边长是（ ） 3A. 1 B. 2 C. D. 2 3 310.如图，AB 是O 的直径，弦 CDAB 于点 P，CD=10cm，AP：PB=1：5，那么O 的半径是（ ） A. 5 cm B. 4 cm C. 3 cm D. 2 cm2 3 5 6二、填空题（共 8 题；共 24 分）11.已知扇形的圆心角为 120，弧长为 6，则它的半径为_ 12
4、.如图， 是 的直径， 是 上的点，过点 作 的切线交 的延长线于点 .若AB O C O C O AB DA=32，则 _度 D=13.如图,AB 是O 的直径,弦 CDAB 于点 E,若 AB=10,CD=6,则 BE=_.14.如图，AB 为O 的直径，弦 CDAB 于点 E，已知 CD=6，EB=1，则O 的半径为_第 3 页 共 11 页15.如图，在扇形 CAB 中，CD AB，垂足为 D， E 是ACD 的内切圆，连接 AE，BE，则 AEB 的度数为_16.如图，正五边形 ABCDE 为内接于 O 的，则ABD=_17.如图，边长相等的正五边形和正六边形拼接在一起，则 ABC
5、的度数为_18.如图，正方形 ABCD 的边长为 8，M 是 AB 的中点，P 是 BC 边上的动点，连结 PM，以点 P 为圆心，PM长为半径作P当P 与正方形 ABCD 的边相切时，BP 的长为_。三、解答题（共 10 题；共 66 分）19.如图，已知 PA、PB 是O 的切线，A 、B 为切点，AC 是O 的直径，若PAB=40，求P 的度数20.如图，在半径为 13 的O 中，OC 垂直弦 AB 于点 D，交O 于点 C，AB=24，求 CD 的长 第 4 页 共 11 页21.如图，在ABC 中，C=90，AE 平分BAC 交 BC 于 E，点 O 在 AB 上，以 OA 为半径的
6、圆，交 AB 于D，交 AC 于 C，且点 E 在O 上，连接 DE，BF 切 O 于点 F（1 ）求证：BE=BF ；（2 ）若O 的半径为 R，AG=R+1 ，CE=R1 ，求弦 AG 的长22.如图，在梯形 ABCD 中，ABCD， O 为内切圆，E 为切点（1 ）求证：AO 2=AEAD （2 ）若 AO=4cm，AD=5cm，求O 的面积 23.如图，AB 是O 的直径,BC 是 O 的弦，半径 ODBC,垂足为 E，若 BC= ，OE=3 ；63求：（1）O 的半径；（2 ）阴影部分的面积。 第 5 页 共 11 页24.已知如图，O 的内接ABC 中，AB=AC，弦 BD，CE
7、分别 ABC， ACB，且 BE=BC，求证：五边形AEBCD 是正五边形25.如图, ABC 内接于O, ADBC 于 D, AE 是O 的直径. 若 AB=6, AC=8, AE=11, 求 AD 的长.26.如图，AB 是O 的直径，C 是O 上的一点，DA 与O 相切于点 A，DA=DC= 3MISSING IMAGE: , （1 ）求证：DC 是 O 的切线；（2 ）若 CAB=30，求阴影部分的面积第 6 页 共 11 页27.如图，在O 中，F，G 是直径 AB 上的两点，C ，D ，E 是半圆上的三点，如果弧 AC 的度数为 60，弧BE 的度数为 20， CFA=DFB，DG
8、A= EGB求FDG 的大小28.如图，BC 是半圆 O 的直径，D 是弧 AC 的中点，四边形 ABCD 的对角线 AC、BD 交于点E，CE= ，CD=2.5(1)求直径 BC 的长；(2)求弦 AB 的长. 第 7 页 共 11 页答案解析部分一、单选题1.【答案】D 2.【答案】C 3.【答案】B 4.【答案】D 5.【答案】C 6.【答案】C 7.【答案】A 8.【答案】C 9.【答案】B 10.【 答案】C 二、填空题11.【 答案】9 12.【 答案】26 13.【 答案】1 14.【 答案】5 15.【 答案】135 16.【 答案】72 17.【 答案】24 18.【 答案】
9、3 或 43三、解答题19.【 答案】解： PA 和 PB 为切线 ，A,B 是切点PA=PBPBA=PAB=40P=180（ PAB+PBA）=100 20.【 答案】解：连接 O A ， ， ，OC AB AB=24 ，AD=12AB=12在 中，RtAOD ， ，OA=13 AD=12第 8 页 共 11 页 ，OD=5 CD=OC-OD=13-5=821.【 答案】证明：（1）连接 DG、OE ，交于点 HAE 平分BAC 交 BC 于 E，CAE=DAE，OA=OE，OAE=OEA，CAE=OEA，ACOE，OEB=C=90，OEBC，BC 是圆的切线，BE=BF；（2 ）解：AB
10、是直径，AGD=90，C=90，GDBC，OEBC，OEGD，GH=DH，AGD=90，C=90，OEBC，四边形 GCEH 是矩形，GH=CE=R1，GD=2（R1）=2R 2，在直角三角形 AGD 中，AG 2+GD2=AD2 ， 即（R+1） 2+（2R2） 2=（2R） 2解得 R1=5，R 2=1（舍去），AG=R+1=5+1=6；22.【 答案】（1）证明：根据切线长定理可知：OAE+ODA= （BAD+ADC）=90，12AOD=90，第 9 页 共 11 页OAE=OAE， AOD=AEO=90，AOEADO，AEOA=OAAD即 AO2=AEAD（2 ）解：在 RtAOD 中
11、，OD= =3，AD2-AO2SAOD= ADEO= AOOD12 12即 5EO=43，EO= ，125OE 是O 的半径，S 圆 O=r2= 1442523.【 答案】解：（1） BC 是 O 的弦，半径 ODBC，BC= ，CE= BC= .6312 33在 RtCOE 中，由勾股定理得， ,CO= CE2-OE2= (33)2+32=6O 的半径是 6.（2 ） 在 RtCOE 中，CEO=90 ，CO=2OE，ECO=30 AB 是O 的直径，ACB=90.ACO=60OA=OC，ACO 是等边三角形. AOC=60.S 阴影 =S 扇形 ACO-SAOC= .60 62360-12
12、6632=6 -93答：阴影部分的面积是 6 -9324.【 答案】证明： AB=AC，ABC=ACB，弦 BD， CE 分别平分ABC ，ACB，ABD=DBC=ECB=ACE，BE=BC，BE= BCBEC=BCE，BCA=BEC，ABD=DBC=ECB=ACE=BAC， ，AE= AD= DC= BC= BE第 10 页 共 11 页五边形 AEBCD 是正五边形25.【 答案】解：连接 CE，则 E=B，AE 是 O 的直径，ACE=90，又 ADBC，ACE=ADB=90，ACEADB， ，AEAB=ACAD即 ，116=8AD解得 AD= 481126.【 答案】 27.【 答案】
13、解：如图：作点 C 关于 AB 的对称点 M，点 E 关于 AB 的对称点 N，连结 CM、FM，设 CM 交AB 于点 Q，依题可得 ABCM，CQ=MQ ，CFA=AFM，又CFA=DFB，AFM=DFB，D、F、M 三点共线，同理可得 D、G、N 三点共线，又 弧 AC=60，弧 BE=20，弧 AM=弧 AC=60，弧 BN=弧 BE=20，弧 MN=180-60-20=100，第 11 页 共 11 页FDG= 100=50.1228.【 答案】解：(1)BC 是半圆 O 的直径，BDC=90 0.CE= ，CD=2，根据勾股定理，得 DE=1.5D 是弧 AC 的中点，AD=CD=2.易证ADE BCE， ,即 ，解得 BC= .ADBC=DECE2BC= 15 25(2) 易证ABE DCE, .AEAB=DEDC=12设 AE=x , 则 AB=2x，AC=x+ ，5AB2+AC2=BC2,(2x)2+(x+ )2=( )2 ， 解得 x= .5 25-258510x0，x= .AB=2x= . 355 655
