1、 第 1 页 共 19 页【易错题解析】湘教版九年级数学上册 第一章 反比例函数 单元检测试卷一、单选题（共 10 题；共 30 分）1.下列函数中，是反比例函数的是( ) A. y=2x B. y= C. y= D. y=kx 2x x2【答案】C 【考点】反比例函数的定义 【解析】【分析】反比例函数的定义：一般地，形如 的函数叫做反比例函数.y=kx(k 0)A、y= 2x，D 、y= ，是正比例函数，B、y= ，缺少 的条件，故错误；x2 kx k 0C、 y= ，符合反比例函数的定义，本选项正确.2x【点评】本题属于基础应用题，只需学生熟练掌握反比例函数的定义，即可完成.2.已知反比例
2、函数的图象经过点（1 ，2），则它的解析式是（ ）A. y= B. y= C. y= D. y=12x 2x 2x 1x【答案】B 【考点】反比例函数图象上点的坐标特征 【解析】 【 分析 】 设解析式为 y （k0) ，由于反比例函数的图象经过点（-1 ，2)，代入反比例函数即可kx求得 k 的值【解答】设反比例函数图象设解析式为 y ， kx将点（-1，2)代入 y 得，kxk=-12=-2，则函数解析式为 y=- 2x故选 B【 点评 】 本题考查了待定系数法求函数解析式，将点（-1，2) 代入反比例函数，求出系数 k 是解题的关键3.在反比例函数 的每一条曲线上，y 都随着 x 的增大
3、而增大，则 k 的值可以是（ ） y=1-kxA. 1 B. 0 C. 1 D. 2【答案】D 【考点】反比例函数的性质 第 2 页 共 19 页【解析】【分析】先根据已知反比例函数的增减性判断出 1-k 的符号，再求出 k 的取值范围即可【解答】y 都随 x 的增大而增大，此函数的图象在二、四象限，1-k0，k1故 k 可以是 2，故选 D【点评】本题主要考查反比例函数的性质的知识点，此题属开放行题目，答案不唯一，解答此题的关键是根据题意判断出函数图象所在的象限，再根据反比例函数的性质解答即可4.（2017广东）如图，在同一平面直角坐标系中，直线 y=k1x（k 10）与双曲线 y= （k
4、20）相交于k2xA，B 两点，已知点 A 的坐标为（1，2），则点 B 的坐标为（ ） A. （1， 2） B. （ 2，1 ） C. （1， 1） D. （ 2，2 ）【答案】A 【考点】反比例函数与一次函数的交点问题 【解析】【解答】解：点 A 与 B 关于原点对称， B 点的坐标为（1 ，2）故选：A【分析】反比例函数的图象是中心对称图形，则经过原点的直线的两个交点一定关于原点对称5.已知函数 y=（ m2） 是反比例函数，图象在第一、三象限内，则 m 的值是（ ） xm2-10A. 3 B. -3 C. 3 D. -13【答案】A 【考点】反比例函数的定义，反比例函数的性质 【解析】
5、【解答】解：函数 y=（m 2） 是反比例函数，xm2-10m210=1，解得，m 2=9，m=3，当 m=3 时，m 20，图象位于一、三象限；当 m=3 时，m20 ，图象位于二、四象限；第 3 页 共 19 页故选 A【分析】根据反比例函数的定义建立关于 m 的一元二次方程，再根据反比例函数的性质解答6.一次函数 ykxb 与反比例函数 y 的图象在同一直角坐标系下的大致图象如图所示，则 k、b 的取kx值范围是( )A. k 0，b 0 B. k0，b0 C. k0，b0 D. k0 ，b0【答案】C 【考点】反比例函数的性质，一次函数的性质 【解析】【解答】一次函数 y=kx+b 的
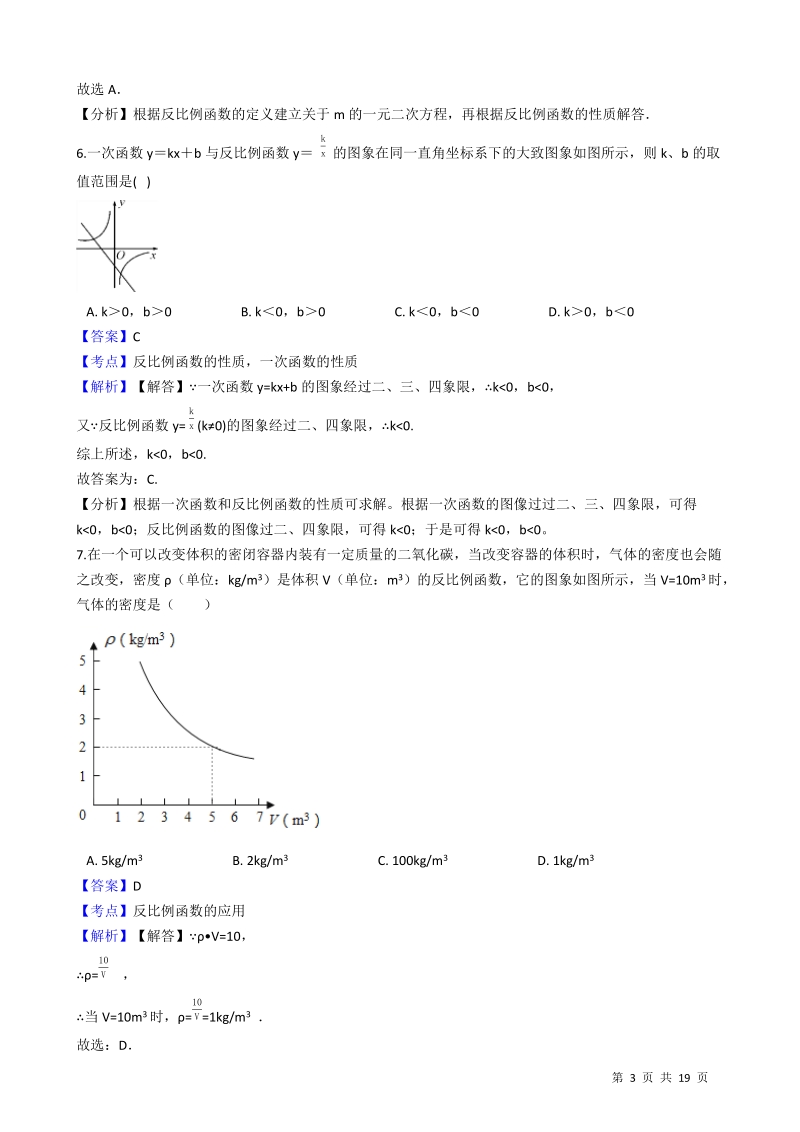
6、图象经过二、三、四象限，k0，b0，又 反比例函数 y= (k0)的图象经过二、四象限，k0.kx综上所述，k0，b0.故答案为：C.【分析】根据一次函数和反比例函数的性质可求解。根据一次函数的图像过过二、三、四象限，可得k0， b0；反比例函数的图像过二、四象限，可得 k0；于是可得 k0，b0。7.在一个可以改变体积的密闭容器内装有一定质量的二氧化碳，当改变容器的体积时，气体的密度也会随之改变，密度 （单位：kg/m 3）是体积 V（单位：m 3）的反比例函数，它的图象如图所示，当 V=10m3 时，气体的密度是（ ）A. 5kg/m3 B. 2kg/m3 C. 100kg/m3 D. 1
7、kg/m3【答案】D 【考点】反比例函数的应用 【解析】【解答】V=10，= ， 10V当 V=10m3 时， = =1kg/m3 10V故选：D第 4 页 共 19 页【 分析 】 根据题意：密度 与体积 V 成反比例函数，且过点（5 ，2) ，故 V=10；故当 V=10m3 时，气体的密度是 10 V =1kg/m3 现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系，然后利用待定系数法求出它们的关系式8.如图，函数 y1= （k 10）与 y2=k2x（k 20）的图象 Ox 交于 A、B 两点，且 A（ 1，3）若 y1y 2 ， k1x则 x
8、的取值范围是（ ）A. 1x0 B. x1 或 0x1 C. 1x1 D. 1x 0 或 x1【答案】D 【考点】反比例函数与一次函数的交点问题 【解析】【解答】解：函数 y1= （k 10）与 y2=k2x（k 20）的图象 Ox 交于 A、B 两点，且 A（ 1，3），k1xB（1， 3），y1y 2 ， 此时 x 的取值范围是1x 0 或 x1，故选 D【分析】根据 A、B 的横坐标，结合图象即可得出当 y1y 2 时 x 的取值范围9.如果反比例函数 y= 的图象在所在的每个象限 y 都是随着 x 的增大而减小，那么 m 的取值范围是1-mx（ ） A. m1 B. m1 C. m1
9、D. m1【答案】B 【考点】反比例函数的性质 【解析】【解答】解：由题意得：1 m0， 解得：m1，故选：B【分析】根据反比例函数的性质可得 1m0，再解即可第 5 页 共 19 页10.如图，点 A 在双曲线 y= 上，且 OA=4，过点 A 作 ACx 轴，垂足为 C，OA 的垂直平分线交 OC 于点kxB，如果 AB+BCAC=2，则 k 的值为（ ） A. 82 B. 8+2 C. 3 D. 67 7【答案】D 【考点】线段垂直平分线的性质，勾股定理，反比例函数图象上点的坐标特征 【解析】【解答】解：设点 A 的坐标为（x，y）， OA=4，x2+y2=16，OA 的垂直平分线交 O
10、C 于 B，AB=OB，AB+BCAC=OB+BC+AC=OC+AC=xy=2，由得：xy=6，点 A 在双曲线 y= 上，kxk=6故选：D【分析】首先设点 A 的坐标为（x，y），由 OA=4，可得 x2+y2=16，由题意得出 xy=2，由得出 xy=6，即可得出结果二、填空题（共 10 题；共 30 分）11.点 P(2m3，1) 在反比例函数 y 的图象上，则 m _ 1x【答案】2 【考点】反比例函数图象上点的坐标特征 【解析】【解答】根据点 P 在反比例函数 y 的图像上，可直接代入可得 ，解得 2m-3=1，1x 1= 12m-3即 m=2.【分析】将点 p 代入反比例函数的解
11、析式，从而得到一个关于 m 的方程，求解得出 m 的值。12.长方体的体积为 103 m3 ， 底面积为 S，高度为 d，则 S 与 d 之间的函数关系式为_；当S 500 时，d_ 【答案】S ；2 103d【考点】反比例函数的实际应用 第 6 页 共 19 页【解析】【解答】v sd，s= ,103d当 s=500 时，代入 s= 中得，d=2;103d故答案是：s= ,2。103d【分析】现实生活中存在大量成反比例函数的两个变量，解答该类问题的关键是确定两个变量之间的函数关系然后再根据题意进行解答.由容积=底面积 深度可列出底面积 s（m 2）与其深度 d（m）之间的函数关系； 把 S=
12、500 代入 s 与 d 之间的函数关系式，即可求得施工队施工时应向下掘进的深度.13.已知 y 与 成反比例，当 y=1 时，x=4，则当 x=2 时，y=_ x【答案】 2【考点】反比例函数的定义 【解析】【解答】解：由于 y 与 成反比例，可以设 y= ， xkx把 x=4，y=1 代入得到 1= ，k2解得 k=2，则函数解析式是 y= ，2x把 x=2 代入就得到 y= 2故答案为： 2【分析】此题可先根据反比例函数的定义设出其解析式，再利用待定系数法求解，最后代入求值14.如图，点 A 在双曲线 y （x0）上，点 B 在双曲线 y （x0）上，且 ABy 轴，点 P 是 y 轴上
13、2x 4x的任意一点，则PAB 的面积为 _【答案】1. 【考点】反比例函数系数 k 的几何意义 【解析】【解答】连接 OA，OB，延长 BA 交 x 轴于点 C，则 SOAC=1，S OBC=2，所以 SPBA=SOAB=SOBC-SOAC=1.第 7 页 共 19 页【分析】连接 OA，OB，延长 BA 交 x 轴于点 C，利用反比例函数的比例系数 K 的几何意义知 SOAC=1，S OBC=2，从而利用 SPBA=SOAB=SOBC-SOAC 得出答案。15.如图，点 A 在函数 y (x0) 的图像上，点 B 在 x 轴正半轴上， OAB 是边长为 2 的等边三角形，则kxk 的值为_
14、 【答案】 3【考点】待定系数法求反比例函数解析式，等边三角形的性质 【解析】【解答】解：过点 A 作 ACOB，OAB 为正三角形，边长为 2，OC=1， AC= ， 3k=1 = 3 3【分析】过点 A 作 ACOB，根据OAB 是边长为 2 的等边三角形，求出 OC、AC 的长，就可得出点 A 的坐标，利用待定系数法求出 k 的值。16.如图，点 A 在反比例函数 上，AB x 轴于点 B，且AOB 的面积是 4，则 k 的值是_y=kx【答案】-8 【考点】反比例函数系数 k 的几何意义 【解析】【解答】ABx 轴，SAOB= |k|=4，12k0，第 8 页 共 19 页k=8故答案
15、为：8【分析】根据反比例函数的 k 的几何意义可求解。S AOB= |k|=4，则 k= 8，由图知 k0，则 k=812 17.反比例函数 y= （k0）的图象与经过原点的直线 l 相交于 A、B 两点，已知 A 点的坐标为（2，1），kx那么 B 点的坐标为_ 【答案】（2， 1） 【考点】反比例函数与一次函数的交点问题 【解析】【解答】解：点 A（2，1）与 B 关于原点对称， B 点的坐标为（ 2，1 ）故答案是：（2 ，1）【分析】反比例函数的图象是中心对称图形，则经过原点的直线的两个交点一定关于原点对称18.双曲线 y1、y 2 在第一象限的图象如图所示，y 2= ，过 y1 上的
16、任意一点 A 作 x 轴的平行线交 y2 于点12xB，交 y 轴于点 C，如果 SAOB=4，那么 y1 的函数表达式是_ 【答案】y 1= 4x【考点】反比例函数系数 k 的几何意义，待定系数法求反比例函数解析式 【解析】【解答】解：设 y1= ， ABx 轴，kxSOBC= 12=6，S OAC= k，12 12SAOB=6 k=4，12k=4，y1 的解析式是 y1= 4x故答案为 y1= 4x【分析】设 y= ，根据反比例函数 xy=k（k0）系数 k 的几何意义得到 SOAC= k，S OBC= 12=6，由 Skx 12 12AOB=4 得到 6 k=4，然后解方程即可12第 9
17、 页 共 19 页19.（ 2017云南）已知点 A（a，b）在双曲线 y= 上，若 a、b 都是正整数，则图象经过 B（a ，0）、5xC（ 0，b）两点的一次函数的解析式（也称关系式）为_ 【答案】y= 5x+5 或 y= x+1 15【考点】待定系数法求一次函数解析式，反比例函数图象上点的坐标特征 【解析】【解答】点 A（a，b ）在双曲线 y= 上，5xab=5，a、b 都是正整数，a=1，b=5 或 a=5，b=1设经过 B（a ，0 ）、C（0，b）两点的一次函数的解析式为 y=mx+n当 a=1，b=5 时，由题意，得 ，解得 ，m+n=0n=5 m= -5n=5y=5x+5；当
18、 a=5，b=1 时，由题意，得 ，解得 ，5m+n=0n=1 m= -15n=1y= x+115则所求解析式为 y=5x+5 或 y= x+115故答案为：y= 5x+5 或 y= x+115【分析】根据反比例函数图像上点的特征结合题意得出 ab=5，再由 a、b 都是正整数，得出 a=1，b=5 或a=5， b=1设经过 B（a ，0 ）、C（0，b）两点的一次函数的解析式为 y=mx+n当 a=1，b=5 时，由题意得到关于 m 与 n 的二元一次方程组 ，解得 ，所以 y=5x+5；m+n=0n=5 m= -5n=5当 a=5，b=1 时，由题意得到关于 m 与 n 的二元一次方程组
19、，解得 ，所以 y= x+15m+n=0n=1 m= -15n=1 15从而得出所求解析式为 y=5x+5 或 y= x+115第 10 页 共 19 页20.如图，已知第一象限内的点 A 在反比例函数 上，第二象限的点 B 在反比例函数 上，且y=2x y=kxOA OB， ，则 k 的值为_ sinA=33【答案】 -1【考点】反比例函数系数 k 的几何意义 【解析】【解答】作 BEx 轴于 E，AFx 轴于 F，点 A 在反比例函数 上，y=2xOAOB， S AOF=1,又 BOE+ AOF=90, BOE+ OBE=90，AOF=OBE，OBEAOF，k=1， sinA= 33， O
20、BOA= 12， S BOES AOF=12， S BOE=12，故答案为：1.【分析】作 BEx 轴于 E，AFx 轴于 F，根据点 A 的位置可得 OBEAOF，又由S AOF=1,再证得从而可求得 k=1.sinA=33， 得到 OBOA= 12， 那么 S BOES AOF=12，即 S BOE=12，三、解答题（共 8 题；共 60 分）第 11 页 共 19 页21.如图，已知在平面直角坐标系 xOy 中，O 是坐标原点，点 A 是函数 y1= （x0）图象上一点，AO 的4x延长线交函数 y2= （x0 ，k0）的 y2 图象于点 B，BCx 轴，若 SABC= ，求函数 y2
21、k2x 152【答案】解：设 A（m， ）（m0）， 直线 AB 的解析式为 y=ax（k0），A（m ， ），ma= ，解得 a= ，直线 AB 的解析式为 y= xAO 的延长线交函数 y= 的图象于点 B，B（ mk， ），ABC 的面积等于 ，CB x 轴， （ ） （ mk+|m|）= ，解得 k1=5（舍去），k 2=3，y2= 【考点】反比例函数与一次函数的交点问题 第 12 页 共 19 页【解析】【分析】设 A（m， ）（m0），则可得到直线 AB 的解析式为 y= x再利用反比例函数与4m 4m2一次函数的交点问题可表示出 B（ mk， ），则利用三角形面积公式得到 （ ）
22、（ mk+|m|）12 2km 12 2km 12= ，解得 k1=5（舍去），k 2=3，于是得到 y2= 152 9x22.如图，一次函数 y=x+5 的图象与反比例函数 y= （k0 ）在第一象限的图象交于 A（1 ，n）和 B 两点kx（1 ）求反比例函数的解析式；（2 ）在第一象限内，当一次函数 y=x+5 的值大于反比例函数 y= （k0）的值时，写出自变量 x 的取值范kx围【答案】解：（1） 一次函数 y=x+5 的图象过点 A（1， n），n=1+5，n=4，点 A 坐标为（1，4），反比例函数 y= （k0）过点 A（1，4 ），kxk=4，反比例函数的解析式为 y= ；4
23、x（2 ）联立 ，y= -x+5y=4x 解得 或 ，x=1y=4 x=4y=1即点 B 的坐标（4，1 ），若一次函数 y=x+5 的值大于反比例函数 y= （k0）的值，kx则 1x4 【考点】反比例函数与一次函数的交点问题 【解析】【分析】（1）首先求出点 A 的坐标，进而即可求出反比例函数系数 k 的值；第 13 页 共 19 页（2 ）联立反比例函数和一次函数解析式，求出交点 B 的坐标，结合图形即可求出 x 的取值范围23.如图，正比例函数 y= x 的图象与反比例函数 y= 的图象分别交于 M，N 两点，已知点 M（ 2，m）12 kx（1 ）求反比例函数的表达式；（2 ）点 P
24、 为 y 轴上的一点，当 MPN 为直角时，直接写出点 P 的坐标【答案】解：（1） 点 M（2，m）在正比例函数 y= x 的图象上，12m= （2 ）=1 ，12M（2，1 ），反比例函数 y= 的图象经过点 M（2 ，1），kxk=21=2反比例函数的解析式为 y= 2x（2 ） 正比例函数 y= x 的图象与反比例函数 y= 的图象分别交于 M，N 两点，点 M（ 2，1），12 kxN（2 ，1），点 P 为 y 轴上的一点，设 P（0，m），MPN 为直角，MPN 是直角三角形，（ 0+2） 2+（m1 ） 2+（02） 2+（m+1） 2=（2+2） 2+（ 11） 2 ， 解得
25、 m= 5点 P 的坐标为（0， ）或（0， ） 5 5第 14 页 共 19 页【考点】反比例函数与一次函数的交点问题 【解析】【分析】（1）把 M（2，m ）代入函数式 y= x 中，求得 m 的值，从而求得 M 的坐标，代入 y=12可求出函数解析式；kx（2 ）根据 M 的坐标求得 N 的坐标，设 P（0 ，m），根据勾股定理列出关于 m 的方程，解方程即可求得m 进而求得 P 的坐标24.如图，在矩形 OABC 中，OA=3，OC=2，F 是 AB 上的一个动点（F 不与 A，B 重合），过点 F 的反比例函数 y= （k 0）的图象与 BC 边交于点 E当 F 为 AB 的中点时，
26、求该函数的解析式.kx【答案】解：在矩形 OABC 中，OA=3 ，OC=2 ， B（3 ，2）F 为 AB 的中点，F（3，1）点 F 在反比例函数 （k 0）的图象上， k=3，该函数的解析式为 （x0） y=kx y=3x【考点】待定系数法求反比例函数解析式，矩形的性质 【解析】【分析】根据矩形的性质由矩形的边长 OA=3， OC=2 得出 B 点的坐标，又 F 为 AB 的中点，故能得出 F 点的坐标，然后将 F 点的坐标代入反比例函数的解析式，即可求出比例系数 K 的值，从而得出反比例函数的解析式。25.已知正比例函数 y=2x 的图象与反比例函数 y= （k0）在第一象限的图象交于
27、 A 点，过 A 点作 x 轴的垂kx线，垂足为 P 点，已知 OAP 的面积为 1（1 ）求反比例函数的解析式；（2 ）如果点 B 为反比例函数在第一象限图象上的点（点 B 与点 A 不重合），且点 B 的横坐标为 2，在 x轴上求一点 M，使 MA+MB 最小【答案】解：（1）设 A 点的坐标为（x，y ），则 OP=x，PA=y ，OAP 的面积为 1， xy=1，xy=2，即 k=2，12第 15 页 共 19 页反比例函数的解析式为：y= 2x（2 ）作点 A 关于 x 轴的对称点 A，连接 AB，交 x 轴于点 M，MA+MB 最小，点 B 的横坐标为 2，点 B 的纵坐标为 y=
28、 =1，22两个函数图象在第一象限的图象交于 A 点，2x= ，x1，y=2 ，2xA 点的坐标（1，2），A 关于 x 轴的对称点 A（1，2 ），设直线 AB 的解析式为 y=kx+b，k+b= -22k+b=1解得 ，k=3b= -5直线 y=3x5 与 x 轴的交点为（ ，0），53则 M 点的坐标为（ ，0） 53【考点】反比例函数与一次函数的交点问题 【解析】【分析】（1）设出 A 点的坐标，根据 OAP 的面积为 1，求出 xy 的值，得到反比例函数的解析式；（2 ）作点 A 关于 x 轴的对称点 A，连接 AB，交 x 轴于点 M，得到 MA+MB 最小时，点 M 的位置，求出
29、直线 AB 的解析式，得到它与 x 轴的交点，即点 M 的坐标26.已知双曲线 与直线 相交于 A、B 两点第一象限上的点 M（m，n）（在 A 点左侧）是双曲y=kx y=14x线 上的动点过点 B 作 BDy 轴交 x 轴于点 D过 N（0，n）作 NCx 轴交双曲线 于点 E，交y=kx y=kxBD 于点 C第 16 页 共 19 页（1 ）若点 D 坐标是（ 8，0），求 A、B 两点坐标及 k 的值（2 ）若 B 是 CD 的中点，四边形 OBCE 的面积为 4，求直线 CM 的解析式 【答案】（1） D（8，0），B 点的横坐标为 8，代入 中，得 y=2y=14xB 点坐标为（
30、 8，2 ）A、B 两点关于原点对称，A（8 ，2）k=xy=82=16；（2 ） N（0 ，n），B 是 CD 的中点，A、B、M、E 四点均在双曲线上，mn=k， B（ 2m， ），C（ 2m，n），E（m，n）n2S 矩形 DCNO=2mn=2k，S DBO= ，S OEN= ，12mn=12k 12mn=12kS 四边形 OBCE=S 矩形 DCNOSDBOSOEN=k=4k=4B（ 2m， ）在双曲线 与直线 上n2 y=4x y=14x 得 或 （舍去）(-2m)(-n2)=414(-2m)= -n2 m1=2n1=2 m2= -2n2= -2C（4，2），M（2，2）设直线 CM
31、 的解析式是 y=ax+b，把 C（4， 2）和 M（2，2）代入得：第 17 页 共 19 页解得 -4a+b= -22a+b=2 a=b=23直线 CM 的解析式是 y=23x+23【考点】反比例函数与一次函数的交点问题 【解析】【分析】此题主要考查了待定系数法函数解析式以及一次函数与反比例函数交点的性质，根据四边形 OBCE 的面积为 4 得出 k 的值是解决问题的关键（1 ）根据 B 点的横坐标为 8，代入 中，得 y=2，得出 B 点的坐标，即可得出 A 点的坐标，再根据y=14xk=xy 求出即可；（2 ）根据 S 矩形 DCNO=2mn=2k，S DBO= ， SOEN= ， 即
32、可得出 k 的值，进而得出 B，C12mn=12k 12mn=12k点的坐标，再求出解析式即可27.如图：一次函数的图象与反比例函数 的图象交于 A（2,6）和点 B（4,n）y=kx（1 ）求反比例函数的解析式和 B 点坐标（2 ）根据图象回答,在什么范围时,一次函数的值大于反比例函数的值. 【答案】解：（1）把 A（2,6）代入 得：k=12,y=kx即反比例函数的解析式是： ,y= -12x把 B（4,n）代入反比例函数的解析式得： ,n= -124= -3即 B 的坐标是（4,3 ）;（2 ） 一次函数和反比例函数的交点坐标是（4, 3）和（2,6）,一次函数的值大于反比例函数的值时,
33、x 的范围是 x2 或 0x4 【考点】待定系数法求一次函数解析式，待定系数法求反比例函数解析式，反比例函数与一次函数的交点问题 【解析】【分析】（1）把 A 的坐标代入反比例函数的解析式即可求出反比例函数的解析式,把 B 的坐标代入即可求出 B 的坐标;（2 ）根据 A、B 的坐标结合图象即可得出答案第 18 页 共 19 页28.心理学家研究发现，一般情况下，一节课 40 分钟中，学生的注意力随教师讲课的变化而变化开始上课时，学生的注意力逐步增强，中间有一段时间学生的注意力保持较为理想的稳定状态，随后学生的注意力开始分散经过实验分析可知，学生的注意力指标数 y 随时间 x（分钟）的变化规律
34、如下图所示（其中 AB、 BC 分别为线段，CD 为双曲线的一部分）：（1 ）开始上课后第五分钟时与第三十分钟时相比较，何时学生的注意力更集中？（2 ）一道数学竞赛题，需要讲 19 分钟，为了效果较好，要求学生的注意力指标数最低达到 36，那么经过适当安排，老师能否在学生注意力达到所需的状态下讲解完这道题目？【答案】解：（1）设线段 AB 所在的直线的解析式为 y1=k1x+20，把 B（10，40）代入得，k 1=2，y1=2x+20设 C、D 所在双曲线的解析式为 y2= ，k2x把 C（25，40）代入得，k 2=1000，y2=1000x当 x1=5 时，y 1=25+20=30，当 x2=30,y2= = ，1000301003y1y 2第 30 分钟注意力更集中（2 ）令 y1=36，36=2x+20，x1=8令 y2=36，36= ，1000xx2= 27.810003627.88=19.819，经过适当安排，老师能在学生注意力达到所需的状态下讲解完这道题目 第 19 页 共 19 页【考点】根据实际问题列反比例函数关系式 【解析】【分析】（1）先用代定系数法分别求出 AB 和 CD 的函数表达式，再分别求第五分钟和第三十分钟的注意力指数，最后比较判断；（2 ）分别求出注意力指数为 36 时的两个时间，再将两时间之差和 19 比较，大于 19 则能讲完，否则不能
