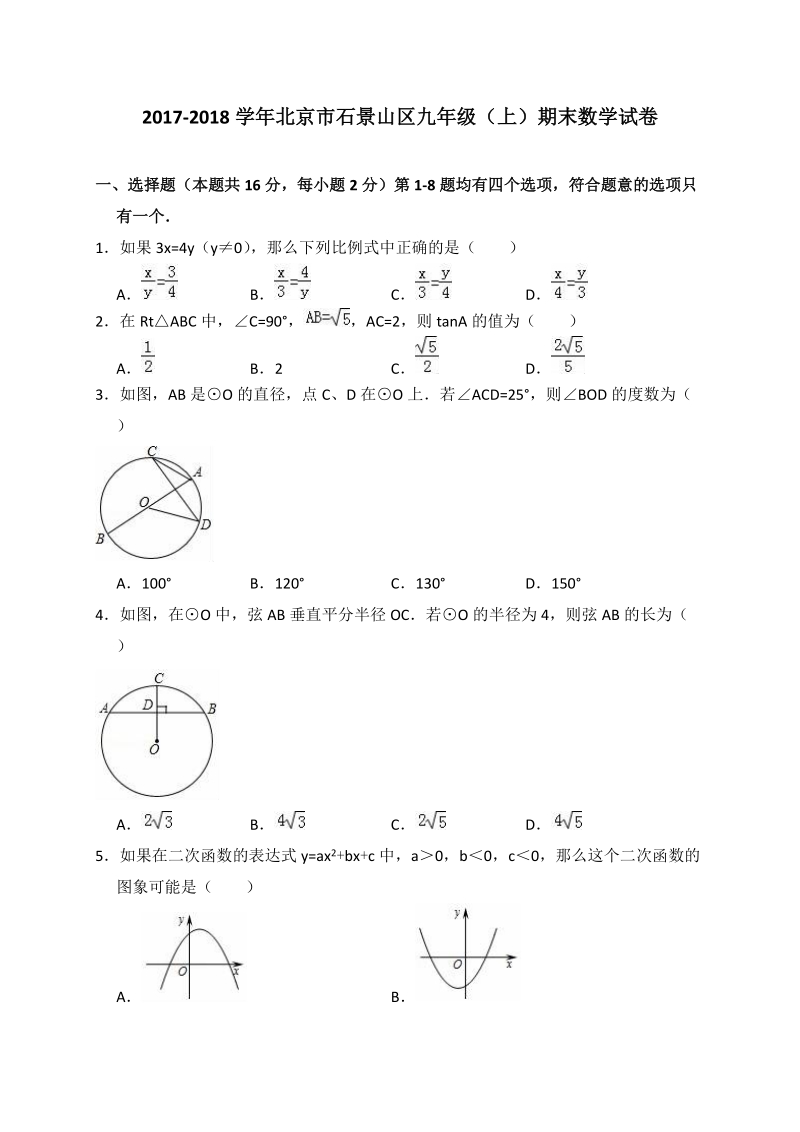
1、2017-2018 学年北京市石景山区九年级（上）期末数学试卷一、选择题（本题共 16 分，每小题 2 分）第 1-8 题均有四个选项，符合题意的选项只有一个1如果 3x=4y（y0） ，那么下列比例式中正确的是（ ）A B C D2在 RtABC 中，C=90， ，AC=2，则 tanA 的值为（ ）A B2 C D3如图，AB 是O 的直径，点 C、D 在O 上若ACD=25，则BOD 的度数为（ ）A100 B120 C130 D1504如图，在O 中，弦 AB 垂直平分半径 OC若 O 的半径为 4，则弦 AB 的长为（ ）A B C D5如果在二次函数的表达式 y=ax2+bx+c
2、中，a0，b0，c0，那么这个二次函数的图象可能是（ ）A BC D6若二次函数 y=x2+2x+m 的图象与坐标轴有 3 个交点，则 m 的取值范围是（ ）Am 1 Bm1 Cm1 且 m0 Dm1 且 m07如图，将函数 的图象沿 y 轴向上平移得到新函数图象，其中原函数图象上的两点 A（1，m） 、B （4，n）平移后对应新函数图象上的点分别为点A、B若阴影部分的面积为 6，则新函数的表达式为（ ）A BC D8如图，点 M 为ABCD 的边 AB 上一动点，过点 M 作直线 l 垂直于 AB，且直线 l 与ABCD 的另一边交于点 N当点 M 从 AB 匀速运动时，设点 M 的运动时间
3、为 t，AMN 的面积为 S，能大致反映 S 与 t 函数关系的图象是（ ）A BC D二、填空题（本题共 16 分，每小题 2 分）9如果两个相似三角形的周长比为 2：3，那么这两个相似三角形的面积比为 10如图，在ABC 中，点 D、E 分别在边 AB、AC 上若ADE=C， AB=6，AC=4 ，AD=2，则 EC= 11如图，扇形的圆心角AOB=60，半径为 3cm若点 C、D 是 的三等分点，则图中所有阴影部分的面积之和是 cm 212 “平改坡 ”是指在建筑结构许可条件下，将多层住宅的平屋顶改建成坡屋顶，并对外立面进行整修粉饰，达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为如图
4、是某小区对楼顶进行“平改坡” 改造的示意图根据图中的数据，如果要使坡面 BC的坡度达到 1：1.2，那么立柱 AC 的长为 米13如图，一次函数 y1=kx+b 的图象与反比例函数 y2= 的图象相交于点 A 和点B当 y1y 20 时，x 的取值范围是 14如图，在 RtABC 中，C=90 ，AB=10，若以点 C 为圆心，CB 长为半径的圆恰好经过 AB 的中点 D，则 AC 的长等于 15如图，在平面直角坐标系 xOy 中，ABC 经过若干次图形的变化（平移、轴对称、旋转）得到DEF ，写出一种由 ABC 得到DEF 的过程： 16石景山区八角北路有一块三角形空地（如图 1）准备绿化，
5、拟从点 A 出发，将ABC 分成面积相等的三个三角形，栽种三种不同的花草下面是小美的设计（如图 2） 作法：（1）作射线 BM；（2）在射线 BM 上顺次截取 BB1=B1B2=B2B3；（3）连接 B3C，分别过 B1、B 2 作 B1C1B 2C2B 3C，交 BC 于点 C1、C 2；（4）连接 AC1、AC 2则 请回答， 成立的理由是： ； 三、解答题（本题共 68 分）解答应写出文字说明，演算步骤或证明过程.17 （5 分）计算：3tan30 cos245+ 2sin6018 （5 分）用配方法求二次函数 y=x210x+3 的顶点坐标19 （5 分）在 RtABC 中，C=90
6、，A、B 、C 的对边分别为 a、b、c若a=2，sin ，求 b 和 c20 （5 分）小红和小丁玩纸牌游戏：如图是同一副扑克中的 4 张牌的正面，将它们正面朝下洗匀后放在桌上，小红先从中抽出一张，小丁从剩余的 3 张牌中也抽出一张比较两人抽出的牌面上的数字，数字大者获胜（1）请用树状图或列表法表示出两人抽牌可能出现的所有结果；（2）这个游戏公平吗？请说明理由21 （5 分）如图，小明想测量山的高度他在点 B 处仰望山顶 A，测得仰角ABN=30，再向山的方向（水平方向）行进 100m 至索道口点 C 处，在点 C 处仰望山顶 A，测得仰角ACN=45求这座山的高度 （结果精确到 0.1m，
7、小明的身高忽略不计）（参考数据： 1.41， 1.73）22 （5 分）在平面直角坐标系 xOy 中，一次函数 y=x+b 的图象与 x 轴交于点 A（2，0） ，与反比例函数 y= 的图象交于点 B（3，n ） （1）求一次函数与反比例函数的表达式；（2）若点 P 为 x 轴上的点，且PAB 的面积是 2，则点 P 的坐标是 23 （5 分）如图，四边形 ABCD 是平行四边形，CEAD 于点 E，DFBA 交 BA 的延长线于点 F（1）求证：ADFDCE；（2）当 AF=2，AD=6，且点 E 恰为 AD 中点时，求 AB 的长24 （5 分）二次函数 y=x22mx+5m 的图象经过点
8、（1，2） （1）求二次函数图象的对称轴；（2）当4x1 时，求 y 的取值范围25 （6 分）如图，AC 是O 的直径，点 D 是O 上一点，O 的切线 CB 与 AD 的延长线交于点 B，点 F 是直径 AC 上一点，连接 DF 并延长交O 于点 E，连接 AE（1）求证：ABC=AED；（2）连接 BF，若 AD= ，AF=6 ，tanAED= ，求 BF 的长26 （7 分）在平面直角坐标系 xOy 中，抛物线 y=x2+mx+n 经过点 A（1，0）和B（0，3） （1）求抛物线的表达式；（2）抛物线与 x 轴的正半轴交于点 C，连接 BC设抛物线的顶点 P 关于直线 y=t 的对称
9、点为点 Q，若点 Q 落在OBC 的内部，求 t 的取值范围27 （7 分）在正方形 ABCD 中，点 P 在射线 AC 上，作点 P 关于直线 CD 的对称点 Q，作射线 BQ 交射线 DC 于点 E，连接 BP（1）当点 P 在线段 AC 上时，如图 1依题意补全图 1；若 EQ=BP，则PBE 的度数为 ，并证明；（2）当点 P 在线段 AC 的延长线上时，如图 2若 EQ=BP，正方形 ABCD 的边长为 1，请写出求 BE 长的思路 （可以不写出计算结果）28 （8 分）在平面直角坐标系 xOy 中，点 P 的坐标为（ x1，y 1） ，点 Q 的坐标为（x 2， y2） ，且 x1
10、x 2， y1y 2，若 PQ 为某个等腰三角形的腰，且该等腰三角形的底边与 x 轴平行，则称该等腰三角形为点 P，Q 的“相关等腰三角形”下图为点 P，Q的“相关等腰三角形”的示意图（1）已知点 A 的坐标为（0，1） ，点 B 的坐标为 ，则点 A，B 的“ 相关等腰三角形”的顶角为 ；（2）若点 C 的坐标为 ，点 D 在直线 y=4 上，且 C，D 的“相关等腰三角形”为等边三角形，求直线 CD 的表达式；（3）O 的半径为 ，点 N 在双曲线 y= 上若在O 上存在一点 M，使得点M、N 的“相关等腰三角形” 为直角三角形，直接写出点 N 的横坐标 xN 的取值范围2017-2018
11、 学年北京市石景山区九年级（上）期末数学试卷参考答案与试题解析一、选择题（本题共 16 分，每小题 2 分）第 1-8 题均有四个选项，符合题意的选项只有一个1如果 3x=4y（y0） ，那么下列比例式中正确的是（ ）A B C D【分析】根据比例的性质，可得答案【解答】解：A、由比例的性质，得 4x=3y 与 3x=4y 不一致，故 A 不符合题意；B、由比例的性质，得 xy=12 与 3x=4y 不一致，故 B 不符合题意；C、由比例的性质，得 4x=3y 与 3x=4y 不一致，故 C 不符合题意；D、由比例的性质，得 3x=4y 与 3x=4y 一致，故 D 符合题意；故选：D【点评】
12、本题考查了比例的性质，利用比例的性质是解题关键2在 RtABC 中，C=90， ，AC=2，则 tanA 的值为（ ）A B2 C D【分析】本题需先根据已知条件，得出 BC 的长，再根据正切公式即可求出答案【解答】解：C=90 ， AB= ，AC=2，BC=1，tanA= = 故选：A【点评】本题主要考查了锐角三角函数的定义，在解题时要根据在直角三角形中，正切等于对边比邻边这个公式计算是本题的关键3如图，AB 是O 的直径，点 C、D 在O 上若ACD=25，则BOD 的度数为（ ）A100 B120 C130 D150【分析】根据圆周角定理求出AOD 即可解决问题【解答】解：AOD=2AC
13、D ，ACD=25，AOD=50 ，BOD=180 AOD=18050=130，故选：C【点评】本题考查圆周角定理，邻补角的性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型4如图，在O 中，弦 AB 垂直平分半径 OC若 O 的半径为 4，则弦 AB 的长为（ ）A B C D【分析】连接 OA，由 AB 垂直平分 OC，求出 OD 的长，再利用垂径定理得到 D 为 AB的中点，在直角三角形 AOD 中，利用垂径定理求出 AD 的长，即可确定出 AB 的长【解答】解：连接 OA，由 AB 垂直平分 OC，得到 OD= OC=2，OCAB ，D 为 AB 的中点，则 AB=2AD=2
14、=2 =4 故选：B【点评】此题考查了垂径定理，以及勾股定理，根据题意作出辅助线，构造出直角三角形是解本题的关键5如果在二次函数的表达式 y=ax2+bx+c 中，a0，b0，c0，那么这个二次函数的图象可能是（ ）A BC D【分析】由 a0，b0， c0，推出 0，可知抛物线的图象开口向上，对称轴在y 轴的右边，交 y 轴于负半轴，由此即可判断【解答】解：a0，b 0，c0， 0，抛物线的图象开口向上，对称轴在 y 轴的右边，交 y 轴于负半轴，故选：C【点评】本题考查二次函数的图象，解题的关键是熟练掌握基本知识，灵活运用所学知识解决问题，属于中考常考题型6若二次函数 y=x2+2x+m
15、的图象与坐标轴有 3 个交点，则 m 的取值范围是（ ）Am 1 Bm1 Cm1 且 m0 Dm1 且 m0【分析】由抛物线与坐标轴有三个交点可得出：方程 x2+2x+m=0 有两个不相等的实数根，且 m0，利用根的判别式0 可求出 m 的取值范围，此题得解【解答】解：二次函数 y=x2+2x+m 的图象与坐标轴有 3 个交点，方程 x2+2x+m=0 有两个不相等的实数根，且 m0，=2 24m0，m1m1 且 m0故选：D【点评】本题考查了抛物线与 x 轴的交点以及根的判别式，利用根的判别式 0 找出关于 m 的一元一次不等式是解题的关键7如图，将函数 的图象沿 y 轴向上平移得到新函数图
16、象，其中原函数图象上的两点 A（1，m） 、B （4，n）平移后对应新函数图象上的点分别为点A、B若阴影部分的面积为 6，则新函数的表达式为（ ）A BC D【分析】先根据二次函数图象上点的坐标特征求出 A、B 两点的坐标，再过 A 作 ACx轴，交 BB 的延长线于点 C，则 C（4，1 ） ，AC=41=3，根据平移的性质以及曲线段 AB 扫过的面积为 6（图中的阴影部分） ，得出 AA=2，然后根据平移规律即可求解【解答】解：函数 y= （x 2） 2+1 的图象过点 A（1，m） ，B（4，n） ，m= （1 2） 2+1=1 ，n= （42） 2+1=2 ，A（1，1 ） ，B（4，
17、2 ） ，过 A 作 ACx 轴，交 BB 的延长线于点 C，则 C（ 4，1 ） ，AC=4 1=3，曲线段 AB 扫过的面积为 6（图中的阴影部分） ，ACAA=3AA=6，AA=2，即将函数 y= （x2） 2+1 的图象沿 y 轴向上平移 2 个单位长度得到一条新函数的图象，新图象的函数表达式是 y= （x 2） 2+3故选：B【点评】此题主要考查了二次函数图象与几何变换以及平行四边形面积求法等知识，根据已知得出 AA是解题关键8如图，点 M 为ABCD 的边 AB 上一动点，过点 M 作直线 l 垂直于 AB，且直线 l 与ABCD 的另一边交于点 N当点 M 从 AB 匀速运动时，
18、设点 M 的运动时间为 t，AMN 的面积为 S，能大致反映 S 与 t 函数关系的图象是（ ）A BC D【分析】当点 N 在 AD 上时，可得前半段函数图象为开口向上的抛物线的一部分；当点 N 在 DC 上时，MN 长度不变，可得后半段函数图象为一条线段【解答】解：设A= ，点 M 运动的速度为 a，则 AM=at，当点 N 在 AD 上时，MN=tanAM=tanat ，此时 S= attanat= tana2t2，前半段函数图象为开口向上的抛物线的一部分，当点 N 在 DC 上时，MN 长度不变，此时 S= atMN= aMNt，后半段函数图象为一条线段，故选：C【点评】本题主要考查了
19、动点问题的函数图象，用图象解决问题时，要理清图象的含义即会识图函数图象是典型的数形结合，图象应用信息广泛，通过看图获取信息，不仅可以解决生活中的实际问题，还可以提高分析问题、解决问题的能力二、填空题（本题共 16 分，每小题 2 分）9如果两个相似三角形的周长比为 2：3，那么这两个相似三角形的面积比为 4：9 【分析】根据相似三角形周长的比等于相似比，相似三角形面积的比等于相似比的平方解答【解答】解：因为两个相似三角形的周长比为 2：3，所以这两个相似三角形的相似比为 2：3，所以这两个相似三角形的面积比为 4：9；故答案为：4：9【点评】本题考查的是相似三角形的性质，相似三角形周长的比等于
20、相似比；相似三角形面积的比等于相似比的平方10如图，在ABC 中，点 D、E 分别在边 AB、AC 上若ADE=C， AB=6，AC=4 ，AD=2，则 EC= 1 【分析】只要证明ADEACB ，推出 = ，求出 AE 即可解决问题；【解答】解；A=A，ADE= C ，ADE ACB， = ， = ，AE=3，EC=ACAE=4 3=1，故答案为 1【点评】本题考查相似三角形的判定和性质，解题的关键是正确寻找相似三角形解决问题，属于中考常考题型11如图，扇形的圆心角AOB=60，半径为 3cm若点 C、D 是 的三等分点，则图中所有阴影部分的面积之和是 cm 2【分析】由题意可知 C、 D
21、是弧 AB 的三等分点，通过平移可把阴影部分都集中到一个小扇形中，可发现阴影部分正好是扇形 AOB 的 ，先求出扇形 AOB 的面积再求阴影部分的面积或者直接求圆心角是 20 度，半径是 3 的扇形的面积皆可【解答】解：S 扇形 OAB= ，S 阴影 = S 扇形 OAB= = 故答案为：【点评】此题考查扇形的面积问题，通过平移的知识把小块的阴影部分集中成一个规则的图形扇形，再求算扇形的面积即可利用平移或割补把不规则图形变成规则图形求面积是常用的方法12 “平改坡 ”是指在建筑结构许可条件下，将多层住宅的平屋顶改建成坡屋顶，并对外立面进行整修粉饰，达到改善住宅性能和建筑物外观视觉效果的房屋修缮
22、行为如图是某小区对楼顶进行“平改坡” 改造的示意图根据图中的数据，如果要使坡面 BC的坡度达到 1：1.2，那么立柱 AC 的长为 2.5 米【分析】由坡度的概念得出 = ，根据 AB=3 可得 AC 的长度【解答】解：根据题意知 = ，AB=3， = ，解得：AC=2.5，故答案为：2.5【点评】本题主要考查解直角三角形的应用坡度坡角问题，解题的关键是熟练掌握坡度的定义13如图，一次函数 y1=kx+b 的图象与反比例函数 y2= 的图象相交于点 A 和点B当 y1y 20 时，x 的取值范围是 2x 0.5 【分析】根据一次函数与反比例函数交点纵坐标，结合图象确定出所求 x 的范围即可【解
23、答】解：根据图象得：当 y1y 20 时，x 的取值范围是2x0.5，故答案为：2x0.5【点评】此题考查了反比例函数与一次函数的交点问题，利用了数形结合的思想，弄清数形结合思想是解本题的关键14如图，在 RtABC 中，C=90 ，AB=10，若以点 C 为圆心，CB 长为半径的圆恰好经过 AB 的中点 D，则 AC 的长等于 5 【分析】连接 CD，根据直角三角形斜边上的中线等于斜边的一半可得 AB=2CD，求出圆的半径的长，再利用勾股定理列式进行计算即可得解【解答】解：如图，C=90，点 D 为 AB 的中点，AB=2CD=10 ，CD=5，BC=CD=5，在 RtABC 中，AC= =
24、 =5 故答案为：5 【点评】本题考查了直角三角形斜边上的中线等于斜边的一半的性质，勾股定理的应用，求出圆的半径的长是解题的关键15如图，在平面直角坐标系 xOy 中，ABC 经过若干次图形的变化（平移、轴对称、旋转）得到DEF ，写出一种由 ABC 得到DEF 的过程： 向右平移 4 个单位，沿对称轴 BC 翻折，再绕点 C 逆时针旋转 90 【分析】根据对应点 C 与点 F 的位置，结合两三角形在网格结构中的位置解答【解答】解：ABC 向右平移 4 个单位，沿对称轴 BC 翻折，再绕点 C 逆时针旋转 90即可得到DEF ，所以，过程为：向右平移 4 个单位，沿对称轴 BC 翻折，再绕点
25、C 逆时针旋转 90故答案为：向右平移 4 个单位，沿对称轴 BC 翻折，再绕点 C 逆时针旋转 90【点评】本题考查了几何变换的类型，平移、旋转，准确识图是解题的关键16石景山区八角北路有一块三角形空地（如图 1）准备绿化，拟从点 A 出发，将ABC 分成面积相等的三个三角形，栽种三种不同的花草下面是小美的设计（如图 2） 作法：（1）作射线 BM；（2）在射线 BM 上顺次截取 BB1=B1B2=B2B3；（3）连接 B3C，分别过 B1、B 2 作 B1C1B 2C2B 3C，交 BC 于点 C1、C 2；（4）连接 AC1、AC 2则 请回答， 成立的理由是： 平行线分线段成比例定理
26、； 等底共高 【分析】根据平行线分线段成比例定理和等底共高求解可得【解答】解：由 BB1=B1B2=B2B3 且 B1C1B 2C2B 3C，依据平行线分线段成比例定理知BC1=C1C2=C2C，再由ABC 1， AC 1C2 与AC 2C 等底共高知 ，故答案为：平行线分线段成比例定理；等底共高【点评】本题主要考查作图应用与设计作图，解题的关键是掌握平行线分线段成比例定理和等底共高的两三角形面积关系三、解答题（本题共 68 分）解答应写出文字说明，演算步骤或证明过程.17 （5 分）计算：3tan30 cos245+ 2sin60【分析】根据特殊角三角函数值，可得答案【解答】解：原式=3 （
27、 ） 2+ 2= +2= 【点评】本题考查了特殊角三角函数值，熟记特殊角三角函数值是解题关键18 （5 分）用配方法求二次函数 y=x210x+3 的顶点坐标【分析】把解析式化为顶点式即可【解答】解：y=x 210x+3=（x5） 222，二次函数的顶点坐标为（5，22） 【点评】本题主要考查二次函数的性质，掌握二次函数的顶点式是解题的关键，即在y=a（x h） 2+k 中，顶点坐标为（ h，k） ，对称轴为 x=h19 （5 分）在 RtABC 中，C=90 ，A、B 、C 的对边分别为 a、b、c若a=2，sin ，求 b 和 c【分析】先根据 sinA= 知 c= =6，再根据勾股定理求
28、解可得【解答】解：如图，a=2，sin ，c= = =6，则 b= = =4 【点评】本题主要考查锐角三角函数的定义，解题的关键是掌握正弦函数的定义及勾股定理20 （5 分）小红和小丁玩纸牌游戏：如图是同一副扑克中的 4 张牌的正面，将它们正面朝下洗匀后放在桌上，小红先从中抽出一张，小丁从剩余的 3 张牌中也抽出一张比较两人抽出的牌面上的数字，数字大者获胜（1）请用树状图或列表法表示出两人抽牌可能出现的所有结果；（2）这个游戏公平吗？请说明理由【分析】 （1）根据题意画出树状图，即可解决问题；（2）根据树状图，利用概率公式即可求得小红获胜的概率，由概率相等，即可判定这个游戏公平；【解答】解：（
29、1）树状图如右：则小红获胜的概率： = ，小丁获胜的概率： = ，所以这个游戏比较公平【点评】本题考查的是用列表法与树状图法求事件的概率，解题的关键是学会正确画出树状图，判断游戏公平性就要计算每个事件的概率，概率相等就公平，否则就不公平用到的知识点为：概率=所求情况数与总情况数之比 21 （5 分）如图，小明想测量山的高度他在点 B 处仰望山顶 A，测得仰角ABN=30，再向山的方向（水平方向）行进 100m 至索道口点 C 处，在点 C 处仰望山顶 A，测得仰角ACN=45求这座山的高度 （结果精确到 0.1m，小明的身高忽略不计）（参考数据： 1.41， 1.73）【分析】作 AHBN 于
30、 H，设 AH=xm，根据正切的概念表示出 CH、BH，根据题意列出方程，解方程即可【解答】解：如图，作 AHBN 于 H，设 AH=xm，ACN=45，CH=AH=xm，tanB= ，BH= x，则 BHCH=BC，即 xx=100，解得 x=50（ +1） 答：这座山的高度为 50（ +1）m；【点评】本题考查的是解直角三角形的应用仰角俯角问题，正确作出辅助线、熟记锐角三角函数的概念是解题的关键22 （5 分）在平面直角坐标系 xOy 中，一次函数 y=x+b 的图象与 x 轴交于点 A（2，0） ，与反比例函数 y= 的图象交于点 B（3，n ） （1）求一次函数与反比例函数的表达式；（
31、2）若点 P 为 x 轴上的点，且PAB 的面积是 2，则点 P 的坐标是 （2，0）或（6，0） 【分析】 （1）利用待定系数法即可解决问题；（2）利用三角形的面积公式求出 PA 的长即可解决问题；【解答】解：（1）一次函数 y=x+b 的图象与 x 轴交于点 A（2，0） ，2+b=0，b=2，y=x2，当 x=3 时，y=1，B（3，1） ，代入 y= 中，得到 k=3，反比例函数的解析式为 y= （2）PAB 的面积是 2， PA1=2，PA=4，P（ 2，0）或（6，0） 【点评】本题考查一次函数的性质、反比例函数的性质等知识，解题的关键是灵活运用所学知识解决问题，属于中考常考题型2
32、3 （5 分）如图，四边形 ABCD 是平行四边形，CEAD 于点 E，DFBA 交 BA 的延长线于点 F（1）求证：ADFDCE；（2）当 AF=2，AD=6，且点 E 恰为 AD 中点时，求 AB 的长【分析】 （1）由平行四边形的性质知 CDAB，即 DAF= CDE，再由CEAD 、DFBA 知AFD= DEC=90 ，据此可得；（2）根据ADFDCE 知 = ，据此求得 DC=9，再根据平行四边形的性质可得答案【解答】解：（1）四边形 ABCD 是平行四边形，CDAB，DAF=CDE，又CEAD、DF BA ，AFD=DEC=90，ADFDCE ；（2）AD=6、且 E 为 AD
33、的中点，DE=3 ，ADFDCE ， = ，即 = ，解得：DC=9，四边形 ABCD 是平行四边形，AB=CD=9【点评】本题主要考查相似三角形的判定和性质，解题的关键是熟练掌握相似三角形的判定和性质及平行四边形的性质24 （5 分）二次函数 y=x22mx+5m 的图象经过点（1，2） （1）求二次函数图象的对称轴；（2）当4x1 时，求 y 的取值范围【分析】 （1）根据抛物线的对称性和待定系数法求解即可；（2）根据二次函数的性质可得【解答】解：（1）把点（1，2）代入 y=x22mx+5m 中，可得：12m+5m=2，解得：m=1，所以二次函数 y=x22mx+5m 的对称轴是 x=
34、，（2）y=x 2+2x5=（x+1） 26，当 x=1 时， y 取得最小值 6，由表可知当 x=4 时 y=3，当 x=1 时 y=6，当4x1 时，6y3【点评】本题考查了二次函数图象与性质及待定系数法求函数解析式，熟练掌握二次函数的图象与性质是解题的关键25 （6 分）如图，AC 是O 的直径，点 D 是O 上一点，O 的切线 CB 与 AD 的延长线交于点 B，点 F 是直径 AC 上一点，连接 DF 并延长交O 于点 E，连接 AE（1）求证：ABC=AED；（2）连接 BF，若 AD= ，AF=6 ，tanAED= ，求 BF 的长【分析】 （1）直接利用圆周角定理以及切线的性质
35、定理得出ACD=ABC ，进而得出答案；（2）首先得出 DC 的长，即可得出 FC 的长，再利用已知得出 BC 的长，结合勾股定理求出答案【解答】 （1）证明：连接 DC，AC 是O 的直径，BDC=90，ABC+BCD=90 ，O 的切线 CB 与 AD 的延长线交于点 B，BCA=90 ，ACD+BCD=90，ACD=ABC，ABC=AED；（2）解：连接 BF，在 RtADC 中，AD= ，tanAED= ，tanACD= = ，DC= AD= ，AC= =8，AF=6，CF=ACAF=86=2，ABC=AED，tanABC= = ， = ，解得：BD= ，故 BC=6，则 BF= =2
36、 【点评】此题主要考查了切线的性质与判定以及勾股定理等知识，正确得出ACD=ABC 是解题关键26 （7 分）在平面直角坐标系 xOy 中，抛物线 y=x2+mx+n 经过点 A（1，0）和B（0，3） （1）求抛物线的表达式；（2）抛物线与 x 轴的正半轴交于点 C，连接 BC设抛物线的顶点 P 关于直线 y=t 的对称点为点 Q，若点 Q 落在 OBC 的内部，求 t 的取值范围【分析】 （1）利用待定系数法即可解决问题；（2）分别求出点 Q 落在直线 BC 和 x 轴上时的 t 的值即可判断；【解答】解：（1）抛物线 y=x2+mx+n 经过点 A（1，0）和 B（0，3） ， ，解得
37、，抛物线的解析式为 y=x2+2x+3（2）如图，易知抛物线的顶点坐标为（1，4） 观察图象可知当点 P 关于直线 y=t 的对称点为点 Q 中直线 BC 上时，t=3 ，当点 P 关于直线 y=t 的对称点为点 Q 在 x 轴上时，t=2，满足条件的 t 的值为 2 t3【点评】本题考查二次函数的性质、待定系数法、轴对称等知识，解题的关键是熟练掌握基本知识，学会寻找特殊点解决问题，属于中考常考题型27 （7 分）在正方形 ABCD 中，点 P 在射线 AC 上，作点 P 关于直线 CD 的对称点 Q，作射线 BQ 交射线 DC 于点 E，连接 BP（1）当点 P 在线段 AC 上时，如图 1
38、依题意补全图 1；若 EQ=BP，则PBE 的度数为 45 ，并证明；（2）当点 P 在线段 AC 的延长线上时，如图 2若 EQ=BP，正方形 ABCD 的边长为 1，请写出求 BE 长的思路 （可以不写出计算结果）【分析】 （1）作点 P 关于直线 CD 的对称点 Q，作射线 BQ 交射线 DC 于点 E，连接BP； 依据题意得到 DP=EP，再根据四边形内角和求得BPE=90，根据 BP=EP，即可得到PBE=45；（2）连接 PD，PE，依据 CPDCPB，可得 DP=BP，1=2，根据 DP=EP，可得3= 1，进而得到PEB=45 ，3= 4=22.5，BCE 中，已知4=22.5
39、，BC=1，可求 BE 长【解答】解：（1）作图如下：如图，连接 PD，PE，易证 CPDCPB，DP=BP，CDP= CBP，P、Q 关于直线 CD 对称，EQ=EP，EQ=BP，DP=EP，CDP=DEP，CEP+DEP=180，CEP+CBP=180，BCD=90，BPE=90，BP=EP，PBE=45，故答案为：45 ；（2）思路：如图，连接 PD，PE，易证CPD CPB，DP=BP，1=2，P、Q 关于直线 CD 对称，EQ=EP，3=4，EQ=BP，DP=EP，3=1，3=2，5=BCE=90 ，BP=EP，PEB=45，3=4=22.5，在BCE 中，已知4=22.5，BC=1
40、 ，可求 BE 长【点评】此题是四边形综合题，主要考查了正方形的性质、轴对称的性质、全等三角形的判定与性质等知识的综合运用，解决本题的关键是熟记全等三角形的性质定理和判定定理28 （8 分）在平面直角坐标系 xOy 中，点 P 的坐标为（ x1，y 1） ，点 Q 的坐标为（x 2， y2） ，且 x1x 2， y1y 2，若 PQ 为某个等腰三角形的腰，且该等腰三角形的底边与 x 轴平行，则称该等腰三角形为点 P，Q 的“相关等腰三角形”下图为点 P，Q的“相关等腰三角形”的示意图（1）已知点 A 的坐标为（0，1） ，点 B 的坐标为 ，则点 A，B 的“ 相关等腰三角形” 的顶角为 120 ；（2）若点 C 的坐标为 ，点 D 在直线 y=4 上，且 C，D 的“相关等腰三角形”为等边三角形，求直线 CD 的表达式；（3）O 的半径为 ，点 N 在双曲线 y= 上若在O 上存在一点 M，使得点M、N 的“相关等腰三角形” 为直角三角形，直接写出点 N 的横坐标 xN 的取值范围【分析】 （1）画出图形求出BAO 的度数即可解决问题；（2）利用等边三角形的性质求出点 D 坐标即可解决问题；
