1、课题 29 图形的旋转A组 基础题组一、选择题1.(2018莱芜模拟)下列图形中,既是中心对称,又是轴对称的是( ) 2.(2018张家口模拟)如图,在正方形网格中有ABC,ABC 绕 O点按逆时针方向旋转 90后的图案应该是( )3.如图,AOB=90,B=30,AOB可以看做是由AOB 绕点 O顺时针方向旋转 度得到的.若点 A在 AB上,则旋转角 的大小可以是( )A.30 B.45 C.60 D.904.(2018廊坊安次模拟)如图,将正五边形 ABCDE绕其顶点 A沿逆时针方向旋转,若使点 B落在 AE边所在的直线上,则旋转的角度可以是( )A.72 B.54 C.45 D.365.
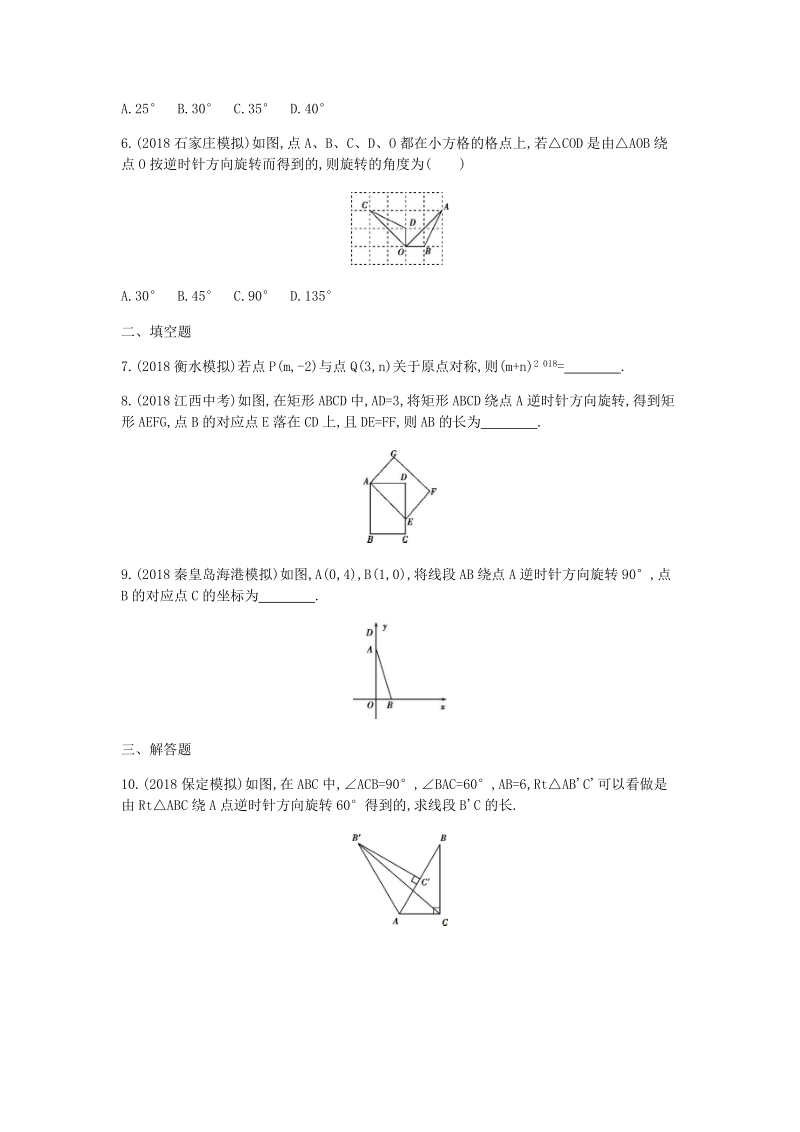
2、(2018沧州模拟)如图,ODC 是由OAB 绕点 O顺时针方向旋转 50后得到的图形,若点D恰好落在 AB上,且AOC 的度数为 130,则C 的度数是( )A.25 B.30 C.35 D.406.(2018石家庄模拟)如图,点 A、B、C、D、O 都在小方格的格点上,若COD 是由AOB 绕点 O按逆时针方向旋转而得到的,则旋转的角度为( )A.30 B.45 C.90 D.135二、填空题7.(2018衡水模拟)若点 P(m,-2)与点 Q(3,n)关于原点对称,则(m+n) 2 018= . 8.(2018江西中考)如图,在矩形 ABCD中,AD=3,将矩形 ABCD绕点 A逆时针方
3、向旋转,得到矩形 AEFG,点 B的对应点 E落在 CD上,且 DE=FF,则 AB的长为 . 9.(2018秦皇岛海港模拟)如图,A(0,4),B(1,0),将线段 AB绕点 A逆时针方向旋转 90,点B的对应点 C的坐标为 . 三、解答题10.(2018保定模拟)如图,在 ABC中,ACB=90,BAC=60,AB=6,RtABC可以看做是由 RtABC 绕 A点逆时针方向旋转 60得到的,求线段 BC的长.B组 提升题组一、选择题1.(2018黑龙江中考)下列图形中,既是轴对称图形又是中心对称图形的是( )2.(2018保定高阳模拟)如图,ABC 是等边三角形,四边形 BDEF是菱形,其
4、中线段 DF的长与DB的长相等,将菱形 BDEF绕点 B按顺时针方向旋转,甲、乙两位同学发现在此旋转过程中,有如下结论:线段 AF与线段 CD的长度总相等;直线 AF和直线 CD所夹的锐角的度数不变.那么,你认为( )A.都对 B.对,不对C.对,不对 D.都不对二、填空题3.(2018张家口模拟)如图,在ABC 中,C=90,AC=4,BC=3,将ABC 绕点 A逆时针方向旋转,使点 C落在线段 AB上的点 E处,点 B落在点 D处,则 B、D 两点间的距离为 . 4.(2018苏州中考)如图,在 RtABC 中,B=90,AB=2 ,BC= .将ABC 绕点 A按逆时针5 5方向旋转 90
5、得到ABC,连接 BC,则 sinACB= . 三、解答题5.(2017衡水冀州模拟)如图 1,在直角坐标系中,点 A的坐标为(0,12),经过原点的直线 l1与经过点 A的直线 l2相交于点 B(m,n).(1)若 m=9,n=3,求直线 l1和 l2的解析式;(2)将BAO 绕点 B顺时针方向旋转 180得到BFE,如图 2,连接 AE,OF.证明:四边形 OFEA是平行四边形.6.(2018河北模拟)如图 1,放置的一副三角尺,将含 45角的三角尺以其斜边上的中点 O为旋转中心,逆时针方向旋转 30得到如图 2,连接 OB、OD、AD.(1)求证:AOBAOD;(2)试判定四边形 ABO
6、D是什么四边形,并说明理由.答案精解精析A组 基础题组一、选择题1.C 2.A 3.C 4.A 在正五边形 ABCDE中,BAF= =72,使点 B落在 AE边所在的直线上,则沿逆3605时针方向旋转的角度是 72,故选 A.5.C AOC 的度数为 130,AOD=BOC=50,AOB=130-50=80,AOD 中,AO=DO,A= (180-50)=65,ABO 中,B=180-80-65=35,由旋转的性质可得,12C=B=35,故选 C.6.C 根据旋转方法,可知 OB与 OD是对应边,而 OB与 OD垂直,旋转角为 90,故选 C.二、填空题7.1 8.3 29. 答案 (4,5)
7、解析 过点 C作 CDy 轴于 D,如图所示,由旋转得 AB=AC,BAC=90,CAD+BAO=90.AOB=90,BAO+ABO=90,CAD=ABO,CDAAOB(AAS).AO=CD=4,OB=AD=1,OD=4+1=5,C(4,5),故答案为(4,5).三、解答题10. 解析 连接 BB,如图所示.根据旋转的性质,AB=AB,BAB=60.ABB是等边三角形,则 BB=AB=6,ABB=60.ACB=90,BAC=60,ABC=30,则BBC=90.在 RtABC 中,根据勾股定理,得 BC= = =3 .2-2 62-32 3在 RtBBC 中,根据勾股定理,得 BC= = =3
8、.2+2 62+(33)2 7B组 提升题组一、选择题1.C 2.A 连接 DF、AF、CD,如图,四边形 BDEF为菱形,BD=BF,而 DF=BD,BDF 为等边三角形,DBF=60.ABC 为等边三角形,BA=BC,ABC=60,ABF=CBD,ABF 绕点 B顺时针方向旋转 60可得到CBD,AF=CD,FAB=DCB,AHC=ABC=60,即直线 AF和直线 CD所夹的锐角的度数为 60.故选 A.二、填空题3. 答案 10解析 在ABC 中,C=90,AC=4,BC=3,AB=5,ABC 绕点 A逆时针方向旋转得到AED,DEA=C=90,AE=AC=4,DE=BC=3,BE=AB
9、-AE=5-4=1.连接 BD,在 RtBDE 中,由勾股定理可得 BD= = ,即 B、D 两点间的距离为 .2+2 10 104. 答案 45解析 在 RtABC 中,由勾股定理得 AC= =5.2+2过 C作 CMAB于 M,过 A作 ANCB于 N,如图所示.根据旋转方法,得AB=AB=2 , BAB=90,即CMA=MAB=B=90,CM=AB=2 ,AM=BC= ,BM=2 -5 5 5 5= .5 5在 RtBMC 中,由勾股定理得 BC= =5.2+2S ABC = BCAN= CMAB,即 5AN=2 2 ,解得 AN=4.12 12 5 5sin ACB= = ,故答案为
10、.45 45三、解答题5. 解析 (1)m=9,n=3,B(9,3).设直线 l1的解析式为 y=kx(k0),则 3=9k,解得 k= .13直线 l1的解析式为 y= x.13设直线 l2的解析式为 y=ax+b(a0),把点 A、B 代入,得 解得=12,9+=3, =-1,=12.直线 l2的解析式为 y=-x+12.(2)证明:将BAO 绕点 B顺时针方向旋转 180得BFE,AB=BF,BO=BE.四边形 OFEA是平行四边形.6. 解析 (1)证明:根据题意,得BAC=60,ABC=EDF=90,EF=AC,ODEF.O 为 AC、EF 的中点,OB= AC,OD= EF.12 12而 AC=EF,OB=OD=OA.BAO=60,AOB 是等边三角形.AOB=60,AB=OB=OA.DEF 绕斜边中点 O为旋转中心逆时针方向旋转 30得到图 2,AOE=30,AOD=90-30=60.AOD 为等边三角形.AOBAOD.(2)四边形 ABOD是菱形.理由如下:AOBAOD,AB=AD.AB=AD=OB=OD.四边形 ABOD 是菱形.
