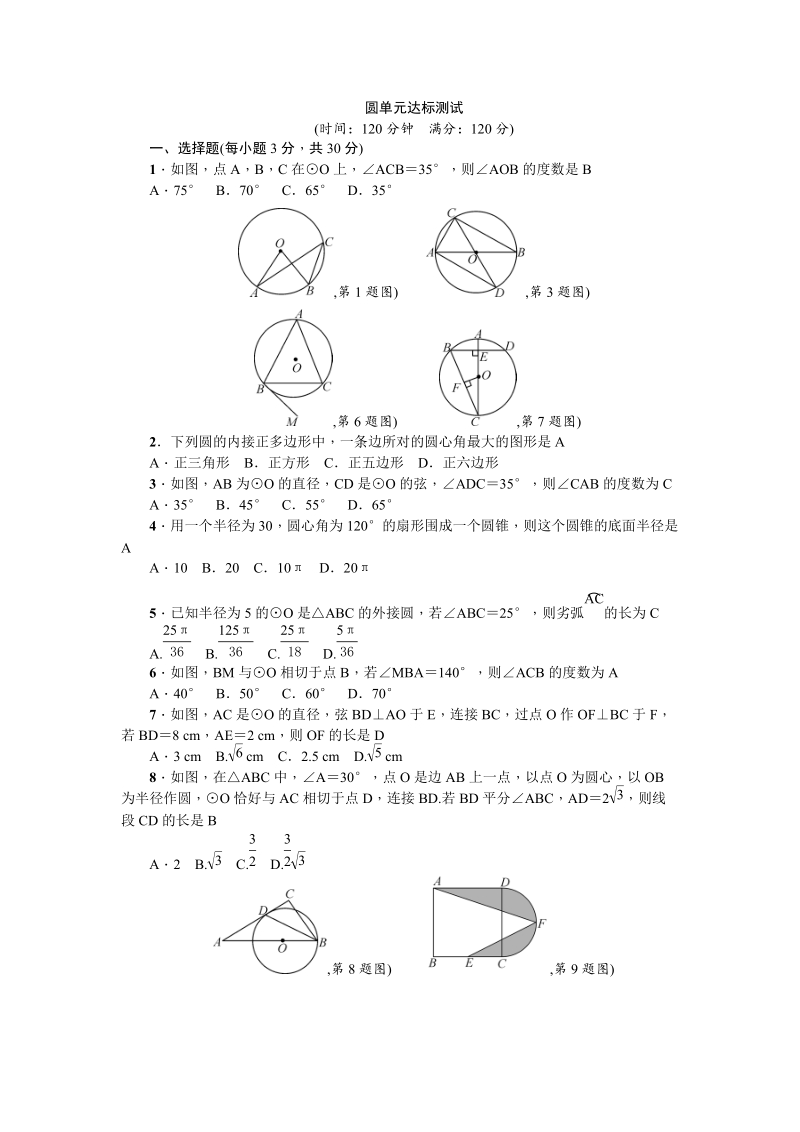
1、圆单元达标测试 (时间：120 分钟 满分：120 分)一、选择题(每小题 3 分，共 30 分)1如图，点 A，B，C 在O 上，ACB35，则AOB 的度数是 BA75 B70 C65 D35,第 1 题图) ,第 3 题图) ,第 6 题图) ,第 7 题图)2下列圆的内接正多边形中，一条边所对的圆心角最大的图形是 AA正三角形 B正方形 C正五边形 D正六边形3如图，AB 为O 的直径，CD 是O 的弦，ADC 35，则CAB 的度数为 CA35 B45 C55 D654用一个半径为 30，圆心角为 120的扇形围成一个圆锥，则这个圆锥的底面半径是AA10 B20 C10 D205已知
2、半径为 5 的O 是 ABC 的外接圆，若ABC25，则劣弧 的长为 CAC A. B. C. D.2536 12536 2518 5366如图，BM 与O 相切于点 B，若MBA 140，则 ACB 的度数为 AA40 B50 C60 D707如图，AC 是O 的直径，弦 BDAO 于 E，连接 BC，过点 O 作 OFBC 于 F，若 BD 8 cm，AE2 cm ，则 OF 的长是 DA3 cm B. cm C2.5 cm D. cm6 58如图，在ABC 中，A30，点 O 是边 AB 上一点 ，以点 O 为圆心，以 OB为半径作圆，O 恰好与 AC 相切于点 D，连接 BD.若 BD
3、 平分ABC，AD2 ，则线3段 CD 的长是 BA2 B. C. D.332 323,第 8 题图) ,第 9 题图) ,第 10 题图)9如图，在正方形 ABCD 中，AB12，点 E 为 BC 的中点 ，以 CD 为直径作半圆CFD，点 F 为半圆的中点，连接 AF，EF ，图中阴影部分的面积是 CA1836 B2418 C1818 D121810如图，在平面直角坐标系 xOy 中，A(4 ，0)，B(0，3)，C(4，3)，I 是ABC 的内心，将ABC 绕原点逆时针旋转 90后，I 的对应点 I的坐标为 AA(2，3) B(3，2) C(3 ，2) D(2，3)二、填空题(每小题 3
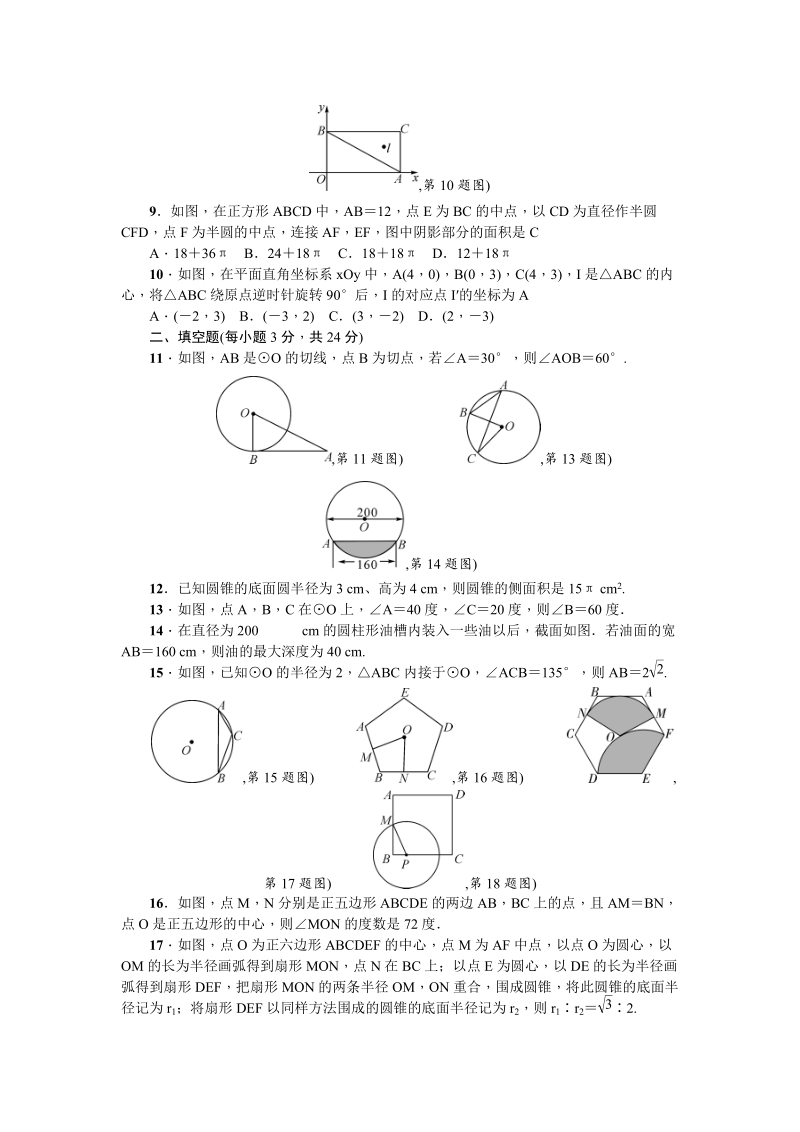
4、 分，共 24 分)11如图，AB 是O 的切线，点 B 为切点，若A30，则AOB60.,第 11 题图) ,第 13 题图) ,第 14 题图 )12已知圆锥的底面圆半径为 3 cm、高为 4 cm，则圆锥的侧面积是 15 cm 2.13如图，点 A，B，C 在 O 上，A40 度，C 20 度，则B60 度14在直径为 200 cm 的圆柱形油槽内装入一些油以后，截面如图若油面的宽AB160 cm，则油的最大深度为 40 cm.15如图，已知O 的半径为 2，ABC 内接于O ， ACB135，则 AB2 .2,第 15 题图) ,第 16 题图) ,第 17 题图) ,第 18 题图)
5、16如图，点 M，N 分别是正五边形 ABCDE 的两边 AB，BC 上的点，且 AMBN，点 O 是正五边形的中心，则 MON 的度数是 72 度17如图，点 O 为正六边形 ABCDEF 的中心，点 M 为 AF 中点，以点 O 为圆心，以OM 的长为半径画弧得到扇形 MON，点 N 在 BC 上；以点 E 为圆心，以 DE 的长为半径画弧得到扇形 DEF，把扇形 MON 的两条半径 OM，ON 重合，围成圆锥，将此圆锥的底面半径记为 r1；将扇形 DEF 以同样方法围成的圆锥的底面半径记为 r2，则 r1r 2 2.318如图，正方形 ABCD 的边长为 8，M 是 AB 的中点，P 是
6、 BC 边上的动点，连结PM， 以点 P 为圆心，PM 长为半径作P.当P 与正方形 ABCD 的边相切时，BP 的长为3 或 4 .3点拨：如图中，当P 与直线 CD 相切时，设 PCPMx.在 Rt PBM 中，PM 2BM 2PB 2，x 24 2(8x)2，x5，PC5，BP BCPC853.如图中 ，当P 与直线 AD 相切时设切点为 K，连接 PK，则 PKAD，四边形 PKDC 是矩形PMPKCD2BM，BM4，PM8，在 RtPBM 中，PB 4 .82 42 3三、解答题(共 66 分)19(8 分) 如图，已知 AB 是O 的弦，C 是 的中点，AB8，AC2 ，求O 半A
7、B 5径的长解：连接 OA，连接 OC 交 AB 于 D.设O 的半径为r. ， OC AB， ADDB AB4，在 RtACD 中，AC BC 12CD 2，在 RtADO 中，OA 2AD 2OD 2，r 2(r2) 216，解得AC2 AD2r5. O 的半径为 5.20(8 分) 如图，圆锥的侧面展开图是一个半圆，求母线 AB 与高 AO 的夹角参考公式：圆锥的侧面积 Srl，其中 r 为底面半径，l 为母线长解：设圆锥的母线长为 l，底面半径为 r，则 l 2r ，l2r，母线与高的夹角的正弦值 ，母线 AB 与高 AO 的夹角 30.rl 1221(8 分) 如图，已知 AB 是O
8、 的直径，C，D 是O 上的点，OCBD，交 AD 于点 E，连结 BC.(1)求证：AE ED；(2)若 AB10， CBD 36，求 的长AC 解：(1)证明：AB 是O 的直径，ADB 90.OC BD， AEOADB90，即 OCAD，AE ED.(2)OC AD， ， ABCCBD36，AC CD AOC 2ABC23672， 2.AC 72 51802210 分 已知 BC 是O 的直径 ，点 D 是 BC 延长线上一点 ，ABAD ，AE 是O的弦，AEC30.(1)求证：直线 AD 是O 的切线；(2)若 AEBC，垂足为 M， O 的半径为 4，求 AE 的长解：(1)证明：
9、AEC30，ABC30.AB AD ，DABC30，BAD 120，连接 OA，OAOB，OAB ABC30，OAD BADOAB90，OAAD.点 A 在O 上，直线 AD 是O 的切线(2)AEC30，AOC60.BCAE 于 M，AE 2AM，OMA90.在RtAOM 中， AMOAsinAOM4sin602 ，AE 2AM4 .3 323(10 分) 如图，C，D 是以 AB 为直径的O 上的点， ，弦 CD 交 AB 于点AC BC E.(1)当 PB 是O 的切线时，求证：PBDDAB；(2)求证：BC 2CE 2CEDE.证明：(1)AB 是O 的直径，ADB 90，即BADAB
10、D90.PB 是O 的切线，ABP90，即PBDABD90，BADPBD.(2) ，ABC BDC ，而ECB BCD， BCCB，BCE AC BC DCB，BC 2CECD，BC 2CE 2CECDCE 2CE(CDCE)CEDE.24(10 分) 如图，以 AB 为直径的O 外接于ABC ，过 A 点的切线 AP 与 BC 的延长线交于点 P， APB 的平分线分别交 AB，AC 于点 D，E，其中 AE，BD(AE BD)的长是一元二次方程 x25x60 的两个实数根(1)求证：PABDPBAE；(2)在线段 BC 上是否存在一点 M，使得四边形 ADME 是菱形？若存在，请给予证明，
11、并求其面积；若不存在，说明理由解：(1)证明：DP 平分APB，APEBPD.AP 与O 相切，BAP BACEAP 90.AB 是O 的直径，ACBBACB 90，EAP B，PAE PBD， ，PA BDPBAE.PAAE PBBD(2)过点 D 作 DFPB 于点 F，作 DGAC 于点 G，DP 平分APB， AD AP，DFPB， ADDF.EAPB ，APCBAC，易证DF AC， BDFBAC，由于 AE，BD(AE BD) 的长是 x25x60，解得AE2， BD3，由(1) 可知： ，cosAPC ，cosBDF cosAPC ， ，DF2，DPA2 PB3 PAPB 23
12、23 DFBD 23FAE， 四边形 ADFE 是平行四边形ADDF，四边形 ADFE 是菱形，此时点 F即为点 M.cosBAC cosAPC ，sinBAC ， ，DG ，在23 53 DGAD 53 253线段 BC 上存在一点 M，使得四边形 ADME 是菱形，其面积为 DGAE2 .253 45325(12 分) 如图，以 RtABC 的直角边 AB 为直径作O 交斜边 AC 于点 D，过圆心O 作 OEAC，交 BC 于点 E，连接 DE.(1)判断 DE 与 O 的位置关系并说明理由；(2)求证：2DE 2CDOE；(3)若 tanC ， DE ，求 AD 的长43 52解：(1
13、)DE 是 O 的切线，理由如下：连接 OD，BD，AB 是O 的直径，ADB BDC90.OE AC，OAOB，BECE，DEBE CE，DBEBDE.OBOD，OBD ODB，ODE OBE90.点 D 在O 上，DE 是O 的切线(2)BDCABC 90，C C，BCD ACB， ，BC 2CDAC ，由(1)知 DEBECE BC，4DE 2CDAC，由(1)BCAC CDBC 12知，OE 是ABC 是中位线， AC2OE，4DE 2CD2OE，2DE 2CDOE.(3)DE ， BC5，在 RtBCD 中，tanC ，设 CD3x，BD4x，根据52 43 BDCD勾股定理得，(3x) 2(4x) 225 ，x1( 舍)或 x1， BD4，CD3，由(2) 知，BC2CDAC， AC ，ADACCD 3 .BC2CD 253 253 163
