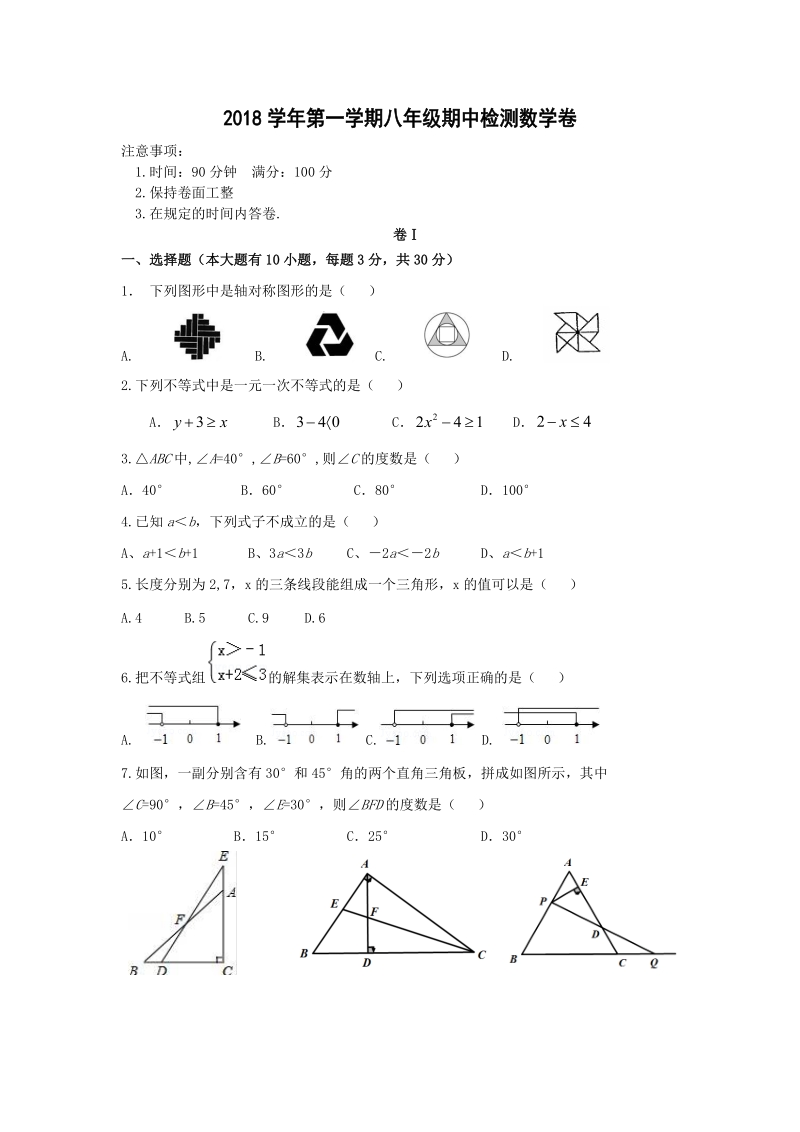
1、2018学年第一学期八年级期中检测数学卷注意事项：1.时间：90 分钟 满分：100 分2.保持卷面工整3.在规定的时间内答卷.卷一、选择题（本大题有 10 小题，每题 3 分，共 30 分）1 下列图形中是轴对称图形的是（ ）A. B. C. D. 2.下列不等式中是一元一次不等式的是（ ）A B C D3yx340241x24x3. ABC 中, A=40, B=60,则 C 的度数是（ ）A40 B60 C80 D1004.已知 a b，下列式子不成立的是（ ）A、 a+1 b+1 B、3 a3 b C、2 a2 b D、 a b+15.长度分别为 2,7，x 的三条线段能组成一个三角形
2、，x 的值可以是（ ）A.4 B.5 C.9 D.66.把不等式组 的解集表示在数轴上，下列选项正确的是（ ）A. B. C. D. 7.如图，一副分别含有 30和 45角的两个直角三角板，拼成如图所示，其中 C=90， B=45， E=30，则 BFD 的度数是（ ）A10 B15 C25 D30（第 7 题) (第 9 题) (第 10 题) 8.某商店的老板销售一种商品，他要以不低于进价 20%的价格才能出售，但为了获 得更多利润，他以高出进价 80%的价格标价若你想买下标价为 360 元的这种商品，最多降价（ ），商店老板才能出售A100 元 B80 元 C120 元 D160 元9.
3、如图，在ABC 中，BAC=90，AD 是边 BC 边上的高，CE 是ACB 的角平分线，交 AB于点 E，交 AD 于点 F，则 AE 与 AF 的大小关系是（ ）A. AEAF B.AEAF C.AE=AF D.不能确定10. 如图，过边长为 2 的等边 的边 AB 上一点 P，作 PEAC 于点 E，Q 为 BC 延长线上ABC一点，当 PA=CQ 时，连 PQ 交 AC 边于 D，则 DE 的长为（ ）11. A 1 B 1.5 C D 3 2卷二、填空题（本大题共有 8 小题，每小题 3 分，共 24 分）11.命题“两直线平行，同位角相等”的逆命题是_ _ _.12.用不等式表示：
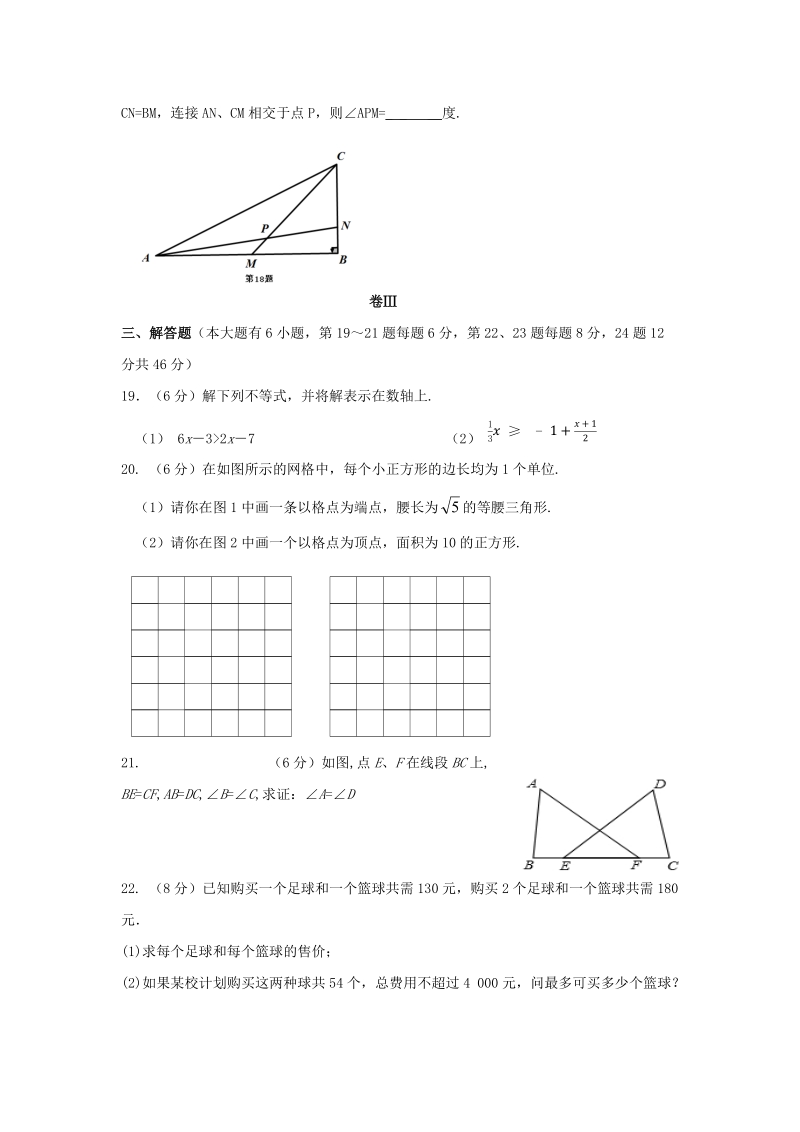
4、x 与 3 的差不小于 5，则这个不等式是_ _ _.13.已知等腰三角形的顶角为 70，则它的底角是_ _ _.14 等腰三角形两边长为 3 和 7，则这个等腰三角形的周长为_ _ _.15.如图， Rt ABC 中， ACB=90， CD 是高， AC=4cm， BC=3cm，则 CD=_ _ _16.如图，在 ABC 中， AD 是 ABC 的高线， AE 是 ABC 的角平分线。已知 B=40， C=70.则 DAE=_ _ _度17.已知，等腰ABC 中，底边 BC 上的高线与 AB 边的中垂线交于点 E，且 AE=5，BD=3，则SABC =_ _ _.18.如图，在ABC 中，B
5、=90，M 是 AB 上一点，使得 AM=BC，N 为 BC 上一点，使得CN=BM，连接 AN、CM 相交于点 P，则APM=_ _ _度.卷三、解答题（本大题有 6 小题，第 1921 题每题 6 分，第 22、23 题每题 8 分，24 题 12分共 46 分）19（6 分）解下列不等式，并将解表示在数轴上.（1） 6 x32 x7 （2） 13 -1+1220. （6 分）在如图所示的网格中，每个小正方形的边长均为 1 个单位.（1）请你在图 1 中画一条以格点为端点，腰长为 的等腰三角形.5（2）请你在图 2 中画一个以格点为顶点，面积为 10 的正方形.21. （6 分）如图,点
6、E、 F 在线段 BC 上,BE=CF,AB=DC, B= C,求证： A= D22. （8 分）已知购买一个足球和一个篮球共需 130 元，购买 2 个足球和一个篮球共需 180元(1)求每个足球和每个篮球的售价；(2)如果某校计划购买这两种球共 54 个，总费用不超过 4 000 元，问最多可买多少个篮球？23. （8 分）如图，等边 ABC 中， AO 是 BAC 的角平分线， D为 AO 上一点，以 CD 为一边且在 CD 下方作等边 CDE，连接BE（1）求证： ACD BCE（2）求 EBC 的度数？（3）延长 BE 至 Q， P 为 BQ 上一点，连接 CP、 CQ 使CP=CQ
7、=10，若 BC=12 时，求 PQ 的长24. （12 分）如图，ABC 和ACD 都是边长为 4 厘米的等边三角形，两个动点 P，Q 同时从点 A 出发，点 P 以 1 厘米/秒的速度沿 ACB 的方向运动，点 Q 以 2 厘米/秒的速度沿ABCD 的方向运动，当点 Q 运动到 D 点时，P、Q 两点同时停止运动.设 P、Q 运动的时间为 t 秒.（1）当 t=2 时，PQ=；（2）求点 P、Q 从出发到相遇所用的时间；（3）当 t 取何值时，APQ 是等边三角形.请说明理由.（4）当 P 在线段 AC 上运动时，是否存在 t使APQ 是直角三角形？若存在请直接写出t 的值或 t 的取值范
8、围，若不存在，请说明理由.QD CA BP八年级五校期中数学试卷答案一、 选择题题号 1 2 3 4 5 6 7 8 9 10答案 C D C C D D B C C A二、 填空题11. 同位角相等，两直线平行 12. x-35 13. 55 14. 17 15. 16. 15 17. 27 18. 45 125三、解答题19. （1）4x-4 （2）2x-6+3（x+1）x-1 -x-3 x3 注：每小题 3 分，不等式计算 2 分，数轴 1 分20. 每小题 3 分21.证明：BE=CF，BE+EF=CF+EF，BF=CE（2 分）在ABF 和DCE 中AB=DC（已知）B=C （已知）
9、BF=CE(已证)ABFDCE （SAS）（3 分）A=D(全等三角形对应角相等) （1 分）22. （1）解：设足球单价 x 元，篮球单价 y 元，由题意得x+y=1302x+y=180（2 分）解得 x=50y=80 答：足球单价 50 元，篮球单价 80 元。（2 分）（2）设购买篮球 x 个，则购买足球（54-x）个，可得80x+50（54-x）4000，（2 分）解得 x ，篮球最多 43 个（2 分）1303答:最多可买 43 个篮球.23. （1）证明：在等边ABC 和等边CDE 中，AC=BC，DC=CE，ACB=DCE=60ACD=BCE（1 分）在ACD 和BCE 中AC=
10、BCACD=BCEDC=CEACDBCE（SAS）（ 2 分）（2）由（1）得ACDBCE，EBC=DACAD 是BAC 的角平分线，DAC=30EBC=30（2 分）（3）过点 P 作 CFBQ 于点 FEBC=30，BC=12，CF=6（30所对的直角边是斜边的一半）（1 分）又CP=10，RtPCF 中，据勾股定理得，PF=8 （1 分）又CP=CQ，CF 是 PQ 边上的中线（三线合一），PQ=2PF=16（1 分）24.（不同解法可酌情给分） （1） ；（2 分）23（2）由题意得，点 P 从 A CB，点 Q 从 ABC D，当 P、Q 相遇即 SP+SQ=CABC，t+2t=12，t=4. （3 分）（3）当 0t4，不存在等边APQ 的情况（1 分）当 4t6 时，如图，若APQ 是等边三角形，此时点 P 在 BC 上，Q 在 CD 上，且ADQACP，则 CP=DQ，CP=t-4，DQ=12-2t，则 t= . （3 分）163（4）P 在线段 AC 上运动时，存在 t 使APQ 一直是直角三角形，t 的范围是0t4. PBDACQFQEOCBADP（3 分）
