1、2018 年湖北省随州市广水市 XX 中学中考数学模拟试卷（二）一选择题（共 10 小题，满分 21 分）1下列四个数中，正整数是（ ）A 2 B1 C0 D12下列数学符号中，属于中心对称图形的是（ ）A B C D3我国是一个严重缺水的国家，大家应倍加珍惜水资源，节约用水据测试，拧不紧的水龙头每秒钟会 滴下 2 滴水，每滴水约 0.05 毫升若每天用水时间按2 小时计算，那么一天中的另外 22 小时水龙头都在不断的滴水请计算，一个拧不紧的水龙头，一个月（按 30 天计算）浪费水（ ）A23760 毫升 B2.37610 5 毫升C 23.8104 毫升 D237.610 3 毫升4 （3
2、分）如图，在ABC 中，AB=AC，AD 平分BAC，DEAB，DFAC ，E、F 为垂足，则下列四个结论：（1）DEF= DFE；（2）AE=AF；（3）AD 平分EDF；（4）EF 垂直平分 AD其中正确的有（ ）A1 个 B2 个 C3 个 D4 个5 （3 分）若 5x=125y，3 y=9z，则 x：y：z 等于（ ）A1 ：2 ：3 B3：2：1 C1：3：6 D6：2：16 （3 分）下列说法正确的是（ ）A “明天降雨的概率是 60%”表示明天有 60%的时间都在降雨B “抛一枚硬币正面朝上的概率为 ”表示每抛 2 次就有一次正面朝上C “彩票中奖的概率为 1%”表示买 100
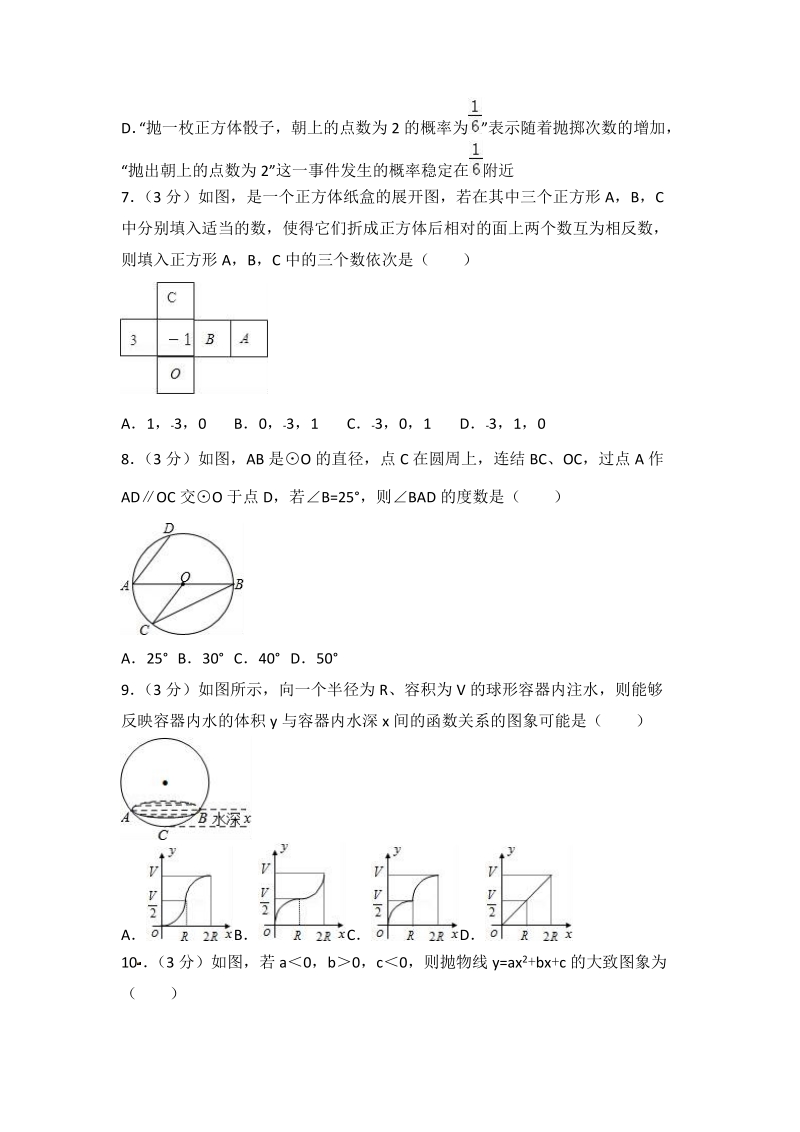
3、 张彩票肯定会中奖D “抛一枚正方体骰子，朝上的点数为 2 的概率为 ”表示随着抛掷次数的增加，“抛出朝上的点数为 2”这一事件发生的概率稳定在 附近7 （3 分）如图，是一个正方体纸盒的展开图，若在其中三个正方形 A，B，C中分别填入适当的数，使得它们折成正方体后相对的面上两个数互为相反数，则填入正方形 A，B，C 中的三个数依次是（ ）A1 ， 3，0 B0，3，1 C 3，0，1 D3，1，08 （3 分）如图，AB 是 O 的直径，点 C 在圆周上，连结 BC、OC，过点 A 作ADOC 交O 于点 D，若B=25，则BAD 的度数是（ ）A25 B30 C40 D509 （3 分）如
4、图所示，向一个半径为 R、容积为 V 的球形容器内注水，则能够反映容器内水的体积 y 与容器内水深 x 间的函数关系的图象可能是（ ）A B C D 来源:Zxxk.Com10 （3 分）如图，若 a0，b 0，c 0，则抛物线 y=ax2+bx+c 的大致图象为（ ）A B C D二填空题（共 6 小题，满分 18 分，每小题 3 分）11 （3 分）分解因式（xy1） 2（x+y2xy） （2 xy）= 12 （3 分）已知关于 x 的一元二次方程 x24x+k=0 有两个不相等的实数根，且该方程与 x2+mx1=0 有一个相同的根当 k 为符合条件的最大整数时， m 的值为 13 （3
5、分）如图，在ABC 中，BC 边上的垂直平分线 DE 交边 BC 于点 D，交边AB 于点 E若EDC 的周长为 24，ABC 与四边形 AEDC 的周长之差为 12，则线段 DE 的长为 14 （3 分）投掷一枚普通的正方体骰子，则掷得“6”概率是 ，其含义是 15 （3 分）用等分圆周的方 法，在半径为 1 的图中画出如图所示图形，则图中阴影部分面积为 16 （3 分）如图，抛物线 y=x2 在第一象限内经过的整数点（横坐标、纵坐标都为整数的点）依次为 A1，A 2，A 3An，将抛物线 y=x2 沿直线 L：y=x 向上平移，得一系列抛物线，且满足下列条件：抛物线的顶点 M1，M 2，M
6、 3，M n，都在直线 L：y=x 上；抛物线依次经过点 A1，A 2，A 3An，则顶点 M2014 的坐标为（ ， ） 三解答题（共 2 小题）17已知 Rt ABC 中，C=90 ，a+b=2 +2 ，c=4，求锐角 A 的度数18到 高中时，我们将学习虚数 i， （i 叫虚数单位） 规定 i2=1，如2=2（1）=（ ） 2i2=（i） 2，那么 x2=2 的根就是：x1= i，x 2= i试求方程 x2+2x+3=0 的根四解答题（共 4 小题）19如图，ABCD 中，AB=2，以点 A 为圆心，AB 为半径的圆交边 BC 于点 E，连接 DE，AC，AE（1）求证：AED DCA（
7、2）若 DE 平分 ADC 且与 A 相切于点 E，求图中阴影部分（扇形）的面积20某电视台的一档娱乐性节目中，在游戏 PK 环节，为了随机分选游戏双方的组 员，主持人设计了以下游戏：用不透明的白布包住三根颜色长短相同的细绳AA1、BB 1、CC 1，只露出它们的头和尾（如图所示） ，由甲、乙两位嘉宾分别从白布两端各选一根细绳，并拉出，若两人选中同一根细绳，则两人同队，否则互为反方队员（1）若甲嘉宾从中任意选择一根细绳拉出，求他恰好抽出细绳 AA1 的概率；（2）请用画树状图法或列表法，求甲、乙两位嘉宾能分为同队的概率21如图所示，小王在校园上的 A 处正面观测一座教学楼墙上的大型标牌，测得标
8、牌下端 D 处的仰角为 30，然后他正对大楼方向前进 5m 到达 B 处，又测得该标牌上端 C 处的仰角为 45若该楼高为 16.65m，小王的眼睛离地面1.65m，大型标牌的上端与楼房的顶端平齐求此标牌上端与下端之间的距离（1.732，结果精确到 0.1m） 22如图，某日的钱塘江观潮信息如图：按上述信息，小红将“ 交叉潮” 形成后潮头与乙地之间的距离 s（千米）与时间t（分钟）的函数关系用图 3 表示，其中：“11 ：40 时甲地 交叉潮的潮头离乙地12 千米”记为点 A（0，12） ，点 B 坐标为（m，0） ，曲线 BC 可用二次函数 s=t2+bt+c（ b，c 是常数）刻画（1）求
9、 m 的值，并求出潮头从甲地到乙地的速度；（2）11 ：59 时，小红骑单车从乙地出发，沿江边公路以 0.48 千米/分的速度往甲地方向去看潮，问她几分钟后与潮头相遇？（3）相遇后，小红立即调转车头，沿江边公路按潮头速度与潮头并行，但潮头过乙地后均匀加速，而单车最高速度为 0.48 千米/分，小红逐渐落后问小红与潮头相遇到落后潮头 1.8 千米共需多长时间？（潮水加速阶段速度v=v0+ （t 30） ，v 0 是加速前的速度） 五解答题（共 2 小题）23我们定义：如图 1，在ABC 看，把 AB 点 A 顺时针旋转 （0 180 ）得到 AB，把 AC 绕点 A 逆时针旋转 得到 AC，连接
10、 BC当 +=180时，我们称ABC是 ABC 的“ 旋补三角形 ”，ABC边 BC上的中线 AD 叫做ABC 的“旋补中线”，点 A 叫做“旋补中心”特例感知：（1）在图 2，图 3 中，ABC是ABC 的“旋补三角形”，AD 是ABC 的“旋补中线”如图 2，当ABC 为等边三角形时， AD 与 BC 的数量关系为 AD= BC；如图 3，当BAC=90 ， BC=8 时，则 AD 长为 猜想论证：（2）在图 1 中，当ABC 为任意三角形时，猜想 AD 与 BC 的数量关系，并给予证明24已知平面直角坐标系中两定点 A（ 1，0） 、B（4，0） ，抛物线y=ax2+bx2（ a0）过点
11、 A，B ，顶点为 C，点 P（m ，n ） （n0）为抛物线上一点（1）求抛物线的解析式和顶点 C 的坐标；（2）当APB 为钝角时，求 m 的取值范围；（3）若 m ，当APB 为直角时，将该抛物线向左或向右平移 t（0t ）个单位，点 C、P 平移后对应的点分别记为 C、P，是否存在 t，使得首位依次连接 A、B、P、C所构成的多边形的周长最短？若存在，求 t 的值并说明抛物线平移的方向；若不存在，请说明理由2018 年湖北省随州市广水市 XX 中学中考数学模拟试卷（二）参考答案与试题解析一选择题（共 10 小题，满分 21 分）1【解答】解：A、2 是负整数，故选项错误；B、1 是负整
12、数，故选项错误；C、 0 是非正整数，故选项错误；D、1 是正整数，故选项正确故选：D2【解答】解：A、不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项正确；C、不是中心对称图形，故本选项错误；D、不是中心对称图形，故本选项错误故选：B3【解答】解：20.05（226060）30=0.1 7920030=2.376105 毫升故选：B4【解答】解：AB=AC，AD 平分BAC ，DEAB ， DFACABC 是等腰三角形，ADBC，BD=CD，BED=DFC=90DE=DFAD 垂直平分 EF（4）错误；又AD 所在直线是 ABC 的对称轴，（1）DEF=DFE ；（2 ）AE=A
13、F；（3）AD 平分 EDF故选：C5【解答】解：5 x=（5 3） y=53y，3 y=（3 2） z=32z，x=3y，y=2z，即 x=3y=6z；设 z=k，则 y=2k，x=6k ；（k0）x ：y：z= 6k：2k：k=6：2：1故选：D6【解答】解：A、 “明天降雨的概率是 60%”表示明天下雨的可能性较大，故 A 不符合题意；B、 “抛一枚硬币正面朝上的概率为 ”表示每次抛正面朝上的概率都是 ，故 B 不符合题意；C、 “彩票中奖的概率为 1%”表示买 100 张彩票有可能中奖故 C 不符合题意；D、 “抛一枚正方体骰子，朝上的点数为 2 的概率为 ”表示随着抛掷次数的增加，“
14、抛出朝上的点数为 2”这一事件发生的概率稳定在 附近，故 D 符合题意；故选：D7【解答】解：根据以上分析：填入正方形 A，B ，C 中的三个数依次是1， 3，0 故选：A8【解答】解：OB=OC，B= C，B=25，C=25，AOC=2B，AOC=50，ADOC，BAD=AOC=50 ，故选：D9【解答】解：根据球形容器形状可知，函数 y 的变化趋势呈现出，当 0xR时，y 增量越来越大，当 Rx2R 时，y 增量越来越小，曲线上的点的切线斜率先是逐渐变大，后又逐渐变小，故 y 关于 x 的函数图象是先凹后凸故选：A10【解答】解：a0，抛物线的开口方向向下，故第三个选项错误；c0，抛物线与
15、 y 轴的交点为在 y 轴的负半轴上，故第一个选项错误；a 0 、b 0，对称轴为 x= 0，对称轴在 y 轴右侧，故第四个选项错误故选：B二填空题（共 6 小题，满分 18 分，每小题 3 分）11【解答】解：令 x+y=a，xy=b，则（xy 1） 2（x+y2xy） （2 xy）=（ b1） 2（a2b） （2a ）=b22b+1+a22a2ab+4 b=（ a22ab+b2）+2b2a +1=（ ba） 2+2（ba）+1=（ ba+1） 2；即原式=（xyxy+1） 2=x（y 1）（y1） 2=（y1） （x1） 2=（y1） 2（x1） 2来源:学_科_网 故答案为：（y1） 2
16、（x1） 212【解答】解：关于 x 的一元二次方程 x24x+k=0 有两个不相等的实数根，=164k 0，解得 k4，k 的最大整数值是 3，即 k=3；x 24x+3=0，即（ x1） （x 3）=0 ，解得，x=1 或 x=3；当与 x2+mx1=0 相同的根是 x=1 时，1+m 1=0，解得 m=0；当与 x2+mx1=0 相同的根是 x=3 时，9+3m1=0，解得 m= ；综合知，符合条件的 m 的值为 0 或 故答案为：0 或 13【解答】解：DE 是 BC 边上的垂直平分线，BE=CE EDC 的周长为 24，ED+DC +EC=24，ABC 与四边形 AEDC 的周长之差
17、为 12，（AB+AC+BC）（AE+ED+DC +AC）= （AB +AC+BC）（AE+DC +AC）DE=12，BE +BDDE=12，BE=CE ，BD=DC，得，DE=6故答案为：614【解答】解：掷一次 骰子有 6 种情况，即 1，2 ，3，4，5，6 朝上；则朝上的一面为 6 点的概率是 其含义是：掷一次骰子有 6 种情况，则朝上的一面为 6 点的可能占 故答案为： ，掷一次骰子有 6 种情况，则朝上的一面为 6 点的可能占 15【解答】解：如图，设 的中点为 P，连接 OA，OP ，AP ，OAP 的面积是： 12= ，扇形 OAP 的面积是：S 扇形 = ，AP 直线和 AP
18、 弧面积：S 弓形 = ，阴影面积：32S 弓形 = 故答案为： 16【解答】解：M 1（a 1，a 1）是抛物线 y1=（xa 1） 2+a1 的顶点，抛物线 y=x2 与抛物线 y1=（x a1） 2+a1 相交于 A1，得 x2=（xa 1） 2+a1，即 2a1x=a12+a 1，x= （a 1+1） x 为整数点a 1=1，M1（ 1，1） ；M2（ a2，a 2）是抛物线 y2=（xa 2） 2+a2=x22a2x+a22+a2 顶点，抛物线 y=x2 与 y2 相交于 A2，x2=x22a2x+a22+a2，2a 2x=a22+a2，x= （a 2+1） x 为整数点，a 2=3
19、，M2（ 3，3） ，M3（ a3，a 3）是抛物线 y2=（xa 3） 2+a3=x22a3x+a32+a3 顶点，抛物线 y=x2 与 y3 相交于 A3，x2=x22a3x+a32+a3，2a 3x=a32+a3，x= （a 3+1） x 为整数点a 3=5，M3（ 5，5） ，点 M2014，两坐标为： 201421=4027，M 2014（4027，4027 ） ，故答案为：（4027，4027）三解答题（共 2 小题）17【解答】解：将 a+b=2+2 两边平方，整理得 ab=4 ，又因为 a+b=2+2 ，构造一元二次方程得 x2（2+2 ）x +4 =0，解得 x1=2，x 2
20、=2则（1）sinA= = 时，锐角 A 的度数是 30，（2）sinA= = 时，锐角 A 的度数是 60，所以A=30或A=6018【解答】解：x 2+2x+3=0，x 2+2x+1=2，（x+1） 2=2，x+1= i，解得 x=1 i，所以 x1=1+ i，x 2=1 i四解答题（共 4 小题）19【解答】解：（1）证明：四边形 ABCD 是平行四边形，AB=CD，ADBC，四边形 AECD 是梯形，AB=AE，AE=CD，四边形 AECD 是等腰梯形，AC=DE，在AED 和 DCA 中，AED DCA（SSS） ；（2）解：DE 平分ADC，ADC=2 ADE，四边形 AECD 是
21、等腰梯形，DAE= ADC=2ADE，DE 与A 相切于点 E，AE DE ，即AED=90 ，ADE=30 ，DAE=60 ，DCE=AEC=180DAE=120 ，四边形 ABCD 是平行四边形，BAD=DCE=120，BAE=BAD EAD=60 ，S 阴影 = 22= 20【解答】解：（1）共有三根细绳，且抽出每根细绳的可能性相同，甲嘉宾从中任意选择一根细绳拉出，恰好抽出细绳 AA1 的概率是= ；（2）画树状图：共有 9 种等可能的结果数，其中甲、乙两位嘉宾能分为同队的结果数为 3 种情况，则甲、乙两位嘉宾能分为同队的概率是 = 21【解答】解：设 AB，CD 的延长线相交于点 E，
22、CBE=45 ，CEAE，CE=BE ，CE=16.651.65=15，BE=15，而 AE=AB+BE=20DAE=30 ， 11.54，CD=CEDE=15 11.543.5 （m ） ，答：大型标牌上端与下端之间的距离约为 3.5m22【解答】解：（1）由题意可知：m=30；B（30，0 ） ，潮头从甲地到乙地的速度为： 千米/ 分钟；（2）潮头的速度为 0.4 千米/ 分钟，到 11：59 时，潮头已前进 190.4=7.6 千米，设小红出发 x 分钟与潮头相遇，0.4x+0.48x=127.6，x=5小红 5 分钟与潮头相遇，（3）把 B（30，0） ，C （ 55，15 ）代入 s
23、= t2+bt+c，解得：b= ，c= ，s= t2 v 0=0.4，v= （t30）+ ，当潮头的速度达到单车最高速度 0.48 千米/ 分钟，此时 v=0.48，0.48= （ t30）+ ，t=35，当 t=35 时，s= t2 = ，从 t=35 分（12 ：15 时）开始，潮头快于小红速度奔向丙地，小红逐渐落后，但小红仍以 0.48 千米/分的速度匀速追赶潮头设她离乙地的距离为 s1，则 s1 与时间 t 的函数关系式为 s1=0.48t+h（t35） ，当 t=35 时，s 1=s= ，代入可得：h= ，s 1= 最后潮头与小红相距 1.8 千米时，即 ss1=1.8， t2 +
24、=1.8来源:学.科. 网 Z.X.X.K解得：t=50 或 t=20（不符合题意，舍去） ，t=50，小红与潮头相遇后，按潮头速度与潮头并行到达乙地用时 6 分钟，共需要时间为 6+5030=26 分钟，小红与潮头相遇到潮头离她 1.8 千米外共需要 26 分钟，来源:Zxxk.Com五解答题（共 2 小题）23【解答】解：（1）如图 2，当ABC 为等边三角形时， AD 与 BC 的数量关系为 AD= BC；理由：ABC 是等边三角形，AB=BC=AC=AB=AC，DB=DC，ADBC，BAC=60 ，BAC +BAC=180，BAC=120，B=C=30，AD= AB= BC，故答案为
25、如图 3，当BAC=90 ， BC=8 时，则 AD 长为 4理由：BAC=90 ，BAC +BAC=180 ，BAC= BAC=90，AB=AB，AC=AC，BACBAC，BC=BC，BD=DC，AD= BC= BC=4，故答案为 4（2）猜想 证明：如图，延长 AD 至点 Q，则DQB DAC，QB=AC，QB AC，QBA+BAC=180，BAC+BAC=180 ，QBA=BAC，又由题意得到 QB=AC=AC，AB=AB ，AQBBCA，AQ=BC=2AD，即 24【解答】解：（1）抛物线 y=ax2+bx2（a0）过点 A，B， ，解得： ，抛物线的解析式为：y= x2 x2；y=
26、x2 x2= （x ） 2 ，C （ ， ） （2）如图 1，以 AB 为直径作圆 M，则抛物线在圆内的部分，能使 APB 为钝角，M（ ，0） ，M 的半径= P是抛物线与 y 轴的交点，OP=2 ，MP= = ，P在M 上，P的对称点（3，2） ，当1m0 或 3m4 时，APB 为钝角（3）方法一：存在；抛物线向左或向右平移，因为 AB、 PC是定值，所以 A、B、P、C所构成的多边形的周长最短，只要 AC+BP最小；第一种情况：抛物线向右平移，AC+BPAC+BP，第二种情况：向左平移，如图 2 所示，由（2）可知 P（3， 2） ，又C （ ， ）C（ t， ） ，P（3 t，2）
27、，AB=5，P（ 2t，2） ，要使 AC+BP最短，只要 AC+AP最短即可，点 C关于 x 轴的对称点 C（ t， ） ，设直线 PC的解析式为：y=kx+b，解得直线 y= x+ t+ ，当 P、 A、C在一条直线上时，周长最小， + t+ =0t= 故将抛物线向左平移 个单位连接 A、B、P、C所构成的多边形的周长最短方法二：AB、PC是定值，A、B、P、C所构成的四边形的周长最短，只需 AC+BP最小，若抛物线向左平移，设平移 t 个单位，C（ t， ） ，P（2t，2） ，四边形 PABP为平行四边形，AP=BP ，AC+BP最短，即 AC+AP最短，C关于 x 轴的对称点为 C（ t， ） ，C，A，P三点共线时，AC+AP最短，KAC=KAP， ，t= 若抛物线向右平移，同理可得 t= ，将抛物线向左平移 个单位时，A 、B、P、C所构成的多边形周长最短
