1、重庆市江北区 20172018 学年度下期九年级中考模拟考试数 学 试 题（考试时间：120 分钟，满分：150 分）注意事项：1选择题用 2B 铅笔,解答题的答案用 0.5 毫米的黑色签字笔书写在答题卷上,不得在试卷上直接作答;2答题前,请认真阅读答题卷上的注意事项,并按要求填写内容和答题;3作图（包括作辅助线）,请一律用黑色签字笔完成;4考试结束,由监考人员将试题和答题卷一并收回. 一、选择题：（本大题 12 个小题，每小题 4 分，共 48 分）在每个小题的下面，都给出了代号为 A、B、C、D 的四个答案，其中只有一个是正确的，请将答题卡上题号右侧正确答案所对应的方框涂黑12 的倒数是（
2、 ）A2 B1 C1 D 122 下列图形中，是中心对称图形的是（ ）A B C D3计算 的结果是（ ）32(5)xyA.25x5y2 B.25x6y2 C.5x 3y2 D.-10x6y2 4下列调查中，适宜采用全面调查（普查）方式的是（ ）A.调查一批新型节能灯泡的使用寿命 B.调查重庆全市中小学生的课外阅读时间C.调查我市初中学生的视力情况 D.调查“神州十一号”飞船零部件的安全性能5若一个多边形的每个内角都相等，且都为 160 度，则这个多边形的内角和是（ ）度A2520 B2880 C3060 D32406若 时，则代数式 的值为（ ）7yx3210xyA17 B11 C D107
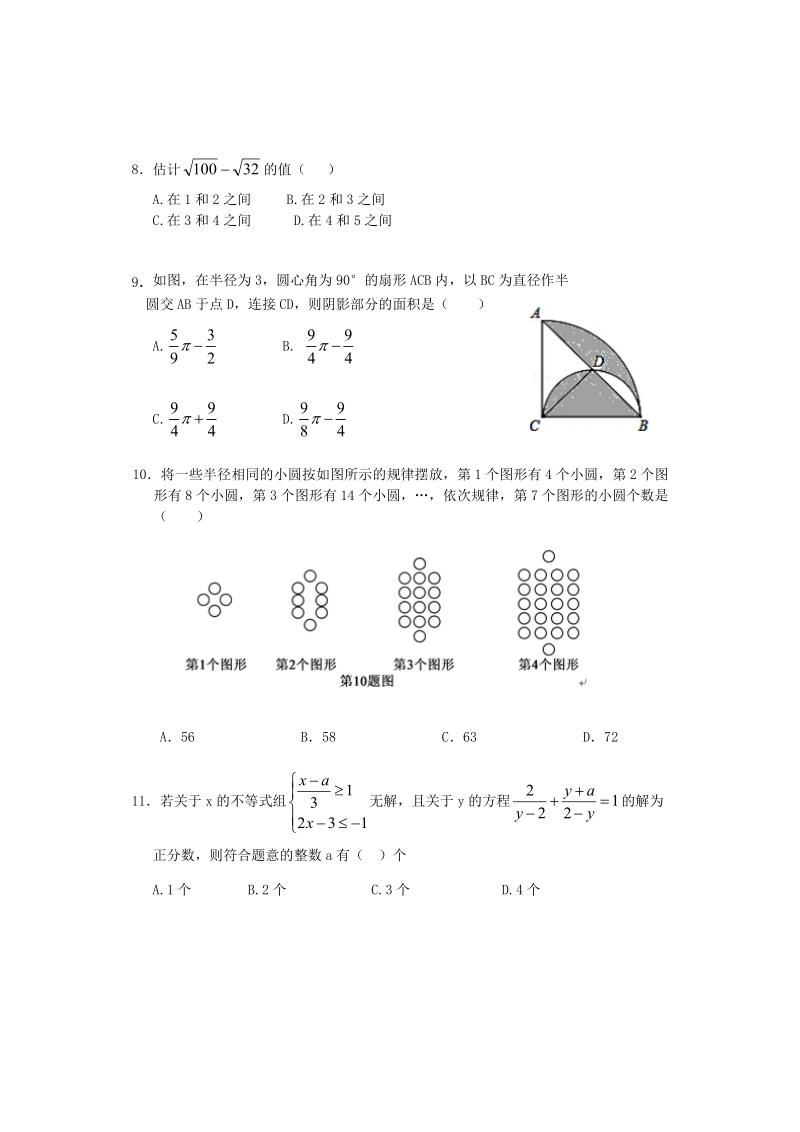
3、函数 的自变量取值范围是（ ）3xA B 03xC 且 D 且 08估计 的值（ ）3210A.在 1 和 2 之间 B.在 2 和 3 之间 C.在 3 和 4 之间 D.在 4 和 5 之间9 如图，在半径为 3，圆心角为 90的扇形 ACB 内，以 BC 为直径作半圆交 AB 于点 D，连接 CD，则阴影部分的面积是（ ）A. B. 5294C. D. 94810将一些半径相同的小圆按如图所示的规律摆放，第 1 个图形有 4 个小圆，第 2 个图形有 8 个小圆，第 3 个图形有 14 个小圆，依次规律，第 7 个图形的小圆个数是（ ）A56 B58 C63 D7211若关于 x 的不等
4、式组 无解，且关于 y 的方程 的解为132xa 12ya正分数，则符合题意的整数 a 有（ ）个A.1 个 B.2 个 C.3 个 D.4 个12如图，反比例函数 （x0）的图象经过矩形kyOABC 对角线的交点 M，分别于 AB、BC 交于点 D、E ，若四边形 ODBE 的面积为 24，则 k 的值为 （ ）A2 B4 C6 D8二、填空题：（本大题 6 个小题，每小题 4 分，共 24 分）请将每小题的答案直接填在答题卡中对应的横线上13经过多年的成长，中国城市观众到影院观影的习惯已经逐渐养成：2016 年，某影院观众人次总量才 23400，但到 2017 年已经暴涨至 1370000
5、其中 1370000 用科学记数法表示为 14计算： = 230)1(8715一个圆形人工湖如图所示，弦 AB 是湖上一座桥，已知桥 AB 长 100m ，测得圆周角ACB=45，则这个人工湖的直径 AD 为 m. x(千)y(千)O905 16.572第 15 题图 第 16 题图 第 17 题图16如图，点 是矩形 的边 上一点，把 沿 对折，使点 恰好落在EABCDADED边上的 点处。已知折痕 ，且 ，那么该矩形的周BCF10E3:4:CF长为 17甲、乙两车分别从 、 两地同时出发，相向行驶，已知甲车的速度大于乙车的速度，甲车到达 地后马上以另一速度原路返回 地(掉头的时间忽略不计)
6、，乙车到达 地以后即停在 地等待甲车如图所示为甲乙两车间的距离 (千米)与A y甲车的行驶时间 (小时)之间的函数图象，则当乙车到达 地的时候，甲车与x A地的距离为 千米第 12 题图18在一次数学探究活动课中，某同学有一块矩形纸片 ，已知 ，ABCD13， 为射线 上的一个动点，将 沿 折叠得到 ，若5ABMADMNBM是直角三角形，则所有符合条件的 点所对应的 的和为_ NC第 18 题图三、解答题：（本大题 个小题，每小题 分，共 分）解答时每小题必须给出必要2816的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上19如图，已知 EFGH，RtABC 的两个
7、顶点 A、B 分别在直线 EF、GH 上，C=90，AC 交 EF 于点 D，若 BD 平分ABC，BAH=28求BAC 的度数20为了了解重庆市的空气质量情况，我校初 2017 级“综合实践环境调查”小组从环境监测网随机抽取了若干天的空气质量作为样本进行统计，绘制了如图所示的条形统计图和扇形统计图（部分信息未给出）：（1）课题小组随机抽取的天数为 天，请将条形统计图补充完整；（2）为找出优化环境的措施，“环境治理研讨小组”的同学欲从天气质量为“中度污染”和“重度污染”的样本中随机抽取两天分析污染原因，请用列表或画树状图的方法求出所抽取的两天恰好都是“重度污染”的概率四、解答题：（本大题 5
8、个小题，每小题 10 分，共 60 分）解答时每小题必须给出必要的演算过程或推理步骤，画出必要的图形，请将解答过程书写在答题卡中对应的位置上21计算：（1） （2）2baba xyxyx1)3(422222如图，某人在山坡坡脚 C 处测得一座建筑物顶点 A 的仰角为 63.4，沿山坡向上走到 P 处再测得该建筑物顶点 A 的仰角为 53已知 BC=90 米，且 B、C、D 在同一条直线上，山坡坡度 i=5:12.（1）求此人所在位置点 P 的铅直高度 （结果精确到 0.1 米）（2）求此人从所在位置点 P 走到建筑物底部 B 点的路程（结果精确到 0.1 米）（测倾器的高度忽略不计，参考数据：
9、 345tan， 2.6tan）23每年的 3 月 15 日是 “国际消费者权益日”，许多家居商城都会利用这个契机进行打折促销活动甲卖家的某款沙发每套成本为 5000 元，在标价 8000 元的基础上打 9 折销售（1）现在甲卖家欲继续降价吸引买主，问最多降价多少元，才能使利润率不低于20%？（2）据媒体爆料，有一些卖家先提高商品价格后再降价促销，存在欺诈行为乙卖家也销售相同的沙发，其成本、标价与甲卖家一致，以前每周可售出 5 套，现乙卖家先将标价提高 ，再大幅降价 元，使得这款沙发在 3 月 15 日那一天卖出的%m40m数量就比原来一周卖出的数量增加了 ，这样一天的利润达到了 31250
10、元，求1%2.563.4 5324如图，在菱形 ABCD中， 60，点 F为边 AD上一点，连接 BF交对角线 于点 G（1）如图 1，已知 F于 ，菱形的边长为 6，求线段 G的长度；（2）如图 2，已知点 E为边 上一点，连接 CE交线段 B于点 H，且满足60H， 2H，求证： GB CA DFGHB CA DFE第 24 题图 1 第 24 题图 225已知，我们把任意形如： 的五位自然数（其中 ， ，tabccab19）称之为喜马拉雅数，例如：在自然数 中， ，所以08b 32525就是一个喜马拉雅数并规定：能被自然数 整除的最大的喜马拉雅数记为325 n，能被自然数 整除的最小的喜
11、马拉雅数记为 FnnI（1）求证：任意一个喜马拉雅数都能被 3 整除；（2）求 的值90909+21312=1122213+(8)I五、解答题：（本大题共 1 个小题，共 12 分）请把答案写在答题卡上对应的空白处，解答时每小题必须给出必要的演算过程或推理步骤26如图 1，在平面直角坐标系中，抛物线 与 x 轴交于284255yxA，C（A 在 C 的左侧），点 B 在抛物线上，其横坐标为 1，连接 BC，BO，点 F 为OB 中点.（1）求直线 BC 的函数表达式；（2）若点 D 为抛物线第四象限上的一个动点，连接 BD，CD，点 E 为 x 轴上一动点，当BCP 的面积的最大时，求点 D
12、的坐标，及 的最大值；FD（3）如图 2，若点 G 与点 B 关于抛物线对称轴对称，直线 BG 与 y 轴交于点 M，点 N 是线段 BG 上的一动点，连接 NF，MF，当 时，连接 CN，将直线 BO 绕3NOB点 O 旋转，记旋转中的直线 BO 为 BO，直线 BO 与直线 CN 交于点 Q，当OCQ为等腰三角形时，求点 Q 的坐标.第 26 题图 1 第 26 题图 2DNGM QB2018 年江北区九年级质量监测考试数学评分标准1、选择题1. D 2.C 3.A 4.D 5.B 6.A 7.B 8.D 9.B 10.B 11.C 12.D二、填空题13. 14. 15. 16. 96
13、17. 630 18. 2661037.210三、解答题19. 证明：EF/GH. 028BAH 2 分0EBA又BD 平分ABCABD=CBD=28 即ABC=2ABD=56 4 分又ABC+BAC+C=180，C=90 6 分BAC=348 分20.（1）60，图略 （2）列表，树状图略 612)(重 度 污 染P四、解答题21.（1）解：原式 分 分分523222 abba（2）原式22. 解：过 P 作 PFBD 于 F，作 PEAB 于 E斜坡的坡度 i=5:12设 PF=5x，CF=12x1 分BFPE 为矩形BF=PE PF=BE在 RTABC 中，BC=90BCAtanAB=t
14、an63.4 BC290=1802 分 22 题图AE=AB-BE=AB-PF=180-5x 3 分EP=BC+CF90+120x4 分在 RTAEP 中 3129058tanxEPA 6 分72x分 分 分524)(1231)2()(4)2(2 yxxyxxyxyxPF=5x= 7 分3.1470(2) 由（1）得 CP=13xCP=13 BC+CP=90+37.1=127.19 分1.3720答：（1）此人所在 P 的铅直高度约为 14.3 米. （2）从 P 到点 B 的路程约为 127.1 米 10 分23. 解：（1）设降价 x 元，列不等式（80000.9x）5000（1+20%）
15、2 分解得：x1800答：最多降价 1800 元，才能使得利润不低于 20%3 分（2）设 m%=a，根据题意得：8000（1+a ） 4000a50005(1+ )=312506 分a21整理得：解得： 8 分m=509 分答：m 的值为 5010 分24.（1）过 G 作 GKAD 于 K1 分在菱形 ABCD 中，ABC=60AD=AB=BC=CD=AC，FAC=60 ，AD/BCAFG CBG2 分:0328a)(12舍 去CF ADAF= AD= BC12 AFGCB 13菱形边长为 6AF=3，AG=23 分GK=AGsin60= ，AK=AGcos60=1FK=AF-AK=24
16、分在 RtFGK 中， 22FGK 5 分22(3)7（2）取 CH 的中点 M，连接 BM6 分CH=2BHCM=HM=BHHBM=HMBFHC=60， FHC=HBM+HMBHMB=30BMC=150 7 分FHC=HBC+HCB=60，ABC=HBC+ABH=60HCB=ABH8 分ABH BCM（SAS）9 分AHB=BMC=150BHE=FHC=60AHE=AHB-BHE=90AHCE 10 分25.（1）各数位数字之和 22()3()abcabcaba 是整数ab、 是整数任意一个喜马拉雅数都能被 3 整除（2） (3)90F10321269888ababab喜马拉雅数能被 8 整除 能被 8 整除32ab19,0,197ab328,64ab或可得： ()13I 890212F26.（1）直线 BC： 2 分4125yx（2） 5 分93,42D8 分max7=4FE（3）可证得 MN=MF= ，32,2N12123 4717617672, , ,4 3QQQ、 、 、分
