1、第二章 章末检测（A）(时间：120 分钟 满分：150 分)一、选择题(本大题共 12 小题，每小题 5 分，共 60 分)1在空间四边形 ABCD 的边 AB，BC，CD，DA 上分别取 E、F、G、H 四点，如果EF， GH 交于一点 P，则( )AP 一定在直线 BD 上BP 一定在直线 AC 上CP 一定在直线 AC 或 BD 上DP 既不在直线 AC 上，也不在直线 BD 上2下列推理错误的是( )AAl，A ，Bl，Bl BA，A ，B，B ABCl，AlADAl，lA 3给定下列四个命题：若一个平面内的两条直线与另一个平面都平行，那么这两个平面相互平行；若一个平面经过另一个平面
2、的垂线，那么这两个平面相互垂直；垂直于同一直线的两条直线相互平行；若两个平面垂直，那么一个平面内与它们的交线不垂直的直线与另一个平面也不垂直其中，为真命题的是( )A和 B和C和 D和4在空间中，下列说法中不正确的是( )A两组对边相等的四边形是平行四边形B两组对边平行的四边形是平行四边形C一组对边平行且相等的四边形是平行四边形D对角线互相平分的四边形是平行四边形5长方体 ABCDA 1B1C1D1 中，异面直线 AB，A 1D1 所成的角等于( )A30 B45 C60 D906正方体 ABCDA 1B1C1D1 中，二面角 C1ABC 的平面角等于( )A30 B45 C60 D907已知
3、 m，n 是不同的直线， ， 是不重合的平面，则下列命题中正确的是( )A若 m ，mn，则 n B若 m，n，则 nmC若 m，m，则 D若 ，m ，则 m8如图(1)所示，在正方形 SG1G2G3 中，E，F 分别是 G1G2 及 G2G3 的中点，D 是 EF的中点，现在沿 SE，SF 及 EF 把这个正方形折成一个四面体，使 G1，G 2，G 3 三点重合，重合后的点记为 G，如图(2) 所示，那么，在四面体 SEFG 中必有( )ASGEFG 所在平面BSDEFG 所在平面CGFSEF 所在平面DGDSEF 所在平面9如图所示，将无盖正方体纸盒展开，直线 AB、CD 在原正方体中的位
4、置关系是( )A平行B相交且垂直C异面直线D相交成 60角10矩形 ABCD 中，AB 4，BC3，沿 AC 将矩形 ABCD 折成一个直二面角BAC D，则四面体 ABCD 的外接球的体积为( )A B C D 12512 1259 1256 125311如图所示，在正方体 ABCDA1B1C1D1 中，若 E 是 A1C1 的中点，则直线 CE 垂直于( )AAC BBDCA 1D DA 1D112如图所示，将等腰直角ABC 沿斜边 BC 上的高 AD 折成一个二面角，此时B AC 60 ，那么这个二面角大小是( )A90 B60C45 D30二、填空题(本大题共 4 小题，每小题 5 分
5、，共 20 分)13设平面 平面 ，A、C，B、D ，直线 AB 与 CD 交于点 S，且点 S 位于平面 ， 之间， AS8，BS 6，CS12，则 SD_ 14如图所示，已知矩形 ABCD 中，AB3，BCa，若 PA平面 AC，在 BC 边上取点 E，使 PE DE，则满足条件的 E 点有两个时，a 的取值范围是_15如图所示，在直四棱柱 ABCDA1B1C1D1 中，当底面四边形 A1B1C1D1 满足条件_时，有 A1CB 1D1(注：填上你认为正确的一种情况即可，不必考虑所有可能的情况)16下列四个命题：若 ab，a，则 b；若 a，b ，则 ab；若a ，则 a 平行于 内所有的
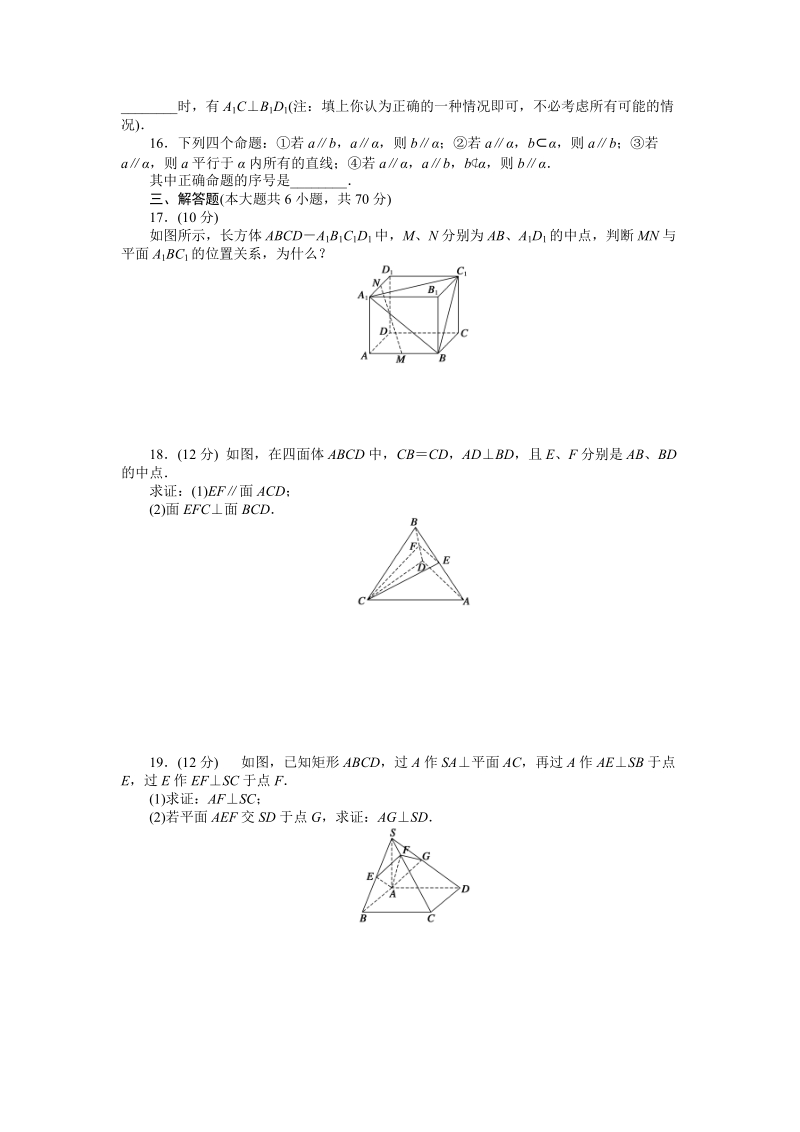
6、直线；若 a，ab，b ，则 b其中正确命题的序号是_三、解答题(本大题共 6 小题，共 70 分)17(10 分)如图所示，长方体 ABCDA 1B1C1D1 中，M、N 分别为 AB、A 1D1 的中点，判断 MN 与平面 A1BC1 的位置关系，为什么？18(12 分) 如图，在四面体 ABCD 中，CB CD，AD BD，且 E、F 分别是 AB、BD的中点求证：(1)EF面 ACD；(2)面 EFC面 BCD19(12 分) 如图，已知矩形 ABCD，过 A 作 SA平面 AC，再过 A 作 AESB 于点E，过 E 作 EFSC 于点 F(1)求证：AFSC；(2)若平面 AEF
7、交 SD 于点 G，求证：AG SD 20(12 分) 如图所示，ABCD 是正方形，O 是正方形的中心，PO底面 ABCD，底面边长为 a，E 是 PC 的中点(1)求证：PA面 BDE；平面 PAC平面 BDE；(2)若二面角 EBDC 为 30，求四棱锥 PABCD 的体积21(12 分) 如图所示，在矩形 ABCD 中，AB 3 ，BC 3，沿对角线 BD 将BCD3折起，使点 C 移到 C点，且 C点在平面 ABD 上的射影 O 恰在 AB 上(1)求证：BC平面 ACD；(2)求点 A 到平面 BCD 的距离22(12 分) 如图，在五面体 ABCDEF 中，四边形 ADEF 是正
8、方形，FA平面ABCD， BCAD，CD1，AD 2 ，BADCDA 452(1)求异面直线 CE 与 AF 所成角的余弦值；(2)证明 CD平面 ABF；(3)求二面角 BEFA 的正切值第二章 点、直线、平面之间的位置关系(A) 答案1B (如图)，PHG，HG面 ACD，P面 ACD，同理 P面 BAC，面 BAC面 ACDAC；PAC，选 B2C 若直线 lA ，显然有 l，Al，但 A3D 当两个平面相交时，一个平面内的两条直线可以平行于另一个平面，故不对；由平面与平面垂直的判定可知正确；空间中垂直于同一条直线的两条直线可以相交也可以异面，故不对；若两个平面垂直，只有在一个平面内与它
9、们的交线垂直的直线才与另一个平面垂直，故正确4A5D 由于 ADA 1D1，则BAD 是异面直线 AB，A 1D1所成的角，很明显BAD 906B7C A 中还有可能 n；B 中 nm；D 中还有可能 m 或 m 或相交不垂直；C 中，由于 m ，设过 m 的平面 与 交于 b，则 mb ，又 m，则 b，又b ，则 ，所以 C 正确8A 四边形 SG1G2G3 是正方形，SG 1G 1E，EG 1G 2F，FG 3SG 3当正方形折成四面体之后，上述三个垂直关系仍保持不变，EG，GF 成为四面体的面 EGF 的相邻两条边，因此，在四面体 SEFG 中侧棱 SGGE ，SGGF ，SG平面 E
10、FG9D 恢复成正方体(如图)，易知ABC 为等边三角形，所以ABC60选 D10C 球心 O 为 AC 中点，半径为 R AC ，12 52V R3 选 C43 125611B 证 BD面 CC1E，则 BDCE12A 连接 BC，则ABC 为等边三角形，设 ADa，则 BCAC a，BDDCa，2所以BDC90139解析 由面面平行的性质得 ACBD， ，ASBS CSSD解得 SD914a6解析 (如图)由题意知：PADE ，又 PEDE ，所以 DE面 PAE，DEAE易证ABE ECD设 BEx，则 ，即 ABCE BECD 3a x x3x 2ax90，由 0，解得 a615B 1
11、D1A 1C1(答案不唯一 )解析 由直四棱柱可知 CC1面 A1B1C1D1，所以 CC1B 1D1，要使 B1D1A 1C，只要 B1D1平面 A1CC1，所以只要 B1D1A 1C1，还可以填写四边形 A1B1C1D1 是菱形，正方形等条件16解析 中 b 可能在 内；a 与 b 可能异面；a 可能与 内的直线异面17解 直线 MN平面 A1BC1，证明如下：MD/平面 A1BC1，ND/ 平面 A1BC1MN平面 A1BC1如图，取 A1C1 的中点 O1，连接 NO1、BO 1NO 1 綊 D1C1，12MB 綊 D1C1，NO 1 綊 MB12四边形 NO1BM 为平行四边形MNB
12、O 1又BO 1平面 A1BC1，MN平面 A1BC118证明 (1)E，F 分别是 AB，BD 的中点，EF 是ABD 的中位线，EF AD ，EF面 ACD，AD 面 ACD，EF面 ACD(2)AD BD，EFAD ，EFBDCBCD，F 是 BD 的中点，CFBD 又 EFCFF，BD面 EFCBD面 BCD，面 EFC面 BCD19证明 (1)SA平面 AC，BC平面 AC，SABC，四边形 ABCD 为矩形，ABBCBC平面 SAB，BCAE又 SBAE， AE平面 SBCAESC又 EFSC ，SC 平面 AEFAFSC(2)SA 平面 AC，SADC又 ADDC，DC平面 SA
13、DDCAG又由(1)有 SC平面 AEF，AG面 AEF，SCAG，AG平面 SDC，AG SD20(1)证明 连接 OE，如图所示O、E 分别为 AC、PC 中点，OEPAOE面 BDE，PA面 BDE，PA面 BDEPO面 ABCD，PO BD在正方形 ABCD 中，BDAC，又POAC0，BD面 PAC又BD面 BDE，面 PAC面 BDE(2)解 取 OC 中点 F，连接 EFE 为 PC 中点，EF 为POC 的中位线，EFPO又PO面 ABCD，EF面 ABCDOFBD ，OE BDEOF 为二面角 EBDC 的平面角，EOF30在 Rt OEF 中，OF OC AC a，12 1
14、4 24EFOF tan 30 a，OP2EF a612 66V PABCD a2 a a313 66 61821(1)证明 点 C在平面 ABD 上的射影 O 在 AB 上，CO平面 ABD，CODA又DAAB，ABCOO ，DA平面 ABC，DA BC又BCCD，BCCD DACDD，BC 平面 ACD (2)解 如图所示，过 A 作 AECD，垂足为 E，连接 BEBC平面 ACD，BCAEAE平面 BCD故 AE 的长就是 A 点到平面 BCD 的距离ADAB，DABC，AD平面 ABC，DA AC在 Rt ACB 中，AC 3 AB2 BC 2 2在 Rt BCD 中，C DCD3
15、3在 Rt CAD 中，由面积关系，得AE AC ADC D 32333 6点 A 到平面 BCD 的距离是 622(1)解 因为四边形 ADEF 是正方形，所以 FAED所以CED 为异面直线 CE 与 AF 所成的角因为 FA平面 ABCD，所以 FACD故 EDCD在 Rt CDE 中， CD1，ED2 ，2CE 3，CD2 ED2所以 cos CED EDCE 223所以异面直线 CE 与 AF 所成角的余弦值为 223(2)证明 如图，过点 B 作 BGCD，交 AD 于点 G，则BGACDA45 由BAD45，可得 BGAB，从而 CDAB又 CDFA ，FA ABA，所以 CD平面 ABF(3)解 由(2)及已知，可得 AG ，即 G 为 AD 的中点2取 EF 的中点 N，连接 GN，则 GNEF 因为 BCAD，所以 BCEF过点 N 作 NMEF，交 BC 于点 M，则GNM 为二面角 BEF A 的平面角连接 GM，可得 AD平面 GNM，故 ADGM，从而 BCGM 由已知，可得 GM 22由 NGFA ，FA GM，得 NGGM在 Rt NGM 中，tan GNM GMNG 14所以二面角 BEF A 的正切值为 14
