 2017-2018学年广西玉林市北流市九年级(上)期中数学试卷(含答案解析)
2017-2018学年广西玉林市北流市九年级(上)期中数学试卷(含答案解析)
《2017-2018学年广西玉林市北流市九年级(上)期中数学试卷(含答案解析)》由会员分享,可在线阅读,更多相关《2017-2018学年广西玉林市北流市九年级(上)期中数学试卷(含答案解析)(16页珍藏版)》请在七七文库上搜索。
1、2017-2018 学年广西玉林市北流市九年级(上)期中数学试卷一、选择题(本大题共 12 小题,每小题 3 分,共 36 分)1 (3 分)下列方程中是关于 x 的一元二次方程的是( )Ax 2+ =0 By 23x+2=0Cx 2=5x Dx 24=(x+1) 22 (3 分)抛物线 y=(x+5) 21 的顶点坐标是( )A (5,1) B (5,1) C (5,1) D (5,1)3 (3 分)下列图形是中心对称图形的是( )A B C D4 (3 分)苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足S=gt2(g=9.8) ,则 s 与 t 的函数图象大致是( )A BC
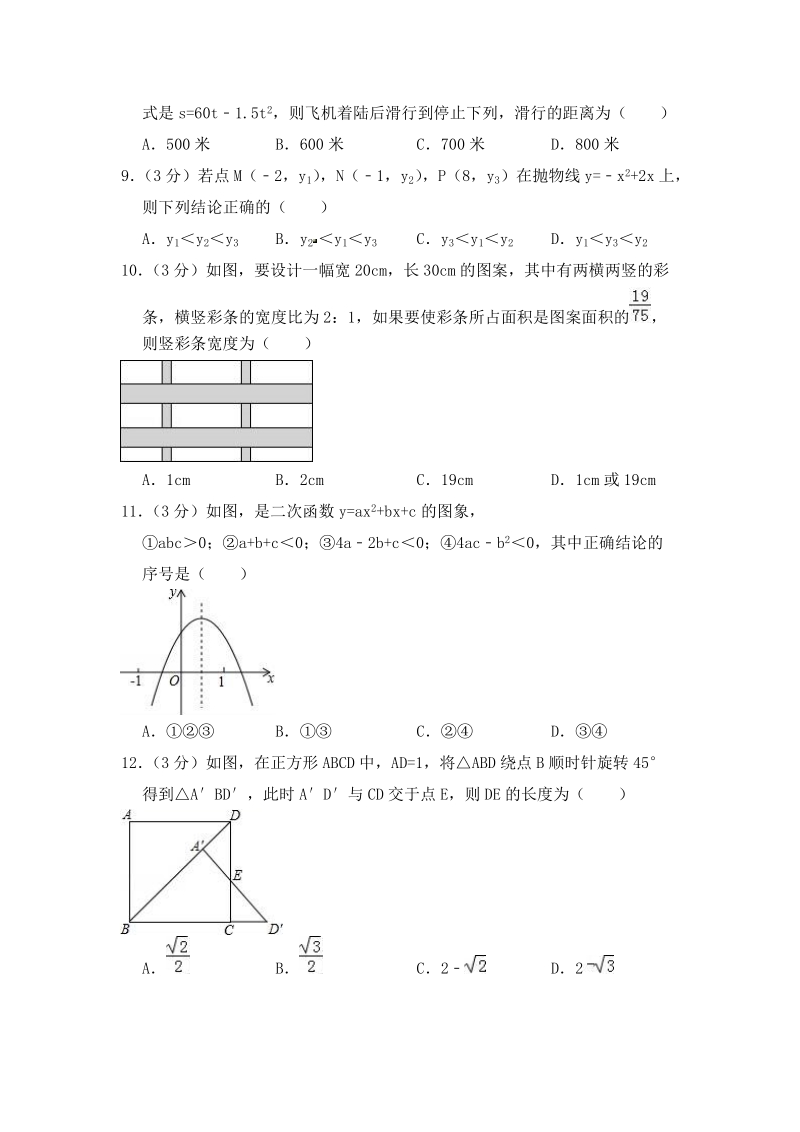
2、D5 (3 分)已知一元二次方程 x23x3=0 的两根为 与 ,则 的值为( )A1 B1 C2 D26 (3 分)在直角坐标系中,将点(2,3)关于原点的对称点向左平移 2 个单位长度得到的点的坐标是( )A (4,3) B (4,3) C (0,3) D (0,3)7 (3 分)若一元二次方程 x2+2x+a=0 的有实数解,则 a 的取值范围是( )Aa1 Ba4 Ca1 Da18 (3 分)飞机着陆后滑行的距离 s(米)关于滑行的时间 t(米)的函数解析式是 s=60t1.5t 2,则飞机着陆后滑行到停止下列,滑行的距离为( )A500 米 B600 米 C700 米 D800 米9
3、 (3 分)若点 M(2,y 1) ,N(1,y 2) ,P(8,y 3)在抛物线 y=x 2+2x 上,则下列结论正确的( )Ay 1y 2y 3 By 2 y 1y 3 Cy 3y 1y 2 Dy 1y 3y 210 (3 分)如图,要设计一幅宽 20cm,长 30cm 的图案,其中有两横两竖的彩条,横竖彩条的宽度比为 2:1,如果要使彩条所占面积是图案面积的 ,则竖彩条宽度为( )A1cm B2cm C19cm D1cm 或 19cm11 (3 分)如图,是二次函数 y=ax2+bx+c 的图象,abc0;a+b+c0;4a2b+c0;4acb 20,其中正确结论的序号是( )A B C
4、 D12 (3 分)如图,在正方形 ABCD 中,AD=1,将ABD 绕点 B 顺时针旋转 45得到ABD,此时 AD与 CD 交于点 E,则 DE 的长度为( )A B C2 D2二、填空题(本大题共 8 小题,每小题 3 分,共 24 分)13 (3 分)一元二次方程 4x2+3x1=0 的二次项系数是 14 (3 分)若 x2+6x+m2是一个完全平方式,则 m 的值是 15 (3 分)若抛物线 y=x2kx+k1 的顶点在 y 轴上,则 k= 16 (3 分)将抛物线 y=x22 向下平移 2 个单位,则得到抛物线的解析式是 17 (3 分)如图,如果把正方形 CDFE 经过旋转后能与
5、正方形 ABCD 重合,那么图形所在的平面上可作为旋转中心的点共有 个18 (3 分)为落实“两免一补”政策,某市 2011 年投入教育经费 2500 万元,预计 2013 年要投入教育经费 3600 万元已知 2011 年至 2013 年的教育经费投入以相同的百分率逐年增长,则 2012 年该市要投入的教育经费为 万元19 (3 分)已知一个二次函数,当 x0 时,函数值 y 随着 x 的增大而增大,请写出这个函数关系式 (写出一个即可)20 (3 分)RtABC 中,已知C=90,B=50,点 D 在边 BC 上,BD=2CD(如图) 把ABC 绕着点 D 逆时针旋转 m(0m180)度后
6、,如果点 B 恰好落在初始 RtABC 的边上,那么 m= 三、解答题(本大题共 8 小题,共 60 分)21 (5 分)解方程:x 28x=168x22 (5 分)解方程:(x+5) 2=6(x+5)23 (6 分)关于 x 的一元二次方程(m+1)x 2+5x+m2+3m+2=0 的常数项为 0,求m 的值24 (6 分)要组织一次篮球联赛,赛制为单循环形式(每两队之间都赛一场) ,计划安排 28 场比赛,则共有多少支球队参赛?25 (8 分)如图,四边形 ABCD 在平面直角坐标系中,(1)分别写出点 A,B,C,D 各点的坐标;(2)作出四边形 ABCD 关于原点 O 对称的四边形 A
7、BCD26 (8 分)如图,在 RtABC 中,ABC=90,AB=BC= ,将ABC 绕点 C 逆时针旋转 60得到MNC,连接 BM,交 AC 于点 O,求 BM 的长27 (10 分)某文具店购进一批纪念册,每本进价为 20 元,出于营销考虑,要求每本纪念册的售价不低于 20 元且不高于 28 元,在销售过程中发现该纪念册每周的销售量 y(本)与每本纪念册的售价 x(元)之间满足一次函数关系:当销售单价为 22 元时,销售量为 36 本;当销售单价为 24 元时,销售量为 32 本(1)请直接写出 y 与 x 的函数关系式;(2)当文具店每周销售这种纪念册获得 150 元的利润时,每本纪
8、念册的销售单价是多少元?(3)设该文具店每周销售这种纪念册所获得的利润为 w 元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?28 (12 分)如图,抛物线 y= x2+x 与 x 轴相交于 A,B 两点,顶点为 P(1)求点 A,点 B 的坐标;(2)在抛物线上是否存在点 E,使ABP 的面积等于ABE 的面积?若存在,求出符合条件的点 E 的坐标;若不存在,请说明理由参考答案与试题解析一 、选择题1 (3 分)下列方程中是关于 x 的一元二次方程的是( )Ax 2+ =0 By 23x+2=0Cx 2=5x Dx 24=(x+1) 2【解答】解:A
9、、x 2+ =0 是分式方程,故错误;B、y 23x+2=0 是二元二次方程,故错误;C、x 2=5x 是一元二次方程,故正确;D、x 24=(x+1) 2是一元一次方程,故错误,故选:C2 (3 分)抛物线 y=(x+5) 21 的顶点坐标是( )来源:学科网 ZXXKA (5,1) B (5,1) C (5,1) D (5,1)【解答】解:抛物线 y=(x+5) 21 的顶点坐标是(5,1) ,故选:D3 (3 分)下列图形是中心对称图形的是( )A B C D【解答】解:A、是中心对称图形,故本选项正确;B、不是中心对称图形,故本选项错误;C、不是中心对称图形,故本选项错误;D、不是中心
10、对称图形,故本选项错误故选:A4 (3 分)苹果熟了,从树上落下所经过的路程 s 与下落时间 t 满足S=gt2(g=9.8) ,则 s 与 t 的函数图象大致是( )A BC D【解答】解:s=gt 2是二次函数的表达式,二次函数的图象是一条抛物线又10,应该开口向上,自变量 t 为非负数,s 为非负数图象是抛物线在第一象限的部分故选:B5 (3 分)已知一元二次方程 x23x3=0 的两根为 与 ,则 的值为( )A1 B1 C2 D2【解答】解:根据题意得 +=3,=3,所以 = = =1故选:A6 (3 分)在直角坐标系中,将点(2,3)关于原点的对称点向左平移 2 个单位长度得到的点
11、的坐标是( )A (4,3) B (4,3) C (0,3) D (0,3)【解答】解:在直角坐标系中,将点(2,3)关于原点的对 称点是(2,3) ,再向左平移 2 个单位长度得到的点的坐标是(0,3) ,故选:C7 (3 分)若一元二次方程 x2+2x+a=0 的有实数解,则 a 的取值范围是( )Aa1 Ba4 Ca 1 Da1【解答】解:因为关于 x 的一元二次方程有实根,所以=b 24ac=44a0,解之得 a1故选:C8 (3 分)飞机着陆后滑行的距离 s(米)关于滑行的时间 t(米)的函数解析式是 s=60t1.5t 2,则飞机着陆后滑行到停止下列,滑行的距离为( )A500 米
12、 B600 米 C700 米 D800 米【解答】解:s=60t1.5t 2=1.5(t20) 2+600,则当 t=20 时,s 取得最大值,此时 s=600,故飞机着陆后滑行到停下来滑行的距离为:600m故选:B9 (3 分)若点 M(2,y 1) ,N(1,y 2) ,P(8,y 3)在抛物线 y=x 2+2x 上,则下列结论正确的( )Ay 1y 2y 3 By 2y 1y 3 Cy 3y 1y 2 Dy 1y 3y 2【解答】解:x=2 时,y=x 2+2x=(2) 2+2(2)=44=8,x=1 时,y=x 2+2x=(1) 2+2(1)=12=3,x=8 时,y=x 2+2x=8


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 广西 玉林市 北流市 人教版
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-28593.html