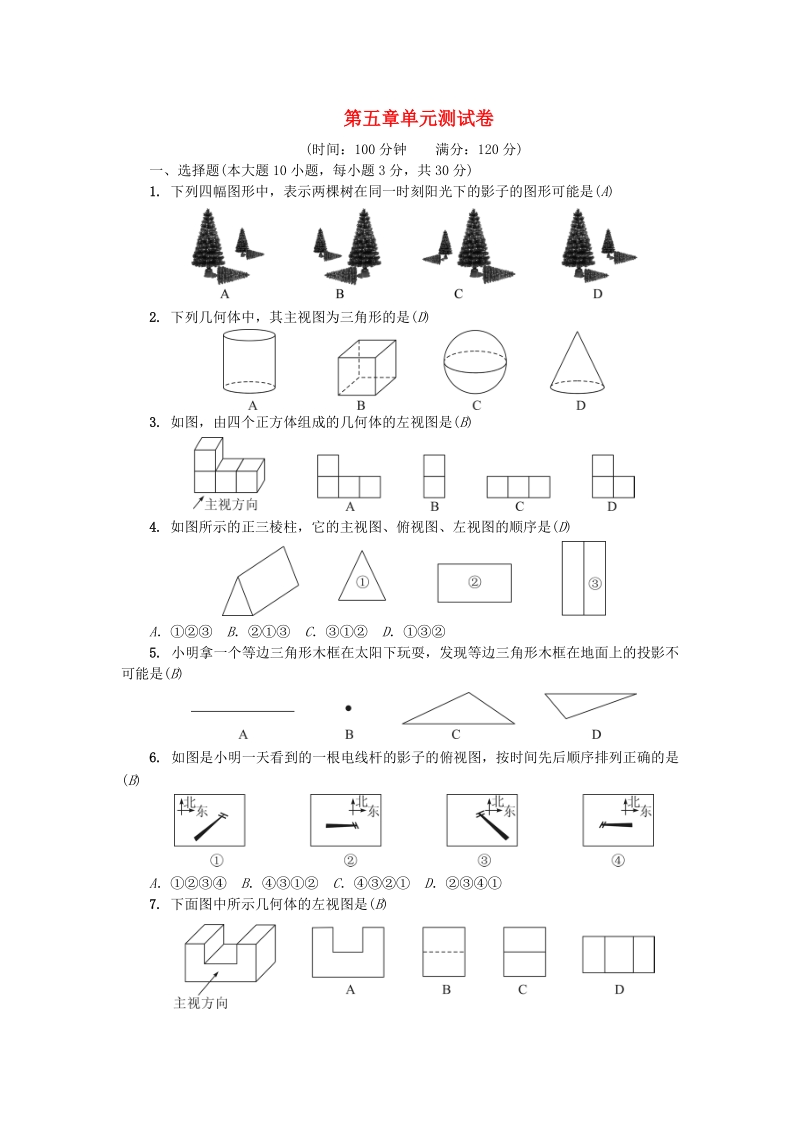
1、第五章单元测试卷(时间：100 分钟 满分：120 分)一、选择题(本大题 10小题，每小题 3分，共 30分)1. 下列四幅图形中，表示两棵树在同一时刻阳光下的影子的图形可能是( A)2. 下列几何体中，其主视图为三角形的是( D)3. 如图，由四个正方体组成的几何体的左视图是( B)4. 如图所示的正三棱柱，它的主视图、俯视图、左视图的顺序是( D)A B C D5. 小明拿一个等边三角形木框在太阳下玩耍，发现等边三角形木框在地面上的投影不可能是( B)6. 如图是小明一天看到的一根电线杆的影子的俯视图，按时间先后顺序排列正确的是(B)A B C D7. 下面图中所示几何体的左视图是( B
2、)8. 如图所示的几何体是由底面圆心在同一条直线上的三个圆柱构成的，其俯视图是( A)9. 如图是某几何题的三视图，下列判断正确的是( A)A几何体是圆柱体，高为 2 B几何体是圆锥体，高为 2C几何体是圆柱体，半径为 2 D几何体是圆锥体，半径为 2,第 9题图) ,第 10题图)10. 如图，丁轩同学在晚上由路灯 AC走向路灯 BD，当他走到点 P时，发现他身后影子的顶部刚好接触到路灯 AC的底部，当他向前再步行 20 m到达 Q点时，发现他身前影子的顶部刚好接触到路灯 BD的底部，已知丁轩同学的身高是 1.5 m，两个路灯的高度都是 9 m，则两路灯之间的距离是( D)A24 m B25
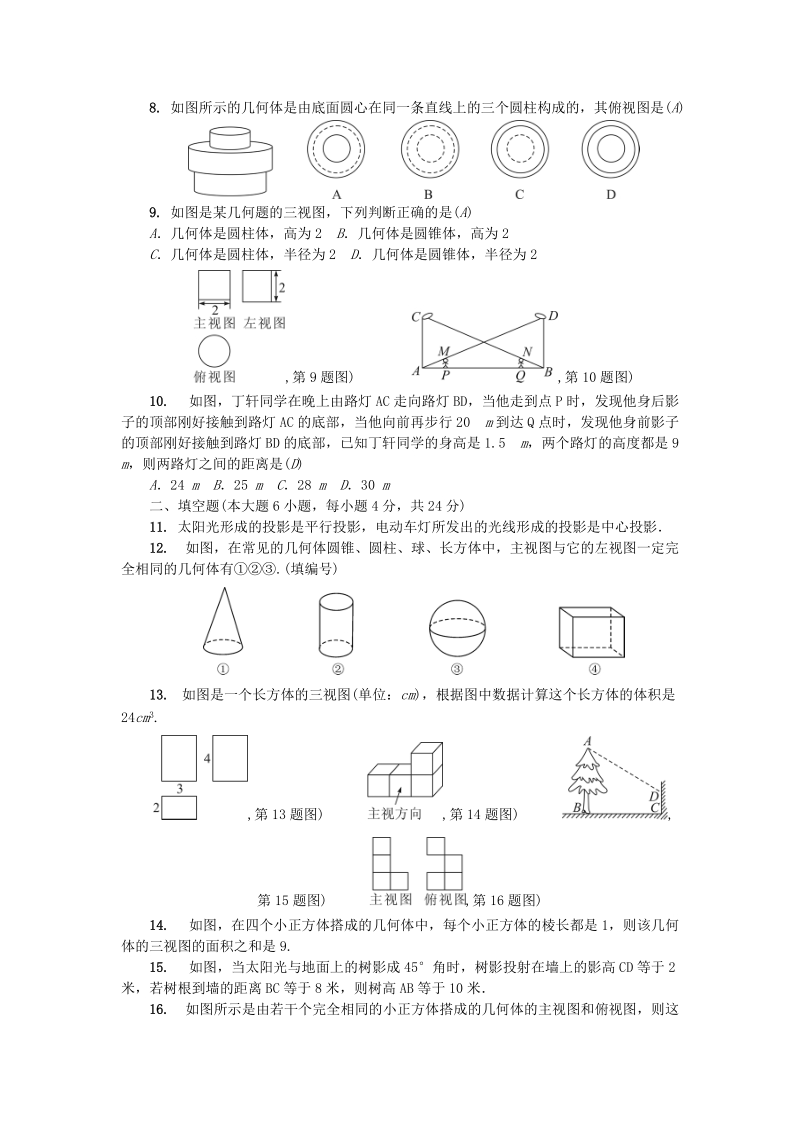
3、 m C28 m D30 m二、填空题(本大题 6小题，每小题 4分，共 24分)11. 太阳光形成的投影是平行投影，电动车灯所发出的光线形成的投影是中心投影12. 如图，在常见的几何体圆锥、圆柱、球、长方体中，主视图与它的左视图一定完全相同的几何体有.(填编号)13. 如图是一个长方体的三视图(单位： cm)，根据图中数据计算这个长方体的体积是24cm3.,第 13题图) ,第 14题图) ,第 15题图) ,第 16题图)14. 如图，在四个小正方体搭成的几何体中，每个小正方体的棱长都是 1，则该几何体的三视图的面积之和是 9.15. 如图，当太阳光与地面上的树影成 45角时，树影投射在墙
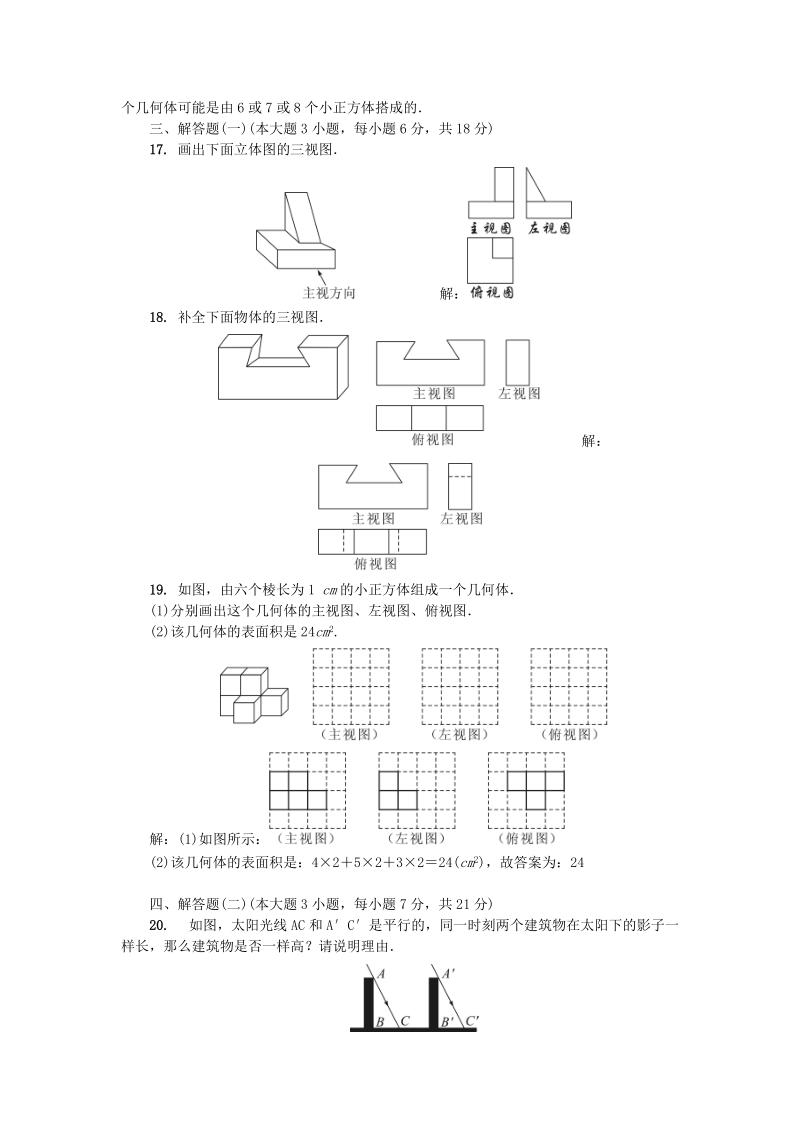
4、上的影高 CD等于 2米，若树根到墙的距离 BC等于 8米，则树高 AB等于 10米16. 如图所示是由若干个完全相同的小正方体搭成的几何体的主视图和俯视图，则这个几何体可能是由 6或 7或 8个小正方体搭成的三、解答题(一)(本大题 3小题，每小题 6分，共 18分)17. 画出下面立体图的三视图解：18. 补全下面物体的三视图解：19. 如图，由六个棱长为 1 cm的小正方体组成一个几何体(1)分别画出这个几何体的主视图、左视图、俯视图(2)该几何体的表面积是 24cm2.解：(1)如图所示：(2)该几何体的表面积是：42523224( cm2)，故答案为：24四、解答题(二)(本大题 3
5、小题，每小题 7分，共 21分)20. 如图，太阳光线 AC和 AC是平行的，同一时刻两个建筑物在太阳下的影子一样长，那么建筑物是否一样高？请说明理由解：建筑物一样高ABBC，ABBC，ABCABC90，ACAC，ACBACB，在ABC 和ABC中，ABCABC，BCBC，ACBACB，ABCABC( ASA)，ABAB.即建筑物一样高21. 在长、宽都为 4 m，高为 3 m的房间的正中央的天花板上悬挂一只白炽灯泡，为了集中光线，加上了灯罩，如图所示，已知灯罩深 8 cm，灯泡离地面 2 m，为了使光线恰好照在墙脚，问灯罩的直径应为多少？(结果精确到 0.01米)解：过点 A作 AMDE 交
6、 DE于点 M，交 BC于点 N.DEBC，ABCADE， ANAM.AN0.08，AM2，由于房间的地面为边长为 4 m的正方形，DE 为正方形的对角线，BCDE则 DE4 ，BC 0.23 m2420.08222. 在一个阳光明媚的上午，数学陈老师组织学生测量小山坡的一棵大树 CD的高度，山坡 OM与地面 ON的夹角为 30(MON30)，站立在水平地面上身高 1.7米的小明 AB在地面的影长 BP为 1.2米，此刻大树 CD在斜坡的影长 DQ为 5米，求大树的高度解：过点 Q作 QEDC 于点 E，由题意可得：ABPCEQ，则 ，故 ，ABBP ECEQ 1.71.2 ECEQ由题可得：
7、EQNO，则1230，QD5 m，DE m，EQ m，故52 532 ，解得：EC ，故 CEDE (m)，即大树的高度为1.71.2 EC532 85324 52 85324 60 85324米60 85324五、解答题(三)(本大题 3小题，每小题 9分，共 27分)23. 如图是由两个长方体组合而成的一个立体图形的三视图，根据图中所示尺寸(单位：mm)，计算出这个立体图形的表面积解：根据三视图可得：上面的长方体长 4 mm，高 4 mm，宽 2 mm，下面的长方体长 8 mm，宽 6 mm，高 2 mm，立体图形的表面积是：4424224262282268242200( mm2)24.
8、如图，某居民小区内 A，B 两楼之间的距离 MN30 m，两楼的高度都是 20 m，A楼在 B楼正南，B 楼窗户朝南B 楼内一楼住户的窗台离小区地面的距离 DN2 m，窗户高CD1.8 m当正午时刻太阳光线与地面成 30角时，A 楼的影子是否影响 B楼的一楼住户采光？若影响，挡住该住户窗户多高？若不影响，请说明理由(参考数据： 1.414，21.732， 2.236)3 5解：设光线 FE影响到 B楼的 E处，作 GEFM 于点 G，EGMN30，FEG30，FG10， MG FMGF2010 2.68.又 DN2，CD1.8， DE2.6820.681.8.A 楼3 3的影子影响到 B楼一楼采光，挡住住户窗户 0.68 m25. 用小立方体搭一个几何体，使它的主视图和俯视图如图所示，俯视图中小正方形中的字母表示在该位置小立方体的个数，请解答下列问题：(1)a3，b1，c1；(2)这个几何体最少由 9个小立方体搭成，最多由 11个小立方体搭成；(3)当 d1，e1，f2 时，画出这个几何体的左视图解：(3)左视图为
