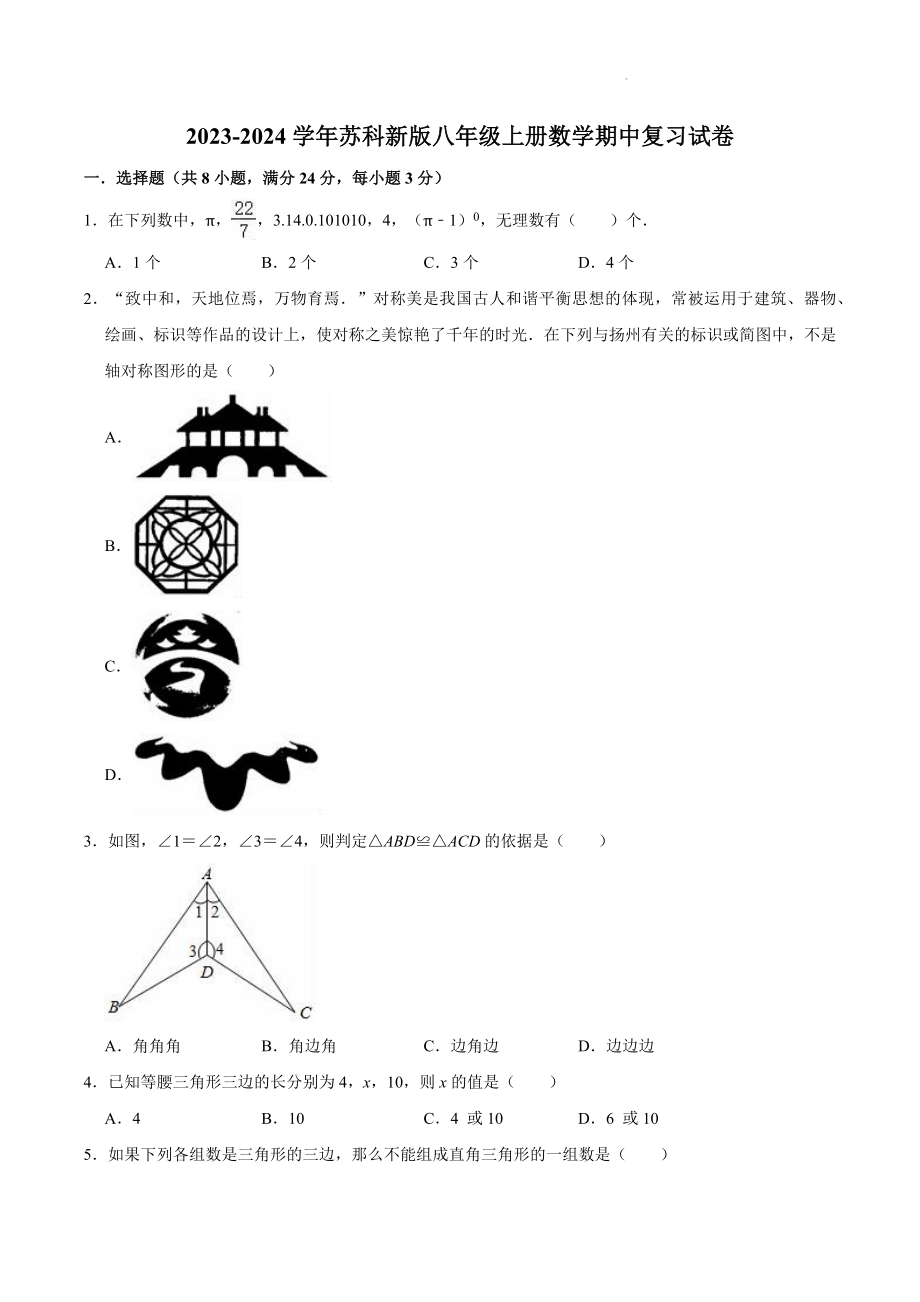
1、2023-2024学年苏科新版八年级上册数学期中复习试卷一选择题（共8小题，满分24分，每小题3分）1在下列数中，3.14.0.101010，4，（1）0，无理数有（）个A1个B2个C3个D4个2“致中和，天地位焉，万物育焉”对称美是我国古人和谐平衡思想的体现，常被运用于建筑、器物、绘画、标识等作品的设计上，使对称之美惊艳了千年的时光在下列与扬州有关的标识或简图中，不是轴对称图形的是（）ABCD3如图，12，34，则判定ABDACD的依据是（）A角角角B角边角C边角边D边边边4已知等腰三角形三边的长分别为4，x，10，则x的值是（）A4B10C4 或10D6 或105如果下列各组数是三角形的三
2、边，那么不能组成直角三角形的一组数是（）A7，24，25B5，12，13C12，16，20D4，7，86把边长为1的正方形ABCD按如图所示放置在数轴上，以原点为圆心，对角线AC为半径画弧，与数轴交于E，F两点，则点F对应的数值是（）A2BCD7如图，若ABEACF，且AB7cm，AE3cm，则EC的长为（）A3cmB4cmC5cmD7cm8如图，把直角ABC沿AD折叠后，使点B落在AC边上点E处，若AB6，AC10，则SCDE（）A15B12C9D6二填空题（共8小题，满分24分，每小题3分）9用四舍五入法将3.694精确到0.01，所得到的近似数为 10定义新运算“”：对于任意实数a，b都
3、有ababab+2（1）若3x值不大于3，则x的取值范围是 ；（2）若（2m）5的值大于3且小于9，则m的整数值是 11若+y24y+40，则x ，y 12如图，由两个直角三角形和三个正方形组成的图形其中两正方形面积分别是S122，S214，AC10，则AB 13如图，在RtABC中，ACB90，AB的垂直平分线DE交AC于E，交BC的延长线于F，垂足为D若F30，BE4，则DE的长等于 14三角形的三边长分别为cm， cm， cm，这个三角形的周长是 cm15如图，将长方形ABCD沿对角线AC折叠，点B的对应点为点E，连接CE交AD于点F，且AD2AB8，则AFC的面积为 16若三边均不相等
4、的三角形三边a、b、c满足abbc（a为最长边，c为最短边），则称它为“不均衡三角形”例如，一个三角形三边分别为7，5，4，因为7554，所以这个三角形为“不均衡三角形”（1）以下4组长度的小木棚能组成“不均衡三角形”的为 （填序号）4cm，2cm，1cm；19cm，20cm，19cm；13cm，18cm，9cm；9cm，8cm，6cm（2）已知“不均衡三角形”三边分别为2x+2，16，2x6，直接写出x的整数值为 三解答题（共11小题，满分82分）17计算：|2|+（）118计算下列各式的值（1）；（2）；（3）；19求下列各式中x的值：（1）x22；（2）（x3）3820在如图方格纸中，每
5、个小方格的边长为1请按要求解答下列问题：（1）以格点为顶点，画一个三角形ABC，使它的三边长分别为AB、BC2、CA；（2）在图中建立正确的平面直角坐标系，并写出ABC各顶点的坐标；（3）作ABC关于y轴的轴对称图形ABC（不要求写作法）；（4）直接写出ABC的面积为 21如图，已知AC，BD相交于点O，BODO，COAO，EF过点O分别交BC、AD于点E、F（1）根据所给的条件，写出图中所有的全等三角形；（2）请说明BEDF的理由22如图，河岸上A、B两点相距25km，C、D为两村庄，DAAB，CBAB，垂足分别为A、B，已知AD15km，BC10km，现要在河岸AB上建一水厂E向C，D两村
6、输送自来水，要求水厂到两村的距离相等，且DEEC，则水厂E应建在距A点多少千米处？23如图，在四边形ABCD中，ADBC，AC90，点E、F分别在AB、DC上，连接DE，BF，若AECF；求证：DEBF24如图，BD平分ABC交AC于点D，DEAB于E，DFBC于F，AB6，BC8，若SABC28，求DE的长25已知+2a，且与互为相反数，求a，b的值26如图，在RtABC中，C90，AC6cm，BC8cm点P从点A出发，沿AB以每秒4cm的速度向终点B运动当点P不与点A、B重合时，过点P作PQAB交射线BC于点Q，以PQ为一边向上作正方形PQMN，设点P的运动时间为t（秒）（1）求线段PQ的
7、长（用含t的代数式表示）（2）求点Q与点C重合时t的值（3）设正方形PQMN与ABC的重叠部分周长为1（cm），求l与t之间的函数关系式（4）作点C关于直线QM的对称点C，连接PC当PC与ABC的边垂直或重合时，直接写出t的值27已知：如图，在等腰RtABC中，ABC90，ABBC，将线段BC绕点B顺时针旋转一定角度得到线段BD连接AD交BC于点E，过点C作线段AD的垂线，垂足为点F，交BD于点G（1）如图1，若CBD45求BCG的度数；求证：CEDG；（2）如图2，若CBD60，当ACDE6时，求CE的值参考答案解析一选择题（共8小题，满分24分，每小题3分）1解：无理数有，共1个故选：A2
8、解：A、是轴对称图形，故本选项不合题意；B、是轴对称图形，故本选项不合题意；C、不是轴对称图形，故本选项符合题意；D、是轴对称图形，故本选项不合题意故选：C3解：在ADB和ADC中，ADBADC（ASA），故判定两个三角形全等最直接的依据是角边角故选：B4解：当x4时，4+410，不符合三角形三边关系，舍去；当x10时，4+1010，符合三角形三边关系故选：B5解：A、72+242252，此三角形能组成直角三角形；B、52+122132，此三角形能组成直角三角形；C、122+162202，此三角形能组成直角三角形；D、（4）2+（7）2（8）2，此三角形不能组成直角三角形故选：D6解：根据勾股
9、定理得正方形的对角线，OC，以原点为圆心，对角线AC为半径画弧，与数轴交于E，F两点，点F对应的数是故选：D7解：ABEACF，ABAC7cmECACAE734（cm）故选：B8解：在RtABC中，由勾股定理得，BC8，由翻折变换的性质可知，ABAE6，BAED90，ECACAE1064，在RtDEC中，设DEx，则BDx，DC8x，由勾股定理得，DE2+EC2CD2，x2+42（8x）2，解得x3，即DE3，SDECDEEC346，故选：D二填空题（共8小题，满分24分，每小题3分）9解：将3.694精确到0.01，所得到的近似数为3.69故答案为3.6910解：（1）3x值不大于3，3x3
10、x+23，3xx3+32，2x4，x2，即x的取值范围是x2，故答案为：x2；（2）（2m）5的值大于3且小于9，解不等式，得m，解不等式，得m，所以不等式组的解集是m，即整数m为1，故答案为：111解： +y24y+40，+（y2）20，xy0，y20，解得x2，y2，故答案为：2，212解：S122，S214，S3S1+S222+1436，BC6，AC10，AB8，故答案为：813解：C90，FDAB，而AEDCEF，AF30，DE垂直平分AB，EAEB，EBAA30，DEBE42故答案为214解：根据题意得： +4+5+5（9+5）cm；故答案为：9+515解：由折叠的性质，可知：AEA
11、B4，CECB8，EB90，ACEACBADBC，CADACB，CADACE，AFCF设AFx，则EF8x在RtAEF中，AE4，AFx，EF8x，E90，42+（8x）2x2，x5，SAFCAFAB5410故答案为：1016解：（1）1+24，4cm，2cm，1cm不能组成三角形，也就不能组成“不均衡三角形”；1919，19cm，20cm，19cm不能组成“不均衡三角形”；1813139，13cm，18cm，9cm能组成“不均衡三角形”；9886，9cm，8cm，6cm不能组成“不均衡三角形”故答案为：；（2）16（2x+2）2x+2（2x6），解得：x3，2x60，解得：x3，故不合题意，
12、舍去；2x+2162x6，解得：7x11，2x+21616（2x6），解得：x9，9x11，x为整数，x10，经检验，当x10时，22，16，14可构成三角形；2x616，解得：x11，2x+2（2x6）2x616，解得：x15，11x15，x为整数，x12或13或14，都可以构成三角形；综上所述，x的整数值为10或12或13或14，故答案为：10或12或13或14三解答题（共11小题，满分82分）17解：原式2（2）822+831018解：（1）（）2，；（2）0.330.027，0.3；（3）（1）31，119解：（1）x22，x26，；（2）（x3）38，x32，x120解：（1）如图，
13、ABC即为所求；（2）平面直角坐标系如图所示A（3，4），B（4，2），C（2，0）（答案不唯一）；（3）如图，ABC即为所求；（4）SABC241222143故答案为：321解：（1）图中所有的全等三角形：ADOCBO，AFOCEO，DFOBEO；（2）在CBO和ADO中，CBOADO（SAS），BD，在BEO和DFO中，BEODFO（ASA），BEDF22解：E站应建在离A站10km处，即AEBC10km，AB25km、AD15km，BEABAE15kmAD，CBAB、DAAB，AB90，在ADE和BEC中，ADEBEC（SAS），DECE23证明：ADBC，ADC+C180，C90，AD
14、C90，A90，ADC+A180，ABCD，四边形ABCD为平行四边形，ABCD，AECF，ABAECDCF，即BEDF，ABCD，四边形EDFB为平行四边形，DEBF24解：BD平分ABC交AC于点D，DEAB，DFBC，DEDF，AB6，BC8，SABC28，SABCSABD+SBCDABDE+BCDFDE（AB+BC）28，即DE（6+8）28，DE425解：，a21或a20或a21，a3或2或1，当a3时，b2，当a2时，当a1时，1，b，综上所述，26解：（1）在RtABC中、C90，AB10，AP4t，BP104t，PQBPtanBBP（104t）3t；（2）当点Q与点C重合时，如
15、图1所示：cosA，cosA，t（s）；（3）当0t时，如图2所示：BNABAPPN104t+3tt，tanB，NH（t），cosB，BH（t），CHBCBH8（t），tanA，PDt，cosA，ADt，CDACAD6t，lPN+NH+CH+CD+PD3t+（t）+8（t）+6t+tt+；当t时，如图3所示：同理：NH（t），BH（t），BQ（104t），HQBQBH（104t）（t），l2PQ+NH+HQ2（3t）+（t）+（104t）（t）t+；（4）当C与C重合时，PCAB，如图4所示：由（2）得：ts；当PCAC时，如图5所示：则PCBC，连接CE，点C关于直线QM的对称点C，CCMQ
16、，CECE，CCPQ，四边形CCPQ是平行四边形，CQCP，CCPQ3t，由（3）得：BQ（104t），CPCQ8（104t）+5t，PDBC，即，PDt，ADt，CDPDCPt（+5t）t，MQAB，即，CE+tCE，DEACADCE6t（+t）t，CD2+DE2CE2，即（t）2+（t）2（+t）2整理得：27t2t+0，解得：t1（s），t2（s）（不合题意舍去）；当C落在AB上时，PC与AB重合，如图6所示：点C关于直线QM的对称点C，OCOC，四边形PQMN是正方形，MQAB，ADCDAC3，DQ是CAB的中位线，CQBQBC4，由（3）得：BQ（104t），（104t）4，t（s）
17、，综上所述，当PC与ABC的边垂直或重合时，t的值为s或s或s27（1）解：BABC，ABC90，ACBCAB45，CBD45，ACBCBD，ACBD，CADD，BDBCBA，DBAD，CADBADCAB22.5，CGAD，CFD90，ACF9022.567.5，BCGACFACB22.5；证明：延长CG，AB交于T，如图：ABECBT90，ABBC，BAEBCT22.5，ABECBT（ASA），BEBT，AEBT，BAE22.5，AEB90BAE67.5T，EBGTBG45，TGB180TTBG67.5，TTGB，BTBG，BEBTBG，BCBD，BCBEBDBG，即CEDG；（2）解：连接
18、CD，过点D作DHBC于H，在DH上取一点J，使得EJDJ，设CFa，如图：CBBD，CBD60，BCD是等边三角形，ABBC，ABC90，ABD90+60150，BACACB45，BADBDA15，CAF30，CGAD，CFA90，AC2CF2a，CDB60，BDA15，FDCFCD45，FCDFa，DCBCBDa，DHBC，CHBHa，DHCHa，HDB30，JDEHDBBDA15，设EHx，JEJD，JEDJDE15，EJHJED+JDE30，EJ2EHDJ2x，HJx，DE（+）x，DHaHJ+DJ，x+2xa，x（）a，DE（3）a，ACDE6，2a（3）a6，a3（+1），CECH+EHa+（）a（）a（）3（+1）6
