 2023-2024学年广东深圳市八年级数学上册期中复习试卷(范围:1、2、3、6章)含答案
2023-2024学年广东深圳市八年级数学上册期中复习试卷(范围:1、2、3、6章)含答案
《2023-2024学年广东深圳市八年级数学上册期中复习试卷(范围:1、2、3、6章)含答案》由会员分享,可在线阅读,更多相关《2023-2024学年广东深圳市八年级数学上册期中复习试卷(范围:1、2、3、6章)含答案(18页珍藏版)》请在七七文库上搜索。
1、2023-2024学年广东深圳市八年级数学上册期中复习试卷一、选择题(本大题共10小题,每小题3分,共30分)1电影票上的“2排5号”如果用(2,5)表示,那么“5排2号”应该表示为()A(2,5)B(5,2)C(5,2)D(2,5)2下列实数中,属于无理数的是()A3.1415BCD3如图,在RtABC中,C90,AB4cm,BCcm,则AC的长为()A3cmBcmC2cmD1cm4下列计算正确的是()ABCD5(2018春宁波期末)如表为5月份宁波市某地9天的最高气温统计表:日期(号)202122232425262728温度()212119181925252120则这组数据的中位数和众数分
2、别是()A19,21B19,25C21,21D21,256下列各数中,大于3且小于4的无理数是()ABCD3.30300300037(2022厦门模拟)下列式子计算结果是负数的是()A13BC|2|D218如图,在正方形网格内,A、B、C、D四点都在小方格的格点上,则BAC+DAC()A30B45C60D909在平面直角坐标系中,点A(x2+2x,1)与点B(3,1)关于y轴对称,则x的值为()A1B3或1C3或1D3或110(2020秋罗湖区校级期末)如图,AD1,点M表示的实数是()ABC3D3二、填空题(本大题共5小题,每小题3分,共15分不需写出解答过程,请将正确答案填写在横线上)11
3、(2020福山区一模)两个最简二次根式3与是同类二次根式,则a 12(2021秋沙坪坝区校级期末)若点P(m,m+2)在x轴上,则m的值为 13(2023春武冈市期末)若y(a1)x+a21是关于x的正比例函数,则a2023的值为 14若线段ABx轴且AB3,点A的坐标为(2,1),则点B的坐标为 15(2021腾冲市模拟)如图,在矩形ABCD中,AB2,BCa,点E在边BC上,且BEa连接AE,将ABE沿AE折叠,若点B的对应点B落在矩形ABCD的边上,则a的值为 三、解答题(本大题7小题,共55分解答时应写出文字说明、证明过程或演算步骤)16(6分)(2019春仙游县期中)计算:(1)26
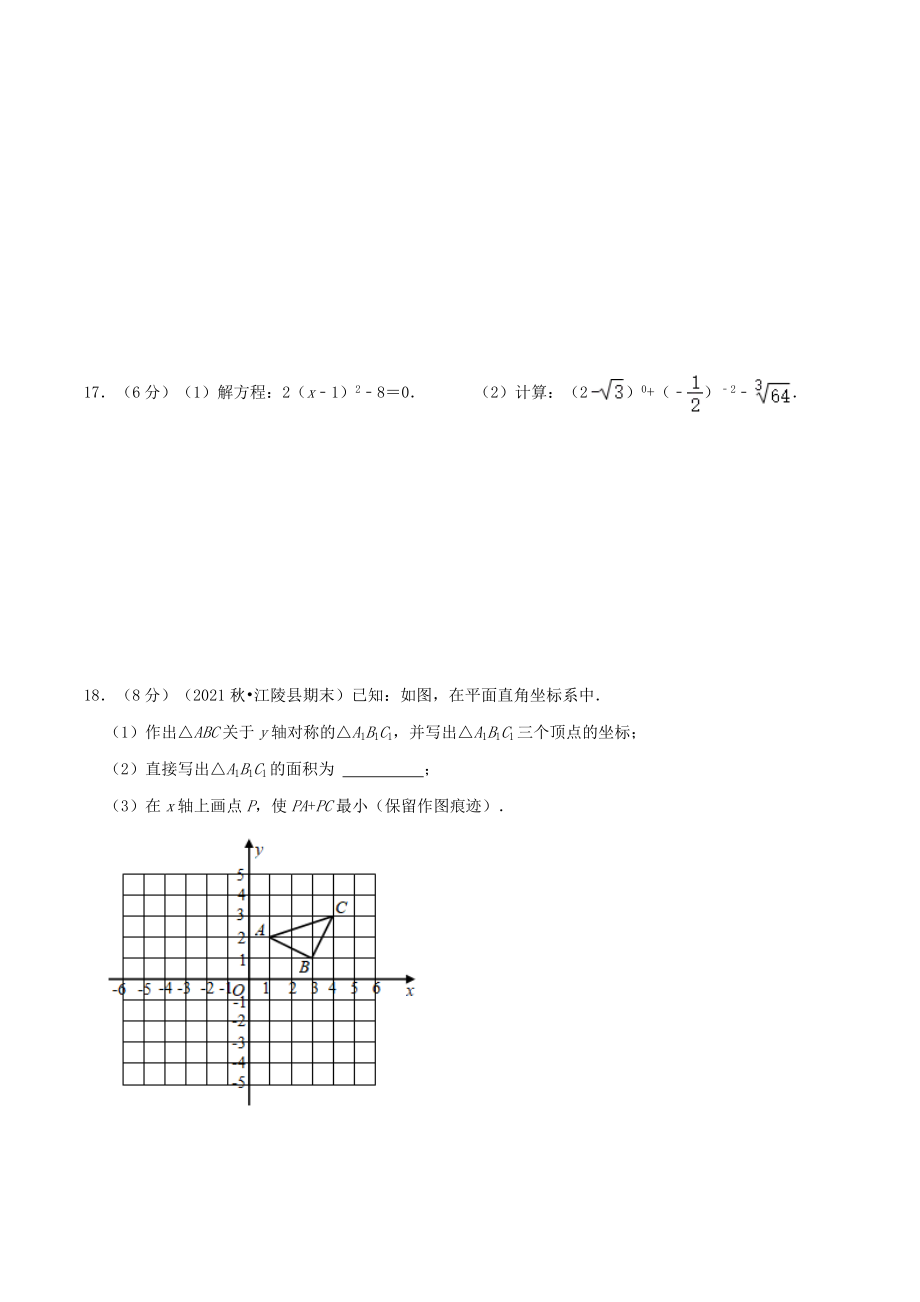
4、+3 (2)()2+2317 (6分)(1)解方程:2(x1)280 (2)计算:(2)0+()218(8分)(2021秋江陵县期末)已知:如图,在平面直角坐标系中(1)作出ABC关于y轴对称的A1B1C1,并写出A1B1C1三个顶点的坐标;(2)直接写出A1B1C1的面积为 ;(3)在x轴上画点P,使PA+PC最小(保留作图痕迹)19(8分)(2023春大安市期末)如图,小旭放风筝时,风筝线断了,风筝挂在了树上他想知道风筝距地面的高度于是他先拉住风筝线垂直到地面上,发现风筝线多出1米,然后把风筝线沿直线向后拉开5米,发现风筝线末端刚好接触地面(如图为示意图)请你帮小旭求出风筝距离地面的高度A
5、B20(7分)(2023春秦都区期中)心理学家研究发现,学生对概念的接受能力y与提出概念所用的时间x(分钟)之间有如下关系:(0x20,y的值越大,表示接受能力越强)提出概念所用的时间x(分钟)01257101213141720对概念的接受能力y4345.547.853.556.35959.859.959.858.355根据以上信息,回答下列问题:(1)在表中描述的变化过程中,自变量是什么?因变量是什么?(2)当提出概念所用的时间为10分钟时,学生的接受能力约是多少?(3)当提出概念所用的时间为多少分钟时,学生的接受能力最强?(4)在什么时间范围内,学生对概念的接受能力在逐渐增强?在什么时间范
6、围内,学生对概念的接受能力在逐渐减弱?21(10分)(2023春惠城区期中)在进行化简二次根式时,通常有如下两种方法:方法一:;方法二:;(1)请用以上两种方法化简:;(2)计算:;(3)若,求3a2+6a+5的值22(10分)(2022秋恩施市期末)通过对下面数学模型的研究学习,解决下列问题:【模型呈现】(1)如图1,BAD90,ABAD,过点B作BCAC于点C,过点D作DEAC于点E由1+22+D90,得1D又ACBAED90,可以推理得到ABCDAE进而得到AC ,BC 我们把这个数学模型称为“K字”模型或“一线三等角”模型;【模型应用】(2)如图2,BADCAE90,ABAD,ACAE
7、,连接BC,DE,且BCAF于点F,DE与直线AF交于点G求证:点G是DE的中点;如图3,在平面直角坐标系xOy中,点A的坐标为(2,4),点B为平面内任一点若AOB是以OA为斜边的等腰直角三角形,请直接写出点B的坐标2023-2024学年广东深圳市八年级数学上册期中复习试卷一、选择题(本大题共10小题,每小题3分,共30分)1电影票上的“2排5号”如果用(2,5)表示,那么“5排2号”应该表示为()A(2,5)B(5,2)C(5,2)D(2,5)解:电影票上的“2排5号”用(2,5)表示,5排2号的电影票可表示为(5,2)故选:B2下列实数中,属于无理数的是()A3.1415BCD解:A3.
8、1415是有限小数,属于有理数,故本选项不合题意;B2是整数,属于有理数,故本选项不合题意;C是无理数,故本选项符合题意;D是分数,属于有理数,故本选项不合题意;故选:C3如图,在RtABC中,C90,AB4cm,BCcm,则AC的长为()A3cmBcmC2cmD1cm解:C90,AB4cm,BCcm,AC(cm),故选:B4下列计算正确的是()ABCD解:A.+,无法合并,故此选项不合题意;B.32,故此选项符合题意;C.2,故此选项不合题意;D.2,故此选项不合题意;故选:B5(2018春宁波期末)如表为5月份宁波市某地9天的最高气温统计表:日期(号)202122232425262728温
9、度()212119181925252120则这组数据的中位数和众数分别是()A19,21B19,25C21,21D21,25解:把这些数从小到大排列为:18,19,19,20,21,21,21,25,25,最中间的数是21,则这组数据的中位数是21,21出现了3次,出现的次数最多,则这组数据的众数是21;故选:C6下列各数中,大于3且小于4的无理数是()ABCD3.3030030003解:由无限不循环小数是无理数知选项A和选项D错误,3,4,34,故选项B正确,故选:B7(2022厦门模拟)下列式子计算结果是负数的是()A13BC|2|D21解:1320,A选项符合题意;20,B选项不符合题意


- 配套讲稿:
如PPT文件的首页显示word图标,表示该PPT已包含配套word讲稿。双击word图标可打开word文档。
- 特殊限制:
部分文档作品中含有的国旗、国徽等图片,仅作为作品整体效果示例展示,禁止商用。设计者仅对作品中独创性部分享有著作权。
- 关 键 词:
- 2023 2024 学年 广东 深圳市 八年 级数 上册 期中 复习 试卷 范围 答案
 七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。
七七文库所有资源均是用户自行上传分享,仅供网友学习交流,未经上传用户书面授权,请勿作他用。



 浙公网安备33030202001339号
浙公网安备33030202001339号
链接地址:https://www.77wenku.com/p-251862.html