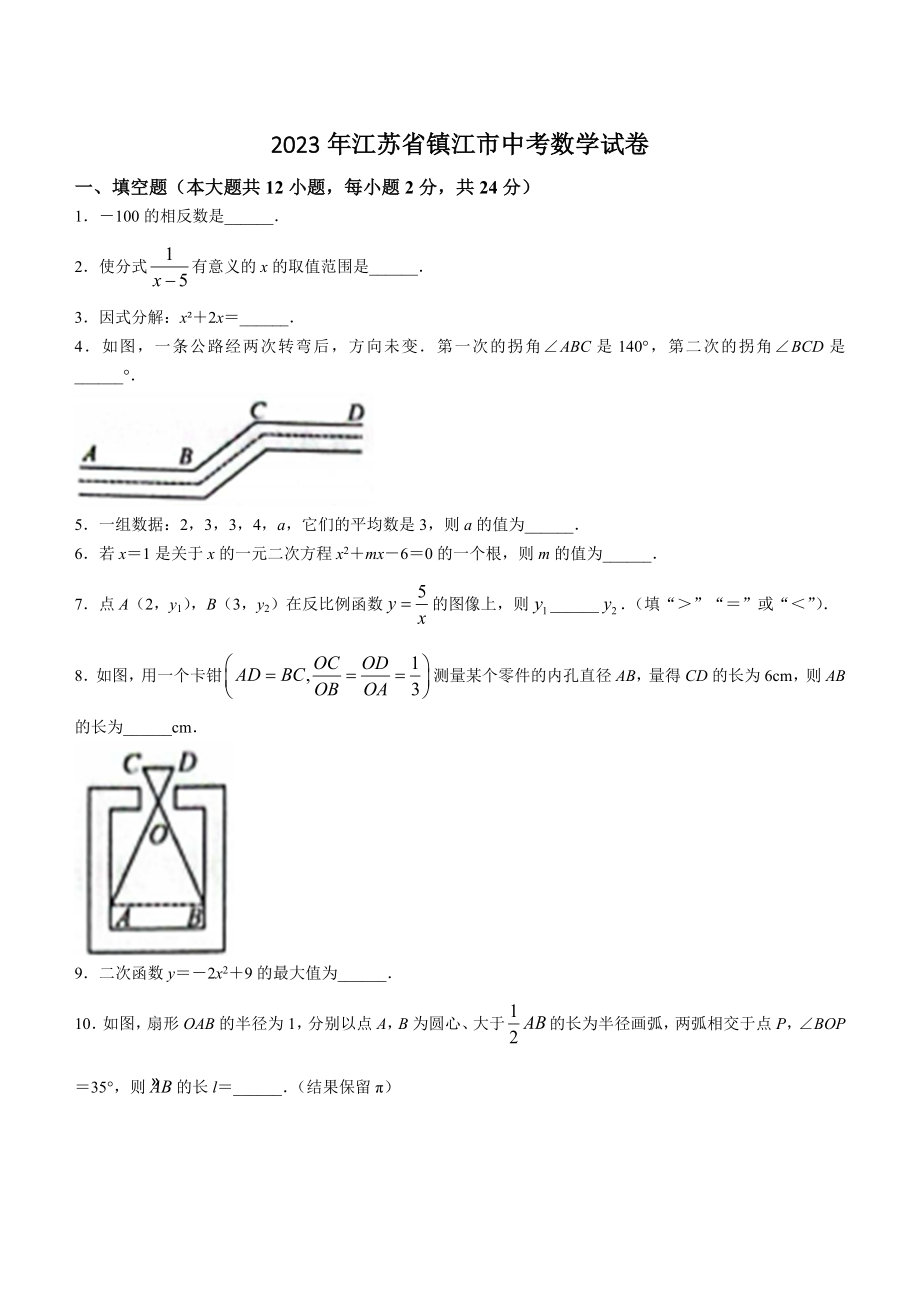
1、2023年江苏省镇江市中考数学试卷一、填空题（本大题共12小题，每小题2分，共24分）1100的相反数是_2使分式有意义的x的取值范围是_3因式分解：x2x_4如图，一条公路经两次转弯后，方向未变第一次的拐角ABC是140，第二次的拐角BCD是_5一组数据：2，3，3，4，a，它们的平均数是3，则a的值为_6若x1是关于x的一元二次方程x2mx60的一个根，则m的值为_7点A（2，y1），B（3，y2）在反比例函数的图像上，则_（填“”“”或“”）8如图，用一个卡钳测量某个零件的内孔直径AB，量得CD的长为6cm，则AB的长为_cm9二次函数y2x29的最大值为_10如图，扇形OAB的半径为1
2、，分别以点A，B为圆心、大于的长为半径画弧，两弧相交于点P，BOP35，则的长l_（结果保留）11九章算术中记载：“今有勾八步，股一十五步问勾中容圆，径几何？”译文：现在有一个直角三角形，短直角边的长为8步，长直角边的长为15步问这个直角三角形内切圆的直径是多少？书中给出的算法译文如下：如图，根据短直角边的长和长直角边的长，求得斜边的长用直角三角形三条边的长相加作为除数，用两条直角边相乘的积再乘2作为被除数，计算所得的商就是这个直角三角形内切圆的直径根据以上方法，求得该直径等于_步（注：“步”为长度单位）12已知一次函数ykx2的图像经过第一、二、四象限，以坐标原点O为圆心、r为半径作O若对于
3、符合条件的任意实数k，一次函数ykx2的图像与O总有两个公共点，则r的最小值为_二、选择题（本大题共6小题，每小题3分，共18分在每小题所给出的四个选项中，恰有一项是符合题目要求的）13圆锥的侧面展开图是（ ）A三角形B菱形C扇形D五边形14下列运算中，结果正确的是（ ）A2m2m23m4Bm2m4m3Cm4m2m2D（m2）4m615据国家统计局公布，2023年第一季度，全国居民人均可支配收入10870元数据10870用科学记数法表示为（ ）A1.087104B10.87104C10.87103D1.08710316如图，桌面上有三张卡片，一张正面朝上任意将其中一张卡片正反面对调一次，则这三
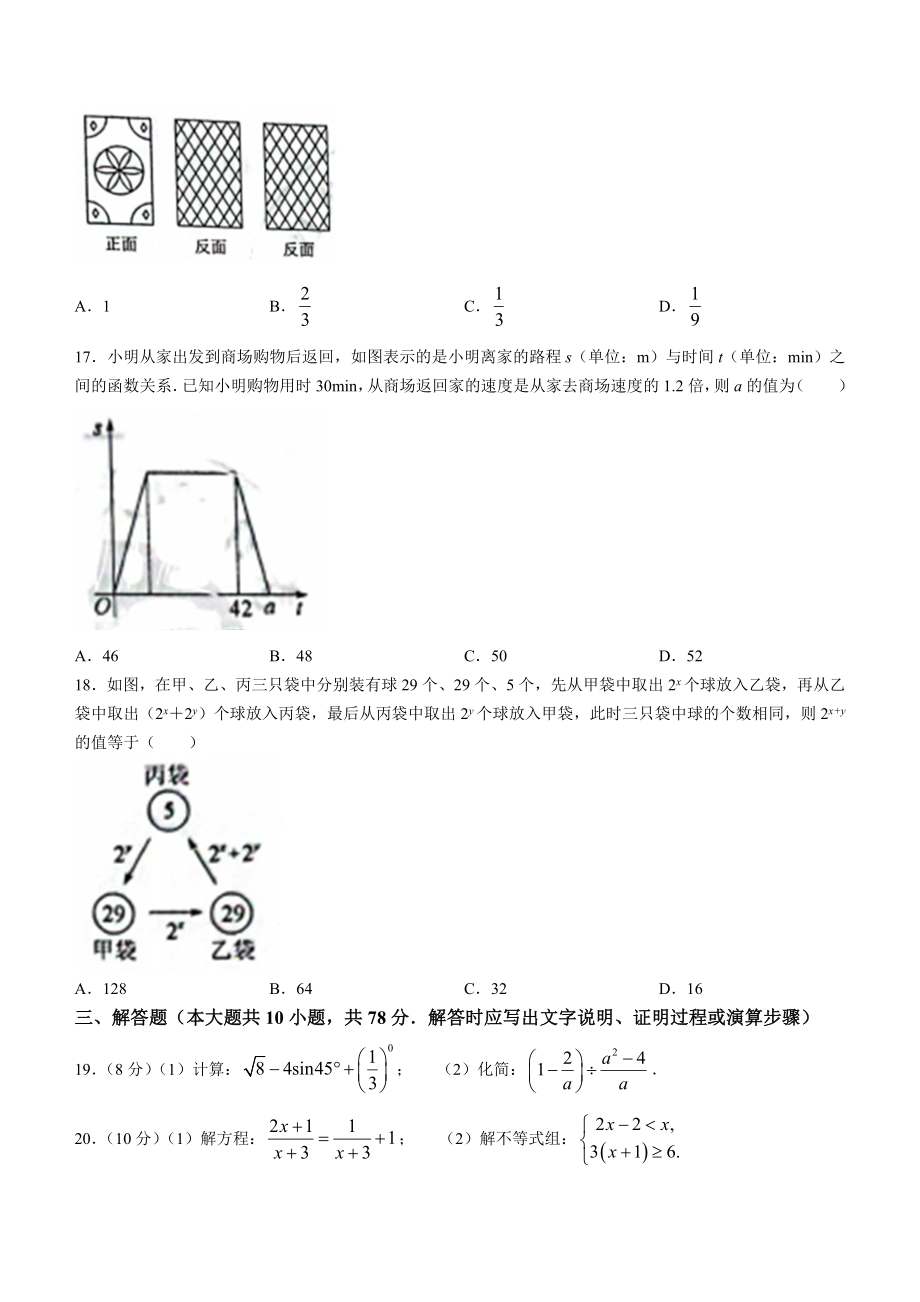
4、张卡片中出现两张正面朝上的概率是（ ）A1BCD17小明从家出发到商场购物后返回，如图表示的是小明离家的路程s（单位：m）与时间t（单位：min）之间的函数关系已知小明购物用时30min，从商场返回家的速度是从家去商场速度的1.2倍，则a的值为（ ）A46B48C50D5218如图，在甲、乙、丙三只袋中分别装有球29个、29个、5个，先从甲袋中取出2x个球放入乙袋，再从乙袋中取出（2x2y）个球放入丙袋，最后从丙袋中取出2y个球放入甲袋，此时三只袋中球的个数相同，则2x+y的值等于（ ）A128B64C32D16三、解答题（本大题共10小题，共78分解答时应写出文字说明、证明过程或演算步骤）1
5、9（8分）（1）计算：； （2）化简：20（10分）（1）解方程：； （2）解不等式组：21（6分）如图，B是AC的中点，点D，E在AC同侧，AEBD，BECD（1）求证：ABEBCD（2）连接DE，求证：四边形BCDE是平行四边形22（6分）一只不透明的袋子中装有2个红球和1个白球，这些球除颜色外都相同将球搅匀，从中任意摸出1个球后，不放回，将袋中剩余的球搅匀，再从中任意摸出1个球用列表或画树状图的方法，求两次都摸到红球的概率23（6分）香醋中有一种物质，其含量不同，风味就不同，各风味香醋中该种物质的含量如下表风味偏甜适中偏酸含量/（mg/100mL）71.289.8110.9某超市销售不同
6、包装（塑料瓶装和玻璃瓶装）的以上三种风味的香醋，小明将该超市15月份售出的香醋数量绘制成如下条形统计图已知15月份共售出150瓶香醋，其中“偏酸”的香醋占40%（1）求出a，b的值（2）售出的玻璃瓶装香醋中该种物质的含量的众数为_mg/100mL，中位数为_mg/100mL（3）根据小明绘制的条形统计图，你能获得哪些信息？（写出一条即可）24（6分）如图，正比例函数y3x与反比例函数的图像交于A，B（1，m）两点，点C在x轴负半轴上，ACO45（1）m_，k_，点C的坐标为_（2）点P在x轴上，若以B，O，P为顶点的三角形与AOC相似，求点P的坐标25（6分）如图，将矩形ABCD（ADAB）沿
7、对角线BD翻折，C的对应点为点，以矩形ABCD的顶点A为圆心、r为半径画圆，A与相切于点E，延长DA交A于点F，连接EF交AB于点G（1）求证：BEBG（2）当r1，AB2时，求BC的长26（8分）小磊安装了一个连杆装置，他将两根定长的金属杆各自的一个端点固定在一起，形成的角大小可变，将两杆各自的另一个端点分别固定在门框和门的顶部如图1是俯视图，OA，OB分别表示门框和门所在位置，M，N分别是OA，OB上的定点，OM27cm，ON36cm，MF，NF的长度固定，MFN的大小可变 图1 图2 图3（1）图2是门完全打开时的俯视图，此时，OAOB，MFN180，求MNB的度数（2）图1中的门在开合
8、过程中的某一时刻，点F的位置如图3所示，请在图3中作出此时门的位置OB（用无刻度的直尺和圆规作图，不写作法，保留作图痕迹）（3）在门开合的过程中，sinONM的最大值为_（参考数据：sin370.60，cos370.80，tan370.75）27（11分）已知，在平面直角坐标系xOy中，点A的坐标为（3，0），点B的坐标为（m，n），点C与点B关于原点对称，直线AB，AC分别与y轴交于点E，F，点F在点E的上方，EF2（1）分别求点E，F的纵坐标（用含m，n的代数式表示），并写出m的取值范围（2）求点B的横坐标m，纵坐标n之间的数量关系（用含m的代数式表示n）（3）将线段EF绕点（0，1）顺时
9、针旋转90，E，F的对应点分别是，当线段与点B所在的某个函数图像有公共点时，求m的取值范围28（11分）【发现】如图1，有一张三角形纸片ABC，小宏做如下操作： 图1 图2 图3（1）取AB，AC的中点D，E，在边BC上作MNDE；（2）连接EM，分别过点D，N作DGEM，NHEM，垂足为G，H；（3）将四边形BDGM剪下，绕点D旋转180至四边形ADPQ的位置，将四边形CEHN剪下，绕点E旋转180至四边形AEST的位置；（4）延长PQ，ST交于点F小宏发现并证明了以下几个结论是正确的：点Q，A，T在一条直线上；四边形FPGS是矩形；FQTHMN；四边形FPGS与ABC的面积相等【任务1】请
10、你对结论进行证明【任务2】如图2，在四边形ABCD中，P，Q分别是AB，CD的中点，连接PQ求证：【任务3】如图3，有一张四边形纸片ABCD，AD2，BC8，CD9，小丽分别取AB，CD的中点P，Q，在边BC上作MNPQ，连接MQ，她仿照小宏的操作，将四边形ABCD分割、拼成了矩形若她拼成的矩形恰好是正方形，求BM的长参考答案1100 解析：本题考查了相反数的概念只有符号不同的两个数互为相反数，100的相反数是1002x5 解析：本题考查了分式有意义的条件根据题意，得x50，解得x53x（x2） 解析：本题考查了用提公因式法进行因式分解x22xx（x2）4140 解析：本题考查了平行线的性质一
11、条公路经两次转弯后，方向未变，转弯前后两条道路平行，BCDABC140（两直线平行，内错角相等）53 解析：本题考查了算术平均数的计算数据2，3，3，4，a的平均数是3，解得a365 解析：本题考查了一元二次方程的解能使一元二次方程左右两边相等的未知数的值是一元二次方程的解把x1代入方程x2mx60，得1m60，解得m57 解析：本题考查了反比例函数图像上点的坐标特征、反比例函数的性质在反比例函数中，k50，该函数图像在第一、三象限，且在每一个象限内，y随x的增大而减小又023，y1y2818 解析：本题考查了对顶角的性质、相似三角形的实际应用由对顶角相等得CODAOB，又，99 解析：本题考
12、查了二次函数的最值根据二次函数的顶点式确定二次函数的最大值二次函数的表达式为y2x29，当x0时，二次函数取得最大值，为910 解析：本题考查了角平分线的作法与弧长的计算公式解答本题的关键是能根据作图痕迹正确判断出OP是角平分线，并熟记弧长计算公式由题意知，OP是AOB的平分线，AOB2BOP23570，的长116 解析：本题考查了三角形的内切圆与内切圆直径的计算公式根据勾股定理得，斜边的长为（步）由题中方法可得，该直角三角形内切圆的直径（步）122 解析：本题考查了一次函数和几何问题的综合应用ykx2的图像经过第一、二、四象限，k0由于ykx2过定点（0，2），当圆经过（0，2）时，由于直线
13、呈下降趋势，因此必然与圆有另一个交点，r的临界点是2，r的最小值是213C 解析：本题考查了圆锥的侧面展开图圆锥的侧面展开图是扇形14C 解析：本题考查了合并同类项、同底数幂的乘法运算和除法运算、幂的乘方运算2m2m23m2，故A选项错误；，故B选项错误；，故C选项正确；，故D选项错误15A 解析：本题考查了科学记数法用科学记数法表示较大的数的一般形式为a10n，其中1|a|10，n等于原数的整数位数减1，108701.08710416B 解析：本题考查了概率的计算任意将其中一张卡片正反面对调一次，共有3种情况：对调正面朝上的一张，三张正面都朝下，有1种情况；对调反面朝上的一张，有两张正面朝上
14、，有2种情况P（两张正面朝上）17D 解析：本题考查了一次函数的图像、一元一次方程的实际应用根据“从家去商场和从商场返回家路程不变”列方程求解即可设小明从家去商场的速度为xm/min，则他从商场返回家的速度为1.2xm/min根据题意，得（4230）x（a42）1.2x，解得a5218A 解析：本题考查了幂的混合运算找准数量关系，合理利用整体思想是解答本题的关键调整后，甲袋中有（292x2y）个球，乙袋中有（292y）个球，丙袋中有（52x）个球一共有2929563（个）球，且调整后三只袋中球的个数相同，调整后每只袋中有63321（个）球，52x21，292y21，19解析：本题考查了实数的混
15、合运算、分式的混合运算（1）先将算术平方根、特殊角的三角函数、零指数幂化简，然后计算可得答案；（2）先通分算出括号内的结果，再将除数中的分子进行因式分解，同时将除法运算转化为乘法运算，最后约分即可得到结果解：（1）原式（2）原式20解析：本题考查了分式方程的解法、一元一次不等式组的解法（1）先将方程两边同时乘（x3）转化为整式方程，然后再根据整式方程的解法求解，最后注意要检验；（2）先分别求出两个不等式的解集，再找出这两个解集的公共部分即可得原不等式组的解集解：（1）方程两边同时乘（x3），得2x11x3，解得x3检验：当x3时，x30，x3是原分式方程的解（2）解2x2x，得x2；解3（x1
16、）6，得x1原不等式组的解集是1x221解析：本题考查了全等三角形的判定与性质、平行四边形的判定（1）由B是AC的中点得ABBC，结合AEBD，BECD，根据全等三角形的判定定理“SSS”即可证明ABEBCD；（2）由（1）中ABEBCD得ABEBCD，进一步得，再结合BECD，根据一组对边平行且相等的四边形是平行四边形即可证明证明：（1）B是AC的中点，ABBC在ABE和BCD中，ABEBCD（SSS）（2）ABEBCD，ABEBCD，又BECD，四边形BCDE是平行四边形22解析：本题考查了用列表或画树状图的方法求概率通过画树状图列举所有等可能的结果再找出两次都摸到红球的结果，最后根据概率
17、公式求解即可解：画树状图如图所示共有6种等可能的结果，其中两次都摸到红球的结果有2种，P（两次都摸到红球）23解析：本题考查了条形统计图、中位数和众数的定义（1）由“偏酸”的香醋占总数的40%可求出两种包装“偏酸”风味香醋的总瓶数，用其减“玻璃瓶装”的瓶数即可求出a的值，用总瓶数150减条形统计图中其余所有频数即可得出b的值；（2）“玻璃瓶装”中频数最大的风味对应的浓度即为众数，把售出的三种风味对应的浓度数据由小到大排列，结合条形统计图中“玻璃瓶装”的频数求得的中间两个数据的平均数即为中位数；（3）根据题中表格和条形统计图，结合统计的意义回答即可解：（1）“偏酸”风味的瓶数为15040%60，
18、a604218，b150421838171520（2）售出的玻璃瓶装香醋中“偏甜”风味的瓶数为20，“适中”风味的瓶数为38，“偏酸”风味的瓶数为42，“偏酸”风味的香醋最多，众数为110.9mg/100mL；共有203842100（个）数据，中位数为按从小到大排列后第50个数据和第51个数据的平均数，中位数为故答案为110.9，89.8（3）答案合理即可24解析：本题考查了反比例函数与一次函数的交点问题、相似三角形的性质熟练掌握用待定系数法求函数表达式，并能利用数形结合思想和分类讨论思想分析是解答本题的关键（1）点B是两函数图像的交点，利用待定系数法求出m，k的值；根据“A，B两点关于原点对
19、称”求出点A的坐标，过点A作x轴的垂线，利用等腰直角三角形的性质，结合图形，求出点C的坐标（2）根据点P在x轴上，结合图形，排除点P在x轴负半轴上的情形，当点P在x轴正半轴上时，两个三角形中已有一对角相等，而夹角的两边的对应关系不确定，故分类讨论：AOCBOP；AOCPOB分别求出两种情况下OP的长，从而得出点P的坐标解：（1）将B（1，m）代入y3x，得m313，B（1，3）将B（1，3）代入，得，k3如图，过点A作ADx轴于点D，则ADC90点A，B关于原点O对称，A（1，3），OD1，AD3又ACO45，CDAD3，OCODCD134，C（4，0）故答案为3，3，（4，0）（2）由（1）
20、可知，B（1，3），A（1，3）当点P在x轴的负半轴上时，BOP90，BOPAOC又BOPACO，BOPCAO，BOP与AOC不可能相似当点P在x轴的正半轴上时，AOCBOP若AOCBOP，则，OAOB，OPOC4，P（4，0）；若AOCPOB，则，又，综上所述，点P的坐标为（4，0）或25解析：本题是四边形与圆的综合题，考查了矩形、圆的切线、翻折的有关性质、锐角三角函数的定义，如何作辅助线，巧用解直角三角形是解答本题的关键（1）连接AE，由切线的性质得AEB90，则AEGBEG90，由矩形的性质得BADBAF90，再由直角三角形两锐角互余得FAGF90，根据对顶角相等和同圆的半径相等得BGE
21、AGF，FAEG，然后由等角的余角相等得BGEBEG，最后由等角对等边得出结论；（2）由锐角三角函数得，得ABE30，由翻折得，由得CBD30，再由矩形对边相等得ABCD，最后在RtBCD中解直角三角形即可得出结论（1）证明：如图，连接AEA与BC相切于点E，AEB90，AEGBEG90四边形ABCD是矩形，BADBAF90，FAGF90AEAF，FAEG又BGEAGF，BGEBEG，BEBG（2）解：在RtABE中，AE1，AB2，ABE30四边形ABCD是矩形，ABC90由翻折可知，四边形ABCD是矩形，CDAB2在RtBCD中，26解析：本题考查了旋转、尺规作图、锐角三角函数的有关知识（
22、1）在RtOMN中，利用锐角三角函数求得结果；（2）以点O为圆心、ON的长为半径画弧，与以点F为圆心、FN的长为半径的弧交于点N1，N2，连接ON1，ON2，得出门OB的位置；（3）当ONM最大时，sinONM的值最大，过点O作MN的垂线段，当这条垂线段最大时，ONM最大，即当垂线段为OM即垂足为M时，ONM最大，故sinONM的最大值为解：（1）在RtOMN中，ONM37MNB18037143（2）门的位置OB如图1中OB1或OB2所示（画出其中一条即可） 图1（3）如图2，连接NM，过点O作OHNM，交NM的延长线于点H在门的开合过程中，ONM在不断变化，当ONM最大时，sinONM的值最
23、大由图2可知，当OH与OM重合时，OH取得最大值，此时ONM最大，sinONM的最大值为 图227解析：本题考查了用待定系数法求一次函数的表达式、一次函数图像上点的坐标特征、二次函数图像上点的坐标特征、旋转的性质利用数形结合思想是解答本题的关键（1）由对称的性质求出点C的坐标，设直线AB，AC的函数表达式，利用待定系数法即可求出与y轴的交点E，F的坐标；（2）点E，F都在y轴上，且点F在点E的上方，线段EF的长可用上边点的纵坐标减下边点的纵坐标表示，结合EF2化简即可得m，n之间的数量关系；（3）由旋转得，点的纵坐标为1，由点在点B所在的函数图像上，求出点的横坐标，由线段与点B所在的函数图像有
24、公共点，求出点横坐标与纵坐标的取值范围从而得出m的取值范围解：（1）由直线AB与y轴交于点E，得m3点C与点B关于原点对称，点C的坐标为（m，n）由直线AC与y轴交于点F，得m3，即m3综上所述，m3设直线AB对应的一次函数表达式为ykxb，将A（3，0），B（m，n）代入，得解得，同理可得，（2）由（1）得，又EF2，点F在点E的上方，整理得（3）n与m的关系式为，点B（m，n）在函数的图像上由旋转得，当点在点B所在的函数图像上时，解得线段与点B所在的函数图像有公共点，或由旋转得，或，或28解析：本题考查了旋转的性质、三角形的内角和定理、三点共线问题的证明、全等三角形的判定与性质、三角形的中
25、位线定理、相似三角形的判定与性质、解直角三角形、勾股定理、梯形的面积计算（1）由旋转的性质得对应角相等，即ABCQAD，ACBTAE，由三角形内角和定理得ABCBACACB180，从而得QADBACTAE180，即Q，A，T三点共线；（2）梯形中位线的证明问题常转化为三角形的中位线问题解决，连接AQ并延长，交BC的延长线于点E，证明ADQECQ，可得AQEQ，ADCE，由三角形中位线定理得；（3）过点D作DRBC于点R，由，得，从而得，由【发现】得，GE6，PE3，由【任务2】的结论得PQ5，由勾股定理得EQ4过点Q作QHBC，垂足为H由及得，从而得，证明PEQQHM，得，从而得【任务1】证法
26、1：由旋转得，QADABC，TAEACB在ABC中，ABCBACACB180，QADBACTAE180，点Q，A，T在一条直线上证法2：由旋转得，QADABC，TAEACB，点Q，A，T在一条直线上【任务2】证明：如图1，连接AQ并延长，交BC的延长线于点E，DAQEQ是CD的中点，DQCQ在ADQ和ECQ中，ADQECQ（AAS）AQEQ，ADCE又P是AB的中点，APBP，PQ是ABE的中位线， 图1【任务3】解：用【发现】的方法画出示意图如图2所示 图2由【任务2】可得，过点D作DRBC，垂足为R在RtDCR中，GE6，PE3在RtPEQ中，由勾股定理得过点Q作QHBC，垂足为HQ是CD的中点，在RtQHC中，又由勾股定理得由，得PQEQMH又PEQQHM90，PEQQHM，即，
