1、第十一章三角形一、选择题（每小题3分，共10个小题，共30分）1已知三角形的两边长分别为4cm和6cm，则这个三角形第三边的长可能是（）A1cmB8cmC11cmD12cm2ABC中，如图选项正确画出AC边上的高的图形是（）ABCD3如图，在ABC中，BD是ABC的中线，BE是ABD的中线，若AE3，则AC的长度为（）A3B6C9D124由于疫情，现在网课已经成为我们学习的一种主要方式，网课期间我们常常把手机放在一个支架上面，就可以非常方便地使用，如图，此手机能稳稳放在支架上利用的原理是（）A三角形具有稳定性B两点之间，线段最短C三角形的内角和为180D垂线段最短5（2023春达川区期中）给出
2、下列说法：从直线外一点到这条直线的垂线段叫做这个点到这条直线的距离；三角形的角平分线是射线；三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外；任何一个三角形都有三条高、三条中线、三条角平分线；三角形的三条角平分线交于一点，且这点在三角形内正确的说法有（）A1个B2个C3个D4个6（2022秋忻府区期末）如图，将ABC沿着平行于BC的直线DE折叠，点A落在点A处，若B44，则ADB的度数是（）A108B104C96D927（2022东坡区校级模拟）一个凸多边形的内角和与外角和之比为2：1，则这个多边形的边数为（）A5B6C7D88（2022秋新华区校级期末）如图，BP是ABC中ABC
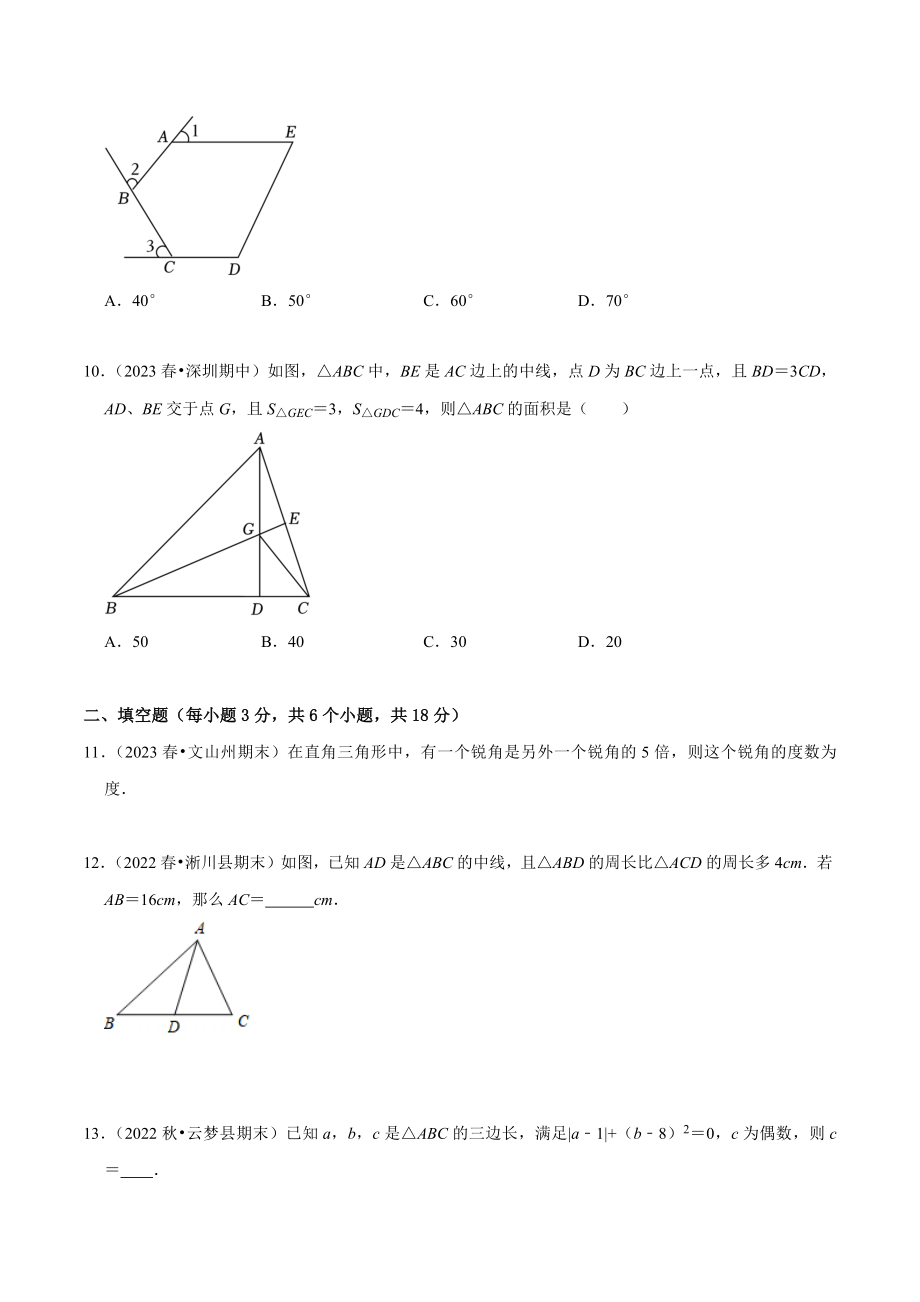
3、的平分线，CP是ACB的外角的平分线，如果ABP20，ACP50，则A+P（）A70B80C90D1009（2023肥东县模拟）如图，在五边形ABCDE中，AECD，150，270，则3的度数是（）A40B50C60D7010（2023春深圳期中）如图，ABC中，BE是AC边上的中线，点D为BC边上一点，且BD3CD，AD、BE交于点G，且SGEC3，SGDC4，则ABC的面积是（）A50B40C30D20二、填空题（每小题3分，共6个小题，共18分）11（2023春文山州期末）在直角三角形中，有一个锐角是另外一个锐角的5倍，则这个锐角的度数为 度12（2022春淅川县期末）如图，已知AD是A
4、BC的中线，且ABD的周长比ACD的周长多4cm若AB16cm，那么AC cm13（2022秋云梦县期末）已知a，b，c是ABC的三边长，满足|a1|+（b8）20，c为偶数，则c14（2023春乳山市期末）如图，若E50，则A+B+C+D 15（2022秋湟中区校级月考）一个四边形截去一个角后，所形成的一个新多边形的边数是 16（2023春济南期中）如图，D、E分别是ABC边AB、BC上的点，AD3BD，BECE，设ADF的面积为S1，CEF的面积为S2，若SABC8，则S1S2的值为 三、解答题（共9个小题，共72分）17（6分）（2022秋咸阳校级期末）如图，在ABC中，AD是ABC的角
5、平分线，DEAC于点E，若B42，C58求ADC及ADE的度数18（6分）（2023春贵州期末）已知一个多边形的边数为a（1）若该多边形的内角和的14比外角和多90，求a的值；（2）若该多边形是正多边形，且其中一个内角为108，求a的值19（7分）（2022秋乌鲁木齐县月考）已知a，b，c是ABC的三边长，a4，b6，设ABC的周长是x（1）求c与x的取值范围；（2）若x是小于18的偶数，试判断ABC的形状20（7分）（2022春石狮市校级期中）如图，CE是ABC的外角ACD的平分线，且CE交BA的延长线于点E（1）若B30，BAC130，求E的度数；（2）求证：BACB+2E21（8分）如图
6、，在ABC中，ABAC，腰AC上的中线BD把ABC的周长分成15和21两部分，求ABC各边的长22（8分）（2022秋淮南期末）（1）如图1，有一块直角三角板XYZ放置在ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、CABC中，A30，则ABC+ACB ，XBC+XCB （2）如图2，ABC的位置不变，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C，那么ABX+ACX的大小是否变化？若变化，请举例说明；若不变化，请求出ABX+ACX的大小23（9分）（2023春高新区期中）如图，在ABC中，ADBC于D，AE平分BAC（1）若C70，B40，
7、求DAE的度数（2）若CB30，则DAE （3）若CB（CB），求DAE的度数（用含的代数式表示）24（9分）（2022秋城关区校级期末）如图1，一张三角形ABC纸片，点D，E分别是ABC边上两点研究（1）：如果沿直线DE折叠，使点A落在CE上的点A处，则BDA与A的数量关系是 ；研究（1）：如果折成图2的形状，猜想BDA，CEA和A的数量关系是 ；研究（3）：如果折成图3的形状，猜想BDA，CEA和A的数量关系是什么，并说明理由25（12分）（2023春天宁区校级期中）在ABC中，BD平分ABC交AC于点D，点E是线段AC上的动点（不与点D重合），过点E作EFBC交射线BD于点F，CEF的角
8、平分线所在直线与射线BD交于点G（1）如图，点E在线段AD上运动若ABC40，C60，则BGE的度数是 ；若A70，则BGE ；探究BGE与A之间的数量关系，并说明理由；（2）若点E在线段DC上运动时，BGE与A之间的数量关系与（1）中的数量关系是否相同？若不同，请直接写出BGE与A之间的数量关系，不需说理第十一章三角形一、选择题（每小题3分，共10个小题，共30分）1已知三角形的两边长分别为4cm和6cm，则这个三角形第三边的长可能是（）A1cmB8cmC11cmD12cm【分析】已知三角形的两边长分别为4cm和6cm，根据在三角形中任意两边之和第三边，任意两边之差第三边；即可求第三边长的范
9、围【解答】解：设第三边长为xcm，则由三角形三边关系定理得64x4+6，即2x10因此，本题的第三边应满足2x10，把各项代入不等式符合的即为答案1，11，12都不符合不等式2x10，只有8符合不等式，故答案为8cm故选：B【点评】本题考查了三角形三边关系，此类求三角形第三边的范围的题，实际上就是根据三角形三边关系定理列出不等式，然后解不等式即可2ABC中，如图选项正确画出AC边上的高的图形是（）ABCD【分析】根据高线的定义进行作答即可【解答】解：AC边上的高就是过B作垂线垂直AC交CA的延长线于D点，因此只有选项B符合条件，故选：B【点评】本题考查画高线熟练掌握高线是从三角形的一个顶点出发
10、，到对边的垂线段，是解题的关键3如图，在ABC中，BD是ABC的中线，BE是ABD的中线，若AE3，则AC的长度为（）A3B6C9D12【分析】根据中线的性质即可求解【解答】解：BE是ABD的中线，AD2AE6，BD是ABC的中线，AC2AD12，故选：D【点评】本题考查中线的性质，熟记知识点是关键4由于疫情，现在网课已经成为我们学习的一种主要方式，网课期间我们常常把手机放在一个支架上面，就可以非常方便地使用，如图，此手机能稳稳放在支架上利用的原理是（）A三角形具有稳定性B两点之间，线段最短C三角形的内角和为180D垂线段最短【分析】根据三角形具有稳定性进行求解即可【解答】解：由图可知，手机和
11、支架组成了一个三角形，而三角形具有稳定性，所以手机能稳稳放在支架上故选：A【点评】本题主要考查了三角形的稳定性，熟知三角形具有稳定性是解题的关键5（2023春达川区期中）给出下列说法：从直线外一点到这条直线的垂线段叫做这个点到这条直线的距离；三角形的角平分线是射线；三角形的高所在的直线交于一点，这一点不在三角形内就在三角形外；任何一个三角形都有三条高、三条中线、三条角平分线；三角形的三条角平分线交于一点，且这点在三角形内正确的说法有（）A1个B2个C3个D4个【分析】根据三角形的高、角平分线的概念、点到这条直线的距离的概念判断即可【解答】解：从直线外一点到这条直线的垂线段的长度叫做这个点到这条
12、直线的距离，故本小题说法错误；三角形的角平分线是线段，故本小题说法错误；三角形的高所在的直线交于一点，这一点在三角形内或在三角形外或在三角形的一边上，故本小题说法错误；任何一个三角形都有三条高、三条中线、三条角平分线，说法正确；三角形的三条角平分线交于一点，且这点在三角形内，说法正确；故选：B【点评】本题考查的是三角形的高、角平分线的概念、点到这条直线的距离，掌握它们的概念是解题的关键6（2022秋忻府区期末）如图，将ABC沿着平行于BC的直线DE折叠，点A落在点A处，若B44，则ADB的度数是（）A108B104C96D92【分析】根据两直线平行，同位角相等可得ADEB，再根据翻折变换的性质
13、可得ADEADE，然后根据平角等于180列式计算即可得解【解答】解：ABC沿着平行于BC的直线折叠，点A落到点A，ADEB44，ADEADE44，ADB180444492，故选：D【点评】本题考查了平行线的性质，翻折变换的性质，三角形的内角和定理，熟记性质并准确识图理清图中各角度之间的关系是解题的关键7（2022东坡区校级模拟）一个凸多边形的内角和与外角和之比为2：1，则这个多边形的边数为（）A5B6C7D8【分析】设多边形有n条边，则内角和为180（n2），再根据内角和等于外角和2倍可得方程180（n2）3602，再解方程即可【解答】解：设多边形有n条边，由题意得：180（n2）3602，解
14、得：n6，故选：B【点评】此题主要考查了多边形的内角和和外角和，关键是掌握内角和为180（n2）8（2022秋新华区校级期末）如图，BP是ABC中ABC的平分线，CP是ACB的外角的平分线，如果ABP20，ACP50，则A+P（）A70B80C90D100【分析】根据角平分线的定义以及一个三角形的外角等于与它不相邻的两个内角和，可求出A的度数，根据补角的定义求出ACB的度数，根据三角形的内角和即可求出P的度数，即可求出结果【解答】解：BP是ABC中ABC的平分线，CP是ACB的外角的平分线，又ABP20，ACP50，ABC2ABP40，ACM2ACP100，AACMABC60，ACB180AC
15、M80，BCPACB+ACP130，PBC20，P180PBCBCP30，A+P90，故选：C【点评】本题考查了三角形的外角性质，三角形的内角和定理，解答的关键是明确：一个三角形的外角等于与它不相邻的两个内角和以及补角的定义以及三角形的内角和为1809（2023肥东县模拟）如图，在五边形ABCDE中，AECD，150，270，则3的度数是（）A40B50C60D70【分析】利用多边形的内角和公式求得五边形的内角和，再由平行线性质求得D+E的和，继而求得BAE+ABC+BCD的和，最后利用角的和差即可求得答案【解答】解：四边形ABCDE为五边形，其内角和为（52）180540，AECD，D+E1
16、80，BAE+ABC+BCD540180360，1+2+31803360180，150，270，3180507060，故选：C【点评】本题主要考查多边形的内角和及平行线的性质，结合已知条件求得BAE+ABC+BCD的和是解题的关键10（2023春深圳期中）如图，ABC中，BE是AC边上的中线，点D为BC边上一点，且BD3CD，AD、BE交于点G，且SGEC3，SGDC4，则ABC的面积是（）A50B40C30D20【分析】首先根据三角形的中位线把三角形分成面积相同的两部分，可得SAGESGEC3，进而求出SACD；然后根据BD3CD，可得SABD3SADC，据此求出SABD；最后把ABD和AC
17、D的面积求和，求出ABC的面积是多少即可【解答】解：BE为ABC的中线，SAGESGEC3，SACDSAGE+SGEC+SGDC3+3+410，BD3DC，SABD3SADC31030，SABCSABD+SACD30+1040，即ABC的面积是40方法二：BD3CD，SGDC4，SBDG3SGDC12，SBCGSGDC+SBDG16，SGEC3，SBCESBCG+SGEC19，BE是AC边上的中线，SABC2SBCE38故SABC面积为：40或38（试题不严谨，两个答案都正确）故选：B【点评】此题主要考查了三角形的面积的求法，要熟练掌握，解答此题的关键是要明确：（1）三角形的中位线把三角形分成
18、面积相同的两部分（2）三角形的高一定时，面积和底成正比二、填空题（每小题3分，共6个小题，共18分）11（2023春文山州期末）在直角三角形中，有一个锐角是另外一个锐角的5倍，则这个锐角的度数为 度【分析】设较小的锐角是x度，则另一角是5x度再根据直角三角形的两个角互余列方程求解即可【解答】解：设较小的锐角是x度，则另一角是5x度则x+5x90，解得：x15故答案为：15【点评】本题主要考查了直角三角形的性质、一元一次方程的应用等知识点，掌握直角三角形的两锐角互余是解答本题的关键12（2022春淅川县期末）如图，已知AD是ABC的中线，且ABD的周长比ACD的周长多4cm若AB16cm，那么A
19、C cm【分析】利用三角形中线的性质解决问题即可【解答】解：AD是ABC的中线，又ABD的周长比ACD的周长多4cmABAC4cm，AB16cm，AC12cm故答案为12【点评】本题考查三角形的角平分线，中线，高等知识，解题的关键是熟练掌握基本知识，属于中考常考题型13（2022秋云梦县期末）已知a，b，c是ABC的三边长，满足|a1|+（b8）20，c为偶数，则c【分析】根据非负数的性质列式求出a、b的值，再根据三角形的任意两边之和大于第三边，两边之差小于第三边求出c的取值范围，再根据c为偶数求出c的值【解答】解：|a1|+（b8）20，a10，b80，解得a1，b8，根据三角形的三边关系，
20、得81c8+1，即：7c9，又c为偶数，c8故答案为：8【点评】本题考查了三角形三边关系定理：三角形两边之和大于第三边在运用三角形三边关系判定三条线段能否构成三角形时并不一定要列出三个不等式，只要两条较短的线段长度之和大于第三条线段的长度即可判定这三条线段能构成一个三角形14（2023春乳山市期末）如图，若E50，则A+B+C+D 【分析】有多种思路和解法可以将多个角的和集中在一个三角形内，例如延长CE、DE交AB于点M、N，利用外角定理就可将A+C+B+D集中在EMN中，再利用对顶角相等将E也转化到EMN中，从而使问题得解【解答】解：分别延长CE、DE与AB交于点M、N由已知E50，即CED
21、50则MENCED50（对顶角相等）EMNA+C，ENMB+D，EMN+ENMA+C+B+D，EMN+ENM180MEN18050130，A+C+B+D130故答案为：130【点评】此题考查三角形内角和定理，解题关键在于求得EMN+ENMA+C+B+D15（2022秋湟中区校级月考）一个四边形截去一个角后，所形成的一个新多边形的边数是 【分析】根据一个四边形截去一个角后得到的多边形的特点解答即可【解答】解：一个四边形截去一个角后得到的多边形可能是三角形，可能是四边形，也可能是五边形故答案为：3或4或5【点评】本题考查了多边形，能够得出一个四边形截去一个角后得到的图形有三种情形是解题的关键16（
22、2023春济南期中）如图，D、E分别是ABC边AB、BC上的点，AD3BD，BECE，设ADF的面积为S1，CEF的面积为S2，若SABC8，则S1S2的值为 【分析】根据SABC8，AD3BD，BECE，可推出SABE=12SABC，SCBD=14SABC，最后根据S1S2SABESCBD计算即可【解答】解：SABC8，AD3BD，BECE，SABE=12SABC=128=4，SCBD=14SABC=148=2，S1S2SABESCBD422，故答案为：2【点评】本题考查了三角形的面积计算，熟知等高不同底的三角形面积比为底之比是解题关键三、 解答题（共9个小题，共72分）17（6分）（202
23、2秋咸阳校级期末）如图，在ABC中，AD是ABC的角平分线，DEAC于点E，若B42，C58求ADC及ADE的度数【分析】根据三角形内角和定理求出BAC，根据角平分线的定义和已知得到BADDAC，进而根据直角三角形的锐角互余求出ADE即可【解答】解：B42，C58，BAC180425880，AD平分BAC，BADDAC40，ADC180DACC180405882，DEAC，AED90，ADE90DAC50【点评】本题考查的是角平分线的定义、三角形内角和定理的应用，掌握三角形内角和等于180、角平分线的定义是解题的关键18（6分）（2023春贵州期末）已知一个多边形的边数为a（1）若该多边形的内
24、角和的14比外角和多90，求a的值；（2）若该多边形是正多边形，且其中一个内角为108，求a的值【分析】（1）根据多边形的内角和与外角和列方程求得a的值即可；（2）根据正多边形的性质及多边形的内角和列得方程解得a的值即可【解答】解：（1）由题意可得14（a2）18036090，解得：a12；（2）由题意可得108a（a2）180，解得：a5【点评】本题考查多边形的内角与外角及正多边形的性质，它们均为基础且重要知识点，必须熟练掌握19（7分）（2022秋乌鲁木齐县月考）已知a，b，c是ABC的三边长，a4，b6，设ABC的周长是x（1）求c与x的取值范围；（2）若x是小于18的偶数，试判断ABC
25、的形状【分析】（1）利用三角形三边关系进而得出c的取值范围，进而得出答案；（2）利用等腰三角形的判定方法得出即可【解答】解：（1）因为a4，b6，所以2c10故周长x的范围为12x20（2）因为周长为小于18的偶数，所以x16或x14当x为16时，c6；当x为14时，c4当c6时，bc，ABC为等腰三角形；当c4时，ac，ABC为等腰三角形综上，ABC是等腰三角形【点评】此题主要考查了等腰三角形的判定和三角形三边关系，得出c的取值范围是解题关键20（7分）（2022春石狮市校级期中）如图，CE是ABC的外角ACD的平分线，且CE交BA的延长线于点E（1）若B30，BAC130，求E的度数；（2
26、）求证：BACB+2E【分析】（1）由三角形的外角性质可求得ACD160，再由角平分线的定义可得ECD80，即可求得E的度数；（2）由角平分线的定义可得ECDECA，再由三角形的外角性质可得ECDB+E，BACECA+E，即可求解【解答】（1）解：B30，BAC130，ACDB+BAC160，CE平分ACD，ECD=12ACD80，EECDB50；（2）证明CE平分ACD，ECDECA，ECDB+E，BACECA+E，BACB+E+EB+2E【点评】本题主要考查三角形的外角性质，角平分线的定义，解答的关键是结合图形分析清楚各角之间的关系21（8分）如图，在ABC中，ABAC，腰AC上的中线BD
27、把ABC的周长分成15和21两部分，求ABC各边的长【分析】本题由题意可知有两种情况，AB+AD15或AB+AD21从而根据等腰三角形的性质及三角形三边关系可求出ABC各边的长【解答】解：BD是等腰ABC的中线，可设ADCDx，则ABAC2x，又知BD将三角形周长分为15和21两部分，可知分为两种情况AB+AD15，即3x15，解得x5，BC21x21516，此时等腰ABC的三边分别为10，10，16；AB+AD21，即3x21，解得x7；此时等腰ABC的三边分别为14，14，8经验证，这两种情况都是成立的ABC各边的长是10，10，16或14，14，8【点评】本题主要考查等腰三角形的性质及三
28、角形三边关系；注意：求出的结果一定要检验时符合三角形三边性质分类讨论是正确解答本题的关键22（8分）（2022秋淮南期末）（1）如图1，有一块直角三角板XYZ放置在ABC上，恰好三角板XYZ的两条直角边XY、XZ分别经过点B、CABC中，A30，则ABC+ACB ，XBC+XCB （2）如图2，ABC的位置不变，改变直角三角板XYZ的位置，使三角板XYZ的两条直角边XY、XZ仍然分别经过B、C，那么ABX+ACX的大小是否变化？若变化，请举例说明；若不变化，请求出ABX+ACX的大小【分析】本题考查的是三角形内角和定理已知A30易求ABC+ACB的度数又因为X为90，所以易求XBC+XCB【解
29、答】解：（1）A30，ABC+ACB150，X90，XBC+XCB90，故答案为：150；90（2）不变化A30，ABC+ACB150，X90，XBC+XCB90，ABX+ACX（ABCXBC）+（ACBXCB）（ABC+ACB）（XBC+XCB）1509060【点评】此题注意运用整体法计算关键是求出ABC+ACB23（9分）（2023春高新区期中）如图，在ABC中，ADBC于D，AE平分BAC（1）若C70，B40，求DAE的度数（2）若CB30，则DAE （3）若CB（CB），求DAE的度数（用含的代数式表示）【分析】（1）根据角平分线的定义和互余进行计算；（2）根据三角形内角和定理和角平
30、分线定义得出DAE的度数等于B与C差的一半解答即可；（3）根据（2）中所得解答即可【解答】解：（1）由已知可得，BAC180407070，CAD20，DAECAECAD352015；（2）B+C+BAC180，BAC180BC，AE平分BAC，BAE=12BAC=12（180BC）90-12（B+C），ADBC，ADE90，而ADEB+BAD，BAD90B，DAEBADBAE（90B）90-12（B+C）=12（CB），CB30，DAE=123015，故答案为：15；（3）CB，DAE=12=12【点评】本题考查了三角形内角和定理，关键是根据三角形内角和是180和三角形外角性质解答24（9分）
31、（2022秋城关区校级期末）如图1，一张三角形ABC纸片，点D，E分别是ABC边上两点研究（1）：如果沿直线DE折叠，使点A落在CE上的点A处，则BDA与A的数量关系是 ；研究（1）：如果折成图2的形状，猜想BDA，CEA和A的数量关系是 ；研究（3）：如果折成图3的形状，猜想BDA，CEA和A的数量关系是什么，并说明理由【分析】研究（1）：翻折问题要在图形是找着相等的量图1中DE为折痕，有ADAA，再利用外角的性质可得结论BDA2A；研究（2）：图2中A与DAE是相等的，再结合四边形的内角和及互补角的性质可得结论BDA+CEA2A；研究（3）：图3中由于折叠A与DAE是相等的，再两次运用三角
32、形外角的性质可得结论【解答】解：（1）BDA与A的数量关系是BDA2A；故答案为：BDA2A；（2）BDA+CEA2A，理由：在四边形ADAE中，A+DAE+ADA+AEA360，A+DAE360ADAAEA，BDA+ADA180，CEA+AEA180，BDA+CEA360ADAAEA，BDA+CEAA+DAE，ADE是由ADE沿直线DE折叠而得，ADAE，BDA+CEA2A；故答案为：BDA+CEA2A；（3）BDACEA2A理由：DA交AC于点F，BDAA+DFA，DFAA+CEA，BDAA+A+CEA，BDACEAA+A，ADE是由ADE沿直线DE折叠而得，ADAE，BDACEA2A【点
33、评】此题考查了三角形内角和定理，注意此类一题多变的题型，基本思路是相同的，主要运用三角形的内角和定理及其推论进行证明25（12分）（2023春天宁区校级期中）在ABC中，BD平分ABC交AC于点D，点E是线段AC上的动点（不与点D重合），过点E作EFBC交射线BD于点F，CEF的角平分线所在直线与射线BD交于点G（1）如图，点E在线段AD上运动若ABC40，C60，则BGE的度数是 ；若A70，则BGE ；探究BGE与A之间的数量关系，并说明理由；（2）若点E在线段DC上运动时，BGE与A之间的数量关系与（1）中的数量关系是否相同？若不同，请直接写出BGE与A之间的数量关系，不需说理【分析】（
34、1）根据角平分线的性质，平行线的性质以及三角形内角和定理即可求解；根据三角形内角和定理先求出ABC+C，再利用角平分线的性质和平行线的性质即可求解；由即可推出数量关系；（2）分为点E在线段CD上和点E在DC的延长线上，分别作出图形，即可求解【解答】解：（1）ABC40，BD平分ABC，CBD20，EFBC，C60，CEFC60，EFGCBD20，EG平分CEF，FEGDEG30，BGEEFG+FEG50；A70，ABC+C180A110，EFBC，CDEF，ABC+DEF110，BD平分ABC，EG平分CEF，CBD=12ABC，FEG=12DEF，CBD+FEG=12ABC+12DEF=12
35、11055，EFBC，EFGCBD，EFG+FEG55，BGEEFG+FEG55；ABC+C180A，EFBC，CDEF，ABC+DEF180A，BD平分ABC，EG平分CEF，CBD=12ABC，FEG=12DEF，CBD+FEG=12ABC+12DEF=12（180A）90-12A，EFBC，EFGCBD，EFG+FEG90-12A，BGEEFG+FEG90-12A；故答案为：50，55；（2）当点E在线段CD上，若GE交BC于点H，由（1）知：1=12ABC，2=12CEF，EFBC，CEF180C，23=12（180C），1+A+BDA180，3+BGE+EDG180，且BDAEDG，3+BGE1+A，BGE1+A3，即BGE=12ABC+A-12（180C）=12ABC+A90+12C=12（ABC+C）+A90=12（180A）+A9090-12A+A90=12A；【点评】本题考查三角形内角和定理，平行线的性质，角平分线的性质，解题的关键是掌握分类讨论的思想，难点在于（2）需要考虑点E在线段CD上和点E在DC的延长线上
